深水区地震资料处理变参数振幅恢复技术
陈殿远 刘仕友 孙万元
中海石油(中国)有限公司湛江分公司
0 引言
处理中的变参数振幅补偿技术,有效地解决了浅水—坡折带—深水区域资料的保幅性问题。
现今油气勘探的重点领域逐渐转向深水区油气藏,从海洋地震资料中可以发现,深水区的地震资料存在诸多问题[1-3]。目前,大多数技术手段都是假设地下介质近似水平层状,未考虑海水的物理特征以及大陆坡折带地区的实际情况。在浅水地震资料处理中,往往可忽略海水的声学性质,然而在深水地震勘探中,海水深度介于1 000~3 000 m,海水的声学性质也明显不同于岩石,地震波在海水中的传播速度(以下简称海水速度)具有明显的分层性[4-6]。宋洋等[7]提出利用地震剖面获取海水层温度、盐度、密度等物理参数,证明海水非单一均匀介质。韩复兴等[8-9]从影响海水速度变化的主要因素(海水温度、盐度和深度)的经验公式出发,建立海水速度模型,分析讨论了海水速度变化对地震波走时、射线路径及振幅的影响。Berryhill[10]首次针对崎岖海底提出波动方程解决思路,邓盾等[11-12]从叠前深度域保幅偏移算法、双方位地震资料联合成像两方面对崎岖海底成像进行研究。
另一方面,海水不是理想的无损耗介质,当声波在海水中传播时,随着距离的增加,声强将逐渐减弱。很多学者都对海底沉积物的吸收性质开展了理论研究和实际测量[13-19],但是,目前还没有学者针对地震波在海水中振幅的衰减规律开展研究。Bevc等[20-23]采用叠前深度域偏移方法来保证崎岖海底成像并以此达到振幅补偿的目的,但其崎岖海底起伏范围均为几百米内,未达到深水勘探的1 000~3 000 m。Claerbout等[24-25]对海洋地震资料进行了衰减补偿,但也未考虑不同介质的振幅衰减差异问题。
为了解决上述问题,笔者采用深水机器人、海水实验室测量及深水VSP等多种方法定量测量了地震波在海水中的速度,明确了其分层特征,建立了分层模型,提出了在深水区特别是深水坡折带地震资料
1 海水与海底沉积物声学性质
1.1 水下机器人实测
2013年12月,在南海北部琼东南盆地深水区首次利用水下机器人对海水进行了多次速度测量,最大测量水深1 500 m,并开展了系统的研究工作,得到如下认识:①深水区海水的速度具有明显的三层结构(图1-a),浅层(80 m以上)海水速度变化较小;②深度介于100~1 200 m,由于海水温度逐渐降低(图1-c),地震波在海水中的速度快速降低后逐渐降低到1 485 m/s;③1 200 m以下,海水温度不再明显降低,海水盐度逐步控制了海水速度(图1-b),盐度升高,海水速度逐渐升高。海水声学性质受多方面影响,具有明显的分层成带现象。
1.2 实验室测定
实验室测定海洋参数是海洋油气资源研究的重要手段。笔者采用流体声波测试仪测试不同静水压力下海水和海底沉积物的声学性质,其承压能力高达60 MPa,最高承受温度为180 ℃。声波速度采用透射法测量原理,纵波发射纵波接收,获得如表1所示参数。实验室成像结果显示(图1-d),虽然数值与海洋实测参数有所不同,但得到的规律与水下机器人的测量结果基本相同:①海水速度在水深0~800 m区域随深度增加快速递减;②水深800~1 500 m,海水速度随深度增加而缓慢递减;水深1 500~2 000 m,海水速度随深度增加快速递减;③水深大于2 000 m,海水速度则随深度增加而快速递增。淤泥速度在0~500 m水深区域随水深增加而快速递减,同时小于海水速度;在大于500 m水深区域,淤泥速度基本无变化,而在水深500~1 700 m,淤泥速度低于海水速度,超过1 700 m,淤泥速度则大于海水速度。
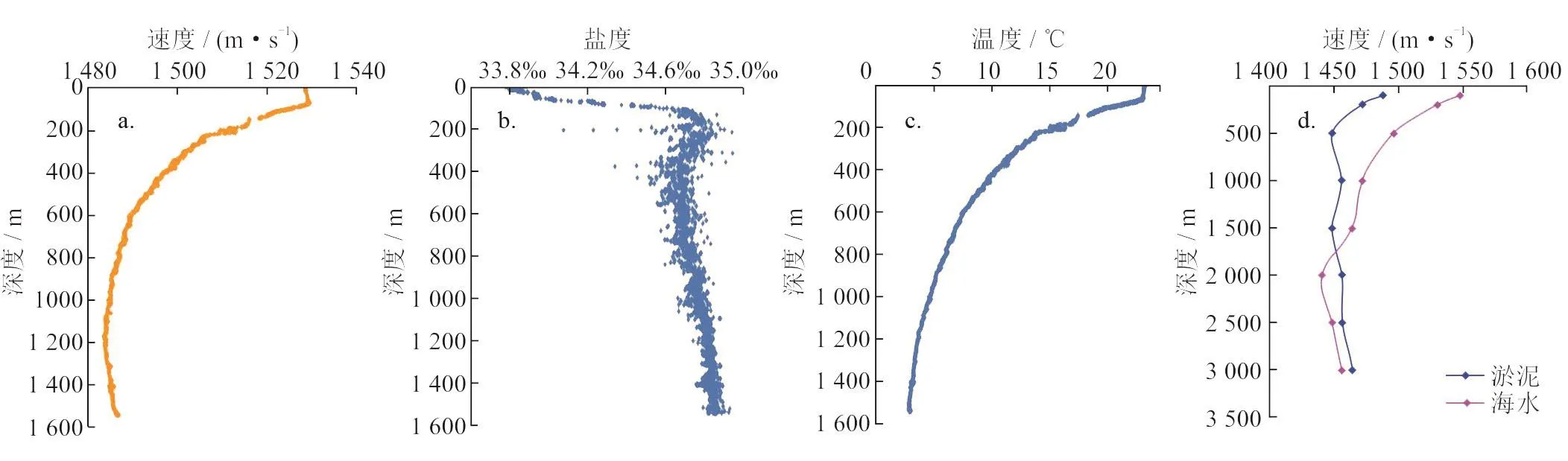
图1 陵水深水区海水参数实测与实验室测量结果图
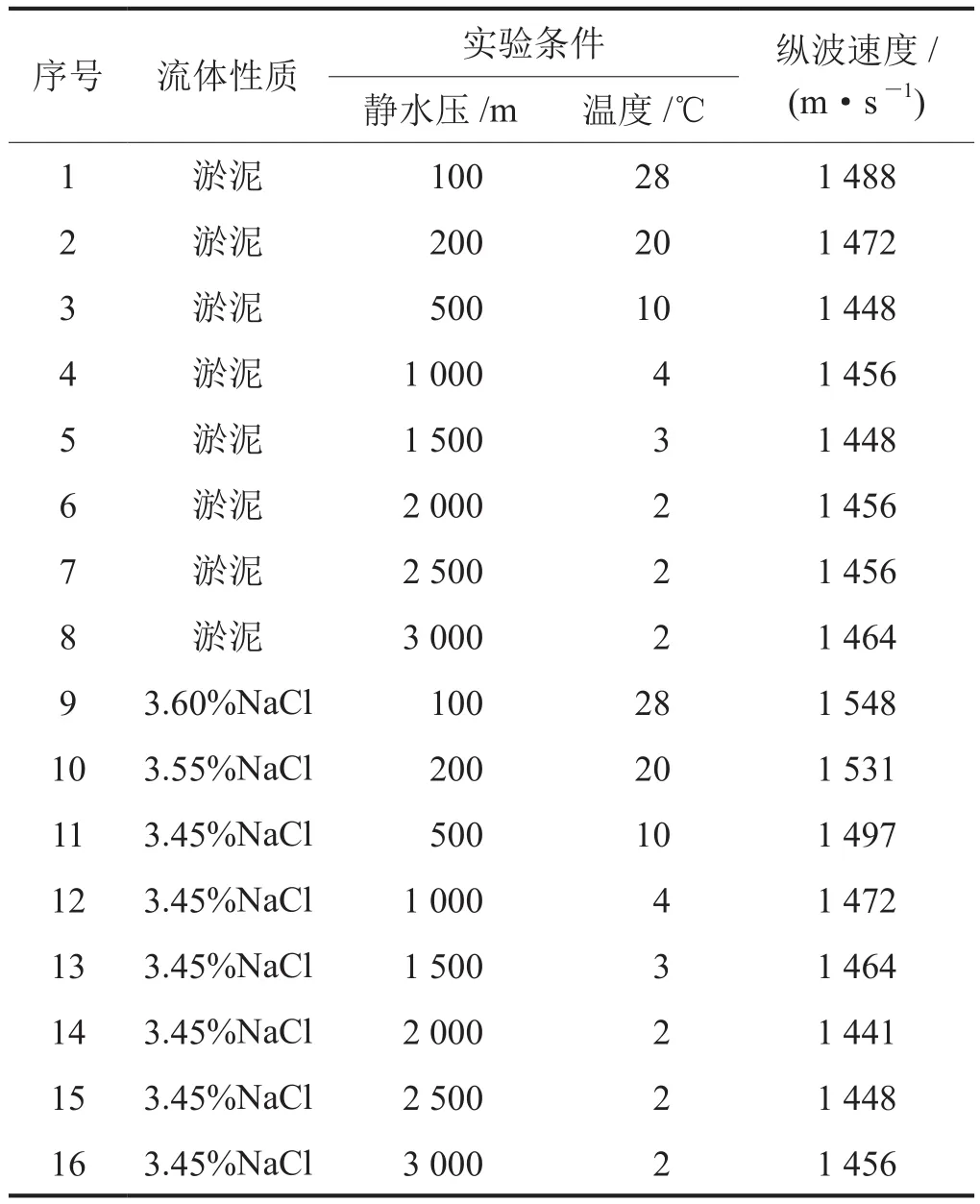
表1 实验室测得的海水与海底沉积物声学性质表
1.3 海水与地层衰减规律差异
为了更精确地测量地震波在海水中垂向传播的球面扩散规律,定量研究在海水和地层两种介质中地震波衰减规律的差异。除了实验测定外,还在南海深水区开展了VSP测量。通过测量不同深度地震波的振幅,就可以直接拟合出其振幅的衰减规律。测量方法:将VSP测量仪器直接放入海水中,其依靠自身重力直接沉入水下。测量过程:仪器在进入海平面时对零,每隔50 m放炮,测量完毕时在海平面再次对零。通过叠加,噪声得到了有效压制,有效信息得到了增强。提取了每一个深度点的地震子波的均方根振幅,用指数函数A=aRb进行拟合,其中A表示相对振幅,a、b表示衰减系数,R表示传播距离。当拟合振幅衰减函数A=1.0R-0.705,即a=1.0、b=-0.705(图2),而以上述水体声学物理特征结果正演的振幅衰减函数则为A=1.0R-0.66。
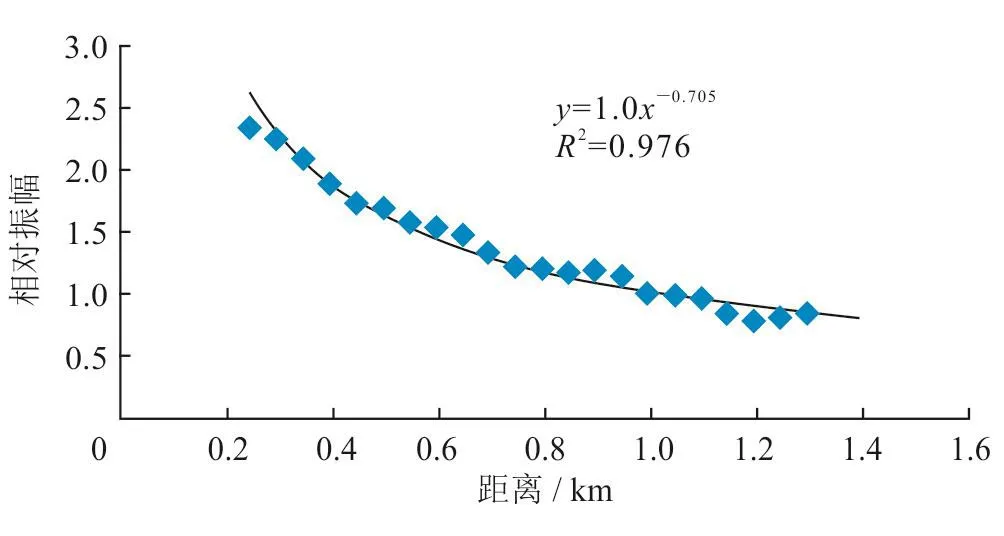
图2 海水中地震波传播距离和振幅的关系图
海水可近似认为是均匀介质,经典的球面扩散理论预测的结果是A=1.0R-0.1。这与实际测量的结果并不吻合,表明海水的振幅衰减规律比球面扩散理论的预计要弱得多。
笔者从南海北部多个盆地挑选多口已钻井的VSP资料进行处理和分析(表2中1井、2井、3井)。在波场分离的基础上,提出了直达下行波的子波振幅,并对子波振幅进行归一化处理,还去除了水深变化的因素,仅考虑在地层中传播的振幅衰减问题。用指数函数A=aRb拟合测量数据,结果表明:在地层中衰减系数b介于1.8~2.3,而在海水中衰减系数b介于0.60~0.75(表2)。从表2中可以看出,海水和地层的振幅衰减规律存在巨大的差别,地震波传播相同的距离,在海水中的振幅衰减比地层要弱很多。这个差异是目前深水地震振幅恢复技术没有考虑的因素。
通常地层的振幅衰减规律变化不大,通过时变振幅恢复等办法就可以解决不同地层的振幅衰减差异问题,但时变振幅恢复方法在大陆坡折带地区的应用效果并不理想,主要原因在于海水和地层的振幅衰减规律差异大且突变。
从理论上讲,单炮可以作为一个点震源产生的球面波场。经典的球面扩散理论认为:对于没有衰减、均匀、水平层状介质而言,地震波的能量衰减正比于1/r2(r为球面半径),振幅随传播半径的增大而减弱。一般而言,地震纵波速度随深度增加,使地震波进一步发散,振幅衰减也随距离的增加而加快。

表2 地震波的振幅衰减随传播距离的规律表
在地震波实际传播过程中,振幅衰减机制却是十分复杂的问题。地震波振幅衰减因素大体上可以分为5个因素[17]。笔者列举和对比了这些因素在海水和地层两种介质中的差异(表3)。不难得到结论,在海水和地层两种介质中,地震波振幅衰减的因素存在差异。

表3 海水、地层两种介质中地震波振幅的衰减因素差异表
2 深水地震资料解释保真处理技术
2.1 变海水速度对深水资料深度偏移成像的影响
速度建模是深度偏移中非常关键的一步,速度模型的准确与否直接关系到深度偏移成像的好坏。PSDM是解决复杂地质体成像的有力工具,其成像的质量主要取决于所用的速度—深度模型的精度。在浅水区,海水深度横向变化小,海水速度相对稳定,对下伏地层成像的影响很小,可以忽略。而当地震工区跨越浅水、坡折带、深水地区时,海水深度的横向快速变化导致速度场剧烈横向变化,严重违背了叠前深度偏移方法对速度场的基本假设,成为影响地震偏移成像的关键因素。
海水速度随着海底深度的变化而变化,在进行叠前深度偏移处理时,通常情况下海水速度给定常数值,若海底比较平坦,则对后期成像基本无影响。但如果海底是崎岖变化的,水深变化比较大的情况下,会对下伏地层造成很大的影响,必须考虑海水速度随水深的变化。对模型数据进行试算,结果表明:在崎岖海底条件下,如果不考虑这种变化,直接用常速充填,会对下伏地层造成假构造。如图3所示,图3-b为在常数海水速度下,水平界面出现假的背斜构造特征(图3-d圆圈部分),图3-a将海水的分层特征信息转化成平均层速度模型,其水平界面归位准确。
将层状海水速度应用到实际资料的处理中,从图3中可以看出,相较于常数海水速度偏移剖面(图3-f),层状海水速度偏移效果(图3-e)具有同相轴更为连续、信噪比更高的伏点,提高了整体成像分辨率与成像精度。
2.2 不同海水深度衰减对地震真振幅恢复的影响
在地震剖面上,地震响应的可信度取决于资料处理的保真度。在岩性勘探中,地震资料保真处理是关键[26-28]。只有最大限度将储层物性的地震响应真实反映到地震剖面上,才能有效利用地震数据识别岩性储层。保真地震资料处理主要包含:保持相对振幅关系、保护有效频带、保护地震低频、保持地震相位。其中,保持相对振幅关系占有最重要的地位,是保真地震资料处理的核心。因此,地震资料的振幅恢复不仅是地震资料处理的重要课题,也直接影响了烃类检测、储层研究、声波阻抗反演等很多课题。
2.2.1 球面扩散补偿方法
依据射线理论Ursin等[29]给出的水平层状、弹性介质下偏移距相关的球面扩散公式,并用泰勒级数展开。
在垂直入射时,地震波的振幅恢复函数D可以表示为:

其中
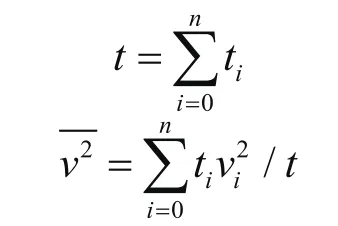
式中t表示双程旅行时;表示速度平方的平均值;ti、vi分别表示第i层的时间和速度。
球面扩散恢复增益函数定义为:

式中v0表示对应时刻t0时的速度值。
如果不是零偏移距地震数据,对于水平层状介质其球面扩散的公式为:

其中

式中X表示偏移距;θi表示第i层的入射角;di表示第i层的厚度。

图3 变海水速度对深度偏移成像影响图
在实际中,常用的公式还有Claerbout[24]提出的根据时间的恢复函数:

Claerbout[24]推荐a的取值为2。通常a的取值范围介于1.6~2.2。
2.2.2 变参数振幅补偿方法
笔者提出了变参数振幅补偿方法,该方法充分考虑不同介质具有不同的振幅衰减规律。具体做法为:沿地震波传播路径将地下介质分成各小段,分别计算每一小段的旅行时间和补偿系数,总的补偿系数D就是各小段补偿的乘积。
通常地,假设地下介质是水平层状介质。把地下分为n层,每一个小层的厚度分别记做d1,d2, …,dn。地震波在每一小层的传播路径分别是r1,r2, …,rn。在垂直入射时,得到的振幅和传播距离的关系:

其中
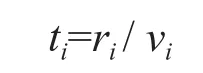
式中a1,a2, …,an表示每一段小层的补偿系数。由于每一小层的补偿系数是不一样的,就可以妥善处理不同介质振幅衰减规律不一致的情况。
引入补偿系数ai对每一个小层进行精细补偿,并可控制海水和地层补偿函数的界面。对于偏移距域的水平层状介质,可以得到:
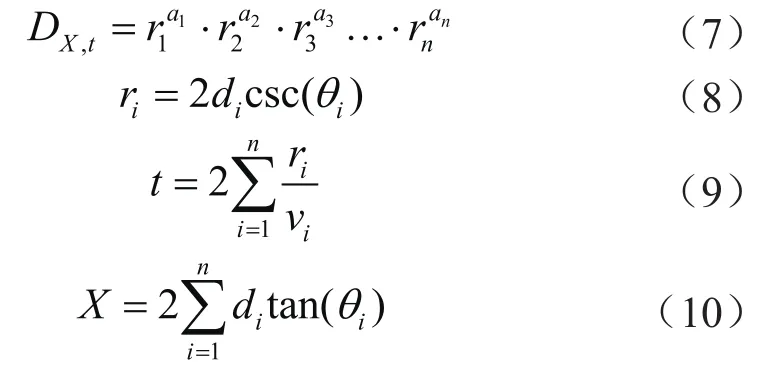
变参数补偿主要针对水深变化大的区域,在相同旅行时情况下,其在海水和地层中的传播距离并不一致,能量衰减和补偿也不一样,如图4中的路径1和路径2就具有相同的旅行时。

路径1、2的补偿系数分别为:
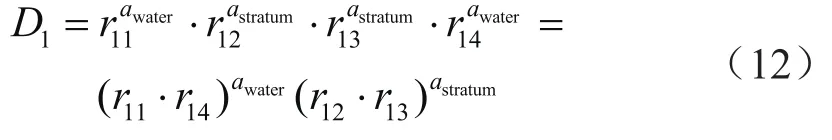
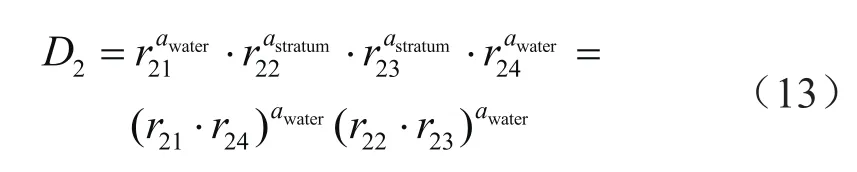
由此即可有效消除因海水与地层具有不同衰减系数而带来的地震资料保幅不一致的问题。
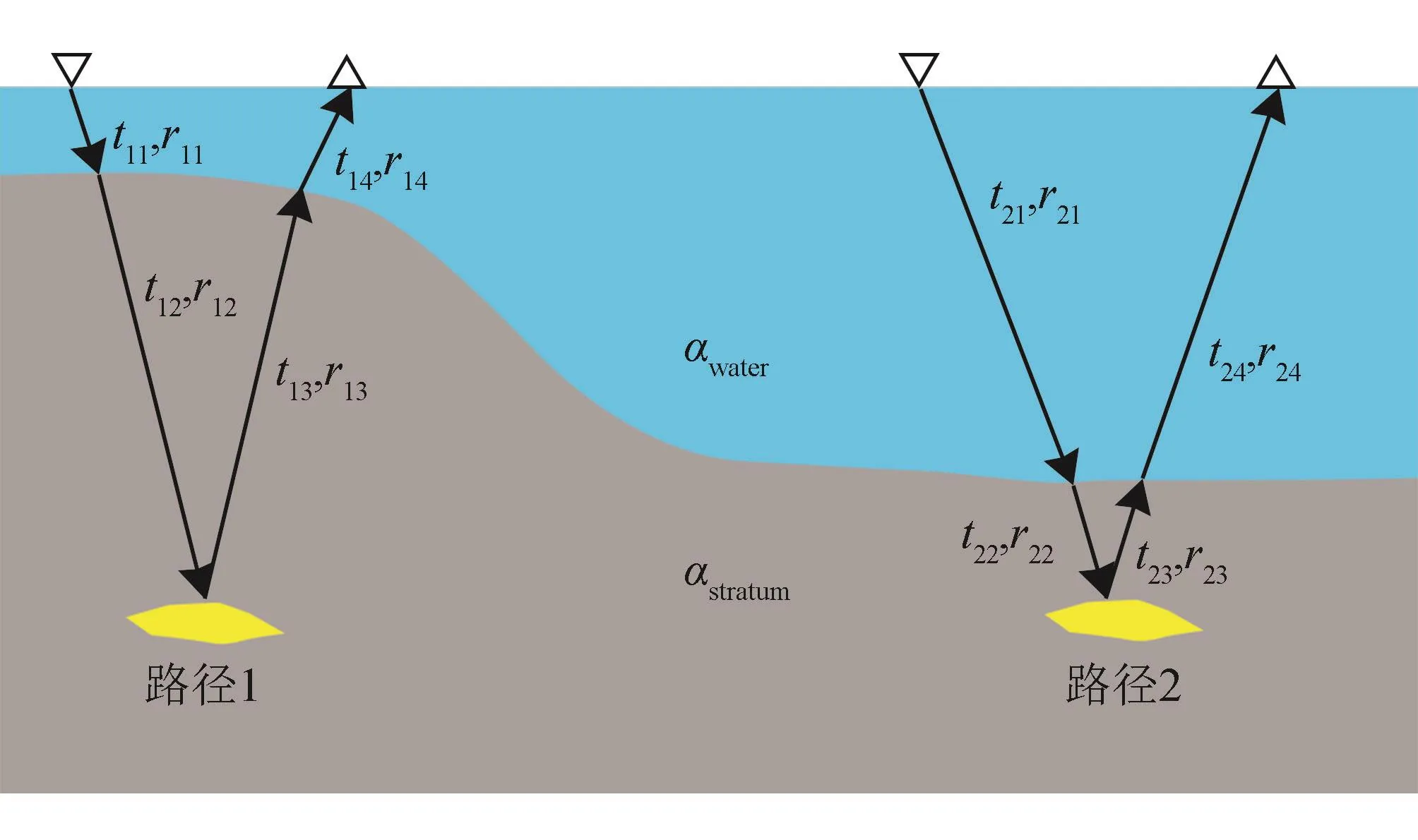
图4 深浅水等时路径补偿差异示意图
2.2.3 琼东南坡折带实际地震资料变参数振幅补偿
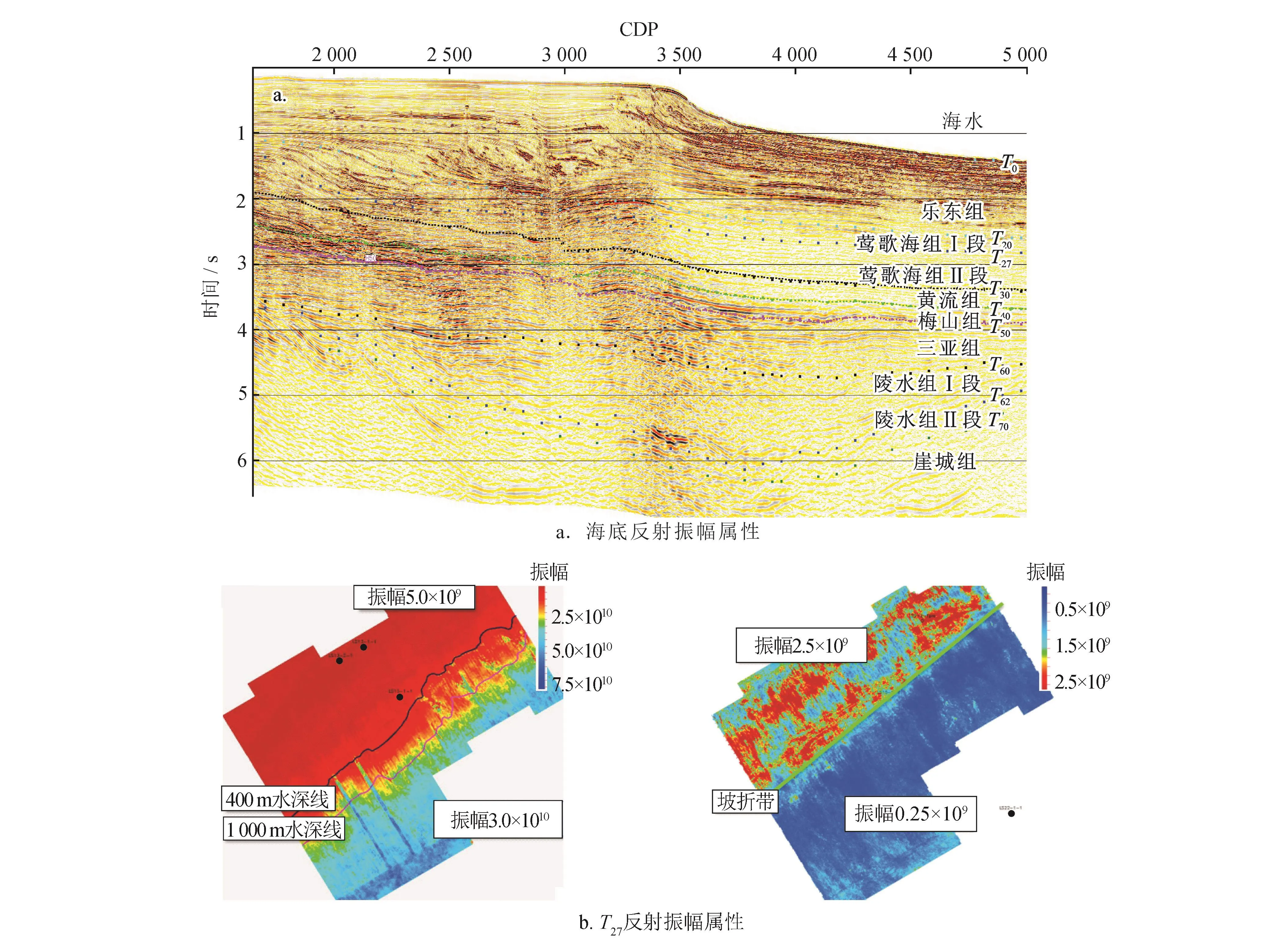
图5 坡折带处地震资料图
本文处理的地震资料来自南海北部大陆边缘的琼东南盆地,其海水深度介于150~3 000 m。从三维工区截取一条主测线可以看出(图5-a),在纯波剖面中,振幅以坡折带为界,深浅水存在明显差异:深水的海底反射明显强于浅水;从T20~T50,浅水反射明显强于深水反射。从纯波剖面中提出了海底、T27两层反射的振幅属性更能说明这个问题(图5-b),从图中可以看出,分为浅水振幅属性和深水振幅属性两个区域,两个区域的振幅属性完全不一样,并且与坡折带高度吻合。
图6是采用不同振幅恢复方法得到的叠加剖面(沿海底拉平)。传统补偿方法的结果(图6-b),浅水振幅明显强于深水振幅,坡折带两侧相同地层的振幅无法对比。变参数振幅补偿方法的结果(图6-c),深水和浅水的振幅在横向上和垂向上更加均衡;同一反射层位可以从浅水区连续追踪到深水区,振幅是连续、可靠的。由于浅水海底沉积物的反射系数大于深水沉积物的反射系数,所以浅水海底的反射应该强于深水海底反射。传统方法补偿后,浅水海底反射振幅弱于深水海底反射振幅,这主要是由于Newman补偿函数带来的过补偿问题。在变参数振幅补偿结果中,浅水区的海底反射是一个强反射,强于深水海底反射。所以,变参数振幅补偿结果才是真实地下反射系数的表达。在CRP道集中,传统方法补偿结果在远偏移距出现了强振幅异常问题(图7-a)。变参数振幅补偿的结果在偏移距方向的振幅均衡,AVO属性更加合理,避免了远偏移距的强振幅异常现象(图7-b)。

图7 不同水深的CRP道集补偿效果对比图
3 深水区高保幅地震资料的应用
深水峡谷水道LSX10井区靠近峡谷水道壁,侧封条件优越,具有较大的油气勘探潜力,准确评价其物性与含气性至关重要。常规AVO分析结果如图8所示,从2个设计井点的AVO分析可以看出(图8),该目标的G(梯度)属性较小,振幅随偏移距的微弱变化呈Ⅲ—Ⅳ类变化,从砂体顶界面原始AVO特征(图9-a)和PXG属性(图9-c)可以看出,该砂体的AVO类型具有多变性。根据从变振幅恢复后AVO交汇图(图9-b)得出的含气性指示因子(图9-d),预测含气边界清晰、含气范围可靠;同时可以得到孔隙度指示因子(图9-e),预测储层物性好,砂体孔隙度预测为30%。在2020年部署LSX10探井,实钻结果显示钻遇厚套气层,孔隙度为32.1%,渗透率为861 mD,证实了海水声学物理特征研究及基于其上的变参数振幅补偿技术对于含气性及孔隙度预测的有效性。
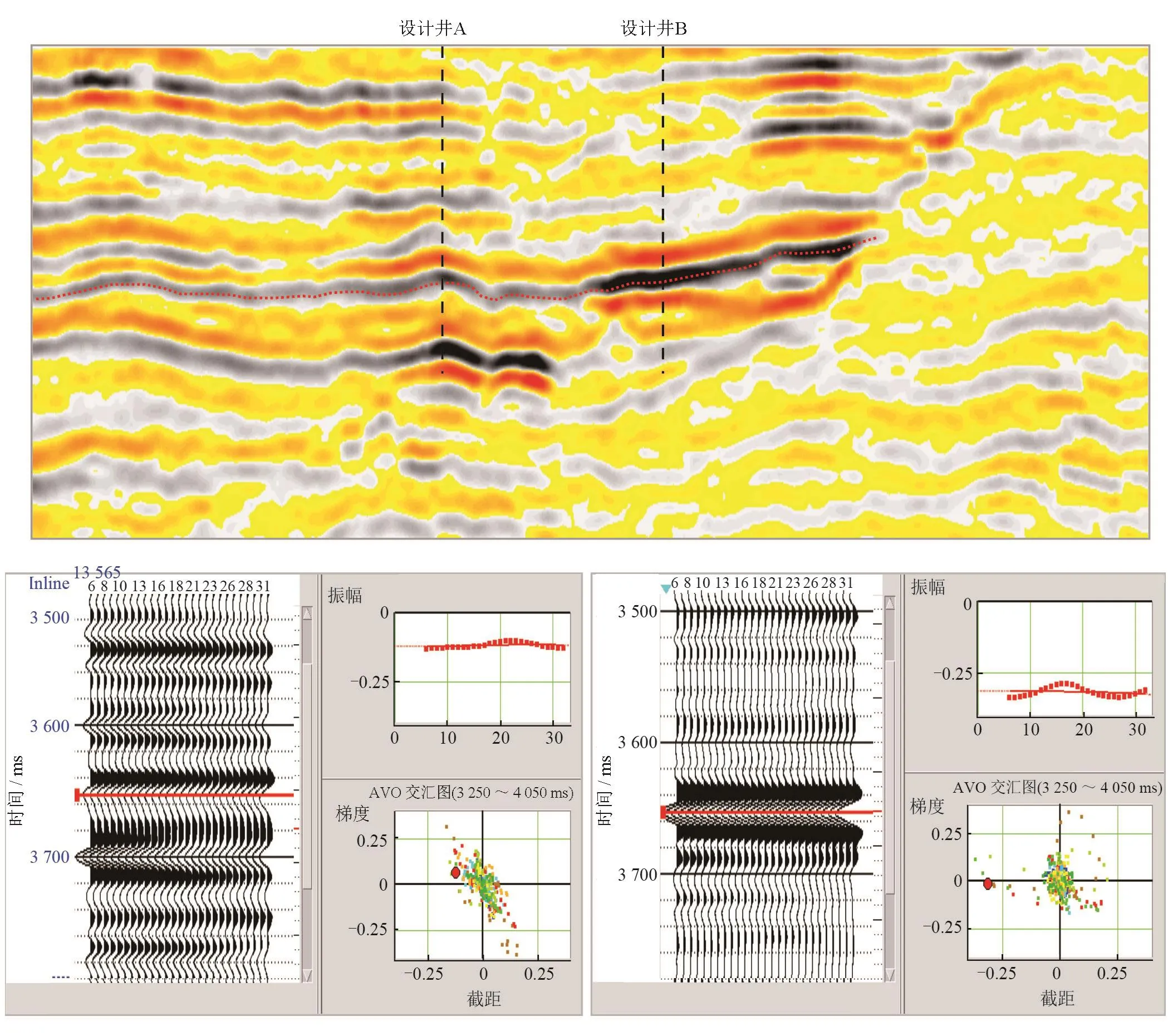
图8 典型地震剖面及AVO变化规律特征图
4 结论与建议
1)基于实际野外测量数据与实验室测量数据融合,明晰海水与海底沉积物声学特性随水深变化呈现明显分层性,同时考虑海水与地层衰减差异,针对水深变化区域,提出了变参数地震振幅恢复技术,有效解决了浅水—坡折带—深水区域资料保幅性问题。
2)在琼东南实际资料处理中,该方法补偿的振幅更加均衡,同一反射地层可以连续追踪;在偏移距方向,近、中、远偏移距的地震振幅变化更加合理。保幅的地震信息为后续的储层预测和烃检奠定了重要的资料基础。本研究成果在深水以及超深水等水深变化剧烈区带勘探中具有重要的应用价值。
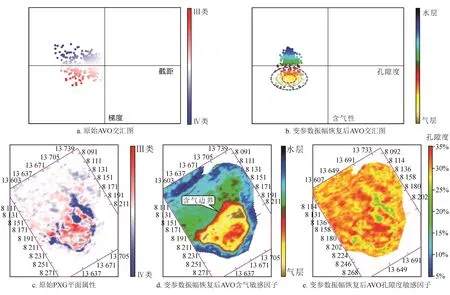
图9 砂体顶界面AVO特征图

