基于Matlab的电气量波形与相量同步显示示波器开发与应用

李 伟，江献玉，周喜军，刘 仁，田 侃，杨 柳，徐三敏，赵晓琳

（国网新源控股有限公司技术中心，北京市 100161）

0 引言

在电力系统研究中，时域波形和相量图都是常用的分析工具，经常需要将两者结合应用。故障录波器可以显示时域波形，并同步显示指定时刻的相量图，但故障录波器无法应用于Matlab环境。Matlab的图形化仿真工具包Simulink的示波器（Scope）功能强大，但只能显示时域波形，没有谐波分析功能。在Simulink环境下用相量法（Phasor）进行仿真时，可直接在示波器中观察各种电气量的相量值，但示波器显示的只是分别反映相量幅值和相角的两条水平线，不能直观地显示出与相量对应的矢量图，而且采用相量法分析时无法同步显示时域波形。因此，目前尚无手段能在Matlab环境中对时域波形与相量进行同步显示，这对继电保护研究工作造成了一定的不便。

针对此问题，本文研究开发了基于Matlab的时域波形和相量图同步显示示波器软件，任意指定某一时刻，软件将立即对该时刻的电气量进行计算，显示相量位置，并给出该时刻的基波序分量和谐波分量计算结果，极大地方便了研究分析。

1 开发同步显示示波器的关键技术

要实现从电力系统稳态或暂态电气量波形中正确地算出基波和谐波相量，需要解决一系列的问题，这里主要包括：如何提取相量，如何克服故障暂态电流所包含的衰减直流分量，如何应对Yd11接线变压器两侧电流相位差，以及Matlab界面开发等。

1.1 傅氏算法计算相量

实现同步显示示波器的关键是计算出时域波形任意时刻基波序分量和谐波分量，可采用傅氏（傅里叶）算法来完成[1，2]。根据所需数据窗长度的不同，傅氏算法可分为全周和半周傅氏算法，两者在电力系统信号处理中都有广泛应用。本文的示波器采用全周傅氏算法。

设待分析的电流信号为i(t)，该信号一般为周期信号，可将其分解为傅氏级数如下：

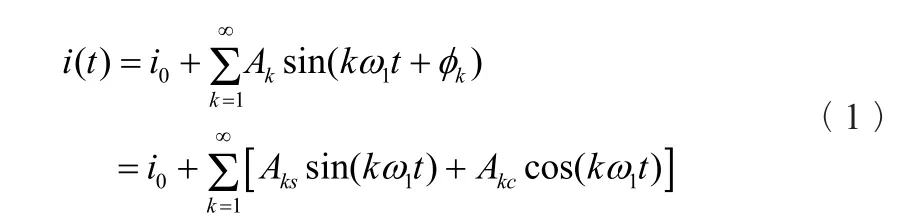
式中i0——i(t)含有的直流分量；

ω1——基波分量的角频率，rad/s；

k、Ak、φk——第k次谐波相量的幅值和相角；

Aks、Akc——第k次谐波的正弦系数和余弦系数。

因此，第k次谐波相量的幅值和相角可以计算如下：

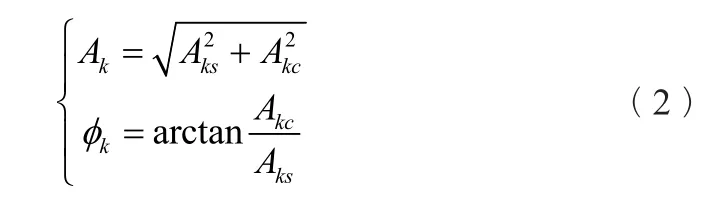
将波形按每周波N点采样进行离散化采样，根据傅氏算法的结论，可知正弦系数Aks和余弦系数Akc可按如下公式计算：

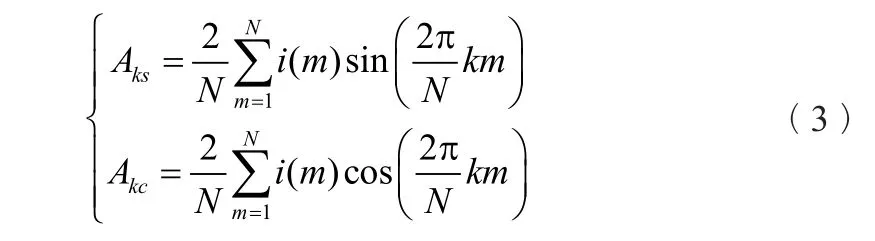
式中m——采样点编号，从1到N；

i(m)——第m个采样点。

因此，在某个指定的时刻，只要采集该时刻及其此前的全部N个采样点，即可根据式（3）和式（2）计算出基波和任意第k次谐波的相量幅值和相角。

1.2 滤除衰减直流分量的影响

电力系统的短路电流除了有基波及各次谐波分量之外，还含有衰减直流分量[2]，因此故障电流i（t）改写为如下式所示：

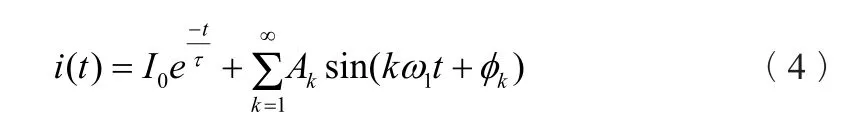
式中I0、τ——衰减直流分量的初始值和时间常数。

若不对衰减直流分量进行处理，直接利用i(t)的采样值进行傅氏计算，将会造成较大的误差，当τ≈0.44时的误差可达15%，这对于继电保护装置来说是不可接受的[3，4]。因此，必须采取措施滤除衰减直流分量。

目前主要采用两种方法滤除衰减直流分量，其一是直接用采样值进行傅氏计算然后再进行修正，其二是先对采样值利用差分滤波器进行处理，然后才进行傅氏计算。差分滤波器原理简单，计算量也小，本文的示波器采取第二种方法。因为差分滤波器总能滤除直流分量，所以选择对采样值数据量要求最少的一阶差分滤波器。

设采样值序列为i(n)，按下式进行一阶差分计算：

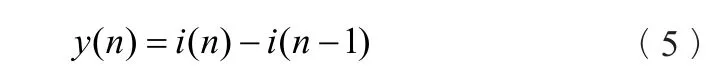
因为采样时间很短，可以近似认为在相邻两个采样时刻的衰减直流变化不大，因此计算结果中就滤除了衰减直流。

但也正是因为差分，即使i(n)是纯交流量，差分结果y(n)也必定和i(n)不同，导致y(n)和i(n)的傅氏计算结果不同，因此需要根据差分滤波器的响应特性进行修正。对式（5）进行z变换，求得转移函数为：

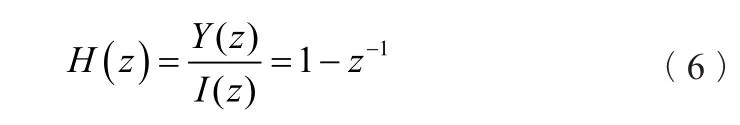
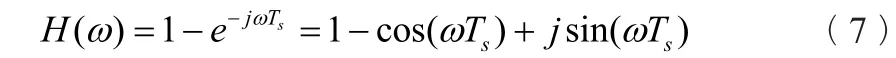
式中ω——信号所含基波或谐波的角频率，ω=kω1；

Ts——采样时间间隔，

据此进一步得到一阶差分滤波器的幅频特性和相频特性如下：

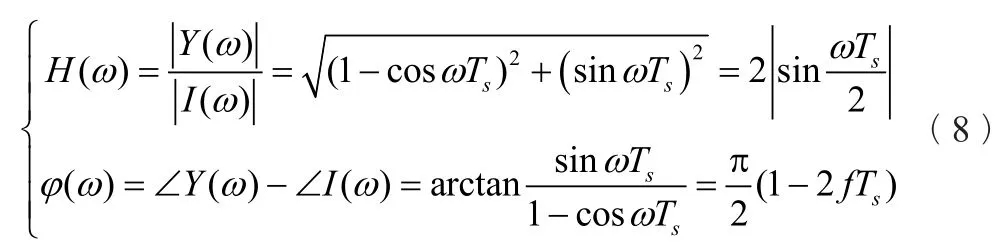
式中f——电流所含基波或谐波的频率f=kf1，f1为基波频率。

根据式（8）可得一阶差分滤波后的幅值修正和相位修正公式如下：

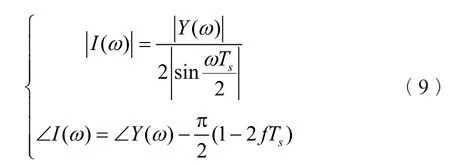
现以一个算例来具体说明差分滤除衰减直流和恢复出原始的纯交流分量。设待分析电流仅含有衰减直流分量和基波分量，基波在0s、0.02s和0.04s时的相量为1∠0°，直流的衰减时间常数为0.07s，即i（t）表达式如下：

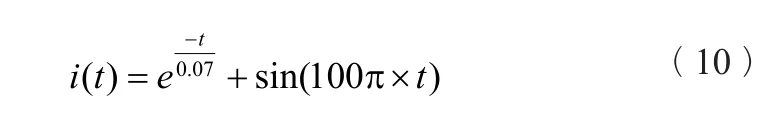
设每基波周期20ms采样20点，Ts=1ms，N=20。在matlab中作出该电流的衰减直流、交流及合成电流，分别如图1（a）、图1（b）、图1（c）所示。图1的各子图横轴坐标均为时间t，单位为s。

对i（t）按式（5）进行差分，结果波形如图1（d）所示，可见差分结果不含直流分量，但幅值和相位都与待分析电流所含的交流分量有较大不同。

在式（10）中代入ω=100π，Ts=1ms，得幅值修正系数为0.3129，相位修正值81°，将差分结果按式（9）进行修正，依次得到图1（e）和图1（f）所示的波形。在进行相位修正时，因每个采样周期对应相移360/N=360/20=18°，所以相位修正值81°对应于4.5个采样点，取整为4个采样点，即将幅值修正后的波形整体向右移动4个采样点，得到图1（f），与图1（b）波形非常近似。

对图1（f）波形进行傅氏计算，得0.04s时的相量为0.9972∠9.044°。若将图1（e）的波形整体向右移动5个采样点，算得相量为 0.9972∠-9.0076°。因此，修正后波形的相量幅值得到几乎精确的恢复，但相角仍有较大偏差，该偏差是由于相位修正角度对应到采样点时的舍入误差导致的。因此，本文后续改为对图1（d）差分结果进行傅氏计算，然后对相量进行幅值和相位修正，从而避免这种舍入误差带来的问题。

1.3 Yd11接线变压器线电流的相位和幅值调整

图1 一阶差分滤除衰减直流分量Figure 1 Example： First order differential filter to remove decaying DC component

对于接线组别为Yd11的变压器，其两侧电流相位差30°，不便于直接观察两侧电流的关系，有必要进行相应调整，这也是变压器差动保护中必有的一个信号处理过程[5]。在微机保护中，变压器各侧电流互感器（简称“TA”）二次侧一般都按Y接线，由软件进行相位和幅值调整[6]。

变压器两侧线电流相量如图2所示。

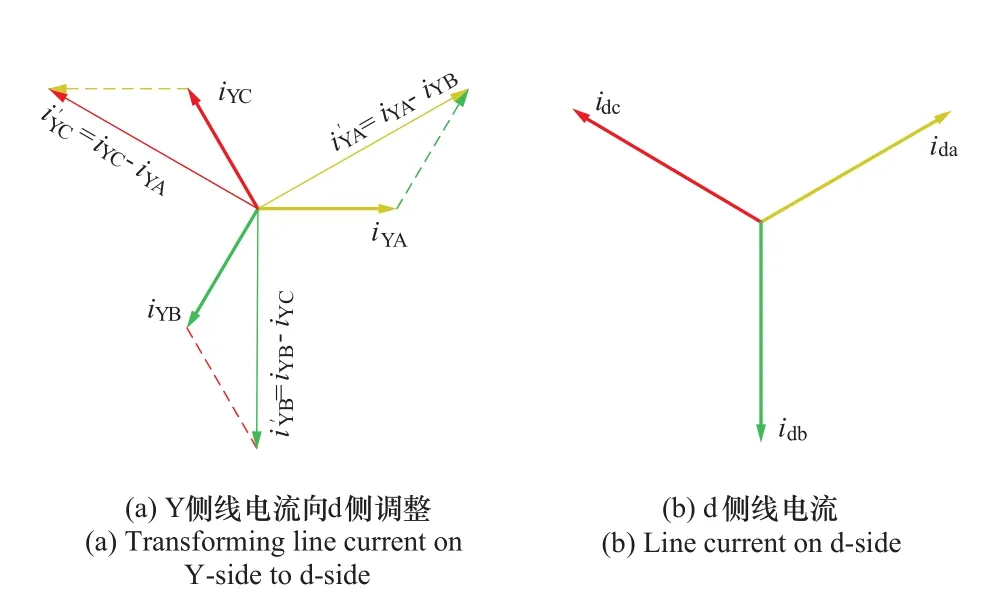
图2 Yd11接线变压器两侧的线电流相量Figure 2 Current phasors on both sides of transformer with Yd11connection

设Y侧TA二次三相电流的采样值为iYA、iYB、iYC，按式（11）向d侧调整。

从图2可知，进行以上调整后的Y侧电流与d侧同相位，但电流幅值将扩大倍，因此将的大小除以，即可抵消相量加减运算带来的幅值放大。将d侧电流向Y侧调整的方法类似。

由于变压器两侧额定电流不相等，以及两侧TA变比不等，导致两侧电流幅值不同，必须进行幅值调整。幅值调整的基本原理是：设Y侧和d侧幅值调整系数分别为KY和Kd，则进行幅值调整后，应满足如下关系式：

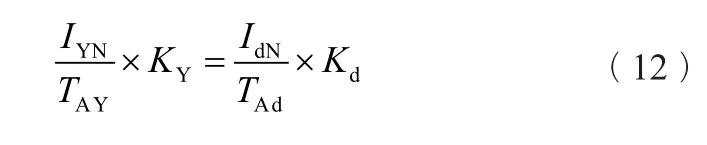
式中IYN、IdN——Y侧和d侧线电流额定值；

TAY、TAd——Y侧和d侧TA变比。

选定按某侧进行调整时，取该侧调整系数为1，计算出另一侧调整系数。

1.4 程序开发要点

1.4.1 程序总体流程

程序完成界面初始化后，等待用户操作。程序从界面上获取要分析的时刻，然后对每一个通道的三相电量依次进行Y/d幅值调整和相位调整、差分滤波、傅氏计算（包括基波和谐波），然后根据三相基波相量算出正序、负序和零序相量，最后根据计算结果修改界面上的相关对象。

为便于同时观察两个电气量，比如差动保护、电压闭锁电流保护等，界面上设置了两个通道，每通道用于一组三相电气量。此外，程序还开发了若干便捷操作，比如隐藏或显示某相曲线从而简化界面、当前时刻的纵向指示线等。

1.4.2 采样点号是程序的关键

本程序需要提取当前采样时刻及此前一周波内的采样值，因此当前时刻所对应的采样点号是联系多个子程序及界面相关元素的关键。

本程序提供了多种途径修改当前采样点，包括：直接指定采样点号，直接指定采样时刻，当前采样点的下一点、当前采样点的上一点、直接在某个通道的时域波形上单击鼠标，这些操作都会导致立刻更新当前采样点并保存，然后进行该时刻的相关计算。

1.4.3 通过结构体handles传递对象句柄和变量

Matlab界面编辑环境guide创建并管理一个名为handles的结构体，该结构体包含有界面上所有对象的句柄值[7]。因此，将handles作为实参传入到各个相关子程序，即可在任一个子程序内操作界面上的任何对象[8]。

本程序还利用handles这一特点来存放需要在多处使用的变量，例如当前采样点号的变量nNow。以界面按钮“下一个采样点”为例，在其回调函数中编写如下语句：

handles.nNow=nNew

将会在handles中新建一个域nNow，将新采样点号nNew存入到该域中，在其他子程序中通过handles.nNow即可获知当前采样点号。

2 同步显示示波器的应用

本文以某抽水蓄能电站（以下简称“抽蓄电站”）主变压器为研究对象，以两个例子说明同步显示示波器在继电保护分析中的应用。

2.1 变压器保护仿真实验系统

该抽水蓄能电站主变压器的主要参数如下：额定容量Sn=360MVA，YNd11接线组，额定电压525/18kV，额定电流395.9/11547A，高压侧TA变比为1250/1A，低压侧TA变比为15000/1A。

为抓住研究重点，设计该实验系统的模型为无穷大电源经主变对负荷供电的简化系统，如图3所示。通过设置主变压器两侧断路器QF1和QF2控制主变压器的投切，设置故障发生器Internal（模拟保护区内短路）和External（模拟保护区外短路），可在主变压器保护区内和区外制造各种相间短路故障。

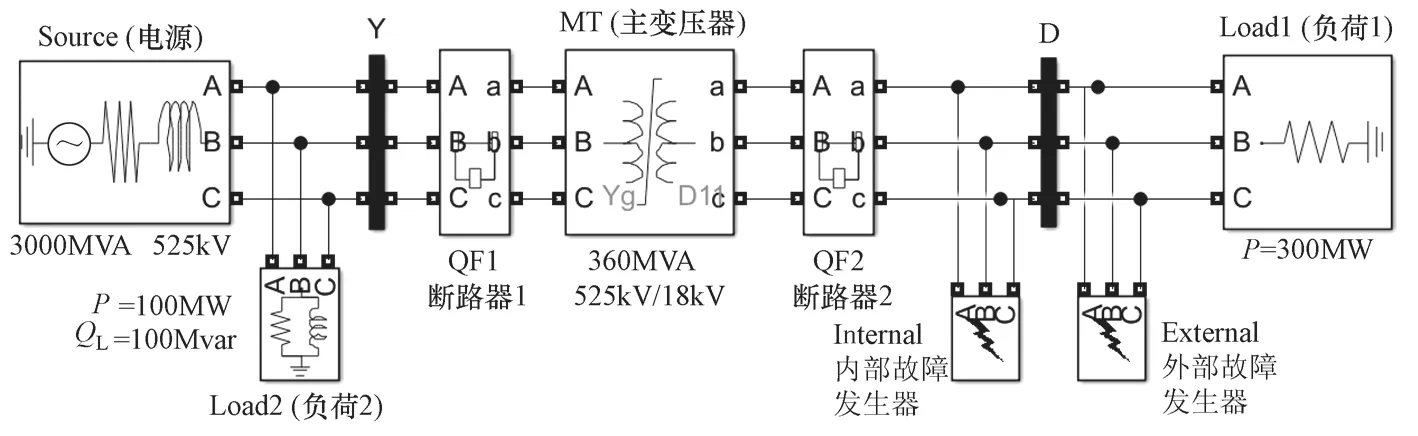
图3 主变压器保护仿真模型Figure 3 Simulink model for transformer relay protection

根据该主变压器出厂试验报告的空载试验结果和短路试验结果，计算并设置主变压器仿真模块的漏抗参数和励磁支路参数。

2.2 变压器差动保护仿真分析

以主变压器保护区内低压侧发生BC两相接地为例进行分析。设置断路器QF1和QF2闭合，故障发生器Internal在0.04s时产生BC两相接地，启动仿真，通过三相电流电压测量模块Y和D将主变压器两侧电流波形数据保存到Matlab工作空间。同步示波器程序读取数据，显示结果如图4所示。

任意指定一个时刻，都可以从界面最右边观察到主变压器两侧线电流的各种信息，包括采样值、各序分量的相量、谐波的相量，还可以在界面左边观察到同步显示的基波序分量相量的矢量图，可以利用这些信息快速判断主变压器当前状态，并进行简单的分析和计算。

当t=30ms时，系统正常运行，电流二次值的有效值如表1所示。

从表1数据可见，低压侧线电流超前于高压侧对应相别线电流约30°，这正是YNd11接线变压器的特点。将电流二次值转换为一次值，高低压侧电流分别为312.5A/9150A，电流比约为0.0342，而两侧额定电流比约为0.0343。因此，同步示波器对稳态时的波形分析正确。

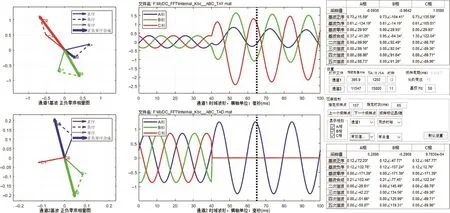
图4 主变压器低压侧保护区内BC两相接地短路故障波形Figure 4 Waveforms for phase B and phase C earthing fault in the protected domain

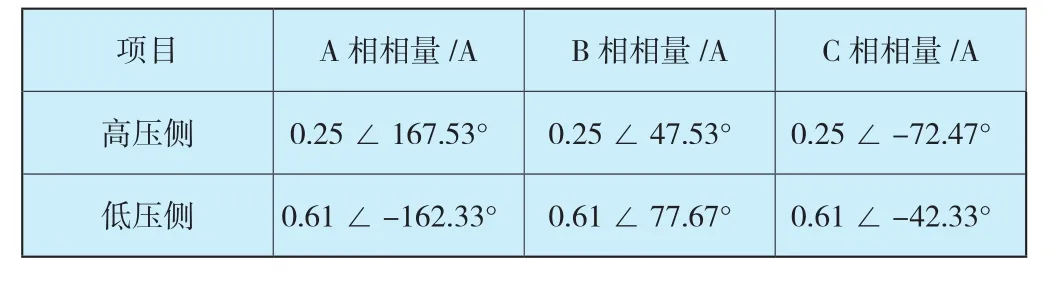
表1 正常运行时主变压器高低压侧三相的线电流二次值（有效值）Table 1 Secondary current（RMS） on both sides of normal transformer

在故障发生后某一时刻，比如t=65ms，主变压器两侧电流数据如表2所示。为了便于观察，将低压侧电流向高压侧进行相位和幅值调整。

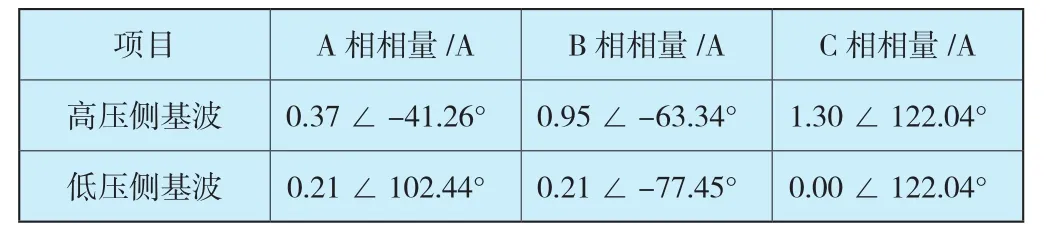
表2 故障时主变压器高低压侧三相线电流数据分析（有效值）Table 2 Analysis for secondary current（RMS）on both sides of fault transformer

该抽水蓄能电站的主变压器保护装置为PCS-985TW，根据该保护装置的说明书，差动电流和制动电流的计算公式为：

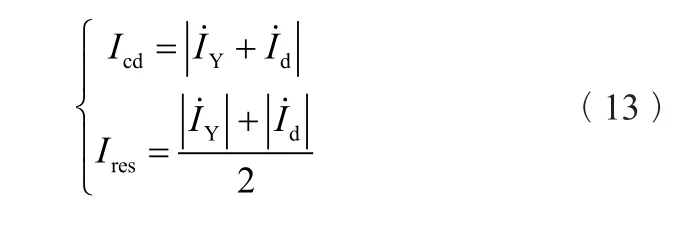
式中Icd、Ires——差动电流和制动电流，A；

、——Y侧和d侧线电流相量，A。

按式（13）计算各相差动电流分别为0.2361A、1.1548A、1.3A，各相制动电流分别为0.29A、0.58A、0.65A，B相和C相差动电流远大于制动电流，且此时二次谐波几乎为零，没有闭锁差动，则主变差动保护将会动作。

2.3 变压器空载合闸涌流分析

主变压器空载合闸时，主变压器铁芯磁通剧增，导致铁芯励磁电流剧增且畸变，此即为空投变压器的励磁涌流。2019年6月，该抽水蓄能电站实施电力系统倒送电，1号主变压器进行了5次冲击合闸。该操作的原理接线仍可引用图3的仿真模型，但是要清除故障发生器Internal和External的设置，断开断路器QF2，即主变压器低压侧空载，然后设置断路器QF1在某时刻合闸。

用本文开发的同步显示示波器对涌流波形进行分析，让软件读取该主变压器冲击操作时产生的故障录波器数据文件，在本示波器上显示如图5所示。为了清晰地观察涌流细节，本次分析只截取了前5个涌流波幅，而且因为主变压器低压侧空载，可以认为其电流为零，因此无需显示和分析低压侧电流。

从同步示波器可见，由于磁通剧增，导致励磁电流畸变为尖顶波，且有间断角出现，这是励磁涌流的典型特征。任取一个时刻，比如第85ms时，示波器显示此时相关分析结果如表3所示。

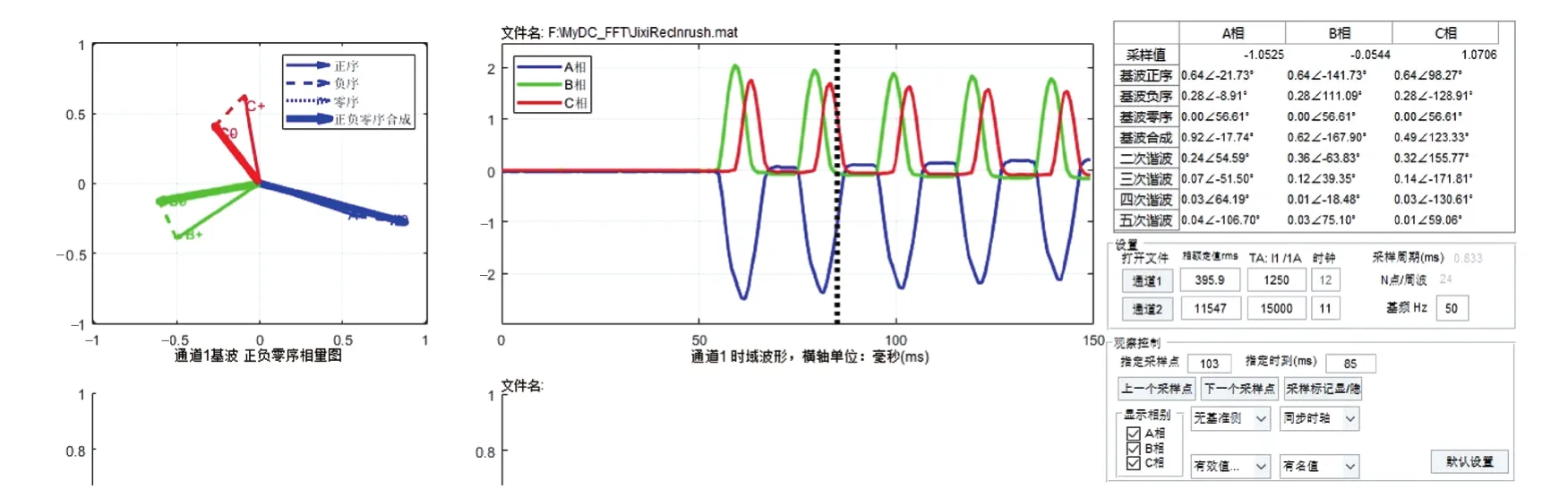
图5 变压器空载合闸时的涌流波形Figure 5 Inrush current of no-load transformer switched to grid

因主变压器低压侧无电流，而且高压侧电流值足够大，差动保护将会动作，但三相的二次谐波电流比达分别达到了26.09%、58.06%、65.3%，远超保护装置二次谐波制动系数整定值15%，因此，二次谐波将会可靠地闭锁差动保护。

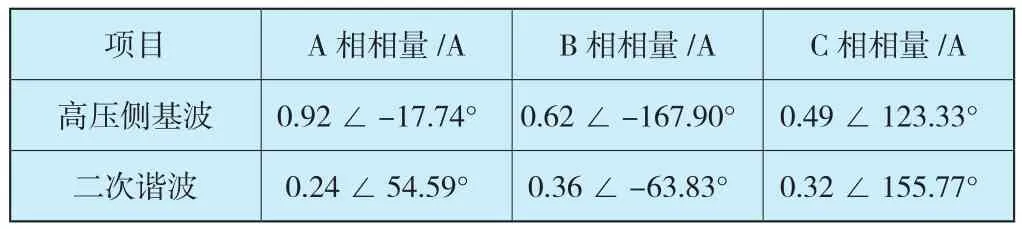
表3 空投主变压器时的励磁涌流（有效值）Table 3 Inrush current（RMS） of noload transformer switched to grid

3 结束语

在应用Matlab/Simulink开展研究时，无法同步观察时域波形和相量图，也不能分析任意时刻的电流电压波形的序分量和谐波分量。针对这两个问题，本文综合运用相关信号处理技术，自主开发了同步显示示波器，彻底解决以上问题，为开展研究工作提供了分析和观察手段。本文研究成果可应用于继电保护仿真研究，也可应用于生产运行中的故障录波数据分析，具有一定的实际意义。