薄壁锐孔孔板流量计算方法比较分析
夏 智,陈平平
(1.中国五环工程有限公司,湖北 武汉 430223;2.福建联合石油化工有限公司,福建 泉州 362800)
作为节流元件的一种,孔板广泛应用于工业实践中。在化工系统设计过程中,孔板应用主要有以下几类:①作为管道元件限制流体的流量或降低流体的压力;②作为孔板流量计的一次元件。而针对不同的用途,不同的研究者所采用的计算方法也不尽相同,因而不同的行业标准规范、书籍、专业软件中孔板的计算公式各不相同,这也导致在实际工程计算过程中对不同的公式难以选择,也难以判断其准确性。
因此,笔者基于Bendict[1]的工作,从一般的单相流薄壁孔板流通方程出发,对常用的孔板流量计算公式进行比较分析,可以发现不同计算方法所采用的简化假设的适用范围,从而判断其准确性,用于指导工程实践。
1 单相流孔板的一般流通方程
单相流孔板的流动见图1,在a截面前流体未受孔板节流的影响,b截面为孔板处截面,c截面处流束收缩最小,平均流速最大。由于篇幅所限,这里不给出计算单相流孔板流量具体的推导过程,仅给出一般公式,其本质上是基于动量守恒方程和绝热方程推导得到的[1]。
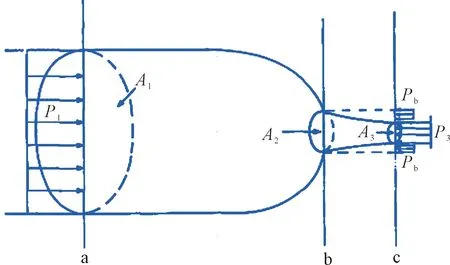
图1 孔板流形示意
1.1 不可压缩流体
(1)
1.2 可压缩流体
(2)
其中,qm为孔板流通的质量流量;p为压力;ρ为密度;A为截面积;Cc为收缩系数,即Cc=A3/A2,一般Cc=0.5-1;Cv为速度系数,即在c截面处实际流速与理想流体流速的比值,用于表征实际能量损失;β为b截面直径与a截面直径比,即β=d/D;k为等熵指数指数,一般情况可以取理想气体绝热指数。
通过上述公式,Benedict[1]将实际流体与理想流体的偏离主要用Cc和Cv进行表征,而这两个参数可以通过关联不可压缩流体下的Cc,i和Cv,i来计算得到,而不可压缩流体经过孔板的流量公式,不论在实验还是理论上都得到了广泛的研究和验证,较为可靠。
2 常用孔板计算公式的比较分析
2.1 化工工艺系统工程设计规定
作为化工行业应用较为广泛的规范,HG/T 20570—95[2]中的孔板流量计算公式见(3) (4)。
2.1.1 可压缩流体
w=43.78·C·d2
(3)
其主要的使用限制是:限流孔板后压力不能小于板前压力的55%。
2.1.2 不可压缩流体
(4)
对比式(4)和(1),可以发现
(5)
通过比对文献值[1]和HG/T 20570附图中的数据,发现二者大体一致,但是由于HG/T 20570取的压差是孔板前和后系统的背压,而流体在最小流束截面(c截面)处的压力小于背压,因此计算出来的流通量会偏低,孔径比越大,偏差越大。此外,由于在HG/T 20570中,可压缩流体和不可压缩流体采用的流量系数C是相同的,但是对比(3)和(2)不难发现。
(6)
而且根据文献数据[1]会发现,Cc与Cc,i的比值随孔板前后压差变大而变大,最大可能偏差150%。因此,HG/T 20570可压缩流体的流量系数C偏小,相同孔径下计算孔板流通量偏小。
由此,初步可以得出这样的结论:在精度不高的情况下,HG/T 20570孔板流量计算公式可用于不可压缩流体,但在计算可压缩流体时孔径偏大。
2.2 孔板流量计算公式
孔板的另一个主要应用就是作为流量测量的一次元件,因此,流量计量相关领域对孔板的计算也有相当广泛的研究,其中,GB 2624-2006[3]给出了标准孔板下的流量计算公式。
(7)
(8)
其中,ε是气体膨胀系数,表征可压缩流体和不可压缩流体的偏离,仅用于前后压差小于0.75的情况中。
对比式(7)、(8)和(1),可以发现:
(9)
二者从形式上是比较贴近的,通过比对文献值[1]和GB 2624的计算值,二者也大体一致。同时,对比(9)和(2),可以发现:
(10)
当Cc=Cc,i=1和Cv=Cv,i时,式(10)和GB 2624中给出的文丘里或喷嘴的可压缩系数是一致的,这也是合理的,因为在文丘里或喷嘴结构下,可以认为流体的最小流通面积即为喉径的面积,即Cc≈1。对孔板而言,Cc与Cc,i的比值随孔板前后压差变大而变大,因此孔板的可压缩系数大于文丘里或喷嘴的可压缩系数,这和式(8)的计算结果是一致的。
在适用范围内,GB 2624所给出的计算方法无疑是相当准确的。但是,对于可压缩流体前后压差大于0.75的情况下,GB 2624并没有给出可选择的计算方法。
2.3 炼油装置工艺管道安装设计手册
《炼油装置工艺管道安装设计手册》下册[4]中的孔板流量计算公式见式(11)。
(11)
对比式(11)、(7)和(1)发现,该方法和GB 2624的公式形式基本是一致的,主要的区别在于流量系数和膨胀系数的关联公式的选取。但是由于流量系数和膨胀系数需要查图表得到,因此计算较为繁琐,不利用工程应用,本文不对该方法进行进一步讨论。
此外,式(11)对前后压差不做限制,可用于临界流情况,但实际上这和理论是违背的,只是一种工程上的简化处理办法。
2.4 Idelchik公式
Idelchik[5]针对不可压缩流体给出了锐孔薄壁孔板的流量经验关联公式(12),与其他公式的区别主要在于流量系数的关联式不一样,对于可压缩流体,该关联式不适用。
(12)
2.5 计算结果比较分析
由于方法2.2和方法2.3在本质上是一样的,而且GB 2624推荐的方法显然是更为可靠的,因此主要对比方法2.1、方法2.2和方法2.4。
2.5.1 不可压缩流体
对于不可压缩流体,选取30℃水为研究对象,板前压力为6.0MPa(a),板后压力为4.8MPa(a),管道直径为50mm,针对不同孔径比,计算结果见表1。
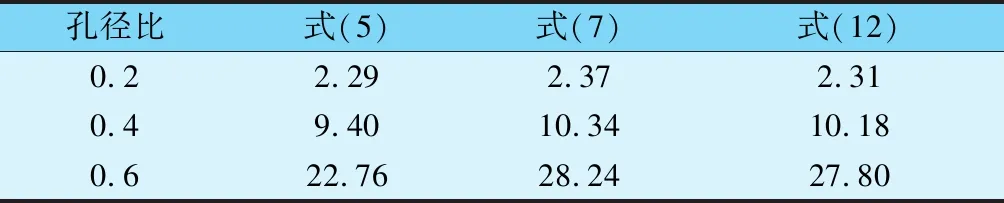
表1 不可压缩流体不同孔径比下的流量/(kg·s-1)
通过分析上述数据不难发现,在低孔径比的情况下,3个公式计算结果相差不大,但是当孔径比增大时,式(5)计算结果有较大偏差,这与之前理论分析的结果一致。此外,式(11)的形式最为简单,工程应用最为方便。
2.5.2 可压缩流体
对于可压缩流体,选取30℃氮气为研究对象,板前压力为6.6MPa(a),管道直径为100mm,孔直径为20mm,针对不同压比,计算结果见表2。
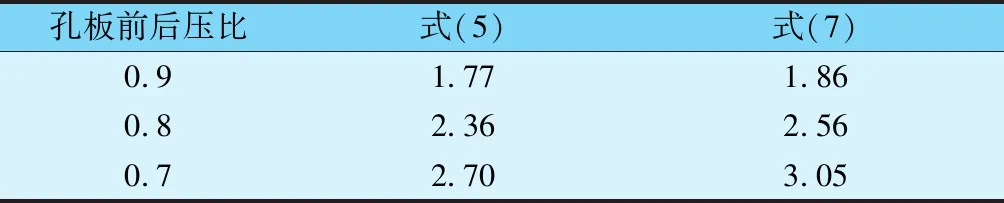
表2 可压缩流体不同孔径比下的流量/(kg·s-1)
通过分析上述数据不难发现,在低压比的情况下,二者计算结果相差不大,但是当压比减小时,式(5)计算结果有较大偏差,这个与之前理论分析的结果一致。此外,虽然式(7)在压比小于0.75的情况下不适用,但是在精度要求不高的情况下可以做小范围的外推。
3 临界压比下孔板的流通系数
在工程应用过程中,经常会遇到可压缩流体孔板前后压比小于或等于临界压比的情况,而且在对精度要求不高的情况下,通常考虑采用单孔板来实现。只有式(5)和(11)对这类情况给出了计算方法。但是通过第2节的讨论不难发现,(5)的计算结果存在较大偏差,因此并不适用。而仔细分析式(11)后发现,其形式本身是不能用于临界流情况的。因为,当孔板前后压比小于临界压比时,流体在最小流束截面处的压力始终为临界压力,并不会随着孔板前后压差变大而降低,所以,虽然式(11)可以在一定程度上计算临界流的情况,但实际上只是一种工程化的近似,其准确性难以确定。
对于临界流,可以用一般的流通方程(2)来进行描述。当发生临界流时,孔板最小流束截面处的压力恒定为临界压力,即:
(13)
结合式(2)则有:
(14)
当发生临界流时,由于流体的最小流束截面积会随着前后压差变大而变大,因此,通过孔板的流量会随着孔板前后压差变大而变大,但是,由于孔板结构的原因,其最小流动面积总会比孔板小孔面积小,因此Cc<1。再结合Bendict[1]的工作,可以初步给出如下结论:①对于可压缩流体在锐孔薄壁孔板下,当孔板后压力接近大气压,且对计算准确性要求不高时,可以选取Cc=0.86,Cv=0.97;②对于可压缩流体在锐孔薄壁孔板下,当孔板后压力接近大气压时,在需要尽可能限制流体流速、保守处理的情况下,可以选取Cc=1,Cv=0.97。
4 结语
本文从一般的单相流孔板流通方程出发,通过
对上述常用的孔板计算公式进行比较分析,并讨论了各种常用计算方法的适用范围和局限性,可以指导在实际工程应用过程中选取合适的计算方法。具体分析结果如下:①在对工程计算有较高准确性要求时,在GB 2624适用范围内,优先使用GB 2624对孔板进行计算;②在对工程计算有一定准确性要求时,对于不可压缩流体,可以用Idelchik公式对孔板进行简化计算;③对于前后压差较大,或孔径比较大时,不建议采用HG/T 20570进行计算;④对于可压缩流体的临界流情况,可以根据炼油装置工艺管道安装设计手册公式进行试算,也可以根据本文建议的方法进行保守性估计。如果对孔板流量的计算精度有较高要求时,建议采用多板来逐级减压。

