一种用表达式描述TRIZ理论的方法

黄振永 薛竣文

摘 要：TRIZ理论常直译为“发明问题的解决理论”，曾是前苏联的国家机密，现在广泛应用于各行各业，被誉为创新的“点金术”。现有的TRIZ理论中的九屏幕法、STC算子法、物场分析模型采用的是图示法，而图示法具有显著的缺点：绘图复杂、占用面积大。该文提出了一种用表达式描述TRIZ理论的方法，消除了图示法的缺点。该文把这种新方法应用于九屏幕法、STC算子法、物场分析模型，并通过案例诠释了其使用方法，有创新性和应用价值。

关键词：TRIZ理论  表达式描述法  九屏幕法  STC算子  物场分析模型

中图分类号：TS43           文献标识码：A        文章编号：1672-3791（2021）11（a）-0000-00

The Method of Describing Triz Theory by Expression

HUANG Zhenyong  XUE Junwen

（School of Information Technology， Beijing Institute of Technology， Zhuhai，Zhuhai， Guangdong Province， 519088 China）

Abstract： TRIZ theory is often translated as "The Solution Theory Of Invention Problems". It was once a state-level secret of the former Soviet Union. Now it is widely used in all walks of life. It is known as the "Golden Touch" of innovation.The nine screens method， STC operator method and material-field analysis model in the existing TRIZ theory adopt the graphical method， which has significant disadvantages： complex drawing and large occupied area.This paper presents a method to describe TRIZ theory by expression， which eliminates the shortcomings of graphical method. This paper applies this new method to nine screens method， STC operator method and material field analysis model， and their use methods are explained through cases.This expression description method has innovation and application value.

Key Words： TRIZ theory; Expression description method; Nine screens method; STC operator; Material field analysis model

TRIZ是拉丁文“Teoriya Resheniya Izobreatatelskikh Zadatch”的詞头缩写，其英文全称是“Theory of the Solution of Inventive Sroblems”，常直译是“发明问题的解决理论”，也常意译为“萃智”或者“萃思”，取其“萃取智慧”或“萃取思考”之义[1-2]。它是由前苏联发明家、教育家G.S.Altshuller（根里奇·阿奇舒勒）在1946年创立的理论[3]。它曾是前苏联的国家机密，在军事、工业、航空航天、管理等领域均发挥了巨大作用，被誉为创新的“点金术”[4-5]。经过70多年发展，TRIZ理论已经发展成为一套解决新产品开发实际问题的成熟的理论和方法体系[6-7]。因为TRIZ理论具有好系统性、操作性和实用性，所以它在全球的创新和创造学研究领域占据着独特的地位。实践证明，TRIZ理论可以帮助人们突破思维障碍，打破思维定势，加快人们创造发明的进程，并能得到高质量的、有竞争优势的创新产品[3-4，6]。由于目前TRIZ理论中的九屏幕法、STC算子法、物场分析模型采用的是图示描述法，具有显著的缺点：绘图复杂、占用面积大。该文提出了一种用表达式描述TRIZ理论的方法，消除了图示法的缺点，具有结构紧凑的优点和较高的推广价值。

1 九屏幕法

现有的九屏幕法是一个“框+箭头”的图示法结构[7]，缺点是：绘图时操作复杂且占用面积大。革新后的九屏幕法是二维表格（3行×3列）。借鉴解析几何学的数对知识，交叉单元格的表示方法：S（x，y），其中S是“Scree”的首字母，x表示时间维，x=-1表示过去，x=0表示现在，x=1表示未来;y表示层级维，y=-1表示子系统，y=0表示当前系统，y=1表示超系统。

如果令S（0，0）={当前系统}，S（-1，0）={当前系统的过去}，S（1，0）={当前系统的未来}，S（0，1）={当前超系统}，S（0，-1）={当前子系统}，S（-1，1）={超系统的过去}，S（1，1）={超系统的未来}，S（-1，-1）={子系统的过去}，S（1，-1）={子系统的未来}，则革新后的（省略箭头并合并框为表格的形式）九屏幕法的表达方式如表1所示。如果进一步地令S0=S（0，0）、S1=S（-1，0）、S2=S（1，0）、S3=S（0，1）、S4=S（0，-1）、S5=S（-1，1）、S6=S（1，1）、S7=S（-1，-1）、S8=S（1，-1），S的右下角数字是按习惯性填表顺序编码的，则简化后的九屏幕法的表达方式如表2所示。

如果遇到的是反系统则在S的右上角加上一撇，记作：S’（x，y），因此如表3所示。反系统的简化表达方式如表4所示。

2  STC算子法

STC算子有3个：S（Size，尺寸）、T（Time，时间）和C（Cost，成本）[3]。STC算子法是将尺寸、时间、成本进行极限化分析的思维方法。现有的表达方式是三维坐标法，缺点是：作图时占用面积大。

革新后的表達方案如下：

算法1：P_1=lim┬（S→∞）⁡{方案}，表示：当尺寸趋向无限大时的解决方案。

算法2：〖P_2=lim┬（S→0）〗⁡{方案}，表示：当尺寸趋向零时的解决方案。

算法3：〖P_3=lim┬（T→∞）〗⁡{方案}，表示：当时间趋向无限大时的解决方案。

算法4：〖P_4=lim┬（T→0）〗⁡{方案}，表示：当时间趋向零时的解决方案。

算法5：〖P_5=lim┬（C→∞）〗⁡{方案}，表示：当成本趋向无限大时的解决方案。

案例：以上课考勤为研究对象。

算法1：P_1=lim┬（S→∞）⁡{当学生人数趋向于无限大的解决方案}。

算法2：〖P_2=lim┬（S→0）〗⁡{当学生人数趋向于零的解决方案}。

算法3：〖P_3=lim┬（T→∞）〗⁡{当考勤时间趋向于无限大的解决方案}。

算法4：〖P_4=lim┬（T→0）〗⁡{当考勤时间趋向于零的解决方案}。

算法5：〖P_5=lim┬（C→∞）〗⁡{当考勤成本趋向无限大的解决方案}。

算法6：〖P_6=lim┬（C→0）〗⁡{当考勤成本趋向于零的解决方案}。

3 物场分析模型

3.1 五种物场分析模型的表达方法

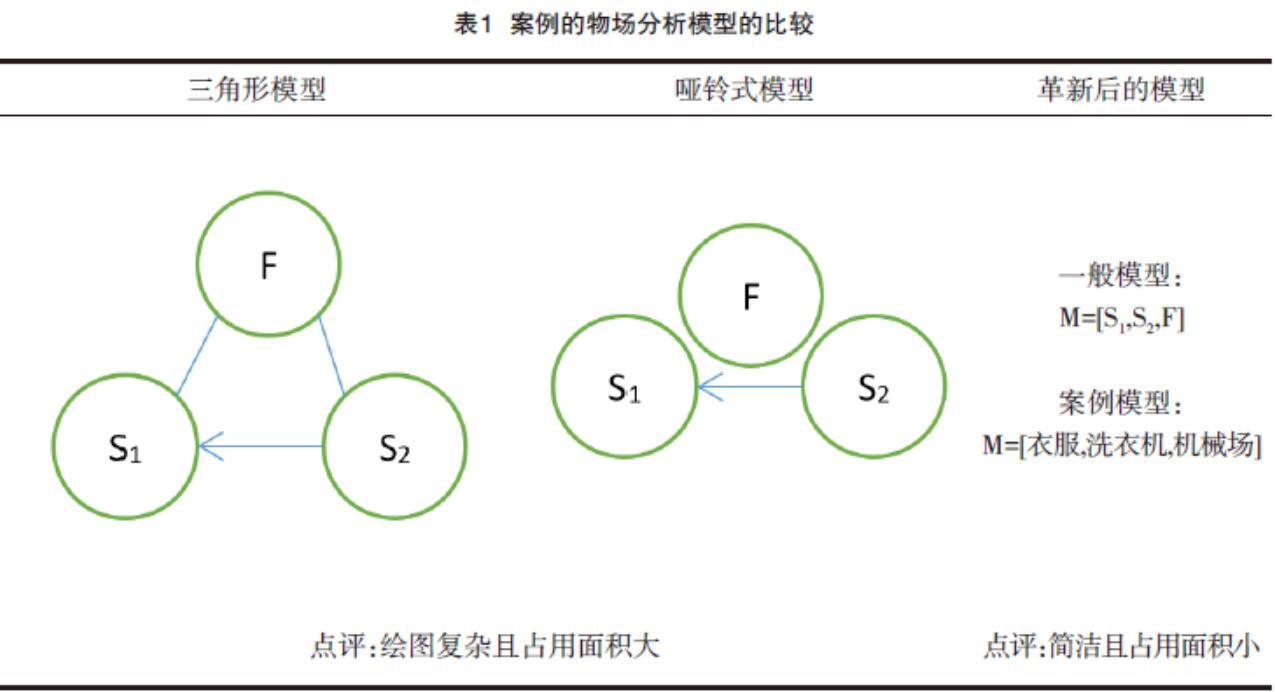
现有的物场分析模型的表达方式是：三角形图示法、哑铃式图示法，缺点是：作图时复杂占用面积大。物场分析模型的三要素：S1：作用对象（也称工件，受作用体，下文简称：受体），S2：作用工具（也称施作用体，下文简称：施体），F：场。此外，S3：第三种物质，F2：新场[1-2]。

革新后的方案如下：

用表达式法表达物场分析模型的一般模型：M=[S1，S2，F]，释义：模型=[受体，施体，场]。

用洗衣机洗衣服的案例模型比较如表5所示。

一般模型：

M=[S1，S2，F]

案例模型：

M=[衣服，洗衣机，机械场]

点评：绘图复杂且占用面积大 点评：简洁且占用面积小

3.1.1 模型1：完整且作用充足模型

顾名思义，它是指3个元素齐备且作用充足的模型。该模型的一般形式：M=[S1，S2，F]，用“[ ]”表示在F的作用下，S2对S1提供有效且充足的作用，比如：洗衣机把衣服洗干净了，模型为：M=[衣服，洗衣机，机械场]，又如：用水取出掉入树洞的球，模型为：M=[球，水，浮力场]。

3.1.2 模型2：不完整模型

当缺少3个元素的1或2个元素时，它就是不完整模型。该模型的一般形式：

缺一个元素时：M=[S1， ， ]、M=[ ， S2， ]、M=[ ， ， F];

缺两个元素时：M=[S1， S2， ]、M=[S1， ，F ]、M=[ ， S2， F]。

比如：只有洗衣机的模型：M=[ ，洗衣机， ]，注意：元素分隔符号（，）不能因为元素的缺失而省略。同理，只有衣服的模型：M=[衣服， ， ];只有场的模型：M=[ ， ，机械场];如果有衣服和洗衣机但停电了（没有机械场），则模型：M=[衣服，洗衣机， ]。

3.1.3 模型3：完整但作用不充足模型

它是指3个元素齐备但作用不充足的模型，用“（ ）”表示在F的作用下，S2对S1提供有效但不足的作用。该模型的一般形式：M=（S1，S2，F）。比如：洗衣机没有把衣服洗干净，模型为：M=（衣服，洗衣机，机械场）;又如：人在冰面上行走因摩擦力小会摔倒，模型为：M=（鞋，冰，摩擦力）。

3.1.4 模型4：完整但作用过度模型

它是指3个元素齐备但作用过度的模型，用“{ }”表示在F的作用下，S2对S1提供有效但过度的作用。该模型的一般形式：M={S1，S2，F}。比如：手拿纸杯，因用力过度把被子捏变形了，模型为：M={纸杯，手，机械场};煎鱼时因开大火温度过高鱼被煎糊了，模型为：M={鱼，锅，热场}。

3.1.5 模型5：完整但作用有害模型

它是指3个元素齐备但作用有害的模型，用“< >”表示F的作用下，S2对S1提供有害的作用。该模型的一般形式：M=<S1，S2，F>。比如：手拿玻璃杯子，杯子上的裂纹把手划伤了，模型为：M=<手，玻璃杯，机械场>，注意：因为是杯子把手划伤了，所以此时的S1是手，S2是玻璃杯;在木板上钉钉子，取出钉子后，木板上留下一个钉洞，模型：M=<木板，钉子，机械场>。

3.2 物场分析模型的6种一般解法的表达方法

3.2.1 一般解法1（针对不完整模型有效）

该解法是指补齐物场模型中所缺失的元素，从而构造完整有效的模型。案例如下：

问题：想把钉子钉入木板，却发现缺少锤子。

解法：寻找锤子或可替代物，补齐缺失的元素。

模型：M=[钉子， ，机械场]=>M=[钉子，锤子，机械场]

释义：把一个不完整模型转变为完整模型，其中“=>”表示模型转变的意思。

归纳一般解法1的一般形式：

缺一个元素时：M=[S1， ， ]=>M=[S1，S2，F];M=[ ， S2， ]=>M=[S1，S2，F];M=[ ， ， F]=>M=[S1，S2，F];

缺两个元素时：M=[S1， S2， ]=>M=[S1，S2，F];M=[S1， ，F ]=>M=[S1，S2，F];M=[ ， S2， F]=>M=[S1，S2，F];

注意：缺零个元素等价于完整模型，缺3个元素是无意义的，因此主要关注以上两种情况。

3.2.2 一般解法2（针对完整但作用有害模型有效）

该解法是增加第三种物质S3（也可能是由S1、S2演变而来的）来阻止或降低有害作用。案例如下：

问题：普通透明玻璃无法保护房间内的隐私。

解法：可以在玻璃上贴一张纸使视觉模糊，或者表普通玻璃替换成磨砂玻璃。

模型：M=<隐私，普通玻璃，光场>=>M=[隐私，磨砂玻璃，光场]+[贴纸]

M=<隐私，普通玻璃，光场>=>M=[隐私，磨砂玻璃，光场]

释义：如果是需要添加的元素，则写在后面，如果是替换元素，则直接在原位置替换。

归纳一般解法2的一般形式：

M=<S1，S2，F>=>M=[S1，S2，F]+[S3]

释义：引入第三种物质S3（如引入催化剂可以加速化学反应进程）。

M=<S1，S2，F>=>M=[S1，S2，F]+[S’1]

释义：引入由S1演变的第三种物质S’1（如把常温焦炭铺在传送带上，以防止热焦炭损伤传送带，这里的S1是热焦炭，S’1是降温到常温的焦炭）。

M=<S1，S2，F>=>M=[S1，S2，F]+[S’2]

释义：引入由S2演变的第三种物质S’2（如用糯米纸包裹糖块，再用塑料纸包装，这里的S2是塑料纸，S’2是糯米纸）。

3.2.3 一般解法3（针对完整但作用过度模型有效）

该解法是引入另外一个场F2来阻止或降低过度作用，必要时添加第三种物质S3。案例如下：

问题：用手拿塑胶杯喝水时，常常因用力过大导致杯子变形。

解法：使用杯托。

模型：M={塑胶杯，手，机械场}=>M=[塑胶杯，手，机械场]+[杯托，机械场]

归纳一般解法3的一般形式：

M={S1，S2，F}=>M=[S1，S2，F]+[F2]

3.2.4 一般解法4（针对完整但作用不充足模型有效）

该解法是用另外一个场F2来替代原有的场F。案例如下：

问题：在导体两端加一个热场，因为自由电子做无规则热运动，不能形成电流。

解法：把热场替代为电场，使电子在电场作用下做定向运动，从而形成电流。

模型：M=（电子，导体，热场）=>M=[电子，导体，电场]

归纳一般解法4的一般形式：

M=（S1，S2，F）=>M=[S1，S2，F2]

3.2.5 一般解法5（针对完整但作用不充足模型有效）

该解法是增加另外一个场F2来强化有用作用。案例如下：

问题：用洗衣机和室温水洗衣服时，顽固污渍洗不干净。

解法：将洗衣机的水加热，引入高温热场。

模型：M=（衣服，洗衣机，机械场）=>M=[衣服，洗衣机，机械场]+[热场]

归纳一般解法5的一般形式：

M=（S1，S2，F）=>M=[S1，S2，F]+[F2]

3.2.6 一般解法6（针对完整但作用不充足模型有效）

该解法是引入第三种物质S3（也可以由S1或S2演变而来）并增加一个场F2来强化有用作用。案例如下：

问题：火柴杆在装入盒子里时，头尾摆放顺序常常不一致。

解法：在火柴头里加入少量的磁粉，并借助磁场使头尾摆放顺序一致化。

模型：M=（火柴，装盒设备，机械场）=>M=[火柴，装盒设备，机械场]+[磁粉，磁场]

归纳一般解法6的一般形式：

M=（S1，S2，F）=>M=[S1，S2，F]+[S3，F2]

4 结语

经过70多年的发展，TRIZ理论在各行各业取得了广泛应用，是科技创新的利器，其理论体系日益完善。美中不足的是几乎所有现有的文献中的九屏幕法、STC算子法、物场分析模型采用的是图示法，在制作教学课件时发现其存在显著的缺点：绘图复杂、占用面积大，给备课带来了不便。该文提出了一种用表达式描述TRIZ理论的方法，并結合案例进行了解释与应用，该方法消除了图示法的缺点，具有较高的推广价值。

参考文献

[1] 黄振永，裴雪丹，王利利，等.LED灯具的TRIZ物-场分析模型及其简化表达法[J].科技资讯，2019，17（9）：1-4.

[2] 黄振永.一种TRIZ理论中物-场分析模型的简化表达方法[J].今日财富，2019（2）：55-56.

[3] 王春阳.基于TRIZ改善红外连续变焦镜头光轴一致性研究[D].昆明：昆明理工大学，2021.

[4] 孙瑶，姚智泉，姚囧明.基于Triz理论下的大型古壁画摹制法的创新设计[J].科技创新导报，2020，17（18）：254-256.

[5] 张瑜，杨嘉悦，易湘斌，等.TRIZ创新方法融入应用型大学创新创业教育的研究与实践[J].文化创新比较研究，2020，4（10）：135-136.

[6] 李金凤，赵继云，侯秀宁，等.采用TRIZ理论的豌豆割晒机械装备设计与试验[J].农业工程学报，2020，36（8）：11-20.

[7] 苏珂，崔元.面向相似认知用户集群的TRIZ超系统资源需求获取模型[J].计算机集成制造系统，2021，27（7）：2065-2077.

基金项目：2021年国内访问学者项目（项目编号：FX20212052）;2021年珠海市哲学社会科学规划课题（项目编号：2021GJ189），2019年度广东省高等教育教学改革项目（项目编号：697）;2019年度校级质量工程及教改项目（项目编号：2019004JXGG和2019003JXTD）。

作者简介：黄振永（1979—），男，硕士，讲师，研究方向为光电技术和TRIZ理论。

DOI：10.16661/j.cnki.1672-3791.2110-5042-8847