面向异构超算的结构分析高效并行计算方法*

丁峻宏,苗新强,李根国

(1.上海超算科技有限公司，上海 201203;2.中国电子科技集团公司第五十一研究所，上海 201802;3.上海超级计算中心，上海 201203)

1 引言

当前，在很多科学和工程研究领域为了提高计算分析的规模和效率，通常采用超级计算机进行并行计算[1 - 3]。其中，有限元和计算机技术的融合和快速发展使其被广泛应用于航空、汽车、土木和建筑等许多工程领域。在进行大规模并行计算时，往往需要根据超级计算机的硬件体系结构特点设计出合适的并行算法，以充分发挥其高效的计算性能。

传统的超级计算机在每个结点内配置的计算设备比较单一，一般只配置CPU，被称为同构型超级计算机[4]。近年来硬件加速技术的飞速发展使得新型研制的超级计算机倾向于在每个结点内部配置不同性能的计算设备，除了配置CPU外，还配置有协处理器，如图形处理器GPU(Graphic Processing Unit)[5]和众核处理器MIC(Many Integrated Core)[6]，这也就催生了异构型超级计算机。对于传统的同构型超级计算机，国内外一些学者提出了不少好的方法。例如，针对共享存储的同构型超级计算机提出了循环级的细粒度并行计算方法[7]，而针对分布式存储的同构型超级计算机提出了任务级的粗粒度并行计算方法[8]。在异构超级计算机中最早是采用GPU作为协处理器，很多学者也对其有一定的研究[9 - 11]。异构型超级计算机从采用Intel公司推出的MIC作为协处理器开始，将并行计算从多核时代带入了众核时代[12]。对适合异构众核超算的并行计算方法的研究目前处于不断探索阶段[13 - 15]，相关的研究还不是太多。

本文尝试探索异构众核架构下有限元结构分析的并行优化方法，研究有限元结构分析与高性能计算平台的最优适配方法，为同类应用问题的并行移植和性能优化提供借鉴与参考。

2 结构分析并行计算与异构众核计算平台

2.1 结构分析并行计算

结构分析平衡方程可以表达为：

Kx=P

(1)

其中，K为总体刚度矩阵，P为总体外部载荷向量，x为位移向量。

利用区域分解法进行有限元结构分析并行计算的基本原理[16]如下所示：

首先将总体网格模型分为数个子区域；然后按照先内部自由度后边界自由度的编号原则同时独立形成每个子区域的系统方程：

(2)

其中，xI,xB,PI,PB分别为内部节点和边界节点对应的位移和外部载荷向量;K**为刚度矩阵中的分块矩阵，其中下标I和B分别表示内部自由度和边界自由度。

通过缩聚同时独立消去各子区域内部节点自由度后，得到只含边界节点自由度未知量的界面方程:

(3)

其中有效刚度矩阵:

(4)

有效载荷向量:

(5)

接着将所有子区域的界面方程联立求解，得到各子区域边界节点位移。根据求得的边界节点位移xB，各子区域内部节点位移xI由式(6)回代求解:

xI=(KII)-1(PI-KIBxB)

(6)

计算各子区域的应变值和应力值，并分别输出结果。

2.2 异构众核计算平台

“天河二号”异构众核超算包含1.6万计算结点(单结点配置2颗Intel Xeon E5 多核处理器和3块Intel Xeon Phi众核处理器)。结点间互连采用自制主干拓扑结构网络，网络接口使用NIC控制器。

传统区域分解法应用在同构型超级计算机上效果很好，但应用在异构众核超级计算机上时却会面临一些问题。这是由于异构众核超级计算机在大幅度提升系统计算性能的同时也为高效并行计算方法的设计带来了一定的挑战：首先MIC的计算性能与CPU相比迥异，因此如何实现CPU与MIC设备之间以及不同结点之间的负载均衡成为迫切需要解决的问题。其次，在异构众核超级计算机中不同结点、设备以及计算核心间的通信延迟差异显得更加突出，而通信延迟是制约大规模并行计算效率的主要因素之一，故如何提高系统的通信效率成为并行计算方法设计的一个关键问题。最后，每个MIC卡内存空间不大，如何利用有限的内存空间实现大规模并发性计算任务也是需要重点考虑的问题。

3 多层次多粒度协同并行计算方法

从硬件体系结构看，众核架构下异构超算由多计算单元(多核或众核)、多设备(CPU或MIC卡)和多结点的层次性元素构成。在结点之间和设备之间可以考虑使用任务级的粗粒度并行计算方法，而多核或众核的不同计算核心间适合采用循环级的细粒度并行计算方法。为了实现并行计算方法与异构超算平台的最优适配，本文提出了一种针对结构有限元分析的多层次多粒度协同并行计算方法。

3.1 总体方法

多层次多粒度协同并行计算方法基于对计算任务的层次性和粒度性剖析。如图1所示，本文将有限元结构分析的计算作业的并行处理划分为3个不同层面，以与异构众核超算硬件结构相匹配：结点间、设备间和核间。其中前两者使用粗粒度并行方法，而后者使用细粒度并行方法。

Figure 1 Task mapping图1 任务映射

(1)结点间并行。

任务级的粗粒度并行计算方法适合结点间并行，这是由于采用分布式存储的异构众核超算的结点之间通信延迟远远高于结点内部，因此任务级的粗粒度并行计算方法适合于结点之间的并行。这样不仅能够实现大规模并行计算数据的分布式存储，而且可以有效降低通信开销。

如图1所示，结点间并行在区域分解法基础上开展：首先结构有限元网格被划分为M个一级子区域，其中M为并行计算所调用的整体结点数量。每个一级子区域被分别分配给一个计算结点，从而实现结点间的并行计算。由于各计算结点的性能都一致，因此为实现结点间的负载均衡，在进行一级剖分时各子区域的规模也应当相同。

(2)设备间并行。

相对于结点间通信来说，同一结点内不同设备间的通信开销要小一些，但比每个设备内部的核间通信开销还大很多，所以基于区域分解的粗粒度并行计算方法多用于不同设备之间。为最大程度限制设备间的通信在同一计算结点内，应将相邻的子区域分配在一起。

如图1所示，设备间的并行立足于(1)中的一级分区结果：每个一级子区域被进一步分解为(Q+R)个二级子区域，其中Q指的是单个结点内部CPU设备的数目，R则定义为单个结点内部MIC卡设备的数目。然后，每一个设备将单独处理一个二级子区域，从而实现设备间的并行计算。由于各二级子区域均由同一个一级子区域派生而来，这就将相邻的子区域分配在了一起，这样就使得设备之间的通信被限制在同一计算结点内。考虑到MIC和CPU计算性能的表现相差明显，因此在二级分区时分配给CPU设备和MIC设备的子区域规模应有所不同。为尽量在不同设备间寻求负载均衡，本文将特定的计算任务分别分配给CPU和MIC单独计算，以确定二者计算性能的比值，然后据此确定分配给CPU设备和MIC设备的子区域规模的大小。

(3)核间并行。

随着硬件技术的快速发展，异构众核超级计算机在每个结点内集成的计算核心数也越来越多。例如，“天河二号”上每颗CPU配置12个多核计算核心，每个MIC卡配置61个众核计算核心(其中57个可供用户使用)。如此众多的计算核心一方面具有较高的硬件并发计算特性，另一方面这些计算核心间通过共享系统二级缓存和内存具有很高的数据通信效率。若采用基于区域分解的粗粒度并行计算方法利用这些多核或众核资源难免会面临因分区过多而导致系统通信开销增加的问题。而细粒度并行计算方法本身就具备高度的并发性，能够有效利用多核或众核资源较高的硬件并发计算特性。此外，它是基于共享存储实现的，能充分利用多核或众核间共享二级缓存和内存的优势提高系统数据访问效率[17]。因此，本文采用循环级的细粒度并行计算方法实现核间的并行计算。

核间并行将基于每一个二级子区域的计算任务继续作分解，这将触及到处于最底层的计算模块。基于区域分解法进行有限元结构分析并行计算的主要步骤包括：组集子区域系统平衡方程、缩聚、求解界面方程、回代内部自由度以及计算子区域应变和应力。如图1所示，核间并行要做的工作就是基于二级子区域的每个计算步骤，搜寻其中的热点计算程序，即大的循环结构，并将其进一步分解为一批彼此独立、各自执行的子任务，其后CPU或MIC的一个计算核心将被调配去执行每一个子任务。

3.2 多层次多粒度协同并行计算方法的实现

本文采用offload模式实现有限元结构分析的多层次多粒度协同并行计算方法，在通信层面使用MPI+OpenMP实现。如图2所示，有限元结构分析的多层次多粒度协同并行计算流程为：

第1步首先实施两级分区方法，以获取用于结构分析并行所需的计算数据文件，包括M个子区域的节点、单元、载荷和边界条件以及相邻分区信息等。

第2步在CPU端启动执行M*(Q+R)个MPI进程，其中每个进程负责读取和处理一个二级子区域数据文件。

第3步在每一个进程的内部再各自进一步派生出K个线程，并加载到CPU端利用多核资源完成相应子区域总体刚度矩阵和外部载荷向量的计算。其中，K等于单个结点内所有CPU设备的总核数除以单个结点内的进程总数并取整。

第4步与MIC设备相关联的进程首先将子区域的总体刚度矩阵和外部载荷向量加载到MIC卡，在MIC端进一步派生出S个线程并进行缩聚计算，计算结果将最终被传回至CPU端；而与CPU设备相关联的进程则直接在CPU端派生T个线程进行缩聚计算。其中，S等于单个MIC卡总核数的4倍；T等于单颗CPU的总核数。

第5步各进程共同利用并行预处理共轭梯度PCG(Preconditioned Conjugate Gradient)算法求解界面方程，得到各子区域边界节点位移后再回代求解内部位移。其中，求解界面方程时每个进程内部派生出K个线程，以有效利用CPU的多核资源缩短计算量较大的任务的处理时间。

第6步与MIC设备相关联的进程首先将子区域节点位移加载到MIC卡，然后在MIC端派生S个线程回代求解子区域应变/应力，计算结果将被传回至CPU端；而与CPU设备相关联的进程则直接在CPU端派生T个线程计算子区域应变/应力。

第7步如果迭代继续，则流程将跳转至第2步再执行一遍;否则该流程结束。

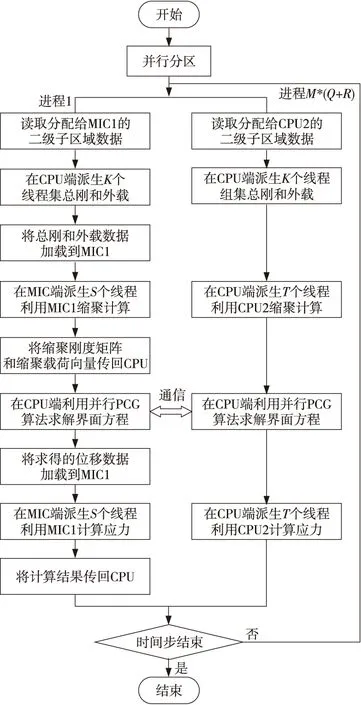
Figure 2 Flowchart of collaborative parallel computing based on multi-layer and multi-grain图2 多层次多粒度协同并行计算流程

3.3 关键技术研究

为保证多层次多粒度并行计算方法的顺利实施，本文主要针对MIC卡的内存瓶颈问题、缩聚算法的高度并发性实现和界面方程的并行求解等核心问题进行研究。

3.3.1 MIC卡的内存瓶颈问题

传统有限元分析程序一般采用变带宽格式存储结构刚度矩阵，由于它不能避免对带宽内大量零元素的存储，因此随着有限元规模的扩大会导致系统内存需求的急剧增加。但是，单个MIC卡配置的内存空间不太大，要利用众核资源进行并行计算首先必须降低系统的内存需求。

近年来，最新发展起来的行压缩存储技术通过仅针对刚度矩阵中的非零元素进行存储，可以大幅度减少系统的内存需求。考虑到CPU设备往往配置有大量的内存空间，并且这些内存空间对同一结点内的所有CPU设备都是共享的，因此本文首先在CPU端采用变带宽格式完成各二级子区域总体刚度矩阵和外部载荷向量的组集，将其转化为占用内存空间较小的行压缩存储格式后再加载到MIC端利用众核资源进行并行计算。

3.3.2 缩聚算法的高度并发性实现

本文通过将缩聚计算转换为一系列相互独立的线性方程组的求解，并利用OpenMP来开展并行化处理，从而实现了整个计算任务的高度并发性执行。本文设计的缩聚算法的伪代码如算法1所示。

算法1缩聚算法

1.//calculate the condensed stiffness matrix

2.!$ompparalleldo

3.doi=1,z

4.b=KIB(:,i)

5. solveKIIt1=bwith a direct sparse solver

6. computet2=KBIt1

8.enddo

9.!$ompendparalleldo

10.//calculate the condensed load vector

11.b=PI

12.solveKIIt1=bwith a direct sparse solver

13.computet2=KBIt1

15.//solve interface equations

17.//calculate internal degrees of freedom

18.b=PI-KIBxB

19.solveKIIxI=bwith a direct sparse solver

3.3.3 界面方程的并行求解

在本文中，并行预条件共轭梯度算法被用于求解界面方程。考虑到求解界面方程的过程中往往需要大量的迭代，将计算数据在CPU和MIC设备间频繁地传输会严重影响系统通信效率，因此本文在求解界面方程时只利用CPU端的多核处理器完成相关的计算工作。对于计算量较小的任务，如向量与向量的和或点积操作，直接交给每个MPI进程完成；而对于计算量较大的任务，如矩阵和向量的乘积，在每个MPI进程内部将进一步派生出许多线程，这样可以有效发挥CPU端的多核资源优势，从而缩短计算时间。

4 数值算例

在广州超算“天河二号”计算机上开展了一系列测试，以验证本文所设计的并行计算方法的有效性。该超级计算机的主要配置请参阅2.2节。并行计算每次启动的结点机总数依次为50,100,150和200，实际参与并行计算的核数依次为9 750,19 500,29 250和39 000。

该异构超算上的每颗CPU有12个计算核心，每个MIC卡可使用57个计算核心，因此配置2颗CPU和3个MIC卡的结点内共有195个计算核心。“天河二号”CPU/MIC单结点内的协同并行加速测试表明，1个MIC卡的计算性能约相当于2路CPU的性能，即1CPU+1MIC可以达到1CPU计算速度的3倍。

4.1 并行计算数据准备

在并行计算开始前先进行两级分区处理。对于每个计算模型，一级剖分时产生的一级子区域总数应与每次参与并行计算的结点机总数相等，即应依次为50，100，150，200。由于“天河二号”每个结点机内配置5个计算设备(2颗CPU、3个MIC)，因此二级剖分时每个一级子区域被进一步剖分为5个二级子区域。

4.2 结构静力分析并行计算数值算例

结构静力分析并行计算的测试模型如图3所示，主要分析土木领域某盾构隧道模型在土体重力作用下的初始应变和应力。隧道主线长2 792 m，土层长2 000 m,宽300 m，深80 m。网格剖分采用四面体单元，该模型具有120 574 032个单元，23 379 547个节点。

结构静力分析并行计算的结果数据如表1所示。表1中，并行计算总时间从读取数据文件开始到计算各子区域应变/应力结束；缩聚时间指的是消去各子区域内部自由度所花费的时间、迭代求解时间包括求解界面方程的时间、回代内部自由度的时间和计算子区域应变和应力的时间。

Figure 3 Tunnel model for parallel computing图3 隧道计算模型

由表1可见，随着计算核数的增加，有限元结构静力分析并行计算的总时间依次减少，加速比呈现逐步增加的趋势。另据本文相关研究测试数据表明，与传统迭代计算方法相比，在使用19 500核时，本文方法总计算耗时只有前者的67%，并且总计算时间节省优势随着核数的增加不断扩大。

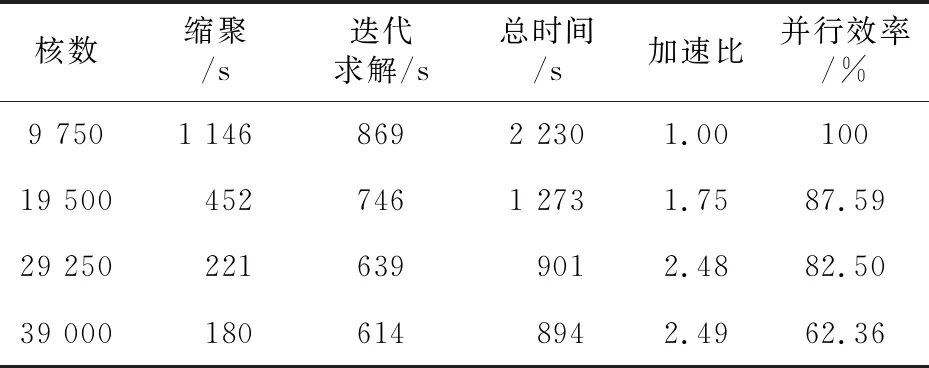
Table 1 Statistics of time and performance of parallel computing for static analysis表1 静力学并行计算时间和性能统计

由于本文设计的多层次多粒度协同并行计算方法不但实现了CPU设备和MIC设备间的负载均衡，而且显著节省了系统所需的通信开销，故能有效利用异构众核超级计算机的硬件资源获取较高的加速比和并行计算效率。

4.3 结构动力分析并行计算数值算例

结构动力分析并行计算的测试模型如图4所示，主要分析核电领域某防浪堤模型在地震载荷作用下的动力响应行为。防浪堤长2 280 m，土层长1 820 m，宽900 m，深350 m。网格剖分依然采用四面体单元，该模型具有113 492 512个单元，21 669 412个节点。动力分析的时间步长定为0.01 s，求解10 s，总计1 000个时间步。

结构动力分析并行计算的结果如表2所示。表2中，并行计算总时间从程序启动开始到所有时间步都计算完毕结束；缩聚时间指的是消去各子区域内部自由度所花费的时间、迭代求解是所有时间步的迭代求解时间的总和，每个时间步的迭代求解时间包括求解界面方程的时间、回代内部自由度的时间和计算子区域应变/应力的时间。

Figure 4 Breakwater model for parallel computing图4 防浪堤计算模型

Table 2 Statistics of time and performance of parallel computing for dynamic analysis表2 动力学并行计算时间和性能统计

由表2可见，利用多层次多粒度协同并行计算方法求解结构动力分析问题时，系统同样能够获取较高的加速比和并行计算效率。另据本文相关研究测试数据表明，与传统迭代计算方法相比，在使用19 500核时，本文方法总计算耗时只有前者的63%，并且总计算时间节省优势随着核数的增加不断扩大。

相对静力学分析而言，载荷均衡和最小化系统间的通信开销对动力学分析显得更加重要。这是由于动力学分析要对多个时间步进行求解，任何载荷分配的不均衡和通信效率的下降都会在多次求解中被放大，从而极大地影响到系统整体的并行计算效率。

结构动力分析并行计算需要对多个时间步依次求解，每个时间步都类似求解一次结构静力学问题。因此，结构动力分析时间步越多，所累计节省的绝对计算时间也越多，工程问题计算分析的效率提升优势也更为明显。

本文设计的多层次多粒度并行计算方法很好地解决了CPU设备和MIC设备间的负载均衡问题，对于大部分计算任务实现了多核和众核资源的协同并发执行。计算结果表明显著降低了在超级计算机上执行计算任务时所产生的通信开销，因而可以大大提高大规模结构动力分析的并行计算效率。

4.4 单机可扩展性测试

为评估核数一定时不同网格数量的计算规模对程序性能的影响，本文在单个结点机上进行了系统可扩展性测试。测试模型为左端固定右端受竖直载荷的悬臂梁，主要分析悬臂梁在静力载荷作用下的应变和应力。悬臂梁采用四面体单元进行网格剖分，通过不断加大计算网格的节点数和单元数测试系统在不同计算规模下的性能，得到的并行计算结果如表3所示。

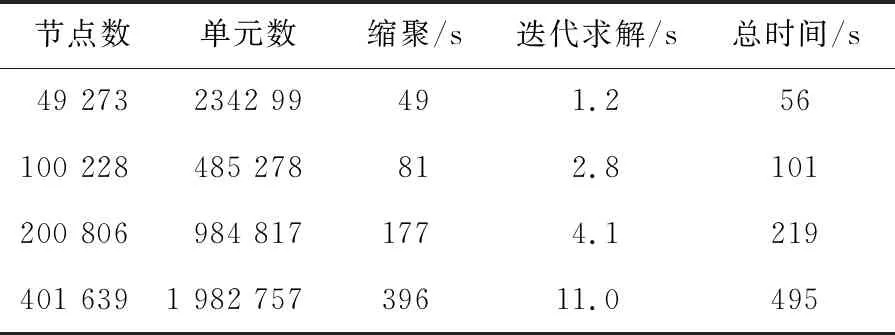
Table 3 Scalability test on a single machine表3 单机可扩展性测试

由表3可见，随着悬臂梁模型计算网格节点数和单元数的成倍增加，并行计算总时间也基本呈现出同样成倍增加的趋势，这表明本文方法在有限元规模扩大时具有良好的可扩展性。依据此趋势，在研究其他复杂工程问题时，可以从小规模计算模型建模调试入手，在此基础上继续扩大计算模型网格规模、调用更多计算结点，以获得更为准确的仿真计算结果。

5 结束语

为提高异构众核超算上有限元结构分析大规模并行计算的效率，设计了一种多层次多粒度协同并行计算方法。通过使每个计算作业被分解映射到异构超算的各硬件层面运行，在有效处理CPU与MIC之间的负载均衡问题的基础上显著降低了异构超算的通信成本。因此，它能够通过充分发挥超算系统的硬件资源规模优势来表现出最优的计算性能。

采用本文方法在“天河二号”超算系统上开展了几个有限元结构静力分析和动力分析所对应的的大规模并行计算数值算例的测试验证，启动的CPU+MIC核数总计达39 000个，分析的有限元规模超过1亿单元。测试结果表明，本文方法表现出良好的加速比和并行计算效率。未来计划将在新一代国产异构超级计算机上进一步开展测试和工程应用研究。