卸载型异常高压地层压力预测方法

张祯祥 杨进 孙挺 闫莉 张亦驰 欧启彬 李文拓

1. 中国石油大学(北京)；2. 武警后勤学院；3. 中海石油(中国)有限公司湛江分公司

南海乐东区域地处欧亚板块、太平洋板块和印澳板块的交汇处，高温高压特征显著，深部地层由于高温导致流体膨胀和生烃作用而产生异常高压，是典型的卸载型高压区域。乐东区域具有丰富的油气地质储量，精准预测地层压力是确保乐东区域油气资源安全高效开发的压舱石，不仅可以保障乐东区域油气资源的安全开采，同时也对其他卸载型高压区域的勘探开发具有借鉴意义，从而保障我国海上能源的安全供应。

地层压力精准预测面临诸多难题，传统的地层压力预测方法如 Eaton法［1］、等效深度法［2］、dc指数法［3-4］等，均是基于泥页岩的不平衡压实原理，不适用于不平衡压实以外的异常高压机制；对于比较复杂的地层无法获得真正连续的地层孔隙压力剖面，不适用非泥岩地层；正常压实趋势线的确定通常带有主观性，需要在实践中进行修正［5］；对于非连续沉积地层，通常需要建立多条正常压实趋势线，增加了趋势线确定的难度。

针对以上难题，国内外众多学者进行了相关研究。Bowers［6-7］基于流体膨胀产生的卸载型高压，针对泥页岩地层首次提出了考虑卸载机制的地层压力预测模型，但Bowers模型仅适用于泥页岩地层，没有考虑岩性、孔隙度因素对压力预测结果的影响。Han［8］基于砂泥岩石室内声波实验结果，指出影响砂泥岩声波波速的因素主要有孔隙度、泥质含量和有效应力。Eberhart［9］基于Han的室内分析结果，建立了考虑岩性、孔隙度和有效应力等因素的岩石声波波速经验模型，描述了孔隙度、泥质含量和有效应力对岩石中纵波波速的综合影响规律，但该方法没有考虑地层的异常高压成因机制。樊洪海［10］基于Eberhart建立的波速经验模型，得出了纵波波速经验模型的通解，并将纵波波速经验模型进行了推广，建立了利用测井资料预测地层压力的综合解释方法，但该方法也没有考虑地层的异常高压成因机制。目前缺乏一种结合卸载高压成因机制，同时考虑岩性、孔隙度和有效应力等因素影响的地层压力预测模型。

通过研究创建了一种针对卸载高压成因机制，同时考虑岩性、孔隙度和有效应力等因素影响的地层压力预测模型，解决了乐东区域卸载型异常高压预测精度较低的难题，同时也为其他卸载型高压区域的地层压力预测提供借鉴。通过开展室内声波测试实验，分别建立了声波波速与有效应力、岩性和泥质含量的函数关系。实验结果表明，声波波速与有效应力呈指数型关系，声波波速与孔隙度和泥质含量的平方根呈线性关系；然后利用线性叠加原理，建立了改进的Bowers地层压力预测模型。

1 模型建立

1.1 物理模型

乐东区域是典型的卸载型高压区域，由于地温梯度高，在深部地层产生流体膨胀和生烃作用，形成异常高压的卸载机制。根据乐东区域的异常高压成因机制，建立了卸载型高压的物理模型如图1所示。

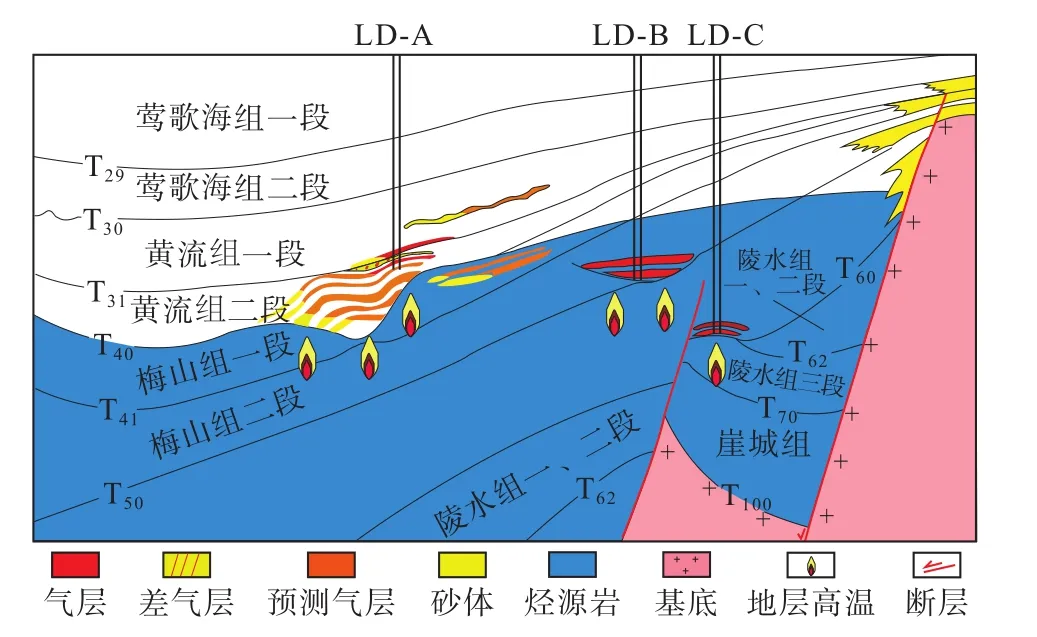
图1 乐东区域卸载机制高压物理模型Fig. 1 High-pressure physical model of the unloading mechanism in Ledong area

1.2 力学模型

根据图1中的物理模型，通过分析乐东区域的岩石微观孔隙结构，同时结合有效应力定理：地层压力与有效应力之和等于上覆压力，构建了乐东区域的地层压力力学分析模型。如图2所示，其中σ为上覆地层压力，MPa；p为地层压力，MPa；σev为垂直有效应力，MPa。

图2 地层压力力学模型Fig. 2 Mechanical model of formation pressure

1.3 数学模型

根据图2的力学模型，得出乐东区域卸载型高压的数学模型。其中地层压力等于上覆压力减去有效应力，通过构建岩石声波与有效应力的函数关系，间接求得地层压力。利用地层密度测井曲线，通过积分获得上覆地层压力为

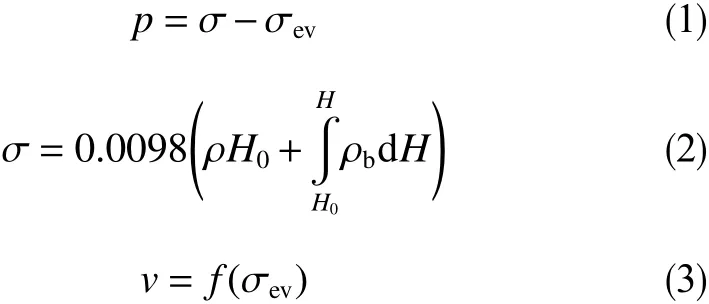
式中，ρ为上覆岩层的地层平均密度，g/cm3；H0为研究井段目的层的深度值，m；ρb为上覆岩层的地层测井密度，g/cm3；H为研究井段的起始深度，m；v为声波波速，m/s。

1.4 模型求解

模型研究中参考了乐东区域卸载成因段(井深4 000～4 100 m)的岩石强度特征、矿物组分和岩石物性参数(密度、孔隙度、渗透率、泥质含量)，制作含有不同孔隙度和泥质含量的砂泥岩人工岩心并开展室内声波测试实验，研究卸载机制下岩石声波波速与泥质含量、孔隙度和有效应力的关系。测试岩心均在氮气饱和情况下开展测试，同时均采用纵波测试。

(1)波速与有效应力的关系。分别选取2块不同孔隙度的砂岩岩心和2块泥质砂岩岩心，岩心A的孔隙度为5.6%，泥质含量为30.4%；岩心B的孔隙度为8.7%，泥质含量为12.8%；岩心C的孔隙度为8.9%，泥质含量为0%；岩心D的孔隙度为12.3%，泥质含量为0%。在围压70 MPa、垂向应力90 MPa、温度160 ℃下模拟地层温压条件，通过不断增加孔隙压力，使有效应力不断降低，观察岩石纵波波速与有效应力的变化规律，如图3所示。

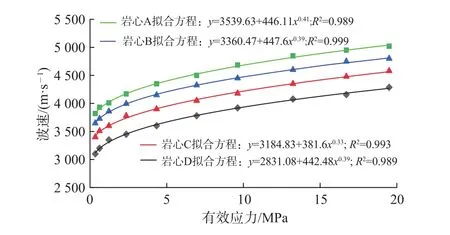
图3 波速与有效应力实验曲线Fig. 3 Relation between acoustic velocity and effective stress

根据测试结果可得，卸载机制下岩石声波波速随有效应力的降低而减小。分别将4块岩心的实验数据利用指数函数进行拟合，各曲线拟合效果较好，拟合系数均超过0.98。可以得出岩石声波波速与有效应力的函数关系为

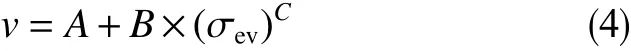
式中，A、B、C为相关系数，无因次。

(2)波速与孔隙度的关系。分别选取6块不同孔隙度的人工砂岩岩心，模拟地层温压条件(围压70 MPa，垂向应力 90 MPa，温度 160 ℃)，通过不断增加孔隙压力，使有效应力不断降低，观察卸载机制下岩石纵波波速与孔隙度的变化规律，如图4所示。

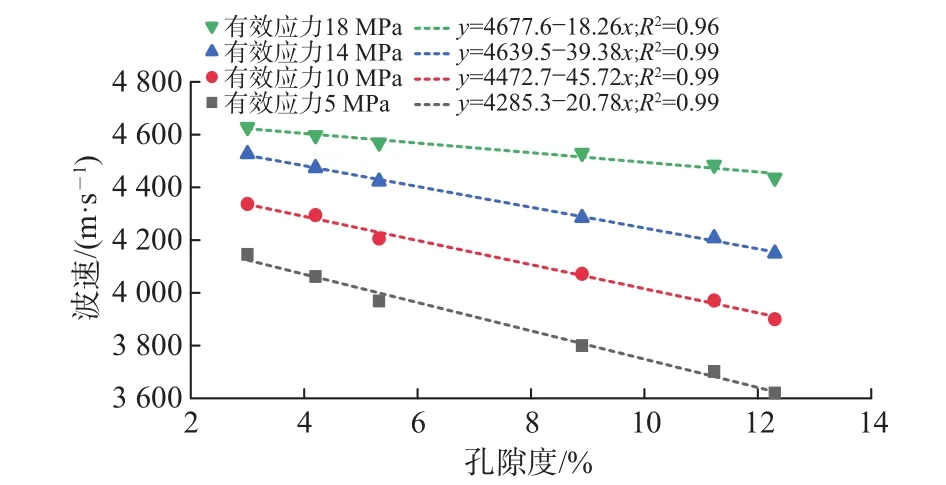
图4 波速与孔隙度实验曲线Fig. 4 Relation between acoustic velocity and porosity

通过测试结果可得，岩石声波波速与岩石孔隙度近似呈现出线性关系，声波波速随着岩石孔隙度的增加而线性降低，利用实验结果拟合出的函数关系为

式中，φ为孔隙度，%；D、E为相关系数，无因次。

(3)波速与泥质含量的关系。分别选取6块泥质含量不同，孔隙度相似的泥质砂岩人工岩心，模拟地层温压条件(围压70 MPa，垂向应力90 MPa，温度160 ℃)，通过不断增加孔隙压力，使有效应力不断降低，观察卸载机制下岩石纵波波速与泥质含量的变化规律，如图5所示。

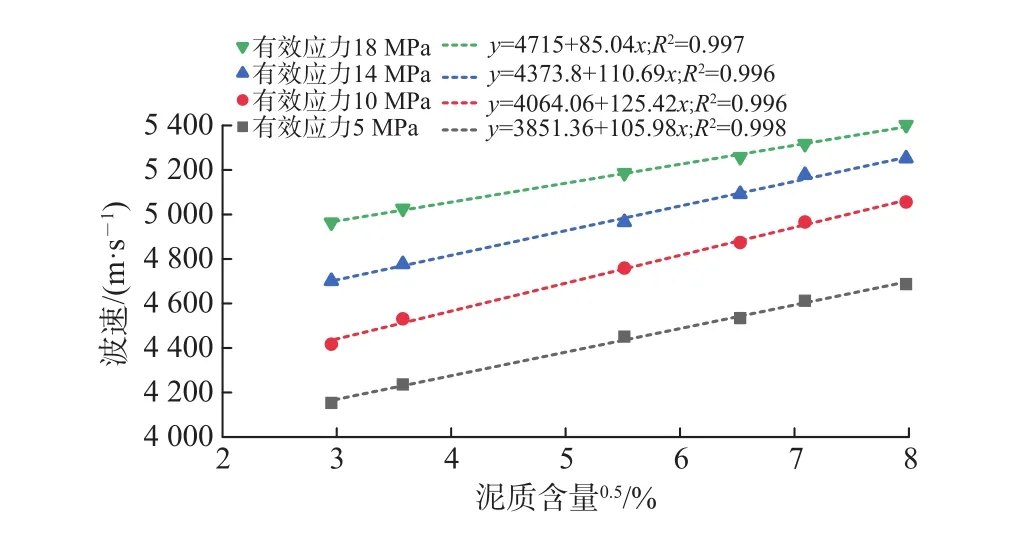
图5 波速与泥质含量实验曲线Fig. 5 Relation between acoustic velocity and shale content

通过测试结果可得，岩石声波波速与泥质含量的平方根近似呈现出线性关系，声波波速随着岩石泥质含量平方根的增加而线性增加，利用实验数据拟合出的函数关系为

式中，Vsh为泥质含量，%；F、G为相关系数，无因次。

利用线性叠加原理，得出声波波速与有效应力、孔隙度和泥质含量的函数方程为

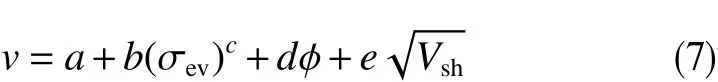
式中，a、b、c、d、e为相关系数，无因次。

2 结果讨论

2.1 改进Bowers模型克服了原始Bowers模型中对岩性的限制

原始Bowers模型中卸载方程的适用条件仅局限于泥页岩地层，模型中没有考虑岩性和孔隙度对声波波速的影响。改进Bowers模型综合考虑了有效应力、孔隙度和泥质含量对声波波速的影响，新模型中考虑的因素更加全面。原始Bowers模型的卸载方程为

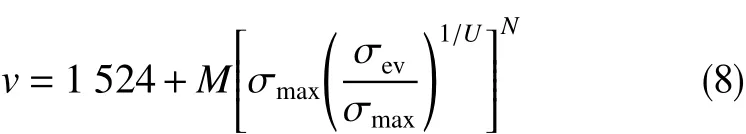
式中，σmax为卸载开始时的最大垂直有效应力，MPa；U为泥岩弹塑性系数，无因次；M、N为相关系数，无因次。

从2个模型的表达式中可以看出，式(8)中没有孔隙度和泥质含量，波速方程的影响因素只有有效应力和相关系数；而式(7)中，等式的右侧包含有效应力、孔隙度和泥质含量，同时还有相关系数。

2.2 改进Bowers模型解决了原始Bowers模型卸载方程中波速的理论缺陷

对于原始Bowers模型的卸载方程，当有效应力无限接近于0时，声波波速则是无限接近于海水波速1 524 m/s；而真实的地层压实情况为，当有效应力趋于0时，声波波速处于海水波速与开始卸载时的最大波速之间。如图6所示，当有效应力趋近于0时，两个模型的计算结果差距较大。改进Bowers模型得出的声波波速处于最大波速与海水波速之间，改进模型的计算结果更符合实际情况。

图6 改进的Bowers模型与原始Bowers模型对比Fig. 6 Comparison between the modified Bowers model and the original one

2.3 改进Bowers模型显著提高了地层压力预测精度

分别将改进Bowers模型的预测结果和原始Bowers模型的预测结果与乐东区域各井的地层压力实测值进行对比。如图7所示，改进Bowers模型预测结果的平均误差为2.6%，原始Bowers模型预测结果的平均误差为10.2%，改进Bowers模型的预测精度较高，满足现场要求。

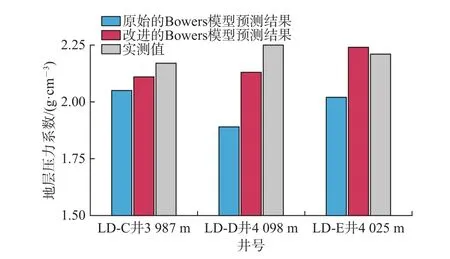
图7 改进的Bowers模型与原始Bowers模型预测结果对比Fig. 7 Comparison of prediction result between the modified Bowers model and the original one

3 结论

(1)通过室内声波测试分别得出了声波波速与有效应力、孔隙度和泥质含量的函数关系，构建了改进的Bowers地层压力预测模型，解决了乐东区域卸载型高压地层压力预测不准的难题，极大提高了乐东区域的地层压力预测精度，同时也为其他卸载型高压区域的地层压力预测提供指导。

(2)改进的Bowers地层压力预测模型中参数变量相对较多，预测精度对区域的依赖性较强，后续研究中应尽量搜集多口井的相关数据，扩充基础数据库，使得拟合出的地层压力预测模型的预测结果精度更高。