减载条件下刚性涵洞土压力计算方法
孟庆达,陈保国,王程鹏,闫腾飞
(中国地质大学(武汉) 工程学院,湖北 武汉 430074)
涵洞在公路和铁路建设中有着重要的地位,其应用非常广泛。现行的JTG D60-2015《公路桥涵设计通用规范》[1]采用“土柱法”计算涵顶土压力,但这种方法忽视了涵-土刚度差异引起的涵顶土压力集中,使得很多高填方涵洞的设计荷载小于实际所受的竖向土压力,造成涵洞病害。JTG/T D65-04-2007《公路涵洞设计细则》[2]和TB 10002-2017《铁路桥涵设计基本规范》[3]采用“集中系数法”计算涵顶土压力,该方法虽然考虑了涵顶应力集中现象,且简单易用,但仍未能清晰反映出涵洞荷载的传递机理。
关于涵顶竖向土压力的理论研究 ,国内外已取得了许多成果。Marston等[4]基于散体材料极限平衡法,得出了Marston公式。Spangler[5]在其基础上提出了等沉面的概念。曾国熙[6]考虑了填土粘聚力的影响,对Marston公式进行了修正。顾安全[7]将涵洞看作倒置在弹性地基上的刚性基础,类似于条形基础沉降计算的弹性半空间无限体假设,推得涵顶土压力计算式。郑俊杰等[8]基于顾安全模型,考虑了涵顶内外土柱之间的摩擦作用使得台背竖向土压力小于其上填土自重荷载,提出了修正后的顾安全公式。
在涵洞减载措施的理论和试验研究方面,王晓谋等[9,10]通过现场试验研究了采用EPS板、松砂及松土作为柔性材料的高填方拱涵的减载效果,并建立了减载条件下涵洞竖向土压力计算模型。McGuigan等[11,12]通过模型试验和数值模拟,比较了有无减载材料情况下单室涵洞和双室涵洞顶部、侧墙及底部的土压力情况。陈保国等[13,14]考虑涵洞两侧填土附加应力的影响推得减载条件下涵顶竖向土压力的计算式,并提出了一种新型的减载式涵洞,通过模型试验和数值模拟得到了其减载效果和受力特性。蒋承轩等[15]在此基础上通过模型试验和数值模拟,比较了该新型减载式涵洞在刚性和柔性两种地基条件下的受力特性。Bartlett等[16,17]分别以EPS和TDA为减载材料对地下管涵进行减载试验,试验证明二者对于涵顶竖向土压力的减载效果良好。Al-Naddaf等[18]对铺设EPS板后的涵洞进行加载试验,涵顶竖向土压力的试验结果与用Boussinesq解计算和Marston理论计算结果较为符合。但是现有的减载条件下涵洞土压力计算理论研究中只关注涵顶竖向土压力的减载效果,忽视了侧墙摩擦力在“涵-土”体系中的作用,从而未能准确反映出涵洞基底的受力状态。
鉴于此,本文提出了减载条件下涵洞荷载传递机理模型,考虑涵顶内、外土柱摩擦力和侧墙摩擦作用,推得减载条件下涵顶竖向土压力、涵侧摩擦力和基底压力的计算式,利用模型试验和数值模拟验证了该计算方法的正确性,并比较了非减载和减载条件下的基底压力。
1 减载条件下涵洞荷载传递机理
考虑涵洞侧墙与填土的摩擦作用,基于弹性条件建立减载条件下刚性涵洞工作性状的物理模型如图1所示。图中:M12,M11,M13和K12,K11,K13分别为涵洞上方和涵顶平面以上两侧填土的质量和刚度;M22,M21,M23和K22,K21,K23分别为涵洞质量、涵洞两侧填土的质量和刚度。M32,M31,M33和K32,K31,K33分别为涵洞地基和涵洞两侧地基的质量及其刚度;τ1表示涵顶内外土柱体之间的摩擦力;τ2表示涵洞侧墙和涵侧填土之间的摩擦力;KP为减载材料刚度。
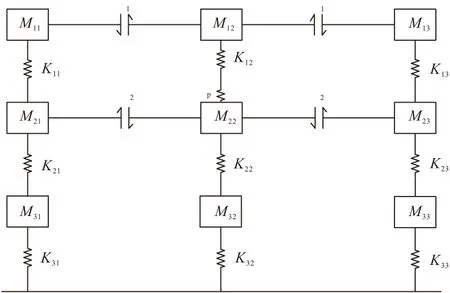
图1 减载条件下刚性涵洞作用机理
减载条件下,减载材料刚度Kp远小于填土刚度,使涵顶内土柱体等效刚度(Kp+K12)小于外土柱刚度K11和K13,内土柱M12沉降大于外土柱M11,M13沉降,涵顶内土柱体自重通过摩擦作用部分传递到涵侧土体,从而使涵顶土压力小于涵顶填土自重,达到减载效果。而涵侧土体产生附加应力,涵侧竖向土压力大于填土自重,产生“加载”的效果,同时造成涵侧水平土压力增大。由于涵侧填土和涵洞的刚度差异,涵洞侧墙受到涵侧土体向下的摩擦力。上述的附加应力通过侧墙摩擦作用施加在涵洞结构上,进而导致涵洞基底压力增加。
2 减载条件下涵洞土压力计算
2.1 涵顶土压力计算
以曾国熙的填埋式结构物土压力计算基本假定为出发点,假设涵顶平面上方的内、外土柱体中的竖向土压力均匀分布,且外土柱对内土柱的水平土压力为主动土压力[6],同时假定涵洞和地基均为刚性,计算模型如图2所示。
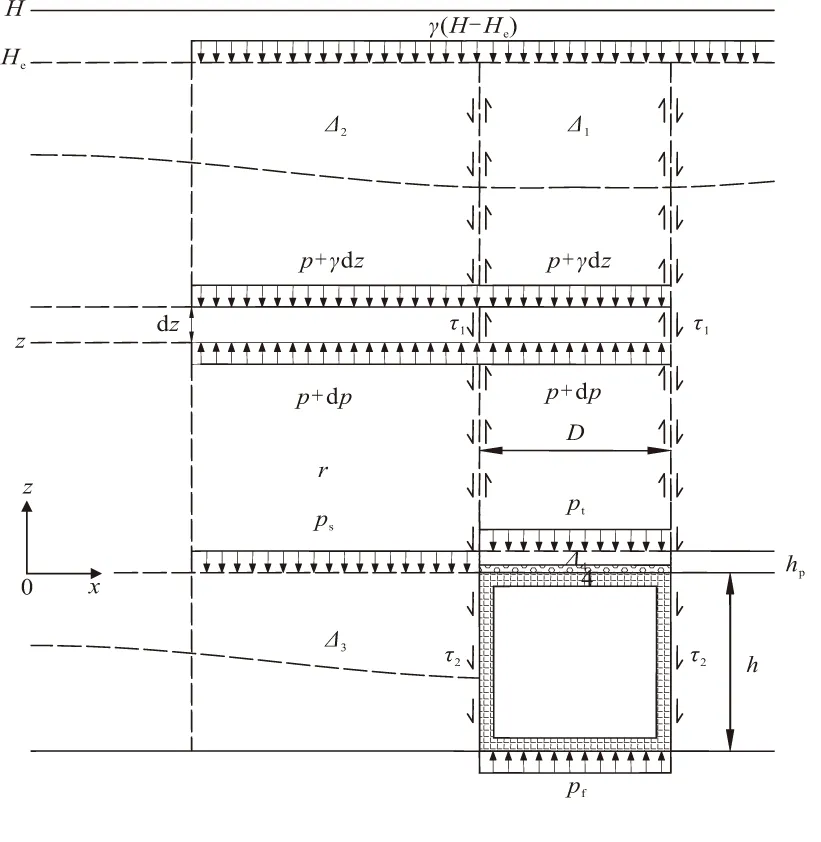
图2 理论模型示意
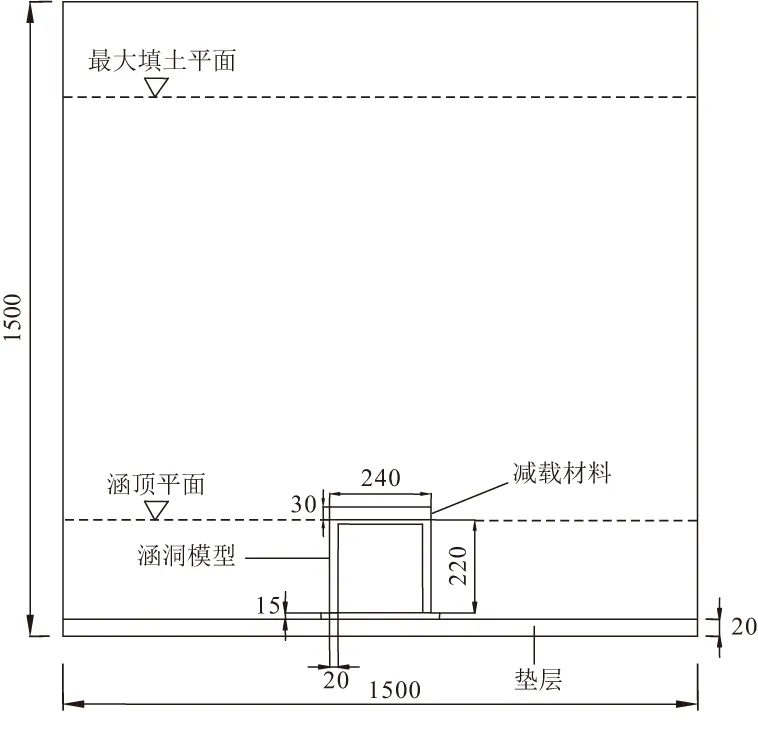
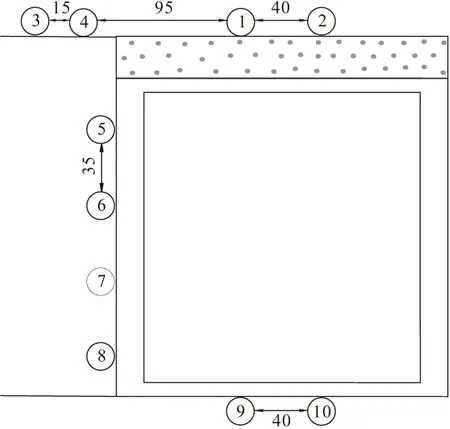
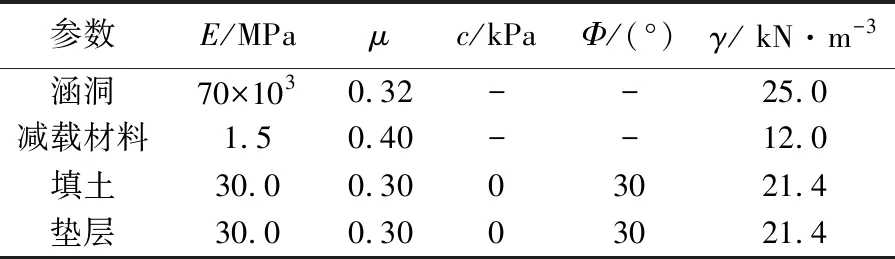
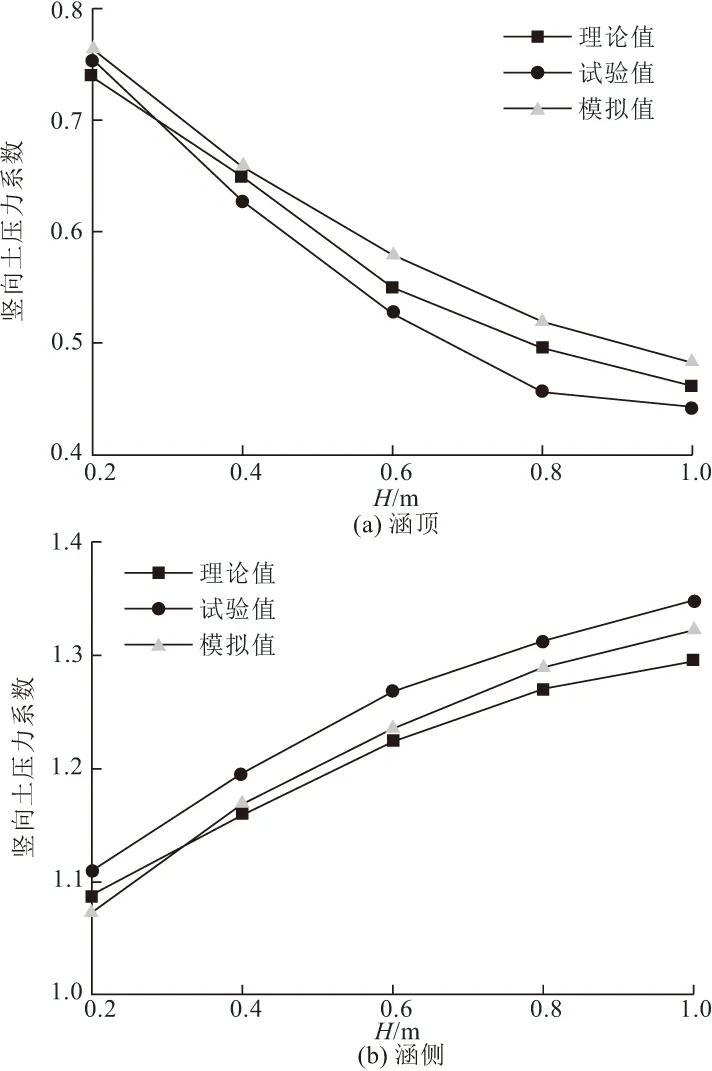
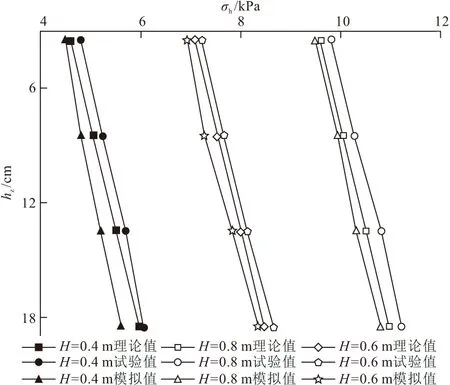
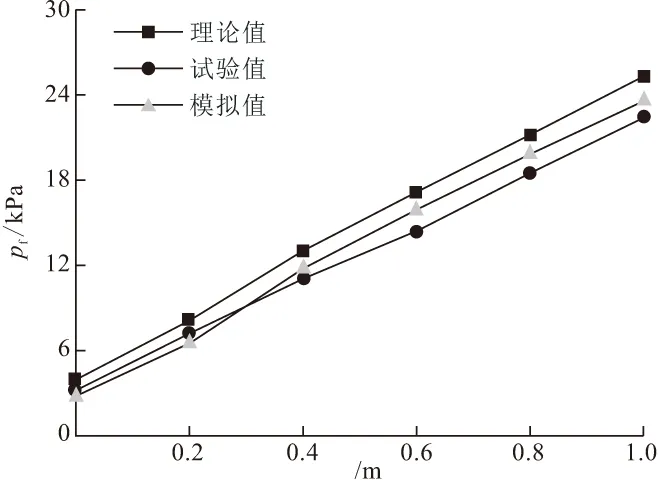
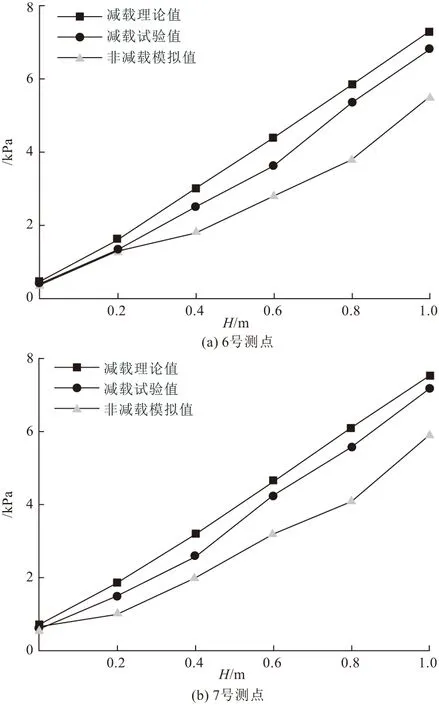
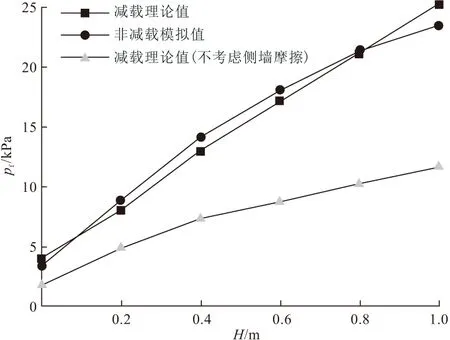
当填土高度大于等沉面(He),即H>He时,在涵洞上方内土柱中距涵顶平面z处(z (1) 对式(1)积分 (2) 可求得内土柱中距涵顶z高度处竖向土压力p(z)为: (3) 式中:B=fkγ。 减载材料的厚度较小,故忽略减载材料与土体的摩擦作用,同时不计减载材料重量。令式(3)中z=hp,则涵顶受到的竖向土压力pt为: (4) 式中:hp为减载材料厚度。 同理,在距涵顶平面z处(z (5) 式中:r为内对外土柱体摩擦力的影响范围,根据文献[8,13]可取r=D。 对式(5)积分 (6) 可求得外土柱中距涵顶平面z高度处(z (7) 令式(7)中z=0,可求得涵顶平面处外土柱体的竖向土压力为: (8) 当填土高度小于等沉面高度,即H (9) 可得减载材料顶面竖向土压力pt为: (10) 对式(5)积分 (11) 可得涵顶平面处,外土柱体的竖向土压力ps为: (12) 假设涵侧水平土压力成线性分布,侧墙水平土压力随涵侧深度的变化为: σh(z)=k0(ps+γkhz) (13) 式中:k0=μ/(1-μ),μ为填土的泊松比;hz为涵顶平面以下沿侧墙深度值。则涵侧摩擦力沿侧墙深度分布为: τ(z)=σh(z)f0 (14) 式中:f0=tanδ,δ为侧墙与填土之间摩擦角。 联立式(12)~(14)可得: τ(z)=μtanδ(ps+γkhz)/(1-μ) (15) 涵洞两侧受到的侧墙总摩擦力F为: (16) 涵洞的基底压力pf为: (17) 式中:L为涵洞长度;G为涵洞重力。 当填土高度达到等沉面以上时,内外土柱的沉降相等。即 Δ1+Δ4=Δ2+Δ3 (18) 式中:Δ1为等沉面以下内土柱的压缩变形量;Δ2为等沉面以下、涵顶平面以上外土柱的压缩变形量;Δ3为涵侧填土在侧墙高度范围内的压缩变形量;Δ4为减载材料的压缩变形量。 Δ1是由涵顶内土柱体的自重应力和外土柱体对内土柱体的附加摩擦作用引起的,Δ1为: (19) 式中:E为涵顶填土变形模量。 同理,Δ2可表示为: (20) Δ3可表示为: Δ3=(1-k0f0)(2ps+γkh)h/(2Ek) (21) 式中:Ek为涵洞高度范围内两侧填土的变形模量;γk为涵洞高度范围内两侧填土的重度。 不计减载材料自重和减载材料与外土柱体摩擦作用,则Δ4为: Δ4=pthp/Ep (22) 式中:Ep为减载材料变形模量。 将式(19)~(22)代入式(18),即可求出He。 试验模型如图3所示。模型箱的长、宽、高均为150 cm,涵洞高度为22 cm,宽24 cm,侧墙厚度2 cm。在模型箱内壁均匀涂蜡,使得内壁光滑,以此来减小模型箱内壁与填土的摩擦作用。模型试验的相似比为1∶30[14]。在涵顶、涵侧和基底共布设10只LY-350型应变式微型土压力盒,如图4所示。试验过程:将模型箱直接置于实验室混凝土地面,模型箱底面铺设2 cm砂垫层,找平压实,然后安置基底土压力盒。找平压实之后安装涵洞模型;在涵顶上方铺设EPS板,进行涵侧填砂,填砂过程中按照预定的密度称量相应的重量,并按照实验方案布设涵侧土压力盒。涵洞两侧填砂与EPS板顶面水平后,待5~10号土压力盒数据稳定后记录相应数据,然后在涵顶平面按设计要求铺设土压力盒。之后在涵洞顶部按照计算密度和称重逐级进行填砂,每级填砂高度为0.2 m,填砂结束后,待土压力监测数值稳定再进行下一次填砂,直至达到最大填砂高度1 m。 图3 模型试验示意/mm 图4 土压力盒布设/mm 涵洞模型使用铝合金材料制作,在涵洞侧墙外表均匀涂抹0.5 cm厚水泥砂浆,以模拟混凝土外墙。试验材料参数见表1。 表1 材料参数 采用有限差分软件FLAC 3D建立减载条件下涵洞模型。数值模型尺寸与模型试验一致。填土、垫层采用摩尔-库伦弹塑性材料,减载材料采用线弹性模型。填土和垫层采用实体单元,涵洞采用结构单元Liner模拟,以此反映侧墙与土体之间的接触关系和摩擦作用。模型四周约束水平位移,模型底部同时约束水平和竖向位移,不考虑排水固结的影响。数值模型剖面示意图如图5所示。 图5 数值模拟模型剖面示意 理论计算中,砂土与侧墙摩擦角可近似取墙侧填土内摩擦角[19],即δ=φ。表2为按本文理论计算得到的减载条件下涵顶竖向土压力pt、涵顶两侧填土竖向土压力ps和基底压力pf的结果。 表2 计算结果 涵顶竖向土压力系数和涵顶两侧填土的竖向土压力系数随涵顶填土高度的变化规律如图6所示。理论计算结果表明,减载条件下涵顶竖向土压力明显小于填土自重,且涵顶竖向土压力系数随填土高度增加而逐渐减小,最大填土高度时,涵顶土压力可减小至填土自重的45%左右。但涵顶两侧填土的竖向土压力大于填土自重,且该土压力系数随填土高度增大而逐渐增大,说明涵顶部分土压力通过内外土柱体的摩擦作用向两侧传递,达到涵顶“卸荷”目的,但该部分土压力对涵顶两侧填土起到了“加载”的作用。试验和数值模拟得到的竖向土压力系数变化规律与理论方法得到的规律相一致,数值上较为接近,数值模拟结果的最大误差在8%左右,试验结果的最大误差在9%左右。 图6 减载条件下竖向土压力系数随填土高度变化关系 不同填土高度时侧墙水平土压力沿侧墙的分布规律如图7所示。模型试验和数值模拟结果表明侧墙水平土压力近似呈线性增加,与文中理论计算结果相符。三种方法得出的涵洞基底压力变化规律如图8所示。基底压力随填土高度增加而逐渐增大,数值模拟和试验结果与理论方法得到的结果较为接近,误差低于10%。 图7 减载条件下侧墙水平土压力沿侧墙深度分布规律 图8 减载条件下基底压力随填土高度变化关系 根据本文提出的减载条件下涵洞荷载传递模型可知,非减载涵洞的基底压力由涵顶土压力、涵洞自重应力和考虑土压力集中的侧墙摩擦力三部分组成。而对于减载条件下的涵洞,其基底压力由卸载后涵顶土压力、涵洞自重应力和考虑涵侧填土附加应力增量的侧墙摩擦力三部分组成。由此可见,减载后的涵洞基底压力的大小并非由“卸荷”后涵顶竖向土压力决定。 为对比分析非减载和减载条件下涵洞基底压力,在本文的数值模型基础上建立非减载条件下(直接在涵顶填土,其余条件不变)涵洞模型进行数值模拟分析。 图9为减载和非减载条件下侧墙6号和7号测点的摩擦力随填土高度变化规律。结果表明两种条件下侧墙摩擦力均随填土高度的增加而增加,且减载条件下摩擦力的增长趋势明显高于非减载条件下,说明涵顶两侧填土的附加应力增大了涵侧填土对侧墙的摩擦力。 图9 侧墙6,7号测点摩擦力随填土高度变化关系 图10为基底压力随填土高度变化关系,由图可知,考虑侧墙摩擦作用时,非减载条件下基底压力随填土高度的变化规律与减载条件下的变化规律相同,且计算结果相差12%以内,表明减载措施未能减小涵洞的基底压力。若在减载理论计算中不考虑侧墙摩擦力,基底压力的计算值与实际值相差近2倍,说明侧墙摩擦作用在减载条件下对基底压力影响较大,在理论分析中不可忽略其对涵洞结构受力的影响。 图10 基底压力随填土高度变化关系 针对现有减载条件下涵洞土压力计算中未能考虑侧墙摩擦作用的问题,提出了减载条件下刚性涵洞荷载传递机理模型,推得涵洞土压力的计算式,并比较了非减载和减载条件下的基底压力,得出如下主要结论: (1)考虑涵顶内、外土柱摩擦力和侧墙摩擦作用,推得减载条件下刚性涵洞土压力计算方法,理论计算结果与模型试验和数值模拟结果接近,误差低于10%。 (2)减载与非减载条件下的涵洞基底压力均随填土高度的增加而增大,且二者结果接近,相差不超过12%。 (3)减载措施增加了侧墙摩擦力,若在减载条件下涵洞土压力计算中不考虑涵侧摩擦作用,得出的基底压力值将低于实际值近50%,给涵洞结构设计带来很大的安全隐患。
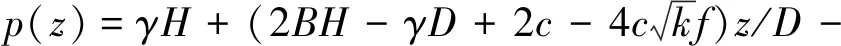
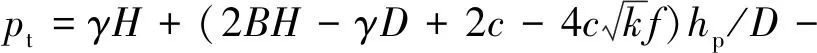

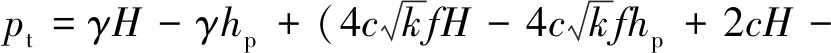
2.2 涵侧摩擦力计算
2.3 基底压力计算
2.4 等沉面的确定
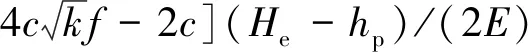
3 理论计算方法验证
3.1 模型试验
3.2 数值模拟
3.3 计算结果对比分析

4 基底压力
5 结 论

