织物接触冷暖感的模拟分析

蔡 彦，陈怡充，严航宇，杨允出

(1.浙江理工大学 服装学院，浙江 杭州 310018； 2.浙江理工大学 国际教育学院, 浙江 杭州 310018)

织物接触冷暖感指织物与皮肤接触时给人体皮肤的温度刺激在人们大脑中形成的关于冷或暖的判断[1]。长期以来，国内外学者对织物冷暖感进行了大量研究，目前较为成熟的实验测试方法是通过KES-F7型织物冷暖感测试仪测试的织物最大瞬态热通量qmax值[2]评价织物的接触冷暖感。国内在织物接触冷暖感的研究上起步较晚，但也有了大量相关研究，张旭靖等[3]对14种内衣织物进行比对测试，得到织物接触冷暖感与织物表面粗糙程度、织物含气量以及织物厚度的关系。俞涤美等[4]开发了一种凉爽型服用面料，并通过面料接触冷感、热传导等指标对其进行测评。董陈磊等[5]运用瞬态平面热源法对不同温度条件下织物的热导率进行了探究。张如全等[6]基于单片机开发了一台能模拟织物与人体皮肤接触时热交换过程的装置，用于评价织物接触冷暖感，实验证明该测试装置具有良好的精度。资菲菲等[7]运用反问题方法，提出了织物动态热湿传递数值模型中单层织物孔隙率的最优解。Tian等[8]以双层织物为对象，探究了织物厚度、织物堆积顺序和表皮结构等变量对瞬态最大热通量、稳态热通量等参数的影响。Itani等[9]在恒定热通量下用暖体假人对降温背心中相变材料在不同身体部位的最佳排列方式进行了探究，确定了不同躯干节段上相变材料包的最佳布局。上述对于织物接触冷暖感的研究，多基于实验仪器显示的单一物理指标对织物接触冷暖感进行评价，无法对织物与人体皮肤接触的过程进行表征。计算机模拟方法可通过建立几何模型进行仿真模拟，针对不同条件进行相应的模拟，为织物接触冷暖感的预测分析提供了方向。近年来，越来越多研究者采用计算机模拟方法研究织物舒适性，包括织物接触热阻[10]、织物接触人体后皮肤温度[11]以及空气层对多层织物传热的影响[12]。陈扬等[13]运用Ansys软件对非稳态条件下织物传热情况进行了模拟，但均未涉及织物接触冷暖感中的热通量值。

本文通过有限元仿真模拟的方式，对机织物接触冷暖感进行探究。通过分析织物与人体皮肤接触瞬间热量传导的情况，建立有限元仿真模型，通过实验验证模型的可靠性，并运用模型对毛羽层厚度变化及加入高热导率纱线时织物与人体皮肤接触面热通量的变化进行预测分析。

1 建立仿真模型

织物是由纱线、纱线间空气和纱线周围的毛羽共同组成的整体，内部纱线间存在众多孔隙，纱线的形态结构各不相同，因此影响织物接触冷暖感的因素众多，本文从组成织物的纱线层面进行探究，分析织物与人体皮肤接触时的热量传导过程，建立有限元仿真模型，对毛羽层厚度及织物内部纱线热导率变化的条件下进行模拟分析，探究这2种因素对织物接触冷暖感的影响。本文以机织物为主要研究对象，选取3种平纹织物进行仿真模拟。

1.1 建立织物几何模型

为建立织物三维几何模型，需要得到纱线的宽度、高度以及间距。用电子显微镜对织物进行测量，得到织物内部纱线的几何参数见表1。可以看出，纱线截面形态不是规则的圆形，为保证建立的模型中纱线更加真实，将纱线截面理想化的定义为椭圆形。

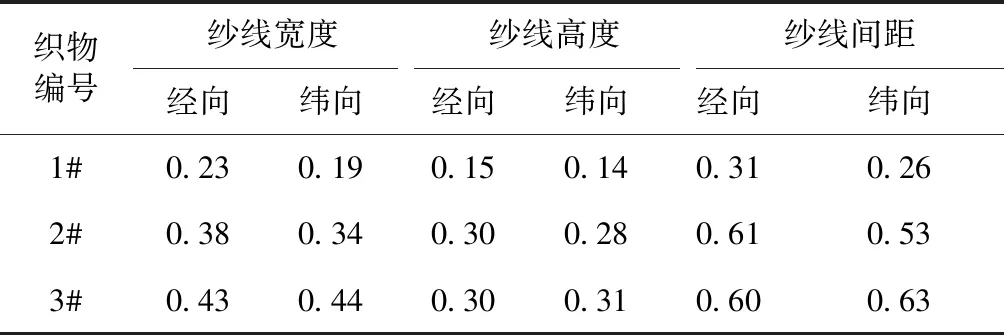
表1 织物内部纱线的几何参数 mm

运用Texgen软件进行建模，对纱线的截面形态与交织规律进行调整后导出模型，织物有限元模型见图1。可以看出，织物内部纱线周围的孔隙间存在大量毛羽，织物三维几何模型并不能表征出织物内部的毛羽。织物中的毛羽主要来自于纱线，纱线毛羽主要包括2类：生产过程中未被卷入纱线条干而外露的部分、生产过程中纱线表面附着的部分[14]。毛羽的存在会改变织物内部空间组成，影响织物接触冷暖感。为了简化问题，本文将织物内部毛羽与空气层视作一个复合材料的集合体。

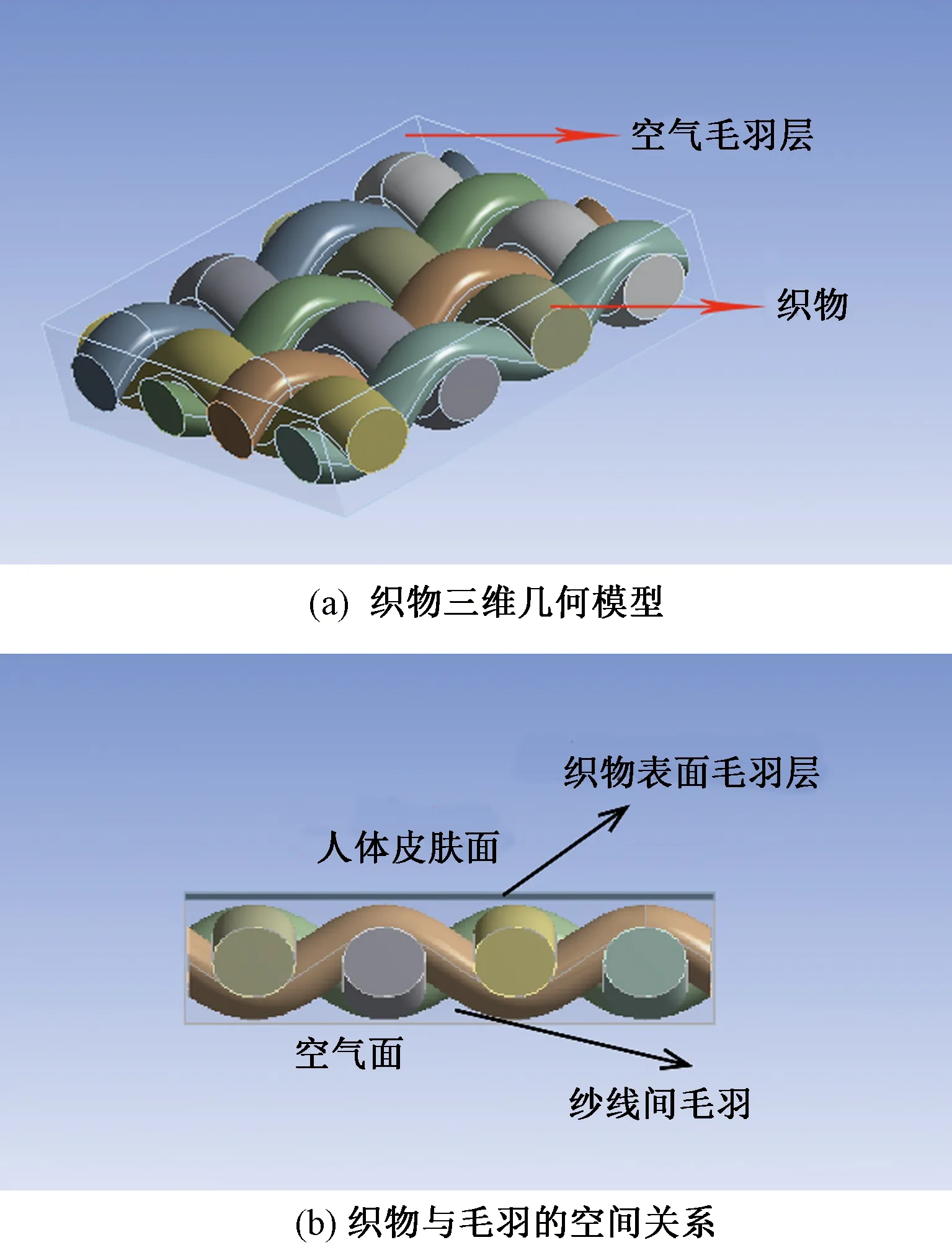
图1 织物有限元模型

1.2 毛羽层等效热导率模型

织物内部的毛羽形态大小具有随机性，无法准确测量。为研究方便，假设织物内毛羽与空气均匀分布。等效热导率可通过多相复合材料的多相层和平板式模型[15]进行计算，分别为两相串联模型和两相并联模型。等效热导率的串并联模型见图2。图中，q为热流量大小，W/m2；Va、V1为空气与毛羽层的体积占比，%；d、L1、L2分别为毛羽层厚度、空气等效宽度、毛羽等效宽度，mm。

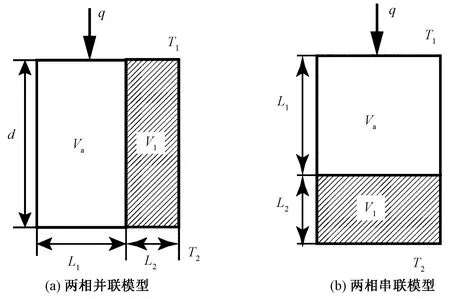
图2 等效热导率的串并联模型

假设织物内部毛羽层与空气层平行排列、所有毛羽热导率值均相等、热量传导方向与2种材料的交接面平行，等同于热导率串联。等效热导率的串联计算式见式(1)；热量传导方向与2种材料的接触界面垂直时，热量会依次通过2种材料，等同于热导率并联，等效热导率的串联计算式见式(2)。

(1)

(2)

式中：λm为等效热导率，W/(m·℃)；λa为空气热导率,W/(m·℃)；λ1为毛羽热导率，W/(m·℃)；V1为毛羽的体积占比，%。

由等效热导率的串并联模型可得，毛羽体积占比与毛羽热导率大小均为等效热导率的影响因素。传热方向与2种材料交接面平行时，毛羽等效热导率大小与其热导率大小以及体积占比均呈正相关；传热方向与2种材料交接面垂直时，纤维热导率和体积占比的增加均会使其等效热导率增大。

本文假定织物中毛羽体积占比为5%，空气的热导率从Ansys workbench软件数据库读取为0.024 2 W/(m·℃)，分别计算得到毛羽层集合体等效热导率，等效热导率串并联模型的计算结果见表2。

表2 等效热导率串并联模型的计算结果 W/(m·℃)

1.3 建立有限元模型

将三维几何模型导入Ansys workbench软件，对织物进行布尔运算，将织物设置为整体。因建立的模型只有纱线实体，纱线间为空腔，与织物实际不相符，故在纱线模型四周创建厚度为0.02 mm的包围层，用于表征织物内部除纱线以外的空气毛羽集合体。

建立织物模型并对织物模型中的材料参数进行设置，并进行网格划分与边界条件设定。本文模拟织物与人体皮肤接触瞬间织热量传导的情况，采用Steady-Thermal模块对这一瞬间的状态进行模拟。结合热通量qmax值得进行实验测试，定义织物模型上表面为与人体皮肤的接触面，上表面温度设定为30 ℃；定义织物模型下表面为与空气接触面，下表面温度设定为20 ℃，初始环境温度设定为20 ℃。假定织物四周边界为绝缘体，不与周边环境进行热量交换，仅在织物模型内部进行热量传导。

1.4 模拟预测分析

对毛羽层厚度变化以及加入高热导率纱线情况下，织物与人体皮肤接触面的热通量变化情况进行模拟预测分析。采用3#织物的4根经纱4根纬纱组成的平纹织物单元模型作为载体，针对毛羽层厚度以及加入高热导率纱线分别制定模拟方案。

毛羽层厚度变化会使得织物内部空气含量增多、整体厚度发生变化，从而影响织物接触冷暖感。为探究毛羽层厚度对织物接触冷暖感的影响，本文只针对与皮肤接触一侧的毛羽层进行研究，在纱线模型与人体皮肤接触一侧设置毛羽层。毛羽层厚度由0开始以0.02 mm为1个梯度依次递增至0.10 mm。

织物内加入高热导率纱线会影响织物等效热导率及织物接触冷暖感。由李丽[16]的研究可知，加入织物的纱线的热导率可高达0.504 5 W/(m·℃)，因此模拟中热导率取值从0.1 W/(m·℃)开始以0.05 W/(m·℃)为1个梯度递增至0.4 W/(m·℃)。

1根高热导率纱线位置示意图见图3。分别在织物中4根纬纱所在的4个位置(位置1、位置2、位置3、位置4)加入1根高热导率纱线，进行模拟。完成对单根高热导率纱线的模拟后，增加1根高热导率纱线进行模拟预测分析，2根高热导率纱线位置图见图4。

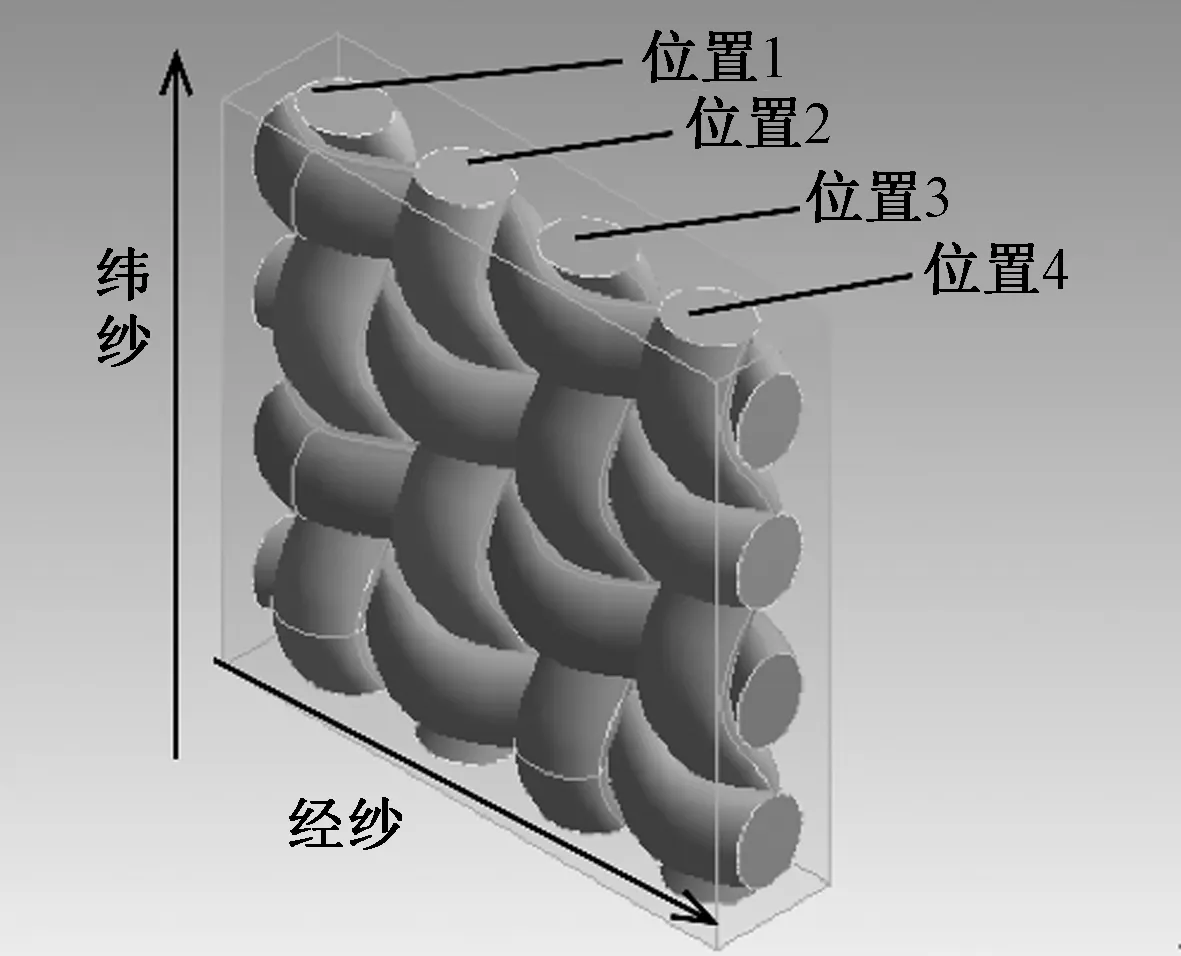
图3 高热导率纱线位置标注图

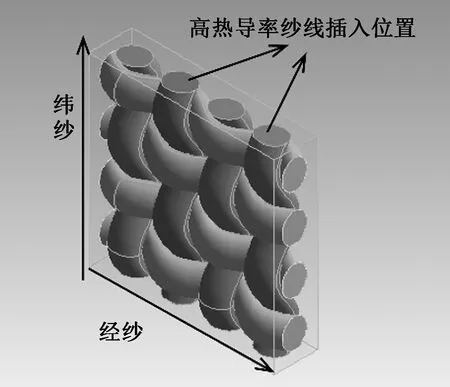
图4 2根高热导率纱线位置图

2 仿真模型验证

2.1 有限元模拟结果

运用Ansys workbench软件的稳态热传递模块进行传热分析，模拟织物与人体皮肤接触瞬间的热量传导情况。织物与人体皮肤接触面热通量模拟结果见图5。可以看出，热通量值差距较大，热通量最大值出现在织物交织点区域、最小值则出现在纱线间的空隙区域。在软件中选取最大结果输出，得到织物与人体皮肤接触面热通量结果为：1#织物为1 900.5 W/m2、2#织物为1 525 W/m2、3#织物为1 369.3 W/m2。

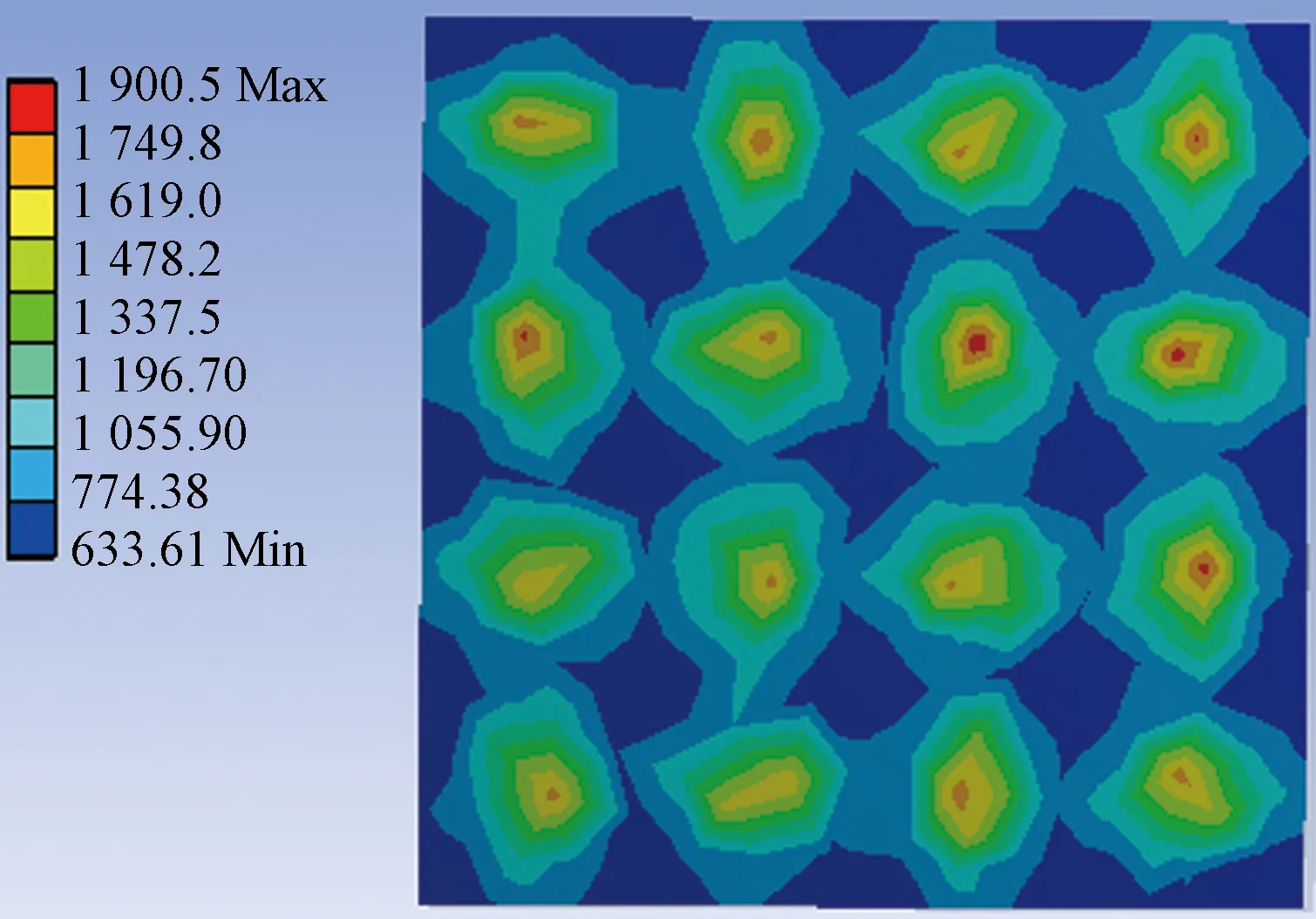
图5 织物与人体皮肤接触面热通量模拟结果

2.2 实验验证

对模拟结果进行验证，实验在恒温恒湿实验室(温度(20±2) ℃，相对湿度65%±5%)中进行。将KES-F7织物冷暖感测试仪的定温台Waterbox温度设定为20 ℃，BT-Box温度设定为30 ℃，待仪器稳定后对3种面料分别进行3次测试，读取热通量qmax值。将测试的热通量qmax平均值与有限元模拟所提取的最大热通量值进行对比，实验测试结果与模拟结果的对比见表3。

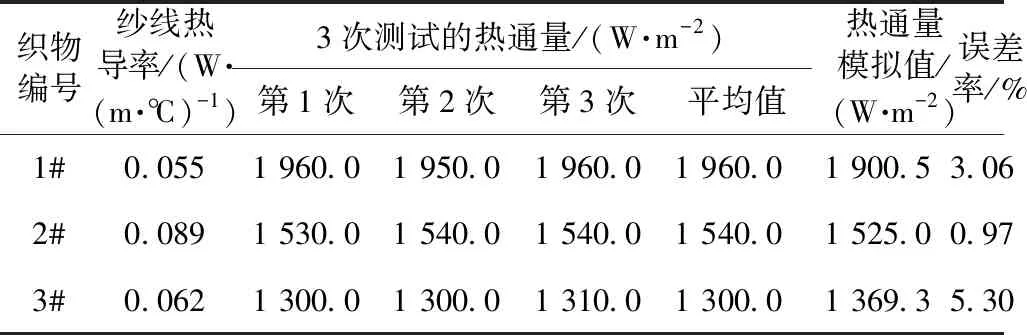
表3 实验测试结果与模拟结果的热通量对比

从表3可以看出，模拟结果与实验结果误差均小于6%，吻合度较好，本文建立的有限元仿真模型可用于评价织物接触冷暖感。

3 预测分析结果

3.1 织物毛羽层厚度对热通量的影响

织物内部普通纱线为纯棉纱线，模拟织物与人体皮肤接触瞬间热量传导情况，设置初始毛羽层参数，其中用于表征织物内纱线周围毛羽的包围层厚度与实验模拟相同为0.02 mm，施加载荷并求解。毛羽层厚度变化时热通量模拟结果见表4。毛羽层厚度变化时热通量模拟结果见图6。

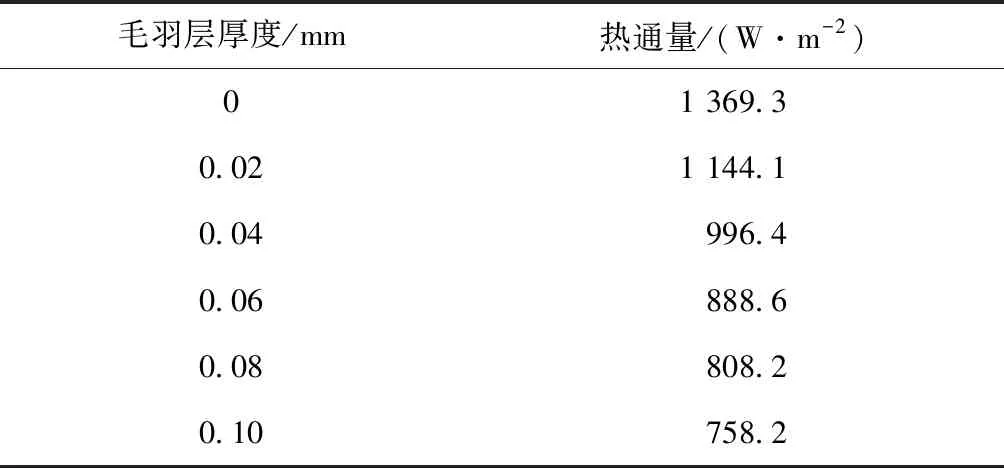
表4 毛羽层厚度变化时热通量模拟结果

图6 毛羽层厚度变化时热通量模拟结果

从图6可以看出，不同毛羽层厚度的织物与人体皮肤接触面热通量差别较大。热通量随毛羽层厚度增加逐渐减小，热通量越小织物能带走的热量越少，织物接触冷感觉越小。当毛羽层厚度增加时，织物厚度增加，与皮肤的接触面由纱线变为织物表面零散的毛羽。随着毛羽层厚度增大，织物与人体皮肤间间隙变大，织物整体厚度也随之变大，导致织物体积变大，使得织物中纱线体积占比减小，而空气体积占比增加，等效热导率减小，则织物与人体皮肤接触瞬间带走的热量减少，织物接触冷感觉降低暖感觉增强。

3.2 织物嵌入高热导率纱线对热通量的影响

织物内部普通纱线为纯棉纱线，模拟织物与人体皮肤接触瞬间热量传导情况，其中用于表征织物内纱线周围毛羽的包围层厚度与实验模拟相同为0.02 mm，设置高热导率纱线参数，施加载荷并求解。加入单根高热导率纱线时热通量模拟结果见表5。

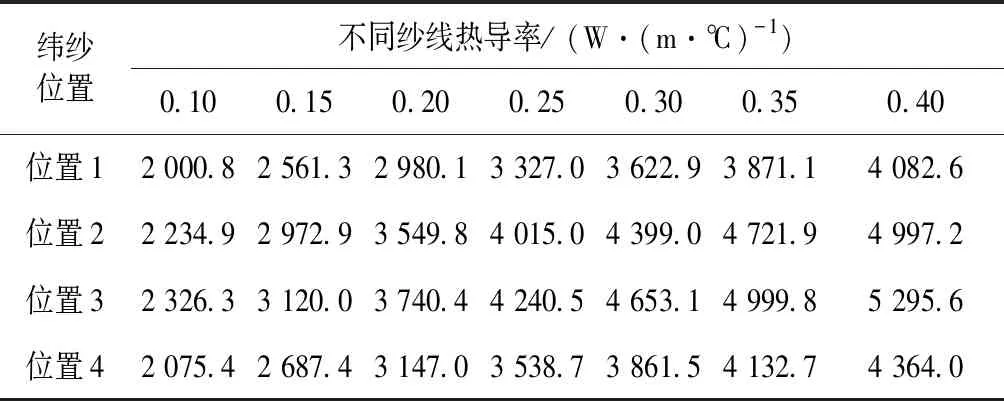
表5 加入单根高热导率纱线时热通量模拟结果 W/m2

当高热导率纱线的热导率变化时，通过织物与人体皮肤接触面的热通量变化明显。热通量随纱线热导率增加逐渐增加，相比于普通纯棉纱线，包含高热导率纱线的织物能带走更多热量，织物接触冷感觉越强。由表5可以看出，加入高热导率纱线时，织物与人体皮肤接触面热通量会随着纱线热导率增大而线性增大，且热导率越大热通量变化曲线越趋于平稳，其主要原因是加入高热导率纱线使织物等效热导率增大。根据等效热导率的串并联模型可得，织物等效热导率会随着高热导率纱线热导率增大而线性增大，热通量值也会随之线性增大。

将中间位置2、3的热通量值取均值，边缘的位置1、4热通量值取均值，高热导率纱线在织物中不同位置时的热通量结果见图7。由曲线分布可得，改变模型中高热导率纱线位置时，热通量值会发生变化。高热导率纱线位于位置1和位置4时，热通量值明显小于位置2和位置3。主要原因是预测分析中采用4根经纱4根纬纱组成的平纹织物，织物四周绝缘，不与外界发生热量传导，当高热导率纱线位于织物的不同位置时，其作用效果差异明显，从而引起热通量的差异。

图7 高热导率纱线在织物中不同位置时的热通量结果

其他条件不变情况下，改变高热导率纱线根数，由1根改变为2根，施加载荷并求解。改变高热导率纱线根数时热通量模拟结果见图8。

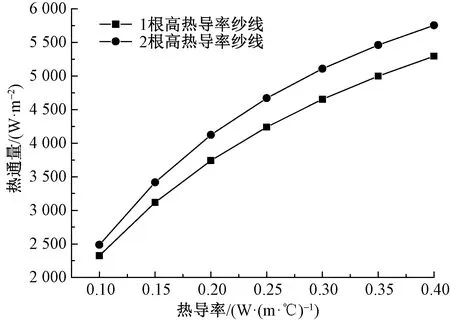
图8 改变高热导率纱线根数时热通量模拟结果

从图8可以看出，当高热导率纱线数量由1根变成2根时，通过织物与人体皮肤接触面的热通量值会有明显增大。根据等效热导率的串并联模型，当高热导率纱线数量增多时，高热导率纱线所占体积比增加，织物等效热导率增加，织物热通量也随之增大，织物接触冷感觉增强。

4 结 论

为了探究织物接触冷暖感，建立了三维模型，通过有限元软件，实现了对织物接触冷暖感的仿真模拟，结合实验验证了有限元模型的准确性。运用模型对毛羽层厚度变化以及织物中加入高热导率纱线时织物与人体皮肤接触面的热通量变化进行仿真模拟，得到以下结论。

①织物毛羽层厚度增加会使得热通量减小。毛羽层厚度增加，织物厚度也随之增大，织物整体等效热导率降低、热通量减小，织物接触冷感觉降低，因此增加织物表面毛羽层厚度可以有效降低织物接触冷感觉。

②织物中加入高热导率纱线时，热通量随着热导率增大而增大，且当热导率增大时热通量曲线增速趋缓。高热导率纱线的加入使得织物等效热导率上升，与人体皮肤接触瞬间能从人体皮肤带走更多热量，使得织物接触冷感觉上升。因此加入高热导率纱线是提高织物冷感觉的有效方法，且高热导率纱线数量越多，冷感觉提升效果越明显。