压力容器自增强技术的关键参数及其对自增强技术的影响
刘朝阳* 朱瑞林
(湖南师范大学工程与设计学院)
0 前言
压力容器自增强技术迄今仍是一种行之有效的确保安全、提高承载能力的方法。理论上,影响自增强技术效果的参数很多,且相互制约、相互影响。为了更有效地实施自增强技术,研究参变量对自增强技术的影响是必要的。通常认为,对于自增强容器,弹塑性界面处总应力的当量应力是危险的,必须加以限制,确定最佳弹塑性界面半径往往也是通过寻找弹塑性界面处最小总应力而获得[1-3]。这个观点具有实用意义,也在工程应用中起了很好的指导作用。但研究证明,自增强处理时施加的压力太大,会对设备产生不利影响[4-5]。而自增强压力的大小直接影响塑性区的深度(超应变度),超应变度的大小又影响着设备承载能力。因此在研究自增强压力和承载能力的问题时,有必要同时考虑弹塑性界面处总应力的当量应力和卸除自增强压力后筒体内壁面上的残余应力。
本文基于第三强度理论,同时假定:(1)容器材料是完全弹塑性的,包辛格(Bauschinger)效应忽略不计,压缩屈服强度等于拉伸屈服强度;(2)不考虑应变硬化;(3)材料没有缺陷。实际使用材料不同时可在本文的结果上加以修正。
1 基于控制弹塑性界面处总应力讨论



图1图像


2 反向(压缩)屈服问题
当k≥kc时,为了防止施行自增强处理时容器内壁面残余应力ei′超过强度极限y,在式(13)中令x=1 得ei′,再令ei′≥y可得:




表1 和 的数值解(k≥kc)
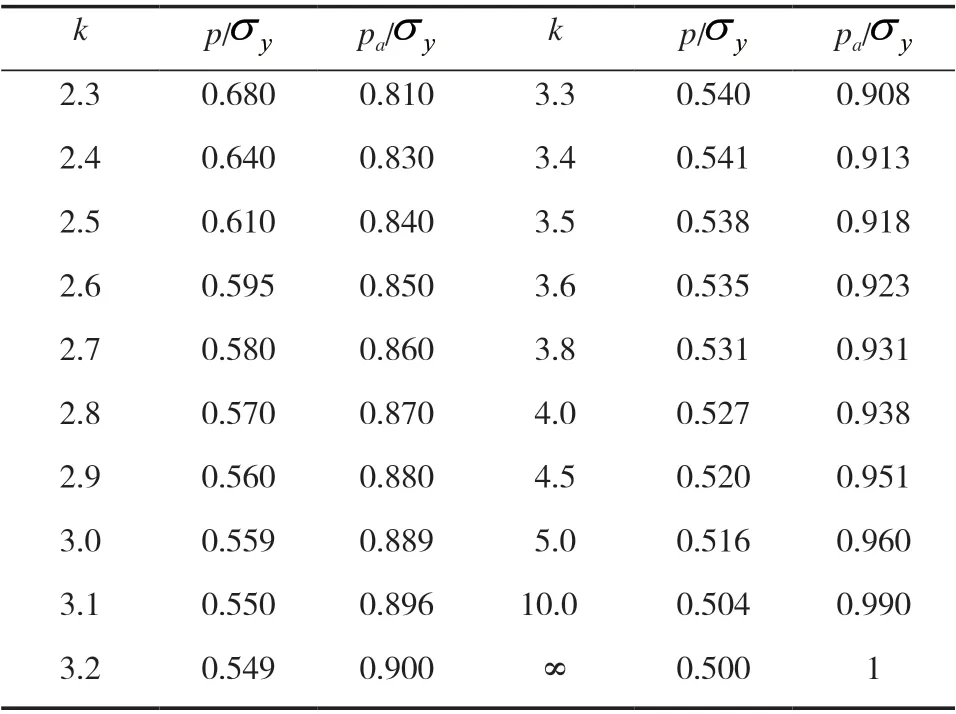
表1 和 的数值解(k≥kc)
k p/ pa/ k p/ pa/2.3 0.680 0.810 3.3 0.540 0.908 2.4 0.640 0.830 3.4 0.541 0.913 2.5 0.610 0.840 3.5 0.538 0.918 2.6 0.595 0.850 3.6 0.535 0.923 2.7 0.580 0.860 3.8 0.531 0.931 2.8 0.570 0.870 4.0 0.527 0.938 2.9 0.560 0.880 4.5 0.520 0.951 3.0 0.559 0.889 5.0 0.516 0.960 3.1 0.550 0.896 10.0 0.504 0.990 3.20.5490.900∞0.5001


图2 曲线

k≤kc时,式(22)所表达的曲线的端点位于直线ao 上,在该直线上有pa=p。因此直线ao 与横轴或纵轴的夹角是45°。
在图2 中,虚线没有实际意义,仅仅是实线的延长,即仅仅是式(22)所表达的数学关系的延伸。
3 结论




