基于Delaunay算法含定解条件的三角单元网格生成

宋小鹏 古小敏 何秀锦 吴国珊 王斌武

（桂林航天工业学院能源与建筑环境学院， 广西 桂林 541004）

摘  要： 有限元分析过程中，网格剖分除了要对计算域进行剖分，也要对网格单元的定解条件进行标识。文章探讨用Delaunay算法对二维计算域进行剖分，并生成包含定解条件（边界条件和材料属性等）的三角网格单元。对复杂几何图形采用分块策略，将计算域分为若干凸多边形，并对网格质量进行评估。以二维扩散方程为例，使用该算法生成的三角单元网格求解Laplace偏微分方程，计算结果与解析解吻合较好，表明该算法能够生成较高质量的网格单元。

关键词： Delaunay算法; 网格生成; 有限元; 定解条件

中图分类号：TP301.6          文献标识码：A     文章编号：1006-8228（2020）12-29-04

Abstract： In the process of finite element analysis， in addition to generating mesh for the computational domain， it is necessary to identify the solvability conditions of the mesh. Delaunay algorithm has been used to divide the two-dimensional computational domain and generate triangular mesh elements with solvability conditions （boundary conditions， material properties， etc.）. The complex computational domain is divided into several convex polygons， and the mesh quality is also calculated. Taking the two-dimensional diffusion problem as an example， the triangular element mesh has been generated using the Delaunay algorithm， and the Laplace partial differential equation has been solved. The numerical results are in good agreement with the analytical solution， which shows that the algorithm can generate high-quality mesh elements.

Key words： Delaunay algorithm; mesh generation; finite element method; solvability condition

0 引言

Delaunay三角化算法被廣泛用于有限元分析，很多学者对其算法做了大量研究：刘琴琴[1]对比了几个平面域Delaunay三角网生成算法，并做了改进工作;冯斌斌[2]等改进了Delaunay三角网格的生成方法，可自适应加密从而提高有限元计算精度;张晶飞[3]等讨论了基于Delaunay三角化的最优化网格节点生成算法。

很多学者对基于Delaunay算法的网格剖分算法进行了改进：李建平[4]等利用点角对Delaunay三角网格生成算法进行改进，提高了效率;陈明晶[5]等提出一种改进的Delaunay三角网生成算法，通过建立新的几何拓扑关系提高网格生成效率;青文星[6]等提出了结合逐点和分治的快速Delaunay三角网格生成的方法。Gmsh[7]是一款开源网格剖分工具，可对2D/3D计算域进行网格剖分，但是该软件目前并没有支持直接生成边界条件信息，如使用Gmsh生成的网格进行有限元分析，九需要额外的计算工作量指定边界条件和材料信息。本文基于Delaunay算法，对计算域进行三角单元剖分，对计算域分块，以支持对凹多边形网格剖分，并在剖分过程直接生成边界条件和材料信息，以便后期有限元计算使用。

1 基于Delaunay三角化的三角单元网格剖分

1.1 Delaunay三角化算法

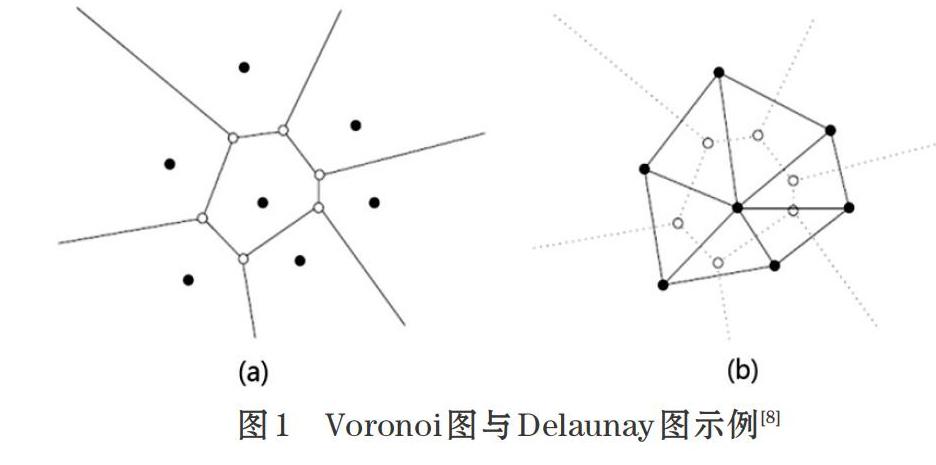
对于二维平面内的点集[S]内的[p]点，存在一个区域，使得任意一个[S]点集内的[q]点到平面上任意一点[x]的距离都不小于[x]点到[p]点的距离，那么，该区域称为点[p]的Voronoi区域，如图1（a）。根据参考文献[8] ，无限大二维平面Voronoi区域的定义为：

Voronoi图是点集内所有点的Voronoi区域合集，也是由所有相邻点构成的线段的垂直平分线所组成的连续多边形集合。Delaunay图是Voronoi图的对偶图，被中垂线分割的线段所组成的三角单元系列即为Delaunay图，如图1（b）。由点集生成Delaunay三角单元系列（普通三角单元不一定是Delaunay三角单元）的算法称为Delaunay三角剖分算法。

Delaunay算法[8]可以将点集三角化，主要有“局部变换法”与“增量算法”，其中Bowyer-Watson算法是一种“增量算法”，步骤为：①构造一个包含所有点集在内的超级三角形（super triangle），该三角形既第一个剖分出来的三角单元;②将离散点逐个插入，查找包含该点的所有三角形的外接圆，标记这些三角单元;③删除第②步中所标记的三角单元，连接插入点与第②步中标记的三角单元节点，形成新的三角单元;④插入其他新点，执行步骤②和③，直到插入所有点;⑤删除超级三角形及其边。