求取环氧树脂复合绝缘活化能的改进介电谱法

张 蔚，任 鹏，彭 鹏，黄旭炜，李庆民

（华北电力大学 新能源电力系统国家重点实验室，北京 102206）

0 引言

绝缘缺陷是造成电力设备故障的主要原因之一。目前电气设备绝缘监测的主要方法有局部放电检测法[1]、六氟化硫分解产物法[2]、紫外测量法[3]、溶解气体分析法[4]、高频脉冲震荡法[5]和介电检测法[6-9]，这些方法多是基于外部响应和宏观特征实现对绝缘缺陷和内部故障的检测。为提高检测的有效性，研究者也在探索基于微观特征量的绝缘缺陷检测方法。活化能通过表征电介质微观运动单元（电子、原子、分子、偶极子、界面等）的极化、弛豫及共振机制，描述了运动单元运动时需克服的能量势垒，是对绝缘老化状态的微观本征反映。

基于活化能表征绝缘材料的研究已取得了许多进展。廖瑞金等[10]对油浸纸板开展介电谱实验，获得老化程度与电容、体积电导率、介质损耗因数、相对介电常数之间的关联规律，并采用频-温平移因子求解活化能；张明泽等[11]分析了不同老化状态绝缘油的活化能，并辅以绝缘纸板聚合度和绝缘油酸值等测试，构建了绝缘寿命预测关系式。基于介电谱求取活化能，应用最广的是文献[10]提出的频-温平移法。此方法的理论基础是时温等效原理，即对于高分子材料的力学状态转变与力学松弛性能而言，外力作用时间和环境温度的影响具有等效作用。在某一频率外力的作用下，达到同一程度力学状态的时间随着温度升高而缩短，反映在表达力学状态随外力频率变化的曲线上，即曲线向高频方向移动。需要说明，时温等效原理描述了材料的力学性能松弛规律，对处于某一松弛力学状态的电介质而言，则在该种特征松弛时间内符合上述规律。

但在频-温平移法的实际应用中，出现了许多并不满足时温等效原理的物理场景，从而导致所求活化能差别较大。文献[12]将不同温度下的tanδ曲线平移到主曲线时，发现在f≤e0Hz频段的曲线不重合，这是因为tanδ在该频段内并不能反映实际弛豫过程的物理机制；文献[13]也因存在材料力学状态改变的温度临界点，引起了新的松弛现象，介电谱曲线不再反映单一的松弛过程，无法获得重合的平移曲线；文献[14]的研究表明，实际的介电谱曲线并不在全频段平移重合，只能对单一弛豫过程或者温度特性一致的多弛豫过程获得重合的平移曲线。本课题组在前期测试研究中发现，环氧树脂绝缘材料的介电谱曲线随温度升高在向右平移的同时有向上漂移的趋势，呈现“温漂”现象。材料的ε″曲线随温度升高漂移明显，仅沿频率轴平移难以获得重合主曲线。老化会使介电谱曲线的“温漂”现象更为严重，更加难以通过频-温平移法获得准确的活化能。

造成上述问题的原因，主要在于频-温平移法的应用场景和适用条件不甚明确，导致求得的活化能物理内涵不清，也难以与绝缘材料的具体弛豫过程建立物理联系。为此，本文通过深入分析“频-温平移法”的理论基础，进一步明确其适用物理条件和具体使用方法；同时，针对绝缘材料介电谱曲线出现的“温漂”现象，提出一种求取活化能的改进介电谱法，拓展“频-温平移法”的应用范围，使求取的活化能更为精确。

1 频-温平移法适用条件与存在的问题

1.1 频-温平移法的适用条件

根据双势阱模型描述的凝聚态电介质中微观运动单元的越障运动，可得到介电弛豫衰减函数，如式（1）所示。

式（1）中：τ为弛豫时间；ω0为运动单元在势阱中的振动角频率；Ea为运动单元运动时需要克服的势垒，称为松弛活化能；k为Boltzmann常数；T为热力学温度。

系统中可能存在不止一种类型的双势阱，而不同的弛豫对应不同的弛豫时间τ，随着温度升高，τ呈指数减小。电介质的介电响应有两种基本类型[15]，一种是由偶极子主导的介电响应[16]，另一种是由载流子主导的介电响应[17]。偶极子主导的介电响应在介质损耗曲线中有弛豫峰出现，当频率满足ωτ=1时则为这种松弛的特征频率；而载流子主导的介电响应过程没有弛豫峰，也称为低频弥散现象，这种松弛发生的频率区间满足ωτ≈1。

在某种弛豫占主导地位的特征频段，可把温度对弛豫时间（τ）的影响映射到温度对特征频段的影响上，即τ≈1/ω=1/(2πf)。大量实验数据表明，在电介质微观结构没有出现明显变化的温度范围内，介电谱曲线的形状变化很小，因此，由不同温度下介电谱曲线的平移量和温度的关系可以获得该弛豫类型的松弛活化能。若定义f0表示温度为T0时介电谱曲线某点平移前对应的频率，f表示平移后该点在温度为T时介电谱曲线上对应的频率，则从式（1）可推得式（2）。

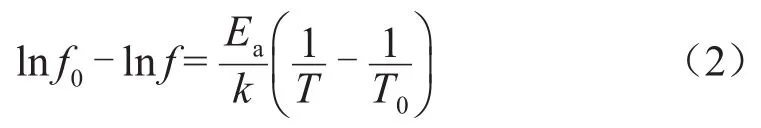
实测获得介电特性的频率谱和温度谱曲线后，由式（2）可拟合（lnf0-lnf）与(1/T-1/T0)的关系，其斜率即为Ea/k，从而求出活化能。

频-温平移公式的使用，需要首先明确几个关键物理量以及公式的适用条件：

（1）平移处理的物理量：介电谱曲线的物理量包括复相对介电常数的实部（ε′）和虚部（ε″），以及计算得到的介质损耗因数 tanδ=ε″/ε′等物理量。实部（ε′）反映介电响应过程中电荷的储存特性，而虚部（ε″）反映的是介电响应过程中的能量损耗，包括电导损耗和极化损耗，tanδ则是介质损耗中有功损耗和无功损耗的比值。鉴于介电谱曲线的平移是基于温度与弛豫时间的关联关系，平移物理量应能单纯表征主介电弛豫过程随频率变化的响应曲线，而其他响应过程的影响则可以忽略。

（2）可平移的频段范围：介电谱曲线应主要来自于起主导作用的单一弛豫类型，且在该弛豫类型的特征频段附近，满足ωτ≈1。若介电响应过程同时出现两种以上的主导弛豫类型，因温度对不同弛豫类型的影响各异，沿频率轴平移后未必能获得相重合的介电谱曲线。

1.2 频-温平移法的主要问题

为获得环氧树脂的活化能，本研究对环氧树脂试样（含有Al2O3填料、酸酐类固化剂的双酚A型E51环氧树脂复合绝缘材料）的介电谱测量进行实验，测量频段为10-3～103Hz，测量温度为30～100℃，间隔10℃，获得的介电谱曲线如图1所示。环氧树脂绝缘材料的制备过程包括恒温固化阶段，但固化温度一般高于100℃，固化时间一般大于16 h[18]，而本研究的测量温度低于固化温度，且在各温度下的测量时间小于20 min，故可忽略固化反应对求取活化能的影响。将图1沿频率轴平移不同温度的曲线，得到图2。从图1～2可以看出，ε′、ε″曲线随着温度升高向右平移，但同时有向上漂移的趋势。在利用频-温平移法分析介电谱曲线求取活化能时，沿频率轴平移不同温度的ε′曲线无法获得重合主曲线，ε″曲线的极小值点随温度上升而上升，亦无法获得重合曲线。由于tanδ=ε″/ε′，实验发现tanδ曲线的极小值点随温度变化现象与ε″曲线类似。这种介电谱曲线随着温度升高呈现向右平移的同时向上漂移的现象，称为介电谱曲线的“温漂”现象。

图1 环氧树脂试样的介电谱曲线随温度和频率的变化Fig.1 Dielectric spectra curves of epoxy resin samples with temperature and frequency

文献[19]测量发现发电机主绝缘的介电谱曲线也出现随着温度升高，整个频域曲线整体上移的现象。实验还发现老化会加剧这一现象，使介电谱曲线无法沿频率轴平移重合，导致无法获得平移量与温度的可靠关系，进而影响活化能的求取。

图2 环氧树脂介电谱曲线的平移结果Fig.2 Translation results of dielectric spectra curves for epoxy resin

1.3 “温漂”现象的物理机制

绝缘材料的介电弛豫过程主要有电子式极化、离子式极化、偶极子转向极化，而本文研究对象环氧树脂复合绝缘材料还存在夹层界面极化。温度升高会使极化的进行速度加快，弛豫时间减小，如文献[13]中环氧树脂介电谱曲线的峰1对应环氧树脂的b弛豫过程，属于偶极子主导的弛豫类型，随着温度升高向高频方向移动，如图3所示。介电谱曲线是由多个弛豫过程共同组成的，不同弛豫过程有其占主导的特征频段。电介质材料的转向极化多存在于e-4.6～e23Hz，界面极化多存在于f≤e-2.3Hz[20]。不同的弛豫过程在整个频段上彼此叠加，且每个弛豫过程的物理机理以及参与弛豫的运动单元不同，温度特性亦不同，所以存在多个弛豫过程的硅橡胶的介电谱曲线，无法获得全频段上重合的标准曲线，只有在弥散响应主导的频段上可获得重合曲线[14]。

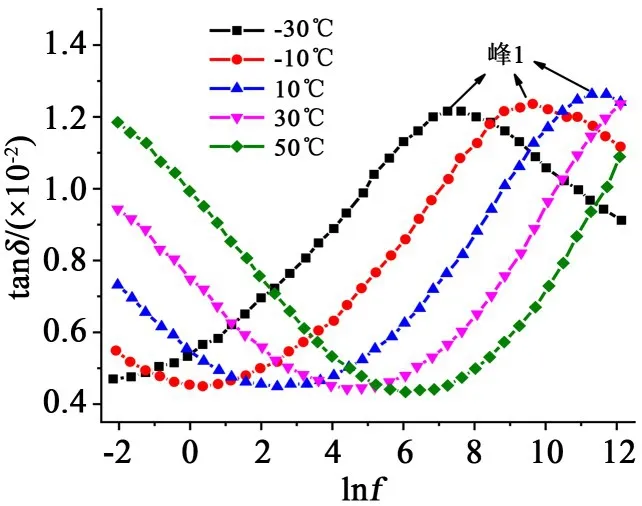
图3 不同温度下环氧试样的介质损耗频谱Fig.3 Dielectric loss spectra of epoxy samples at different temperatures

由上述分析可知，多个弛豫过程叠加的介电谱曲线，在随着温度升高向右平移的同时，也可能由于温度对不同弛豫过程的影响程度不同，使叠加后的介电谱曲线产生“温漂”现象。本研究采用的环氧树脂复合绝缘试样含有Al2O3粉末填料，材料内部晶相与非晶相之间会产生许多界面，因此包含多种弛豫过程。文献[13]的研究也指出，30℃时环氧树脂转向极化的特征频率为e13Hz，本研究的测量频段为10-3～103Hz，即e-6.91～e6.91Hz，故可认为本文所测频段主要包含转向极化弛豫过程和界面极化弛豫过程。

在应用频-温平移法分析曲线时，发现不同温度的介电谱曲线无法平移重合，这正是多种弛豫过程的介电谱曲线叠加的结果。ε′表征材料的电荷积累，单一弛豫过程伴随的电荷积累随着频率降低单调增加。从图1(a)可看出，30℃时ε′曲线在f≤e-2Hz时的曲线斜率明显上升，其原因是参与界面极化的运动单元在此频段逐渐跟得上频率的变化，因此电场频率继续降低，由于界面极化积累的电荷量将明显增加；而转向极化的特征频率远高于此频段，参与转向极化的运动单元已经完全跟得上电场频率的变化，即使电场频率进一步降低，由于转向极化积累的电荷量也不会明显增加。同时温度升高两种极化的弛豫时间均减小，ε′曲线均向右平移，界面极化在ε′的组成部分ε′01的变化率较大，主要影响ε′曲线的变化趋势和形状，而转向极化在ε′的组成部分ε′02的变化率较小，温度升高时对ε′曲线主要起整体向上抬升作用，两者综合作用使ε′曲线随着温度升高曲线形状无明显改变，但整体向右上漂移。

ε″表征介质中的能量损耗，单一弛豫过程的能量损耗随频率降低呈现先增大后减小的趋势，在弛豫的特征频率处达到最大值。在图1(b)所示频段，界面极化损耗随频率降低而升高，转向极化损耗随着频率降低而降低。随着温度上升，极化损耗曲线均向右平移，但由于两种极化的运动单元和运动形式不同，受温度的影响程度亦不同，温度对活化能大的弛豫过程影响更大。在相同的温升下若界面极化所受影响较大，则两种极化叠加后就会导致ε″曲线随温度升高呈现向右上方漂移的趋势。

由上述分析可知，“温漂”现象的原因为多个满足时温等效原理的弛豫过程叠加引起的曲线漂移。“温漂”会导致应用频-温平移法时无法获得重合主曲线，进而影响活化能的求取，因此需要探究“温漂”现象的机制和规律，改进频-温平移法。

2 求取活化能的改进介电谱法

2.1 弛豫过程对介电谱特征参数的影响规律

为消除“温漂”现象对频-温平移法求解的影响，需要对此现象进行进一步分析。本研究出现的“温漂”现象是转向极化和界面极化过程的叠加结果，所以首先分析这两种极化过程对ε′、ε″曲线的影响机制和规律。为清晰说明两种弛豫过程对介电谱曲线的影响，用表达多弛豫过程的改进德拜方程分解表示ε′、ε″[21-23]，根据上文分析，在选用的测量频段内主要存在界面极化和转向极化两种极化过程，故选用二阶方程进行等价分析，如式（3）所示。

式（3）～（4）中：α1、α2表示界面极化、转向极化的弛豫时间的分散程度；τ01、τ02为界面极化、转向极化的弛豫时间；k0ωα0表示电导损耗；ε∞为高频介电常数；ε′01、ε′02分别对应式（3）的第二、三项，代表界面极化、转向极化在ε′的组成部分；ε″01、ε″02分别对应式（4）的第二、三项，代表界面极化、转向极化在ε″的组成部分。

寻找最优解使拟合数据（ε″model）和实测数据（ε″measure）的误差平方θ最小，如式（5）所示。

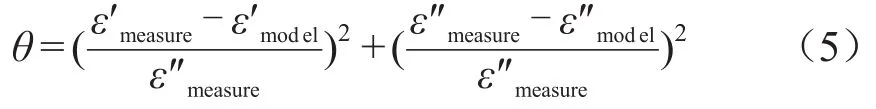
拟合图1中的实测数据，结果如图4和表1所示。误差平方θ值越小表示拟合效果越好。

分离得到两种极化随温度、频率的变化如图5所示。从图5可以看出，温度升高导致界面极化、转向极化弛豫时间均缩短，ε′01、ε′02均向右平移，但在f≤e-2Hz频段，ε′01的变化率明显大于ε′02的变化率，符合前文分析的此频段内转向极化已进行较为完全、界面极化蓬勃发展的物理机制。温度升高，ε′01、ε′02曲线叠加导致ε′曲线形状基本不变、向右上方移动的变化趋势，呈现“温漂”现象。

图4 不同温度下ε′、ε″曲线的改进德拜模型拟合结果Fig.4 Improved Debye model fitting results of ε′and ε″at different temperatures

表1 环氧树脂试样介电谱的改进德拜模型参数Tab.1 Improved Debye model parameters for dielectric spectra of epoxy resin samples

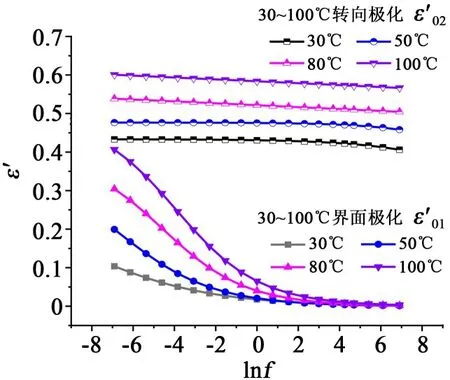
图5 不同温度环氧树脂ε′随频率的变化Fig.5 The ε′of epoxy resin varies with frequency at different temperatures

不同温度时ε′曲线极小值点相对于30℃时极小值点的变化量以及极小值点处ε″01、ε″02相对于30℃时的变化量如图6所示（电导损耗可忽略不计）。从图6可以看出，曲线极小值点处的ε″01相对于30℃时的变化量随着温度升高而增大，ε″02相对于30℃时的变化量随温度升高而减小，但随着温度升高界面极化增大的损耗大于转向极化减小的损耗，综合导致极小值点升高，曲线出现“温漂”现象，这一拟合结果符合上文分析的温度对两种弛豫过程叠加影响的物理机制。

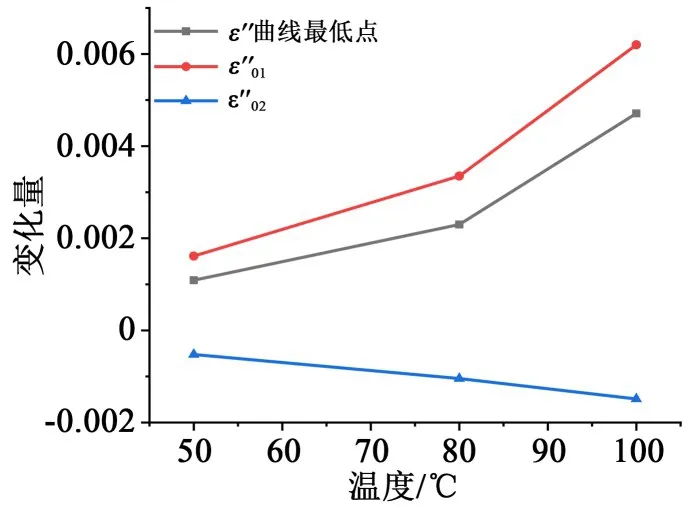
图6 环氧树脂不同温度下ε″曲线最低点及极小值点ε″01、ε″02相对于30 ℃时的变化量Fig.6 The change of the minimum of the ε″ curve and the minimum value of ε″01and ε″02at different temperature relative to that at 30℃

由ε″的拟合结果发现，在图1(b)所示频段两种极化过程叠加影响且影响程度相近，出现“温漂”现象导致无法使用频-温平移法。拟合结果还发现低于图1(b)所示频段，电导损耗随频率降低急剧上升，ε″不再反映弛豫过程与频率的关系，亦不再适用频-温平移法。由ε′的拟合结果发现，在f≤e-2Hz频段ε′01的变化率明显大于ε′02的变化率，且ε′不受电导的影响，基于此，本文对ε′曲线f≤e-2Hz频段进行进一步分析，探究使ε′曲线反映单一弛豫过程的处理方法。

材料内某种弛豫形式对应的运动单元类型和尺寸具有分散性，导致弛豫的分布频率具有一定分散性，因此不同弛豫形式存在的频段有所交叠。频率介电谱描述复介电常数随电场频率变化而变化的现象，虽然特征频段有所交叠，但主要弛豫过程决定着介电谱曲线的变化趋势[24]。以环氧树脂试样在100℃的ε′曲线为例，界面极化和转向极化对ε′曲线变化趋势的影响程度如图7所示。从图7可以看出，ε′相对上一个较高频点的变化量中，界面极化占主要作用，转向极化占次要作用。同时ε′曲线在f≤e-2Hz时变化率急剧上升，根据低频弥散理论[17]可确定此为界面极化的特征频段，故在此频段内界面极化为主要弛豫过程，转向极化为次要弛豫过程。

图7 ε′变化量与极化变化量占总变化量的比例Fig.7 Ratio of ε′and polarization change in total change

图8 环氧树脂ε0i′随频率的变化情况Fig.8 Change of ε0i′with frequency for epoxy resin

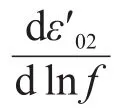
2.2 改进的介电谱法与计算流程

基于上文分析所得主要、次要弛豫过程对介电谱曲线的影响规律，提出一种求取活化能的改进介电谱法，介电谱响应曲线满足式（6）所示关系。

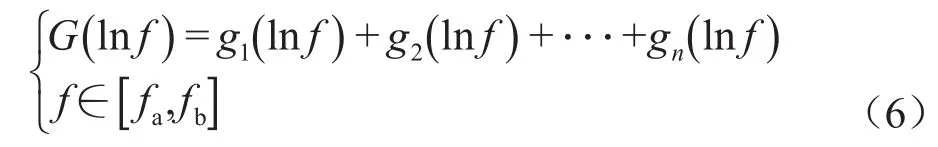
式（6）中：G(lnf)为总介电谱曲线（tanδ、ε′、ε′曲线）；g1(lnf)为各个弛豫的介电谱曲线；n为总介电谱曲线包含的弛豫个数；[fa，fb]为某种弛豫特征频率所在的特征频段。

假定[fa，fb]为弛豫1的特征频段，则认为g1(lnf)为关于f的高阶项，其余gi(lnf)为常数项可得到式（7）。

通过式（7），使介电谱曲线的形状曲线作为平移参量，总介电谱曲线G(lnf)关于lnf的一阶导数G′(lnf)可以消除随频率f变化不大的次要弛豫过程对介电谱曲线的影响，近似表征单一弛豫过程，叠合不同温度下的G′(lnf)曲线即可求得主要弛豫过程的活化能，避免“温漂”现象造成的求解误差。

本方法亦可推广到求取特征频段较高的弛豫峰型介电响应活化能，选用 tanδ或ε′作为 G(lnf)。弛豫峰型介电响应过程在介电谱曲线出现弛豫峰，在此弛豫峰处始终满足G′(lnf)=0，获得不同温度G′(lnf)=0对应的频率即可求取转向极化的松弛活化能，表征偶极子克服分子间作用力沿电场方向排列需要克服的势垒。

由以上分析可知，使用改进介电谱法求解活化能的流程如下：首先需根据ε′曲线上是否出现弛豫峰以及弛豫峰所处频率，确定求取该弛豫类型活化能所要平移的参量。偶极子主导的转向极化在tanδ或ε′曲线出现弛豫峰，选择ε′曲线作为平移参量；对于界面极化等特征频段较低的低频弥散弛豫过程，选择ε′曲线作为平移参量。其次需要确定弛豫的特征频段，为避免“温漂”现象对求取活化能的影响，用介电曲线的一阶导数曲线G′(lnf)近似表征单一弛豫过程，曲线沿频率轴的平移量只反映温度对弛豫时间的影响，叠合不同温度下的G′(lnf)曲线即可求得主要弛豫过程的活化能。

3 改进法的有效性分析与验证

为验证改进方法的有效性，分别以改进介电谱法、德拜拟合数据法、原频-温平移法分析环氧树脂试样的ε′曲线。其中，用改进介电谱法求取界面极化活化能时，选用ε′的一阶导数G′(lnf)作为平移量，沿频率轴平移G′(lnf)曲线获得重合主曲线。而原频-温平移法无法获得重合主曲线，且“温漂”现象导致曲线平移量增大，势必导致求得的活化能数值偏大。3种计算方法求得的界面极化活化能如表2所示。

表2 3种计算方法求得的界面极化活化能Tab.2 Interfacial polarization activation energy obtained by three calculation methods

从表 2可以看出，Ea1、Ea2相差不大，Ea3远大于Ea1、Ea2，可认为改进介电谱法可以提高计算精度，使所求活化能有明确物理意义，即表征低频弥散过程中载流子越过势垒沿电场做定向移动在界面处聚集需要的能量。

改进介电谱法对于含多种弛豫过程的复合电介质也具有适用性，在多种弛豫过程叠加的频段中，可消除次要弛豫过程对求解活化能的影响。但须注意的是，在应用改进的介电谱法计算活化能而对介电谱曲线求导时，可能会放大由于测量精度造成的介电谱曲线的局部偏差。因此，一方面需要提高测量的精度，保证后续分析的基础；另一方面，可以采用Savizky-Golay滤波等方式使求导曲线变得平滑。

大量试验数据表明，绝缘材料的性能劣化，主要反映在低频介电性能的改变[25]。老化会由小到大、由部分到整体地改变材料的微观结构，影响微观运动单元的弛豫过程。活化能表征材料内部微观运动单元在电场作用下发生有限制运动需克服的势垒，可以从微观层面反映老化对微观运动单元的作用。而活化能计算的精确与否决定了用活化能表征老化状态的可行性，改进后的求解方法避免了“温漂”现象对平移求解的影响，增加了活化能计算的精确性，从而能更明显地反映老化过程中活化能的变化趋势。

4 结论

（1）基于介电谱所测物理量对应的物理内涵，明确了频-温平移法的理论基础为温度对弛豫时间的影响关系。针对目前频-温平移法所求活化能的物理内涵不清的问题，划分了不同弛豫种类适用的平移参量，弛豫峰型介电响应适用的物理量为tanδ或ε′，低频弥散型介电响应适用的物理量为ε′。通过改进德拜方程，分离ε′和ε′的组成部分，得到各组成部分随频率的变化状况。求解弛豫过程的活化能时，需针对不同弛豫过程选择不同的平移物理量。

（2）环氧树脂试样的介电谱曲线均出现“温漂”现象，原因是ε′和ε′这两种曲线为多种弛豫过程介电响应过程的叠加，温度对不同弛豫过程的影响程度不同，叠加导致总的介电谱曲线随着温度升高向右上漂移。“温漂”现象对频-温平移法的干扰较大，需要进一步改进基于介电谱的活化能求取方法。

（3）提出了求取活化能的改进介电谱法。根据在某弛豫的特征频段，主要弛豫过程主要影响介电谱曲线的变化趋势和形状，借助一阶导函数只包含原函数形状信息的特点，用总介电谱曲线G(lnf)关于lnf的一阶导数G′(lnf)消除随频率f变化不大的次要弛豫过程对介电谱曲线的影响，近似表征单一弛豫过程。并用环氧树脂为例验证，求解出环氧树脂界面极化的松弛活化能为78.538 kJ/mol，与德拜拟合数据法所得的活化能相差不大，验证了该改进介电谱法的有效性。