基于MOGA的串联机械臂参数优化设计
王宪伦,段奕林
(青岛科技大学机电工程学院,山东 青岛 266061)
工业机械臂通常由关节和杆件组成,一般分为3种,分别是串联机械臂、并联机械臂以及混联机械臂[1]。由于串联机构具有工作空间大、末端执行器运动较灵活以及易于控制等特点,因此应用较为广泛[2]。为了提高机械臂的使用寿命,降低机械臂的最大应变以及最大应力,Calvin、赵铁军、时凯飞、郭炬[3-6]等分别对机械臂进行了结构设计及静力学分析研究。本文所设计的机械臂主要供教学使用,要求该机械臂具有良好的灵活性以及可操作性,故采用六自由度串联结构。
1 机械臂主要部件优化设计
对本文设计的六轴串联机械臂关键部件进行优化设计,目的是在满足强度要求的前提下改进原有设计中不合理的尺寸,降低机械臂在工作过程中的形变量。首先对该机械臂进行了简化,简化后的结构示意图如图1所示,然后对图1中的R03部件进行分析优化,优化其相关尺寸。

图1 简化后主要部件示意图
优化设计的思路是在满足原设计要求的前提下,求解所给定的目标函数的极值。优化设计步骤如下[7]。
1)选择设计变量。设计变量是指根据优化目标对多个参数进行选择,最终确定需要优化的参数,设计变量用X=[x1,x2,…,xn]T表示。
2)确定约束条件。在实际设计过程中,设计变量值并不是随意选取的,会根据实际情况确定一个取值范围进行限制,而这种限制就是约束条件,但这种限制并不一定只有一个,约束条件的区域集合可以表示为S={x|gi(x)≤0,i=1,2,3,…,n},其中gi(x)为状态变量。
3)确立目标函数。为了对当前优化设计进行评价,需要构造一个涵盖全部设计变量的评价函数,即目标函数,它随着设计变量的变化而变化,用F(X)表示。一般可以将优化问题分为两类,即单目标优化和多目标优化。事实上,目标越多,优化设计后的整体性能可能会越好,但求解的难度也相应会增加。
4)建立数学模型。优化设计的数学模型的表达式为:

(1)
2 R03部件参数优化
使用三维建模软件对机械臂进行设计,预期末端负载为1 kg。首先将建立好的三维模型导入Workbench中,模型材料设置为结构钢,然后划分网格,得到高质量的六面体网格。考虑到其他部件的质量以及电机自重的影响,将模型的一端固定,然后添加100 N的远程力,即负载为10 kg,比预期多9 kg。求解得到在初始设计尺寸下该模型加载10 kg负载时的应力及变形云图,如图2、图3所示。

图2 应力云图

图3 变形云图
对该模型进行基于响应面的优化设计,并对输入参数添加约束条件。3个设计变量P1,P2,P3的取值范围见表1。

表1 定义变量参数 mm
对该优化方案添加设计样本点,设计样本点的优劣直接影响基于采样点结果的响应面的精度,共有7种生成设计样本点的方法:1)中心组合设计(central composite design,CCD) 法;2)空间填充设计(optimal space-filling design) 法;3)box-behnken设计(box-behnken design,BBD) 法;4)用户自定义(custom) 法;5)自定义与抽样(custom+sampling) 法;6)稀疏网格初始化(sparse grid initialization) 法;7)拉丁超立方体抽样设计(latin hypercube sampling design) 法。
本文使用Box-Behnken 设计法自动生成样本点,由于此种设计法不包含初始值,故采用用户自定义法将设计初始值添加上去,以便于比较,然后进行求解计算,得到输入与输出之间的参数关系,如图4所示。

图4 求解结果
为了更加直观地表示,所有的设计样本点求解结束之后采用3D形式输出结果,如图5所示。由图5可以看出,P1越小,形变量越大,质量则越小;P2越小,形变量越小,但对质量的影响却不是很大;而对于P3来说,其对形变量的影响不是很大,P3越小,质量会越大,但影响也不是太明显。

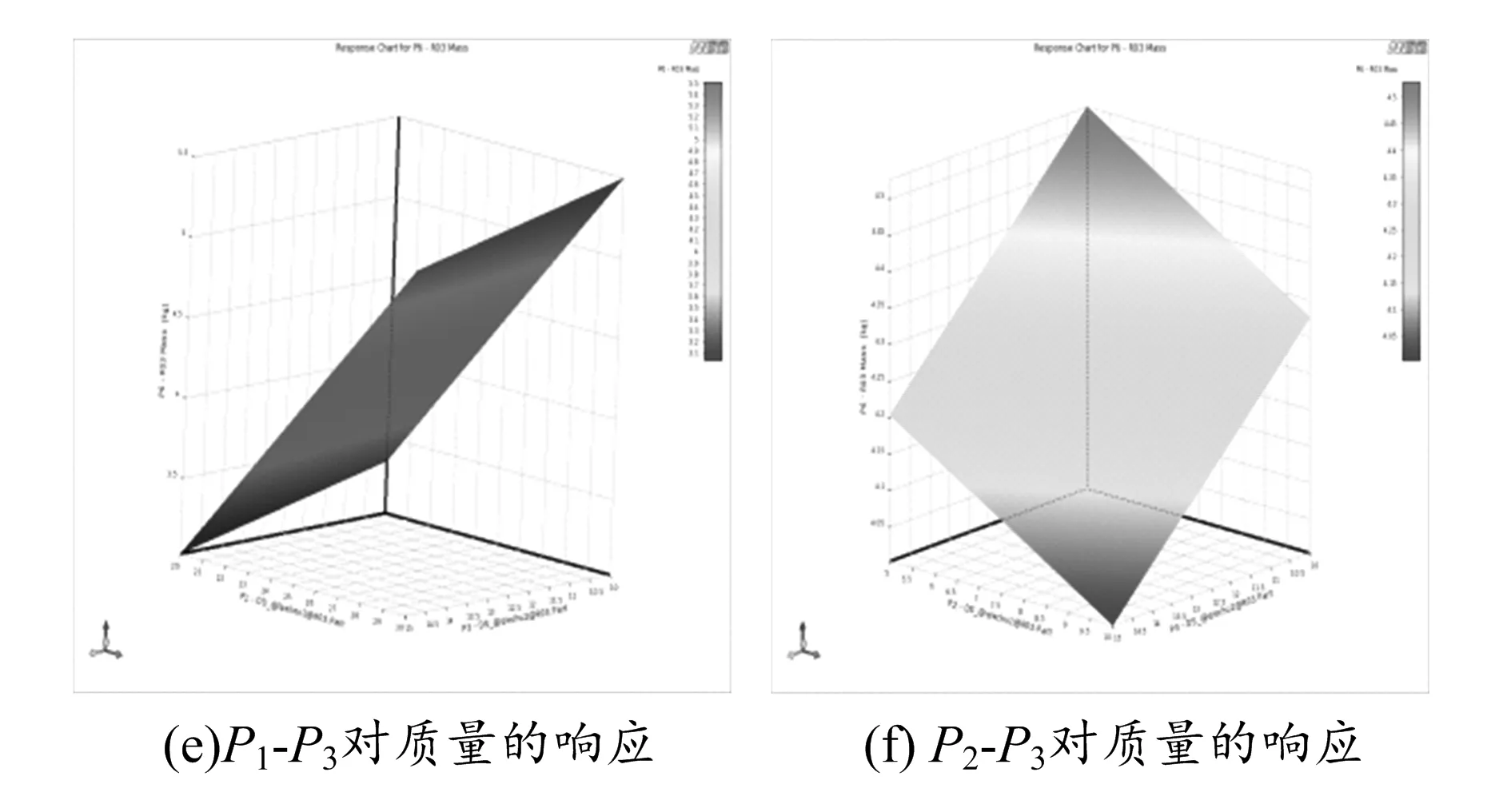
图5 响应曲面
为了能够更加直观地看出输入参数对模型的应力、形变量以及质量的影响程度,给出输出参数的敏感度图,如图6所示。由图可以看出,设计变量P1对模型的应力、形变量以及质量的影响程度远大于另外两个变量,可作为主要设计变量操作,当P1增大时,应力会随之减小,形变量同样减小,只有质量在增大。而设计变量P2,P3对形变量与应力的影响都很小。

图6 输出参数的敏感度
本次优化将优化目标定义为模型的形变量最小,但由于应力和质量这两个参数它们相互制约、相互影响,这就是多目标优化的难点所在,只能在比较结果后得出相对的“最优”。
在定义输出参数的优化目标时,定义输出参数P4即最大应力的求解目标为最小值,但目标重要性定义为最低;定义输出参数P5即形变量的求解目标为最小,将其目标重要性定义为最高;定义参数P6即质量的求解目标为最小,目标重要性定义为默认。
在所有优化目标定义后,使用多目标遗传算法[8](multi-objective genetic algorithm, MOGA)进行参数优化。求解计算,得到如图7所示的3组候选设计点,可以看出第三组候选点是最符合要求的设计点。选取第三组候选点作为最优设计点,再以图6所示的敏感度分析结果作为依据对该组候选点进行圆整修正,得到最佳优化点参数,优化前、后输入参数值对比见表2。

图7 候选设计点

表2 输入参数对比 mm
3 R03部件参数优化结果分析
优化计算结束后,对优化前、后输出参数进行对比,结果见表3。

表3 输出参数对比
从表3可看出,优化后质量增加的同时最大应力在减小,优化后质量虽增加了10.92%,但最大应力和形变量分别下降了22.00%和12.50%。此次优化把模型的形变量放在了首位,可见此次优化效果显著,对于提高机械臂整体的安全性与可靠性有很大帮助。若需要进一步优化模型质量,可以添加加强筋对模型进行强化,这样可以通过进一步减小输入参数P1的值来减小模型质量。
4 结束语
本文运用Workbench对六轴串联机械臂的主要部件进行了静力学分析,对其质量和部分尺寸参数进行了多目标参数优化,研究了尺寸优化对机械臂性能的影响。采用多目标遗传算法进行求解计算,得到了一组可以达到预期目标的最优设计点。本文的研究成果对一般机械臂的设计与优化有一定的参考价值,在缩短机械臂设计周期的同时,能够保证机械臂的可靠性。

