高温高压模拟井筒流固耦合传热建模与数值求解
侯永强, 贾光政, 李鸿霏, 苗夏楠, 赵崇任
(东北石油大学机械科学与工程学院, 大庆 163318)
随着油气田勘探和开发井深的增加,井下的油层温度和压力也相应增加,对射孔器材耐温耐压性能也提出了更高的要求[1]。研制的高压模拟井筒加温系统用于模拟井下高温环境,对射孔器材进行耐高温高压性能检测,为射孔器材性能研究和设计提供井下模拟试验条件[2]。由于模拟井筒内为超高压流体,无法直接测量密封的模拟井筒中心位置的流体温度,因此,研究并求解其升温过程中温度场的分布对射孔器材耐高温高压性能检测具有重要意义。中外学者对腔体传热问题的研究大多简化为给定内部边界条件的封闭腔体内自然对流换热过程,且针对方形腔体结构进行建模与研究[3],针对圆柱形厚壁井筒的厚壁与腔体内流体的耦合换热过程研究较少[4-5],对模拟井筒流固耦合传热过程的数学模型与数值求解方法的研究更鲜有报道[6]。同时,自然对流换热数学模型为非线性耦合问题,求解该数学模型的计算量巨大,因此高效数值求解自然对流换热问题也是研究的重点[7-10]。针对上述问题进行模拟井筒热流固耦合换热研究,求解出模拟井筒的流固耦合传热径向温度分布规律,对模拟井筒加温系统的设计与温度控制有重要的工程意义。研究圆柱形厚壁井筒的厚壁与腔体内流体的热流固耦合换热数值求解方法也具有重要的理论和科学意义。
1 模拟井筒耦合传热物理模型
超高压模拟井筒加温系统主要由井式加热炉、模拟井筒、风循环系统和支撑底座等组成,结构示意如图1所示。模拟井筒为内部能够承受射孔弹引爆产生的压力冲击的高强度空腔厚壁金属圆柱体。
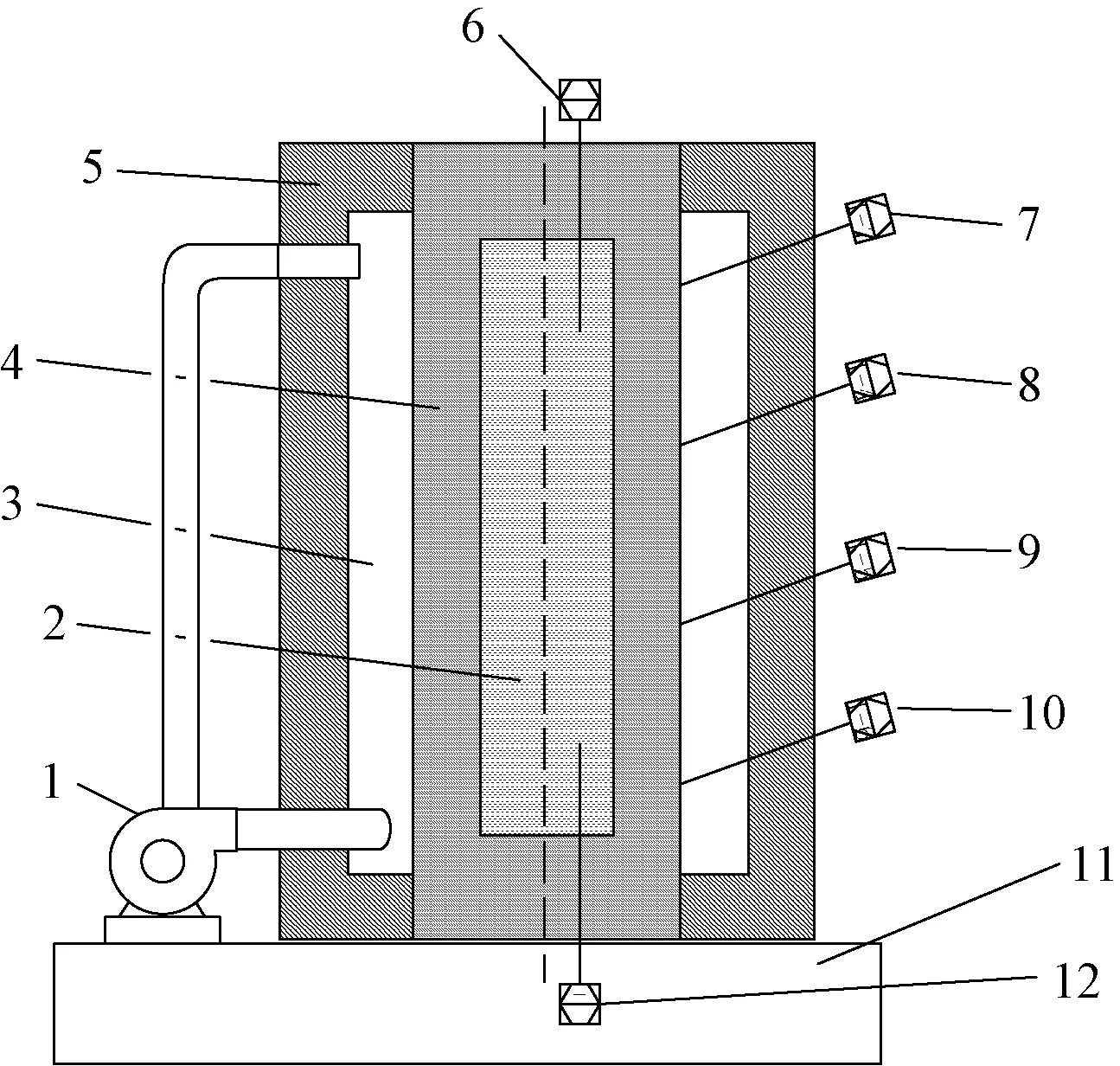
1为风循环系统;2为工作介质;3为空气夹层;4为模拟井筒; 5为井式加热炉;6、7、8、9、10为温度传感器;11为支撑底座; 12为温度传感器图1 加温装置结构示意图Fig.1 Schematic diagram of the heating device
井式加热炉与模拟井筒之间的传热通过风循环系统的强制对流对模拟井筒外表面进行加热;模拟井筒外表面受热后热量沿厚壁进行热传导到达内壁,在内壁处进行流固耦合传热;模拟井筒内充满水,模拟井筒选用低膨胀系数的PCrNi3MoVA Ⅳ钢材制作,壁厚0.18 m,可承受230 MPa的压力,加热过程中认为模拟井筒体积增加量可以忽略不计。模拟井筒内部水被加热到200 ℃,加热过程中产生100 MPa的压力,为高温高压饱和水[11]。热量驱动模拟井筒内的流体(饱和水)形成自然对流,使内部流体温度逐渐升高。通过温度闭环实时监测,调节炉膛内部的电热元件加热功率,控制模拟井筒外表面加热温度均匀。根据以上分析,加热过程的物理模型包括圆柱型形壁容器的外壁被均匀加热、圆柱形厚壁容器与腔体内部流体的热流固耦合换热、内部流体由于温度不均匀而形成密度差在重力场中产生浮升力引起对流换热。
模拟井筒为圆柱体,加热温度场径向对称,模拟井筒的导热模型可以用二维模型来描述。由于井筒上下端采取保温措施,可不考虑模拟井筒两端散热,柱坐标系下模拟井筒的二维物理模型如图2所示。图2中,r坐标轴为水平方向,r1、r2分别为井筒的外表面半径与内表面半径,m;z坐标轴为垂直方向,为物理模型的对称轴;H为圆柱形封闭腔体的长度,m;水平壁面为绝热面,竖直外壁面为高温面,竖直内壁面为流固耦合传热壁面。
2 模拟井筒耦合传热数学模型
2.1 模拟井筒传热控制方程
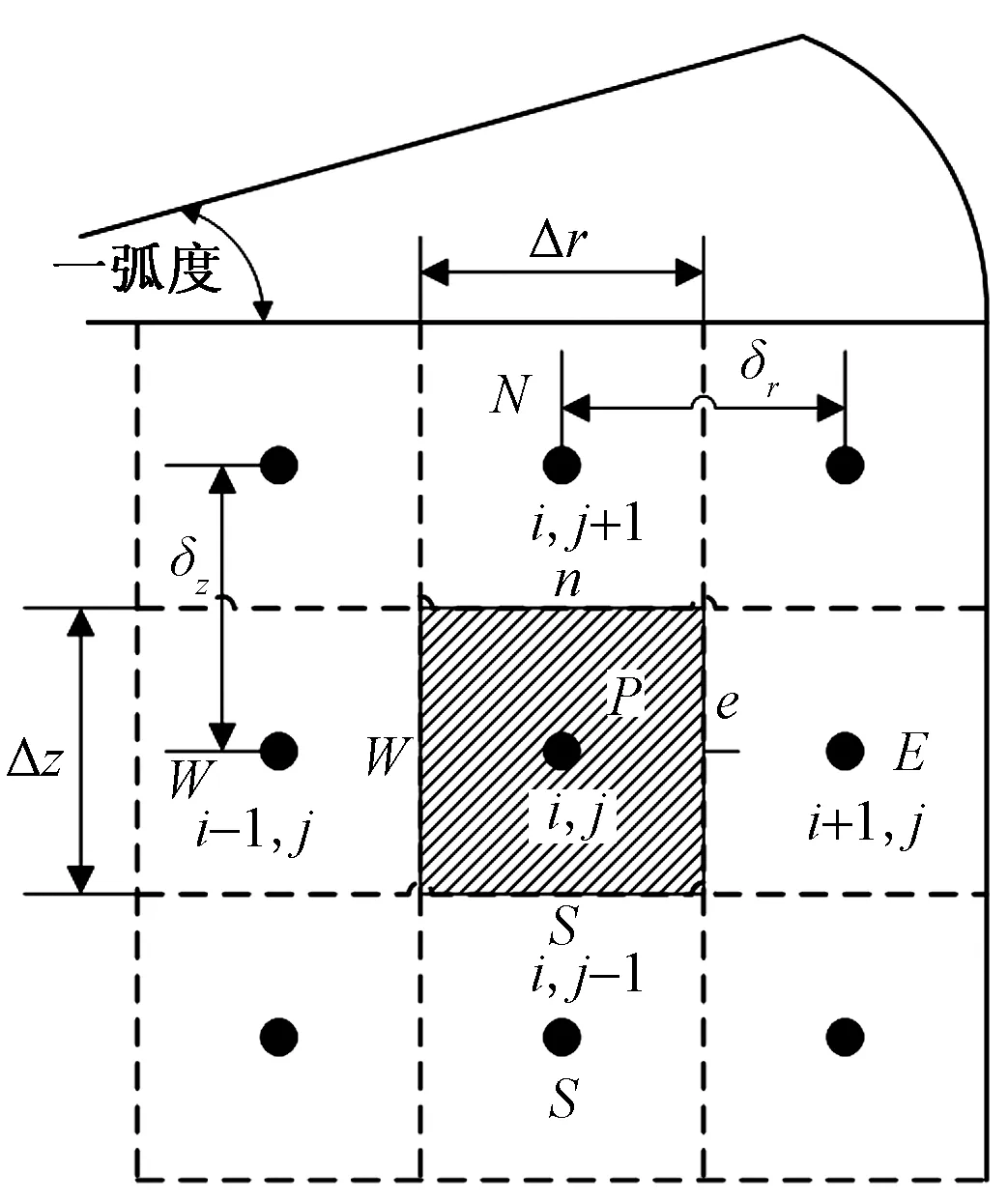
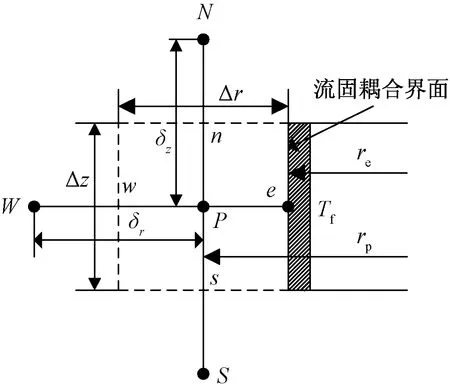
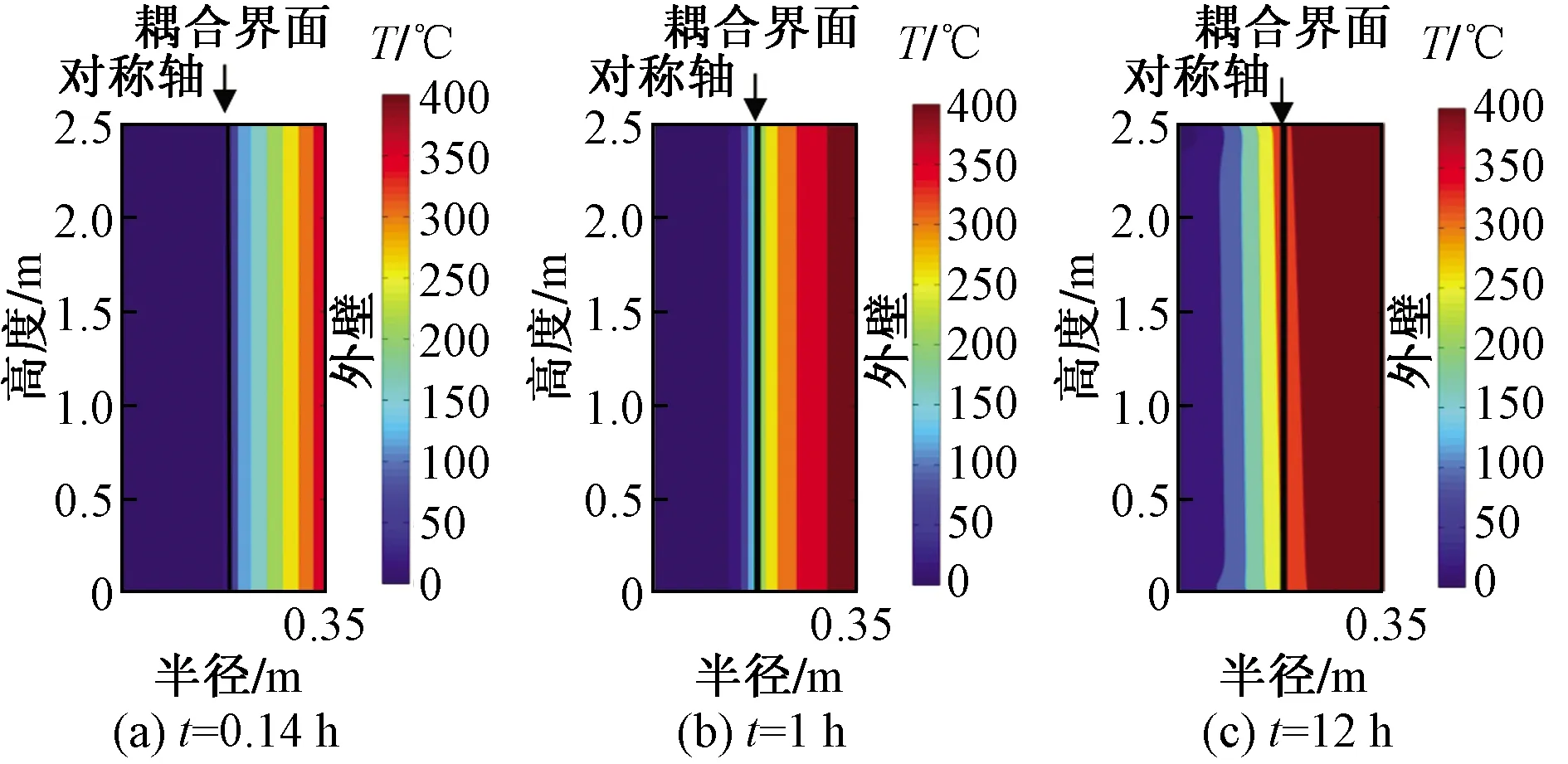
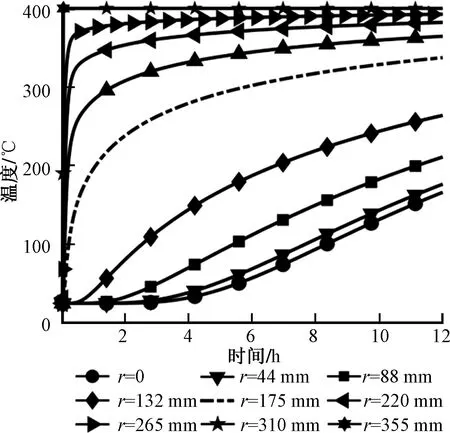
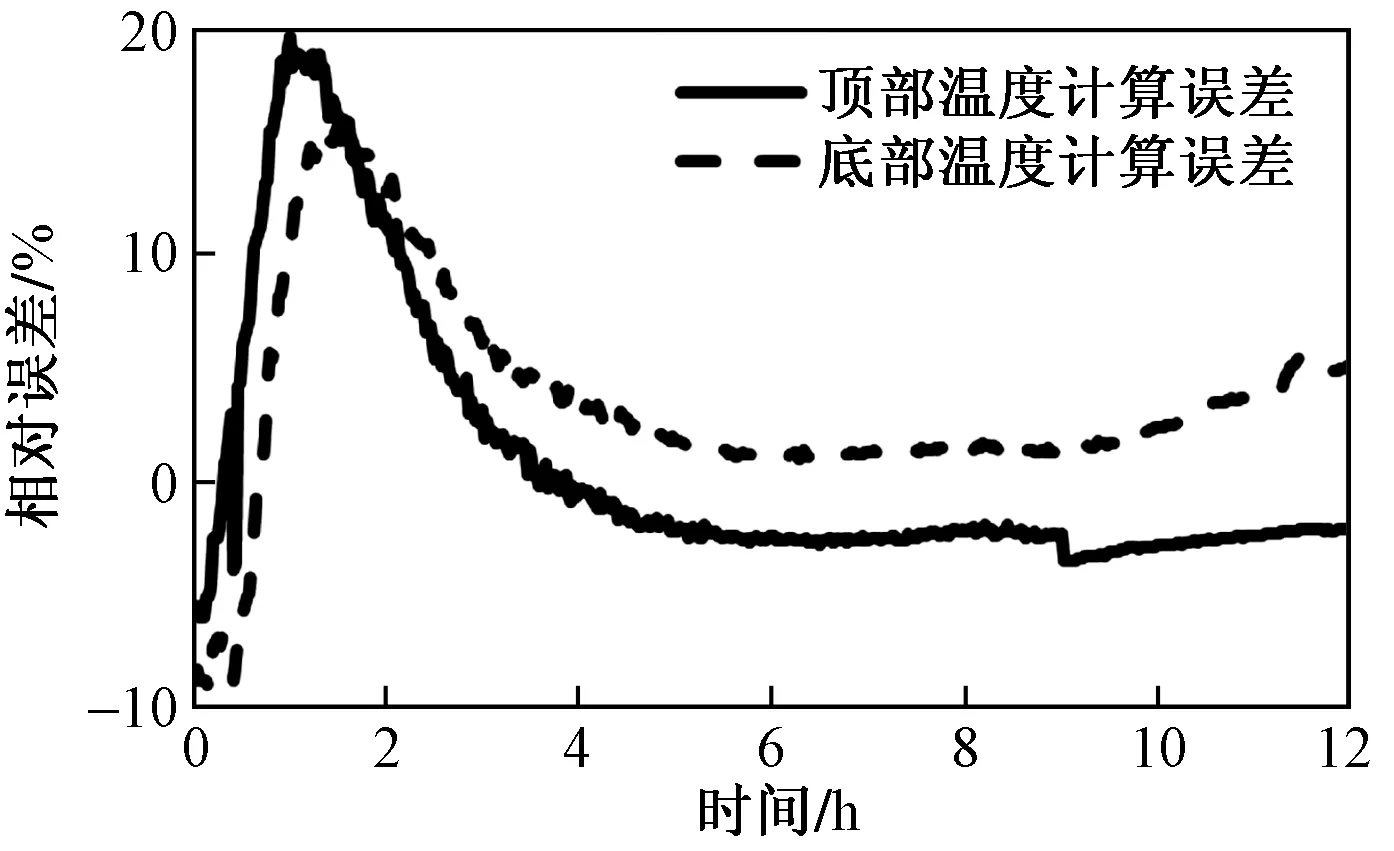
在柱坐标系下,建立二维非稳态模拟井筒传热控制方程。根据能量守恒定律和傅里叶定律建立模拟井筒(r2 (1) 式(1)中:TS为模拟井筒的温度分布,K;λ1为模拟井筒的导热系数,W/(m·K);ρ1为模拟井筒的密度,kg/m3;c1为模拟井筒的比定压热容,J/(kg·K);r为模拟井筒的半径,m;z为模拟井筒的高度,m;t为时间变量,s。 模拟井筒从初始温度(室温25 ℃)开始加热,其内部流体(饱和水)的密度与温度的函数关系在线性区域,采用Boussinesq假设,密度仅考虑动量方程中与浮升力有关的项,其余各项中的密度为常数。模拟井筒内部流体为高温高压饱和水,其自然对流换热(r (2) ρogβ(Tf-To) (3) (4) (5) 式中:u、v分别对应z、r方向的速度,m/s;t为时间,s;Tf为模拟井筒内流体温度,K;To为初始温度,K;μ为模拟井筒内流体动力黏度,Pa·s;p为模拟井筒内流体压力,Pa;ρo为初始温度时模拟井筒内流体密度,kg/m3;β为模拟井筒内流体体积膨胀系数,K-1;a2为模拟井筒内流体热扩散率,m2/s;g为重力加速度,m2/s。 模拟井筒内壁与其内部流体在耦合边界上的温度连续方程、热流密度连续方程为[12] Tfp=Tsp (6) qf=qs (7) 式中:Tfp和Tsp分别为耦合界面上流体与固体的温度;qf和qs分别为耦合界面上流体边界处与固体边界处的热流密度。 建立的模拟井筒耦合传热数学模型需要采用数值解法求解。模拟井筒厚壁与其内部流体的流固耦合传热采用分区计算和边界耦合方法求解。 3.1.1 模拟井筒厚壁区域控制方程的离散 图3 圆柱轴对称坐标的网格系统Fig.3 Grid system with cylindrical axisymmetric coordinates 模拟井筒厚壁控制方程应用有限差分法求解,采用内节点法进行网格划分。取一个弧度的中心角所包含的范围作为研究对象,圆柱轴对称坐标的网格系统如图3所示。节点P所代表的控制容积由界面N-W-S-E围成;P、N、S、W、E表示所研究的节点及相邻的4个节点;i和j分别对应r和z方向的节点位置;r、z为空间坐标,将模拟井筒厚壁计算区域半径(r)划分为M等份,高度z方向划分为N等份,得到M×N个节点;半径(r)、高度(z)、时间(t)的离散变量分别用r、z、t表示;n表示非稳态的时间层,n+1表示时间间隔为t的下一时间层。δr、δz表示相邻两节点间的距离。r、z表示相邻两界面间的距离。采用时间项向前差分和空间项中心差分的显示差分格式,将式(1)进行离散化得 (8) 3.1.2 内部流体区域控制方程的离散 模拟井筒内部流体区域采用交错网格进行离散,流体区域半径r划分为B等份,高度z方向划分为C等份,得到B×C个节点。空间与时间坐标变量的表示方法与模拟井筒厚壁计算区域相同。应用有限差分方法离散控制方程[式(2)~式(5)], 其中对流项用二阶精度的Adamas-Bashforth 格式显式处理,黏性项用Crank-Nicholson 格式离散,空间离散采用二阶中心差分格式。应用以上离散格式,将模拟井筒传热控制方程进行离散化得 (9) (10) (11) (12) 差分算子的定义为[13] Dr()()i-1/2,j]/Δr (13) Dx()()i+1/2,j-()i-1/2,j]/Δx (14) (15) (16) Lh()i,j=[()()i,j+()i-1,j]/Δr2+[() (17) Lm()i,j=[()()i-1,j]/2Δr (18) 3.2.1 模拟井筒控制方程数值求解 令r=ir,z=jz,F0=1t/ρ1c1rz,模拟井筒厚壁区域的控制方程如式(8)所示,整理得 (19) 3.2.2 模拟井筒内部流体区域的控制方程数值求解 流体区域采用投影法求解,模拟井筒内部流体区域的控制方程为不可压缩流动的Navier-Stokes方程组,是一个非线性很强的方程组,直接耦合数值求解该方程组计算量巨大[14],常用的计算方法都是将速度和压力解耦求解[15]。投影法最初由Chorin提出,其原理主要是Helmholtz-Hedge矢量分解定理[16],任意矢量场可以分解为一个无散度矢量场和一个无旋矢量场之和。投影法把一个非线性系统化成一系列椭圆问题,解耦的同时也解决了非线性项的问题,解耦后的Navier-Stokes方程分成三步进行求解,求得速度和压力值,免去了在各步之间反复迭代过程。因而能非常高效的求解模拟井筒内部流体区域的控制方程。 采用Helmholtz-Hedge矢量分解方法,通过引入中间速度u*、v*,把式(10)分解为式(20)、式(21): (20) (21) 把式(11)分解为式(22)、式(23): (22) (23) 求解分解后的动量方程[式(20)、式(22)],求解中间速度场u*、v*。 离散的压力Poisson方程为 ap′i,j+bp′i+1,j+cp′i-1,j+dp′i,j+1+ep′i,j-1+f=0 (24) (25) 式(25)中:m为迭代次数;ω为松弛因子,ω>1时为超松弛迭代。 由求得的u*、v*、pn+1,应用式(21)、式(23),求得n+1时刻的un+1、vn+1,应用式(12),求得下一时刻的温度T。 在计算过程中为了节省计算资源,提高计算速度,井筒厚壁控制区域与井筒内流体区域分别满足各自计算区域稳定性的网格数。耦合界面处固体与液体的网格数不同的情况下,热流密度采用线性插值方法进行数据的传递,保证空间上的数据传递正确。 热流固耦合热流密度连续方程采用热平衡法求解。热平衡法直接将能量守恒原理以及傅里叶导热定律应用于节点所代表的控制容积。热流固耦合边界坐标网格系统如图4所示。 图4 热流固耦合边界坐标网格系统Fig.4 Fluid-solid coupled heat transfer boundary coordinate grid system 图4中对于节点P,在t时刻所代表的控制容积(由虚线N-W-S面围成)建立热平衡关系,各项热流量都以进入单位体积元体P的方向为正。N、S、W节点分别对应节点P相邻的上部、下部和左边节点。根据能量守恒定律,非稳态节点的能量守恒表达形式为 (26) 从节点N,通过界面n传导到节点P的热流量可表示为 (27) 从节点S,通过界面s传导到节点P的热流量可表示为 (28) 从节点W,通过界面s传导到节点P的热流量可表示为 (29) 根据式(7)耦合边界上热流密度连续,节点P与内部流体换热的热流量可表示为 (30) (31) 内边界单位体积元体P′的能量守恒方程为 φN+φS+φW+φP=ΔEP′ (32) 将式(27)~式(31)代入式(32),整理得 a′PT′P=aPTP+aNTN+aSTS+aWTW+afTf (33) 模拟井筒耦合传热数学模型的边界条件为:上、下表面z=0、z=H处绝热,r=r1壁面为高温面,r=0为对称轴,r=r2壁面为流固耦合传热面,边界位置如图2所示。压力修正方程的边界条件为Neumann边界条件,即p/n=0(n为外法线)[17]。其他边界条件如表1所示。 表1 模拟井筒耦合传热边界条件Table 1 Simulated wellbore coupling heat transfer boundary conditions 式(1)~式(7)组成了模拟井筒流固耦合非稳态传热数学模型,采用流体与固体瞬态耦合算法进行求解。即在每个[t,t+t]时间步长内,按照以下步骤进行求解。 (1)假定耦合边界上的温度分布,作为流体区域的边界条件。 (2)对流体区域进行求解,得出耦合边界上的局部热流密度和温度梯度,作为固体区域的边界条件。 (3)按照式(7)求解固体区域,得出耦合边界上新的温度分布,再以此分别作为流体区域的边界条件。重复上述计算步骤直到收敛。 模拟井筒及其内部流体的物理参数为:模拟井筒外壁半径r1=0.355 m;内壁半径r2=0.175 m;高度H=2.5 m。初始温度T0=25 ℃;外壁加热温度400 ℃恒定;模拟井筒铬镍钢的密度ρ1=7 830 kg/m3;比热容C1=463 J/(kg·K)。其他物性参数,如模拟井筒铬镍钢的导热系数(1)、饱和水的导热系数(2)、水的运动黏度ν、水的热扩散率(a)均为对应温度下的物性参数。固体区域半径r方向节点数为M=12;高度z方向节点数为N=157,时间步长dt1=1 s。傅里叶数F=0.051 6即(F<0.25),满足稳定性条件。流体区域经网格无关性验证后取半径r方向节点数为B=32;高度z方向节点数为C=450,时间步长dt2=0.001 s。半径与高度方向CFL数均小于0.1,满足流场计算的稳定条件。 根据建立的模拟井筒耦合传热数学模型和求解方法,按照流固耦合传热求解步骤编写计算程序进行数值求解。加热的初始时间t<0.14 h,此过程中模拟井筒金属厚壁的升温速度远大于其内部水的升温速度。模拟井筒金属厚壁的比热容C1和密度ρ1较大,对模拟井筒外壁恒温加热过程中,金属厚壁需要吸收一定量的热量,模拟井筒内壁与外壁产生较大的温度梯度。模拟井筒内壁面温度升高很慢,基本维持在初始温度25 ℃。模拟井筒内壁面与水之间无温差,没有进行流固热耦合热量交换。t=0.14 h时,模拟井筒内壁面与水之间产生温差,开始进行流固热耦合热量交换。t=0.14 h模拟井筒内水的速度场如图5(a)所示。 由图5、图6可知,加热时间在0.14 h 加热时间在1 h 流体的自然对流由图5(a)变化到图5(b)的状态,水由沿井筒内壁面的快速向上运动,发展到整个流体区域的环状运动。因自然对流比较微弱,模拟井筒高径比较大,在上部和下部形成两个微弱环状自然对流运动。 模拟井筒中心高度位置(高度H=1.1 m)处的径向温度分布计算结果如图8所示,r=0处为模拟井筒径向中心,r=175 mm为流固热耦合处(模拟井筒内壁面),r=355 mm处为模拟井筒外壁面。图8中,0≤r≤175 mm为模拟井筒内部饱和水的温度分布,175 mm 图5 模拟井筒内水的速度场图Fig.5 Simulate the velocity field of water in the wellbore 图6 流固耦合温度场分布Fig.6 Flow-solid coupling temperature field distribution 图7 流体流线图Fig.7 Fluid flow diagram 图8 流固耦合径向温度分布Fig.8 Fluid-solid coupling radial temperature distribution 为了验证计算结果的正确性,采用模拟井筒加温实验装置进行模拟井筒流固耦合传热升温实验。加温实验装置为井式电加热炉,采用晶闸管调节器对电加热功率进行控制调节,实现温度精确控制。图9为模拟井筒加温实验装置结构。通过风循环系统的空气循环对模拟井筒外表面进行均匀加热,主要技术如表2所示。 实验装置炉温调整范围为0~500 ℃,选用WFN型铠装热电偶温度传感器,测量范围为0~1 100 ℃,测试位置为厚壁井筒外壁高度方向均布4个。模拟井筒内温度范围为0~300 ℃,选用WRN型铠装热电偶温度传感器测量范围是0~1 000 ℃,顶部热电偶(图1中的温度传感器6)通过模拟井筒的上端盖插入其内部,测试位置为模拟井筒内液体的高度为H=2.28 m,径向为r=0.1 m处;底部热电偶(图1中的温度传感器12)通过模拟井筒的下端插入其内部,测试位置为高度H=0.22 m,径向位置r=0.1 m处。 仿真计算与实验装置采用相同的物理参数,实测与仿真计算升温曲线如图10所示。仿真计算结果与实验实测数据基本一致,都是初始加热时间段升温速度缓慢,之后温度快速上升,顶部温度略高于底部温度,自然对流效应很弱。图11给出了实测与仿真计算升温曲线的相对误差,初始加热时间段0~2 h相对误差最大,顶部相对误差最大值为18%,低部相对误差最大值为15%。随着加热时间的不断推进相对误差不断减小,顶部和低部相对误差均在5%以内。顶部温度的计算值与实验测试值的均方根误差为4.66 ℃,低部温度的计算值与实验测试值的均方根误差为5.19 ℃。实验测试值与计算值的均方根误差较小。通过实验验证了所建立的数学模型和数值求解方法求解超高压模拟井筒流固耦合传热问题的正确性。 图9 模拟井筒加温实验装置Fig.9 Simulated wellbore heating experiment device 表2 加温实验装置的主要技术参数Table 2 Main technical parameters of the heating experimental device 图10 实测与仿真计算升温曲线Fig.10 Measured and simulated temperature rise curve 图11 仿真计算升温曲线的相对误差Fig.11 Simulation of the relative error of the heating curve 研究了模拟井筒的厚壁腔体与腔体内流体(饱和水)之间的动态耦合传热过程,得出以下结论。 (1)基于模拟井筒耦合传热过程的分析,建立了模拟井筒耦合传热数学模型;应用有限差分法离散模拟井筒耦合传热数学模型,得出井筒厚壁和腔体内流体(饱和水)数学模型的离散格式。 (2)采用投影法对腔体内流体的非稳态自然对流传热数学模型进行数值求解,提高了非线性耦合数学模型的计算效率和求解速度;采用迭代法分别计算井筒厚壁与腔体内流体区域的传热过程,在厚壁与流体的交界处应用热平衡法进行耦合传热计算,实现了对模拟井筒加热过程的求解。 (3)计算结果表明,模拟井筒厚壁升温速度远大于其内部流体升温速度,内部流体具有边界层型流动和传热的特点;模拟井筒整体的升温速度主要受其内部高温高压饱和水的热传导影响,从理论上解释了厚壁模拟井筒加热升温速度缓慢的原因。 (4)实验数据与仿真计算结果的对比分析,验证了所建立的数学模型求解高温高压模拟井筒流固耦合传热过程的正确性。
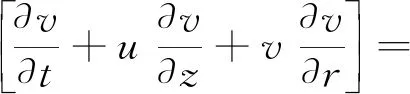
2.2 流固耦合传热的数学模型
3 控制方程的离散及数值求解方法
3.1 控制方程的离散

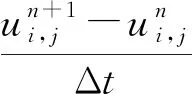
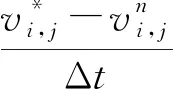
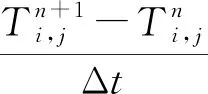

3.2 控制方程的数值求解
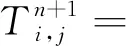
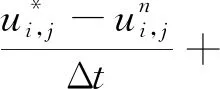

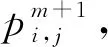
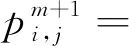
3.3 流固耦合传热的数值求解
3.4 边界条件

3.5 流固耦合传热求解
4 分析及计算


5 实验研究



6 结论

