两级抗滑桩对坡顶建筑物的安全控制研究

刘孟瀚，范秋雁，唐峰

（1.广西大学资源环境与材料学院，广西 南宁 530004；2.中国能源建设集团广西电力设计研究院，广西 南宁 530023）

0 引言

抗滑桩是滑坡防治最主要的措施之一（殷跃平，1998），特别是滑坡体的剩余下滑力较大的情况，应当使用抗滑桩来提高稳定性（张新敏，2004），前人分别利用有限元强度折减法验证了抗滑桩对边坡治理的作用，以及分析边坡变形的位移变形及塑性发展趋势，验证了有限元在抗滑桩及边坡稳定性的研究中的重要意义（董军和苏生瑞，2008；谢荣昌等，2009）。随着土地资源逐渐减少，在边坡的坡脚以及坡顶这样的不利于地基稳定的位置都开始越来越多的出现建筑物，在对边（滑）坡治理中必须考虑已建或规划建设建筑物的稳定和安全，因此多级抗滑桩的边坡支护形式开始被广泛应用。许多学者开展了多级抗滑桩支护作用研究。在基坑支护方面，任望东等（2013）通过建立基坑多级支护有限元模型，计算分析了多级支护的破坏模式及破坏机理，并研究了多级支护结构间的水平距离等因素对基坑稳定性的影响。郑刚等（2017）进行了基坑多级支护大型模型试验，分析了两级支护桩之间距离和二级支护桩桩长对支结构稳定性的影响。在边坡支护方面，黄小艳等（2012）运用FLAC3D 程序模拟分析了双排桩桩后推力与桩前抗力分布形态，为边坡加固提供了参考。赵鑫等（2014）也利用了FLAC3D 程序分析了不同滑坡体土拱效应下桩周及桩间土体位移与应力的变化规律。申永江等（2012）运用土拱理论和极限平衡理论，推导两抗滑桩所承受滑坡推力的计算公式，提出滑坡推力的分配计算方法。唐芬等（2010）建立两级抗滑桩有限元模型，分析不同级距下多级抗滑桩对推力的分担，提出以多级抗滑桩的推力、稳定系数和推力差为目标的优化设计方法。肖世国和何洪（2015）基于弹性地基梁模型，通过迭代算法确定出二级抗滑桩受荷段前侧坡体抗力，给出了相关的理论计算公式。此外，胡洪云（2019）利用数值模拟设计两种抗滑桩布置情况，验证了两级抗滑桩对边坡加固的效果。以上研究主要集中在抗滑桩的内力、桩体位移、边坡的整体稳定性等方面，分析了边坡的破坏机理，并提出了一系列实用的设计和计算方法。但当坡顶建筑物距离边坡坡肩较近时，采用两级抗滑桩的支护形式后，除了考虑边坡的整体稳定性，还必须良好控制坡顶土体位移量，从而保障坡顶建筑物的安全和稳定。孙云普等（2010）通过简化模型，给出了坡顶建筑的安全距离公式，可惜参数较多，很难具体应用实践。专家验证了坡肩的水平位移能反应边坡坡顶土体的变形规律和突变特征（林杭等，2007；马宗源等，2010）。为了进一步验证两级抗滑桩对坡顶土体位移的控制作用，本文通过建立两级抗滑桩支护的有限元计算模型，分析了两级桩不同排距和排布位置对坡肩水平位移的影响，从而进一步分析得出其控制效果，同时分别建立了坡顶存在建筑物浅基础和深基础的计算模型，探讨了浅基础离边坡的安全距离及深基础对边坡稳定性的影响。

1 模型建立及模型参数

工程中的高边坡通常上层为土体，下层为岩层，抗滑桩各参数对边坡稳定性的影响强弱各不相同，桩间距影响最大，其次是截面尺寸，最后是桩长（赵明华等，2010；朱泳等，2017；丁桥军和董铁斌，2020；何文野等，2020）。因此建立有限元计算模型如图1所示，具体尺寸如表1。边坡坡度为1.0 ∶1.5，一、二级抗滑桩分别嵌固在硬岩中，嵌固深度均是5.0 m。假定每根桩独立承受桩间土体压力，因此模型宽度为S。桩和岩土体的物理力学参数如表2 所示，土体服从摩尔库伦准则且为非关联流动法则的理想弹塑性本构模型。可视硬岩及抗滑桩为理想线弹性体，桩与土及岩体的摩擦系数分别取0.4（约为tan（0.75φ））和0.5。

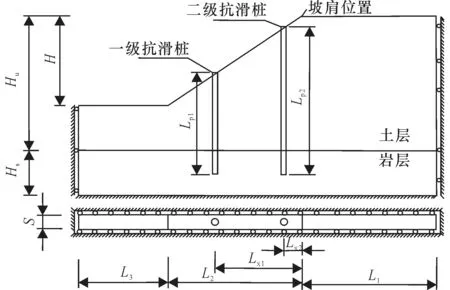
图1 两级抗滑桩—边坡模型示意图

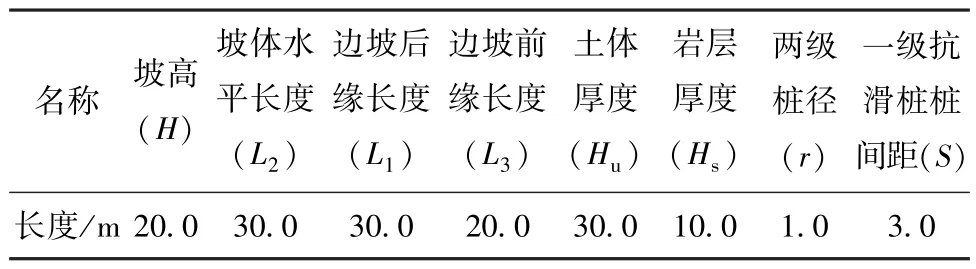
表1 高边坡模型尺寸及边界参数

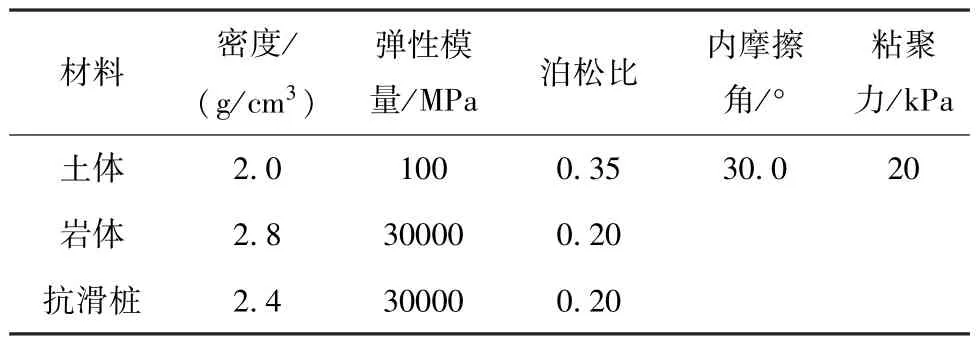
表2 桩和岩土体的物理力学参数

2 两级抗滑桩位置变化对坡肩水平位移的影响

2.1 一级抗滑桩的影响

为分析一级抗滑桩产生的坡肩水平位移影响，固定二级抗滑桩的位置，并保持二级抗滑桩设计参数不变。通过调整一级抗滑桩布设位置，改变一级和二级抗滑桩级距D。调整过程中一级抗滑桩的嵌岩深度保持不变，各计算工况模型参数如表3 所示，经验算各工况边坡整体稳定，下文仅对变形进行研究。计算结果如表4 所示。

（1）当边坡支护选用两级抗滑桩的形式，边坡坡肩的水平位移最大，一级桩水平位移最小，二级桩桩顶的水平位移介于两者之间。

（2）固定二级抗滑桩位置，当一、二级抗滑桩桩级距D增大时，坡肩水平位移增大，一、二级抗滑桩水平位移也同样增大。

（3）随着两级抗滑桩级距D的增加，坡肩水平位移和二级桩水平位移增加较大，一级桩桩顶水平位移增加稍小一些，可以看出在两级抗滑桩之间存在着一定的遮蔽作用。

（4）保持二级抗滑桩位置不变，调整一级抗滑桩的位置，坡肩位移从8.60 mm 增加到12.35 mm，位移增加量仅为3.75 mm，可以认为一级抗滑桩对坡顶土体位移有影响，但影响不显著。

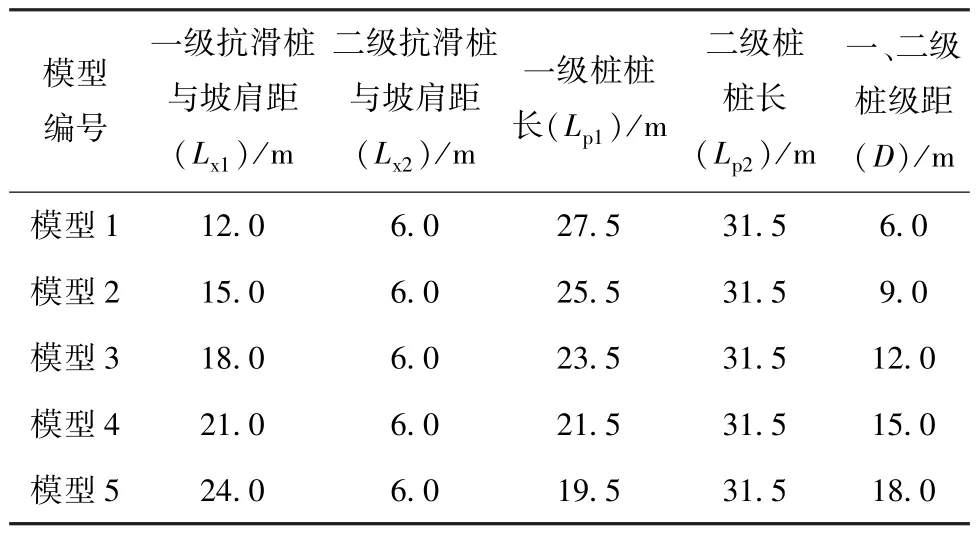
表3 模型几何参数

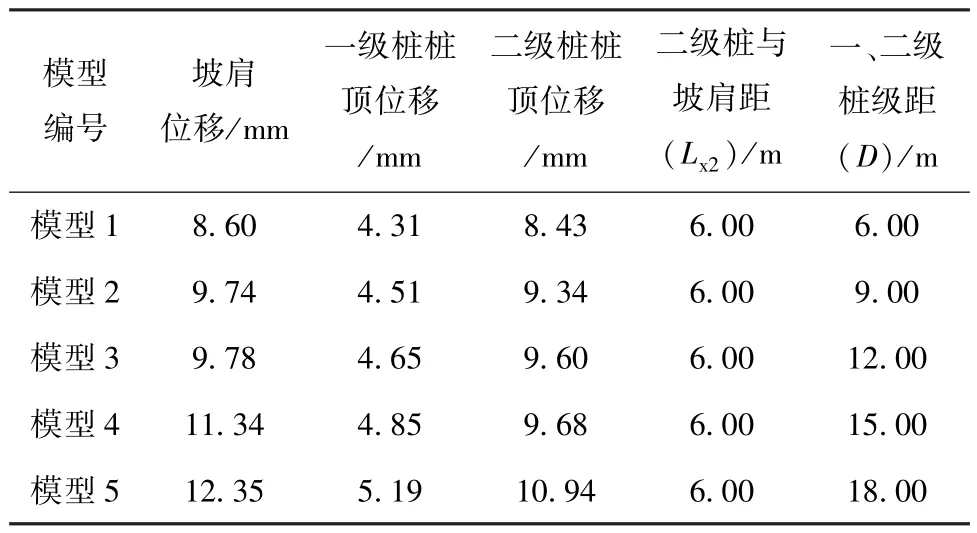
表4 坡肩及桩顶水平位移

2.2 二级抗滑桩的影响

由前文分析可得，一级抗滑桩产生的对坡肩水平位移影响不明显，因此在分析二级抗滑桩的影响时，应当使一、二级抗滑桩桩级距D保持不变（D=12.0 m）。各计算工况模型参数如表5 所示，经验算各工况边坡整体稳定，下文仅对变形进行研究。

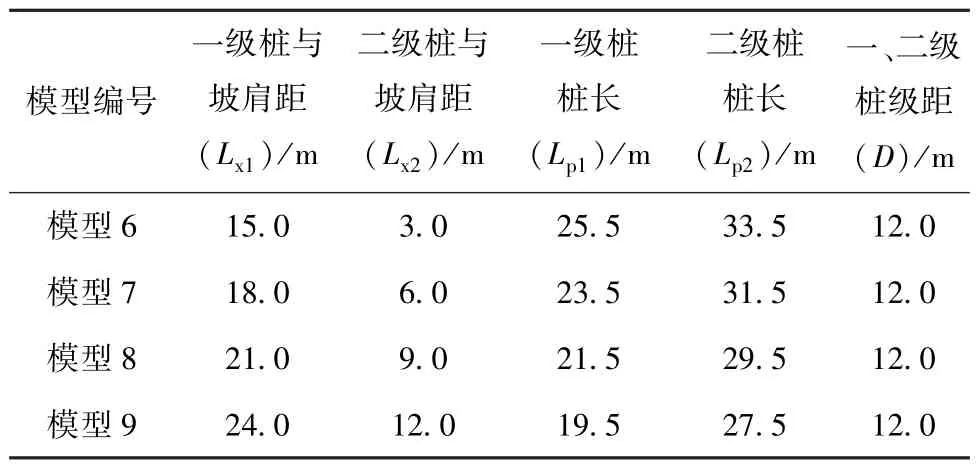
表5 模型尺寸

计算结果如表6 所示，由表6 可知：

（1）当一、二级抗滑桩桩级距D保持不变，二级抗滑桩距离坡肩水平位置Lx2增大时，坡肩水平位移随之而增大；一、二级抗滑桩桩顶水平位移同样随之增大；

（2）对比可得一、二级抗滑桩的布设位置更显著地影响了坡肩水平位移，而坡顶土体位移主要受到二级抗滑桩控制；

（3）由于二级抗滑桩的遮蔽作用，一级抗滑桩的桩顶位移量较小，且对坡肩的水平位移影响不显著，在有位移控制要求的边坡支护工程中，一级抗滑桩的布设可更多地考虑对坡脚位移地控制。

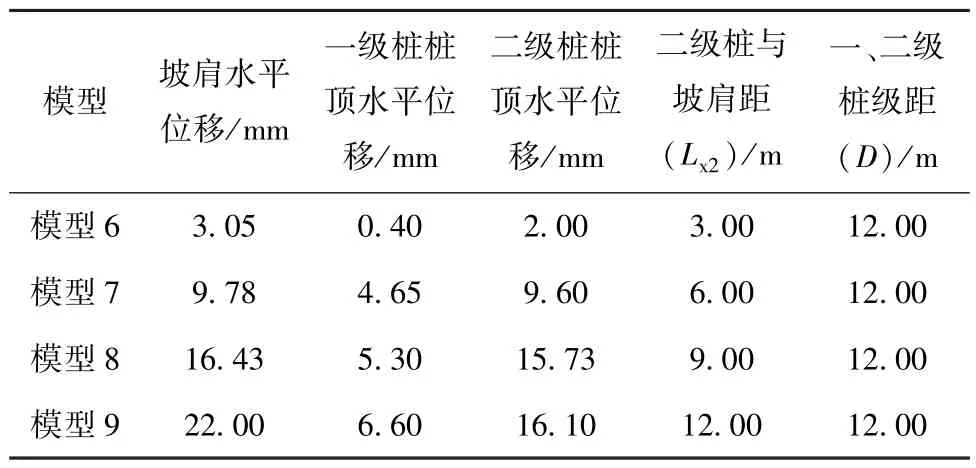
表6 坡肩及桩顶水平位移

3 坡顶存在不同类型基础的安全控制

3.1 坡顶浅基础的安全距离

如边坡坡顶存在浅基础，坡顶土体发生位移后，会对浅基础产生不利影响。为了得出在坡顶的建筑物与边坡的安全距离，在模型中取L1=40.0 m（边坡后缘长度），其他参数不变。另把坡顶浅基础建筑物荷载转化为三层砖混结构房屋所产生的荷载，确定其均布荷载=6×104Pa，选取3.0 m×3.0 m 范围，相邻基础间距3.0 m，对两跨均布荷载分析，如图2 所示。

由表可知2，土体弹性模量值取100 MPa，压缩模量与弹性模量不在一个数量级上，故该土体为中、低压缩性土。依据规范（中华人民共和国建设部，2011），中、低压缩性土砌体承重结构基础的局部倾斜为0.002，局部倾斜即是相邻基础沉降差比上它的距离，计算公式如下：

式（1）中：S1-S2（相邻基础的沉降差）；l（相邻基础中心点距离）。

平移边坡坡顶荷载，根据（1）式确定的局部倾斜值，经过一系列的调整，确保建筑基础局部倾斜接近0.002，则安全距离为坡肩至基础边缘距离，如表7 示。坡顶地表沉降曲线如图3、4 所示。

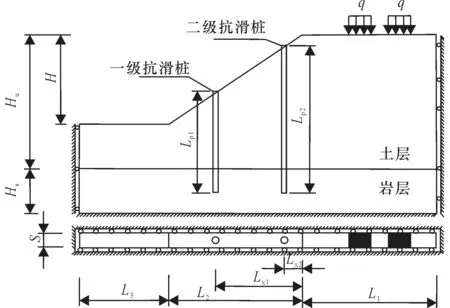
图2 坡顶存在浅基础模型示意图

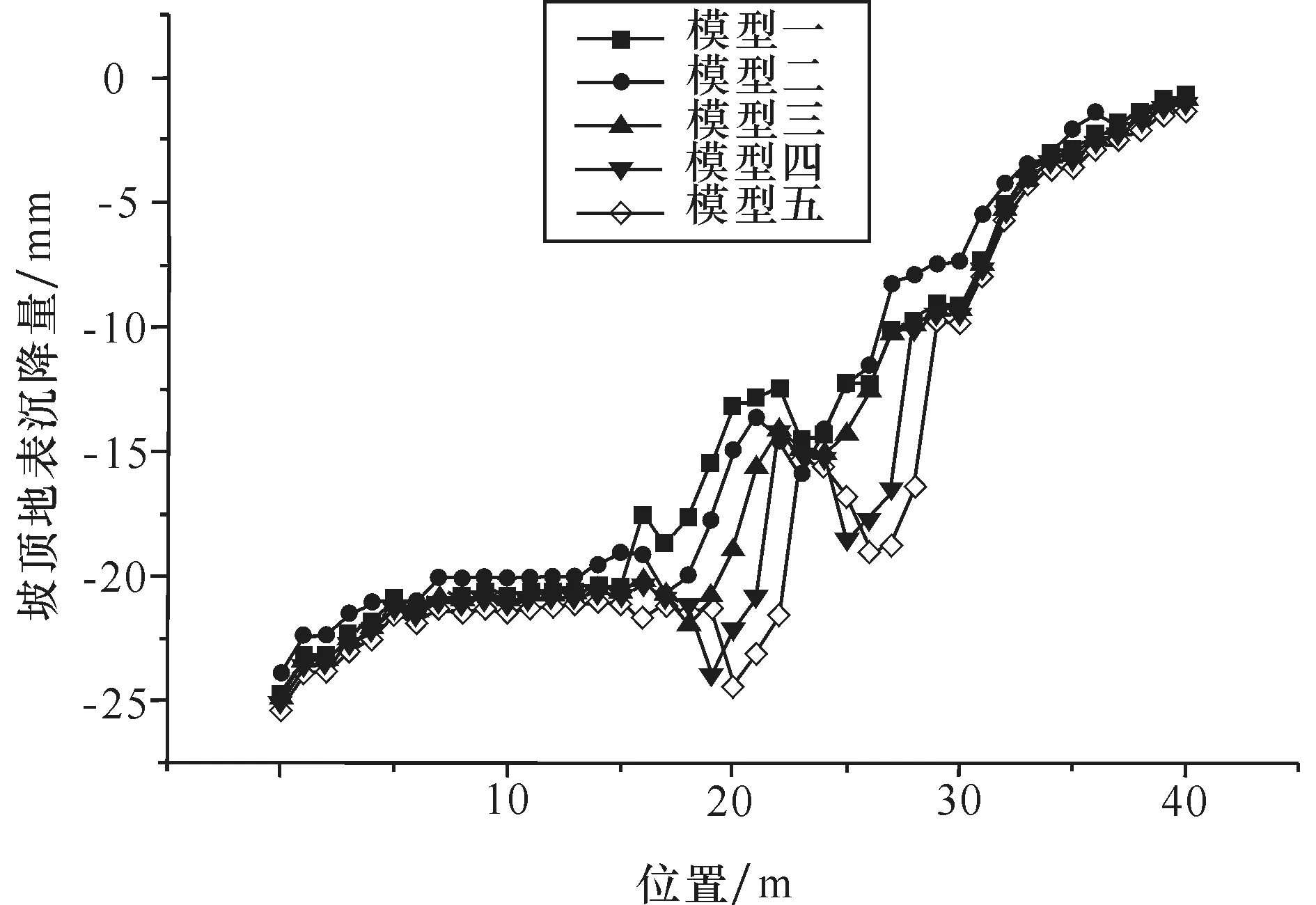
图3 模型（1～5）坡顶地表沉降量

由图3、4 可得，地表沉降量在边坡坡肩边缘线上是最大的，最大能达到30.00 mm 左右。且离坡肩边缘线越远，沉降量越小。与周边地区的地表沉降相比，浅基础荷载作用区域更大，由于两处浅基础荷载与坡肩距离不同，存在明显的沉降量差。由表7 可得，在6×104Pa（3.0 m×3.0 m）的均布荷载作用下，边坡坡肩水平位移越大建筑物所需安全距离也越大，因此临近边坡的建筑物一定要确保在安全距离以外，必须严格控制边坡坡肩水平位移。在设计两级抗滑桩时，则应在保证边坡整体稳定性前提下，尽量将二级抗滑桩布设在距离坡肩位置距离较近处，有效降低坡顶土体的位移量，而一级抗滑桩的布置更多地考虑边坡的局部稳定性和坡脚位移控制。

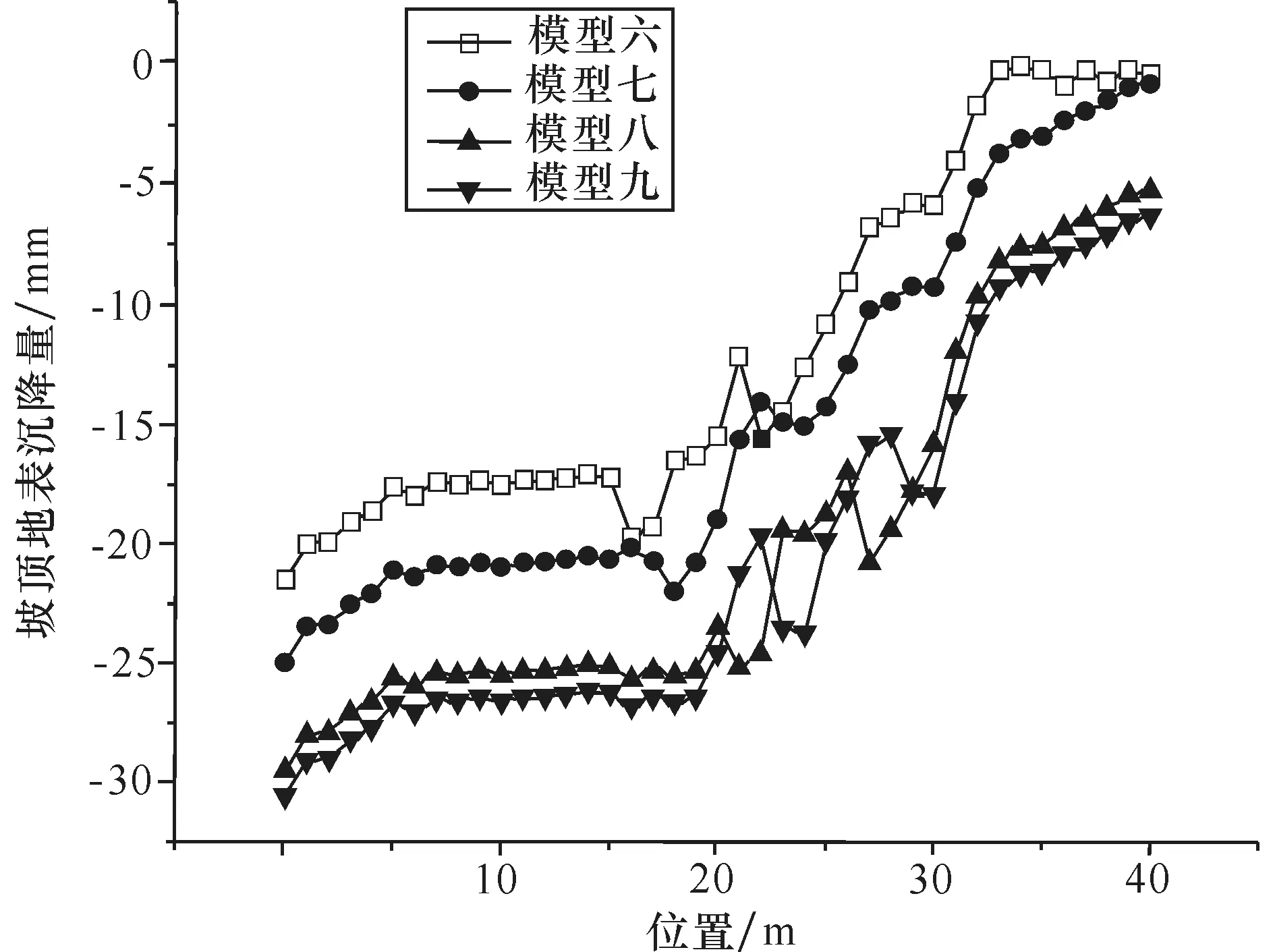
图4 模型（6～9）坡顶地表沉降量

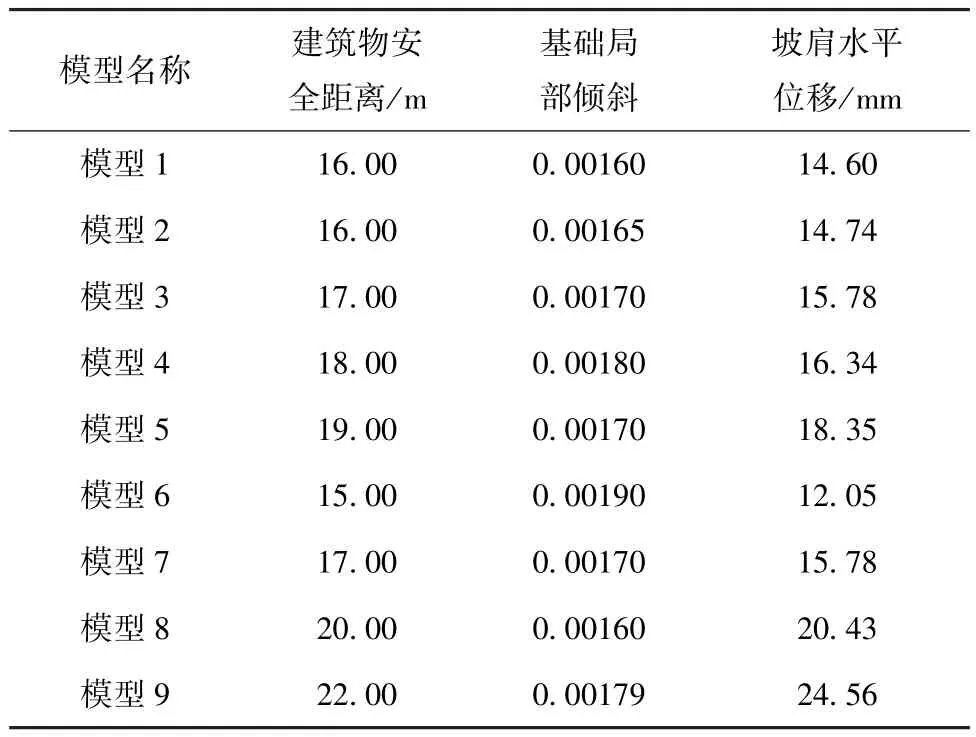
表7 建筑物安全距离

3.2 坡顶上的桩基对边坡稳定性的影响

深基础虽然能更好地控制建筑基础不均匀沉降，但当桩基位于边坡坡顶附近时，建筑通过桩基将荷载传递到周围土体，可能会对边坡稳定性造成不良影响。考虑桩基距离边坡的距离和所承受垂直荷载和水平荷载，建立如下有限元计算模型。

模型的尺寸与边界条件如图5 所示，具体尺寸如表8。

表8 坡顶桩基模型的尺寸与边界参数

另取边坡坡度为1.0 ∶1.5，一、二级桩径1.0 m，同级桩桩间距S为3.0 m。建筑物桩径1.0 m，桩长25.0 m。W是桩基坡肩距。所选材料同表1，建筑物桩基与抗滑桩物理力学参数取值一致，桩基与土的摩擦系数也取为0.4。采用折减系数法，以坡肩水平位移出现拐点对应的折减系数作为边坡在不同工况下的稳定系数。

分别改变计算模型中W、作用在桩基上的垂直荷载及水平荷载，研究这些因素对两级抗滑桩边坡稳定性的影响。初始模型中W取为10.0 m，有800 kN 垂直荷载以及从右到左沿着边坡滑动方向的100 kN 水平荷载作用在桩基上。图6 中边坡稳定系数与W关系曲线为只改变桩基距离坡肩的距离W，保持垂直荷载和水平荷载不变。同理，图7 为只改变桩基所承受的垂直荷载，图8 为只改变桩基所承受的水平荷载。

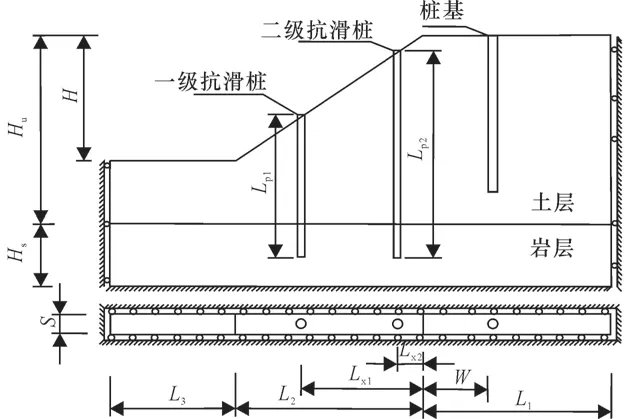
图5 坡顶存在深基础的模型示意图

由图6～8 分析可知：

（1）荷载相同时，边坡稳定系数随W减小而减小。既桩基距离边坡坡肩越近，对边坡的稳定性越不利。

（2）桩基位置和所受水平荷载不变时，边坡稳定系数在1.18～1.23 之间变化，变化范围不超过5%，桩基所受垂直荷载对边坡稳定性影响较小。

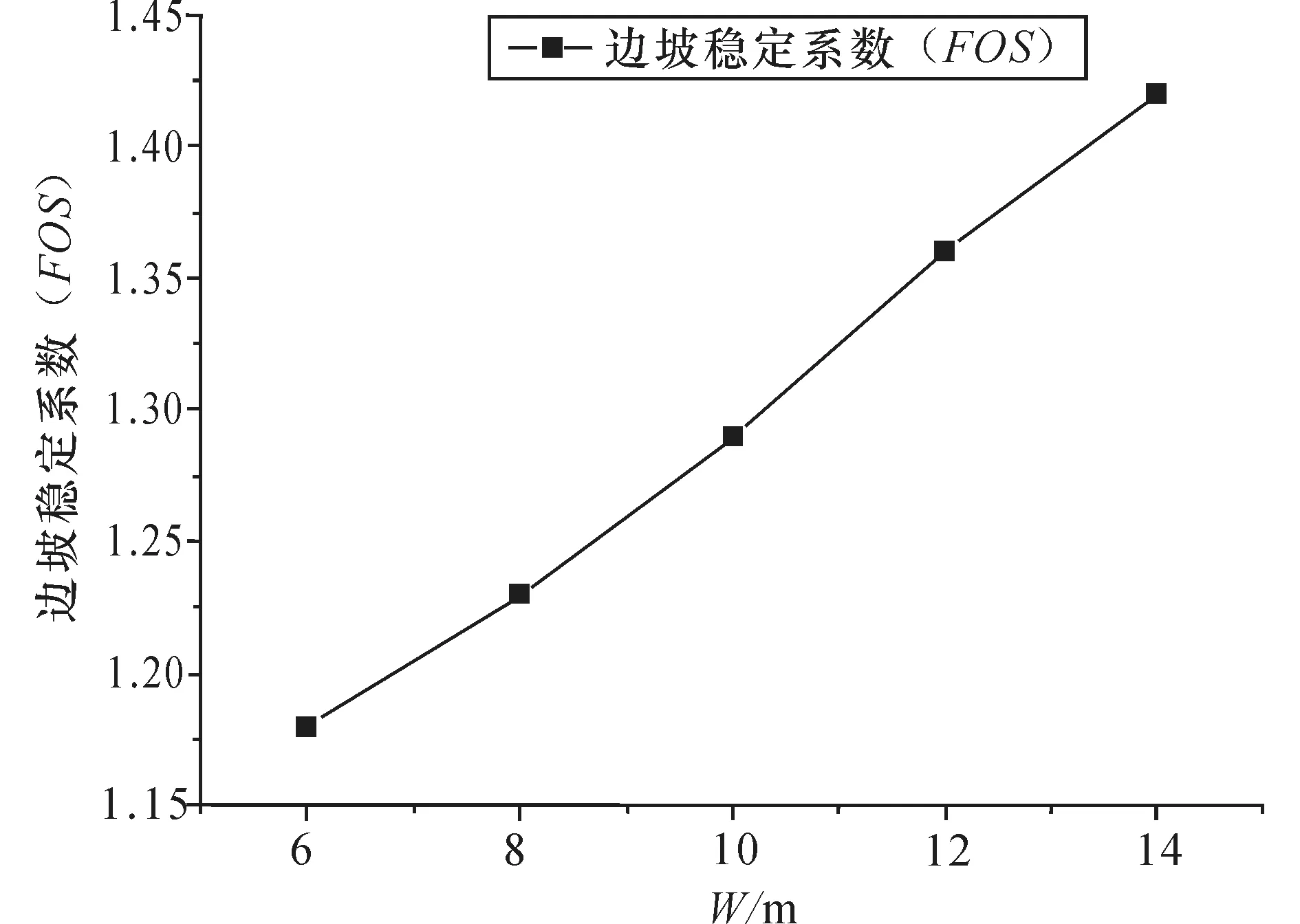
图6 边坡稳定系数与W 的关系

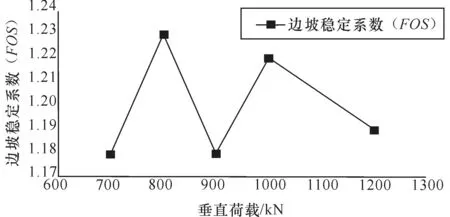
图7 垂直荷载与边坡稳定系数的关系

图8 水平荷载与边坡稳定系数的关系

表9 某边坡模型尺寸及边界参数

（3）桩基位置和所受垂直荷载不变时，随水平荷载增大边坡稳定系数减小。既沿边坡滑动方向的水平荷载会对边坡的稳定性产生不利影响。

4 工程实例

广西梧州市半山豪庭工程位于梧州市长洲区蜈蚣山脚下，其边坡位于该市地质灾害易发区，西侧边坡曾多处滑坡。最终该地块形成的高切坡达12～30 m，且地质条件较复杂。本文选取了4-4′主滑面剖面作为研究对象，工程地质剖面图如图9 所示。

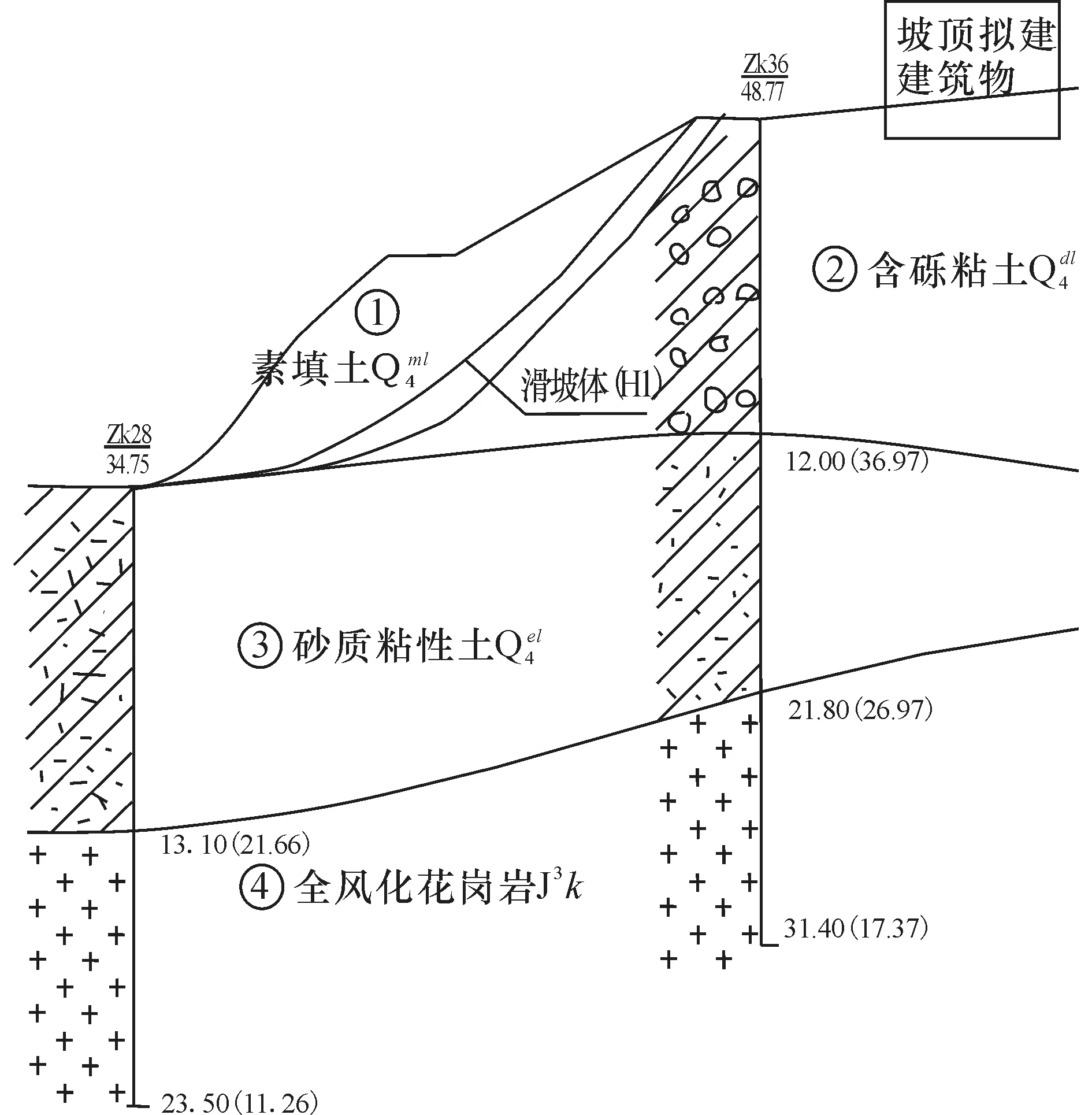
图9 4-4′主滑面工程地质剖面图

由地质剖面图可知，H1滑坡治理后拟在坡顶修建建筑物，在对滑坡进行治理后，必须良好控制滑坡后方土体位移，保障建筑的安全和稳定，因此本工程采用两级抗滑桩的支护形式，根据上文分析结果，在保障边坡稳定的基础上，尽可能将后排抗滑桩布置在距离H1滑坡坡肩较近处。最终根据现场实际施工条件等进行设计，两级抗滑桩的参数：坡肩与一、二级抗滑桩距离Lx1=18.0 m、Lx2=3.0 m，桩端嵌入花岗岩中，一、二级抗滑桩桩长Lp1=18.5 m、Lp2=26.5 m，桩径=1.2 m，两级抗滑桩桩间距都取3.0 m。

根据以上设计参数，建立该处边坡的有限元计算模型。为简化计算，划分三层岩土层，底层是花岗岩，中层是砂质粘土，上层是含砾粘土，如图10 示，模型尺寸如表9。另取桩径=1.2 m，桩间距S=3.0 m，边坡坡度为1.0 ∶1.5。抗滑桩和花岗岩选用理想弹性模型，土体采用摩尔库伦模型，材料参数见表10。

工程施工结束后，对前、后排桩桩顶水平位移和坡肩水平位移进行了监测，并与有限元模型计算结果进行比较，如表11 所示。

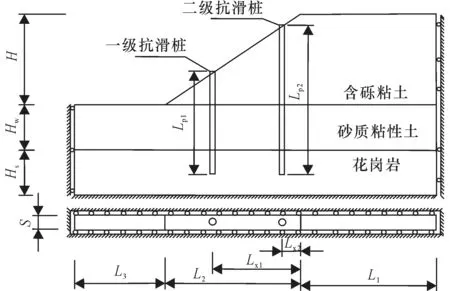
图10 计算模型尺寸与边界条件示意图

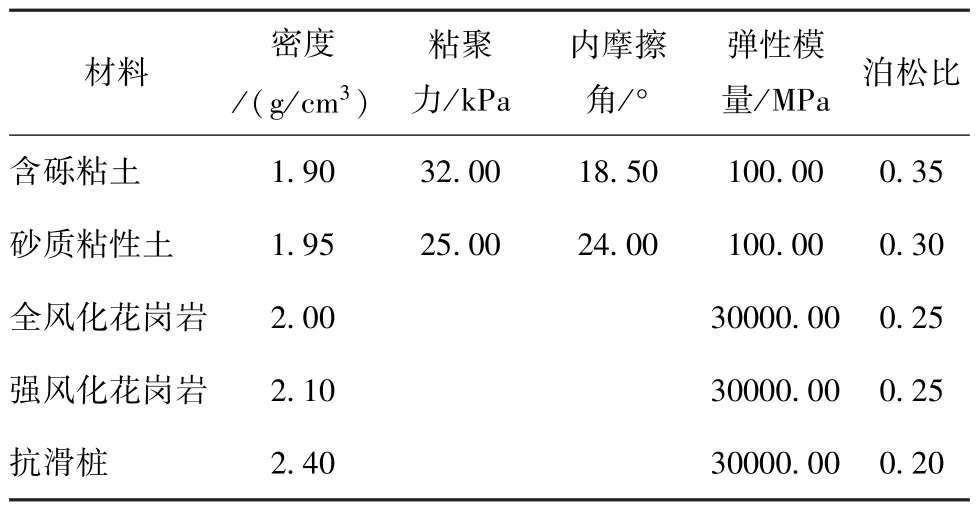
表10 模型力学参数

表11 一级、二级和坡肩水平位移对比

有限元模型计算结果与实测结果吻合较好，坡肩水位位移最大，但通过合理布置两级抗滑桩的位置，实测坡肩水平位移仅为12.5 mm，说明边坡后方土体位移较小，良好地保证了后方地下室等构筑物的稳定和安全正常使用。

5 结论

（1）采用两级抗滑桩的支护形式，边坡的坡肩水平位移最大，一级抗滑桩桩顶水平位移最小，二级抗滑桩桩顶水平位移介于两者之间。

（2）一级抗滑桩对于坡顶土体位移存在影响，但不显著，主要由二级抗滑桩控制坡顶土体位移，且二级抗滑桩距离坡肩越近，坡顶土体位移越小。

（3）边坡坡肩水平位移越大，坡顶浅基础的建筑物安全距离也越大。坡顶浅基础越是临近边坡，对土体位移的控制要求越大。

（4）桩基距离边坡坡肩越近，对边坡的稳定性越不利。相对于桩基所受垂直荷载，水平荷载对边坡的稳定性影响更显著。

（5）根据两级抗滑桩对坡顶土体的位移控制规律，对广西某滑坡进行了优化设计，最终实测结果表明双排抗滑桩对桩顶土体位移控制效果良好。

致谢论文撰写，充满艰辛。首先，我最想感谢的是总能及时地在学业上为我提供无私帮助的导师范秋雁教授。其次感谢李天雨，梁家珲，唐峰，韩伟，李拓，陆明，韩进仕，张备，黄伟，李武奇以及杨鹏帅等诸位师兄，感谢他们给予的指导和帮助。感谢同门何伟，周金，秦阔。此外，要感谢我的父母和亲人。

最后特别感谢百忙中抽出时间给予宝贵意见和专业指导的编辑部及审稿的专家、教授们。