带惩罚的无容量设施选址问题的降阶回溯算法

苟海雯，宁爱兵，胡 沁，张惠珍

上海理工大学 管理学院，上海200093

1 引言

设施选址问题（Facility Location Problem，FLP）是运筹学、理论计算机科学和管理科学中一类非常重要的组合优化问题，受到了广泛而深入的研究[1-4]。该问题在实际生活中有着非常重要的应用，如医院、消防站、超市、无线通讯网络基站和自动取款机等位置的确定[2]。在无容量设施选址问题（Uncapacitated Facility Location Problem，UFLP）中，每个顾客的需求都必须得到满足；然而在某些实际情况下，某些顾客的需求不一定必须得到满足[5]，引入对每个顾客惩罚的概念，对没有被满足需求的顾客，将会造成一定的损失，即惩罚费用，在UFLP的基础上考虑这个因素，将它添加到UFLP的一般模型中，于是就得到了UFLP 的一个变形问题，即带惩罚的无容量设施选址问题（Uncapacitated Facility Location Problem With Penalties，UFLPWP）[6]，其目标是选择给定设施集合的一个子集，开设该子集中的设施，决定对哪些顾客提供服务，对哪些顾客不提供服务而选择被惩罚，最终使得设施的开设费用、顾客与设施之间的连接费用和支付的惩罚费用之和最小。

UFLPWP是组合优化中NP-Hard问题，除非P=NP，否则不存在多项式时间的精确算法。目前解决NPHard问题的算法主要分为三类：精确算法、近似算法和启发式算法。虽然近似算法能够在多项式时间内得到一个常数近似比的解，但缺点是无法求得问题的最优解；启发式算法的求解速度相对较快，但缺点是容易陷入局部最优解，因此近似算法和启发式算法都无法保证得到问题的全局最优解；目前的精确算法虽然能求得问题的最优解，但缺点是没有研究问题本身的数学性质，因此求解速度相对较慢。本文针对以上缺点，首先研究UFLPWP 的数学性质，并进行了相应的数学证明，利用这些数学性质可以对问题进行降阶进而缩小问题的规模；然后在此基础上设计了基于上、下界的一种精确算法来求解UFLPWP，本文的数学性质不仅可以应用于本文设计的算法，还能广泛应用于其他各种算法，达到加快精确算法及其他算法求解速度的目的。

2 文献综述

UFLPWP最先是由Charikar等[7]开始研究的，Charikar等[8]针对UFLPWP的惩罚函数类型和特征，根据对偶规划原则，基于保证可行性的前提下，得到问题的对偶可行解，结合惩罚性设计了基于原始对偶技巧的近似算法，起到了加快问题求解速度和得到有质量保证解的作用，得出算法的近似比为3；后来，Xu[9-10]针对UFLPWP的整数线性规划模型，研究了UFLPWP的可度量性，即距离满足非负性、对称性和三角不等式，设计了基于线性规划舍入技巧的近似算法，加快了UFLPWP 的求解速度，得出算法的近似比为（2+2/e）；随后利用费用收缩和贪婪算法，将两者相结合，又将近似比改进到了1.852 6；此外，Hayrapetyan等[11]设计了基于线性规划舍入技巧的(1+ρ)近似比的算法。

以上文献综述中的近似算法能够在多项式时间内求得一个常数比的近似解，但缺点是不能求得问题的最优解，本文针对文献中近似算法的不足，设计了一种能够求得最优解的精确算法，对UFLPWP 的整数线性规划数学模型进行研究，对问题的求解特性进行数学分析，得出能加快问题求解速度的数学性质，在此基础上设计一种降阶回溯算法来求解UFLPWP。

3 问题分析与模型构建

3.1 问题分析

UFLPWP 是UFLP 的变形问题之一，与UFLP 的不同在于，在UFLPWP中，某些顾客的需求不一定必须被满足，对没有被满足需求的顾客j∈C，将造成一部分费用损失，即惩罚费用；对被满足需求的顾客j∈C，必定与开设的设施相连接，并由其提供服务，将产生设施的开设费用和顾客与设施之间的连接费用。UELPWP的目标是选择给定设施集合F的一个子集R，开设R中的设施，且选择被惩罚的顾客集合，将没有被惩罚的顾客连接到一个开设设施上（即为没有被惩罚的顾客提供服务），最终使得设施开设费用、顾客与设施之间的连接费用和支付的惩罚费用之和最小。

3.2 数学模型

在UFLPWP 中，给定设施集合F，顾客集合C，对于任意的i∈F,j∈C,fi表示设施i开设的开设费用，cij表示设施i为顾客j提供单位服务量所需支付的连接费用，pj表示顾客j∈C被惩罚的惩罚费用，也就是说当顾客j没有被服务时，需要支付的惩罚费用为pj。其中，设施总个数为m，顾客总个数为n，对每个设施i∈F是否开设引入0-1变量yi，对顾客j∈C是否连接到设施i∈F上引入0-1 变量xij，对顾客j∈C是否被惩罚引入0-1变量zj。最终使得设施开设费用顾客与设施之间的连接费用和支付的惩罚费用三项之和达到最小。

于是，UFLPWP 可以用下面的0-1 线性规划模型来表示：

在上述0-1 线性规划模型中，yi表示设施i∈F是否开设，若设施i∈F开设，则yi=1，否则yi=0；xij表示顾客j∈C是否与设施i∈F相连接，若相连接，则xij=1，否则xij=0；zj表示顾客j∈C是否被惩罚，若被惩罚，则zj=1，否则zj=0。目标函数（1）表示在满足全部约束条件下，最小的设施开设费用、连接费用以及支付的惩罚费用之和；约束条件（2）保证了顾客j如果没有被惩罚，那么它肯定与一个设施相连并由其提供服务；约束条件（3）表示顾客j只能与开设的设施相连并由其提供服务。

4 算法设计与分析

4.1 数学符号及解释

为了便于描述，采用以下数学符号表示。

m：设施总个数；

n：顾客总个数；

fi：开设设施i∈F的开设费用；

cij：设施i∈F为顾客j∈C提供单位服务的连接费用；

pj：顾客j∈C被惩罚的惩罚费用，即顾客j没有被服务时，需要支付的惩罚费用；

F={1,2,…,i,…,m}：设施集合；

C={1,2,…,j,…,n}：顾客集合；

F1：最优解中需要开设的设施集合，若F1中任一设施关闭则不能取得最优解，为全局变量；

F0：最优解中不能开设的设施集合，若F0中任一设施开设则不能取得最优解，为全局变量；

F5：F5=F/F1/F0，表示暂未确定是否开设的设施集合，为全局变量；

FF1：F5中的设施在回溯算法中假设开设的设施集合，为全局变量；

FF0：F5中的设施在回溯算法中假设关闭的设施集合，为全局变量；

Temp1：若设施h开设，则设施集合Temp1中的设施一定不开设，为全局变量；

Temp2：若设施h开设，则设施集合Temp2中的设施一定不开设，为全局变量；

S：服务集；

P：惩罚顾客集，不对集合P中的顾客提供服务；

min_cij：对于顾客j，连接到设施i上的连接费用在所有可能开设的设施中的连接费用是最小的，记最小的连接费用为min_cij；

C1：满足条件min_cij＜pj的顾客集合；

C2：满足条件pj＜min_cij的顾客集合。

4.2 数学性质

性质1若设施i的开设费用在所有设施的开设费用中最小，且为C1顾客集合中的顾客提供服务并且连接费用均是该顾客的最小连接费用min_cij，则设施i一定开设并为C1顾客集合中的顾客提供服务，且为该问题的最优解。

证明由该问题的数学定义可知，显然成立。

性质2若存在一顾客j的惩罚费用pj=+∞，则顾客j一定与某一设施i相连且被提供服务。

证明由于顾客j的惩罚费用pj=+∞，若顾客j不被提供服务即被惩罚，则会使总成本为+∞，所以顾客j一定与某一设施i相连且被提供服务。

性质3 若存在设施i,k，其设施开设费用fi＞fk，且对于任一顾客j连接费用都满足cij≥ckj，则称设施i相对设施k为严格劣势，则设施i一定关闭，即将设施i放入集合F0中，且删除设施i的关联边。

证明在UFLPWP 中，开设设施k比开设设施i更优，此时连接到设施i上的顾客都可以连接到设施k上且目标函数值更小，故性质3成立。

性质4 在开设设施未定的情况下，存在设施i，若顾客j连接到设施i的连接费用cij大于惩罚费用pj，即满足cij＞pj，则顾客j一定不连接到设施i上，且删除设施i与顾客j之间的连接边。

证明由于cij＞pj，因此顾客j连接到设施i上会使总成本更大，所以顾客j一定不连接到设施i上，且删除设施i与顾客j之间的连接边。

性质5 存在一设施i，设施i分别连接到顾客j1,j2,…,jk上的连接费用cij1,cij2,…,cijk均大于顾客j1,j2,…,jk的惩罚费用pj1,pj2,…,pjk,即满足cij1＞pj1,cij2＞pj2,…,cijk＞pjk，则设施i一定关闭，即将设施i放入集合F0中，且删除设施i的关联边。

证明用反证法。如果设施i开设，则必定有顾客与其连接并提供服务，由于cij1＞pj1,cij2＞pj2,…,cijk＞pjk，因此会使目标函数值更大，所以设施i一定关闭。

性质6 对于设施i，存在一顾客j，若同时满足下面2个条件：

（1）若fi+cij＜ckj，其中的k为除设施i之外的任一设施，该条件对每一设施k都成立。

（2）顾客j与设施i的连接费用cij与设施i开设费用fi之和小于顾客j的惩罚费用pj，即满足fi+cij＜pj。

那么设施i一定开设，即将设施i放入集合F1中，且客户j由设施i提供服务。

证明在UFLPWP中，顾客j要么被提供服务，要么被惩罚，由于fi+cij＜ckj，说明此时开设设施i能够使目标函数值更小，又由于cij+fi＜pj，说明此时顾客j与设施相连并被服务能使目标函数值更小，所以设施i一定开设且顾客j由设施i提供服务。

性质7 对于顾客j，求得min_cij，此时表示顾客j连接到设施i上的连接费用在所有可能开设的设施中的连接费用是最小的，其连接费用为min_cij；此时若设施i已经确定开设且min_cij＞pj，则顾客j一定被惩罚，即将顾客j放入集合P中。

证明由于设施i已经确定开设的情况下，且min_cij＞pj，因此顾客j连接到设施i上的费用比顾客j的惩罚费用大，且顾客j连接到设施i上的连接费用在所有可能开设的设施中的连接费用是最小的，因此顾客j一定被惩罚。

性质8 对于顾客j，求得min_cij，此时表示顾客j连接到设施i上的连接费用在所有可能开设的设施中的连接费用是最小的，其连接费用为min_cij；此时若设施i已经确定开设且min_cij＜pj，则顾客j一定被设施i服务。

证明由于设施i已经确定开设的情况下，且min_cij＜pj，因此顾客j连接到设施i上的费用比顾客j的惩罚费用小，且顾客j连接到设施i上的连接费用在所有可能开设的设施中的连接费用是最小的，因此顾客j一定被设施i服务。

性质9 若存在某一设施i，假如设施i不开设，且此时下界b大于全局的上界u，则设施i一定开设。

证明上界u小于下界b，说明此时关闭设施i不可能获得最优解，所以设施i一定开设。

性质10 若存在某一设施i，假如设施i开设，且此时下界b大于全局的上界u，则设施i一定不开设。

证明上界u小于下界b，说明此时开设设施i不可能获得最优解，所以设施i一定不开设。

性质11 若最优解中，设施g开设，假如存在设施h，对每一个客户j都满足cgj＜chj或pj＜chj，就把设施h放入集合Temp1；也就是说在设施g开设的情况下，集合Temp1中的设施必定不开设。

证明由于设施g开设，若存在设施h，若对每一个客户j都满足cgj＜chj或pj＜chj，那么要么客户j连接到设施g比连接到设施h上的成本小（当cgj＜chj），要么客户j接受惩罚的成本比连接到设施h上的成本小（当pj＜chj），因此不会开设设施h。

该性质可以用批量决定某些设施一定不开设。

性质12 若最优解中，设施g不开设，假如存在设施h，对每一个客户j都满足fg+cgj＜chj或pj＜chj，就把设施h放入集合Temp2；也就是说在设施g不开设的情况下，集合Temp2中的设施必定不开设。

证明由于设施g不开设，若存在设施h，若对每一个客户j都满足fg+cgj＜chj或pj＜chj，那么要么开设设施g且客户j连接到设施g比连接到设施h上的成本小（当fg+cgj＜chj），要么顾客j接受惩罚的成本比连接到设施h上的成本小（当pj＜chj），因此不会开设设施h。

该性质可以用批量决定某些设施一定不开设。

性质13 对于任一设施i，存在一顾客j，若顾客j与设施i的连接费用cij与设施i开设费用fi之和小于顾客j的惩罚费用pj，即满足cij+fi＜pj，则顾客j一定被提供服务。

证明由于cij+fi＜pj，即使开设设施i且把顾客j连接到设施i上的总成本比顾客j的惩罚费用小，因此顾客j一定被提供服务。

4.3 求解算法

4.3.1 上界和下界

（1）上界子算法

实际上，任何一个可行解对应的目标函数值均能作为该问题的一个上界，本文在前文提出的数学性质的基础上采用贪心算法的策略来设计上界子算法，算法主要步骤如下：利用前文提出的数学性质，对问题进行降阶处理，把确定不开设的设施以及与该设施相连接的边删除，之后开设与C1顾客集合中的每个顾客连接费用最小的设施作为一个可行解，此时开设的设施集合为Fu，对Fu中的每一个设施i做如下处理：

假设设施i不开设，令设施i服务的顾客集合为Cu，假设把Cu中的每一个客户j连接到集合(Fu/i)中连接费用最小的设施h(j)上；若满足：

若上述假设成立，则执行假设中的操作，此时对应一个目标函数更好的可行解，其对应的目标函数值作z即可作为UFLPWP的一个初始上界u。

（2）下界子算法

利用前文提出的数学性质对问题进行降阶处理，然后利用下面的公式计算下界b：

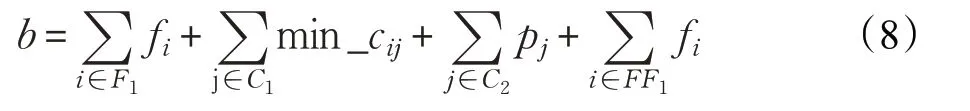
上式中，等式右边的第1项表示确定开设的设施集合F1中每一个设施的开设费用fi之和，第2 项表示C1顾客集合中每一个顾客的最小连接费用min_cij之和，第3项表示C2顾客集合中每一个顾客的惩罚费用pj之和，第4项表示回溯算法中假设开设的设施集合FF1中每一个设施的开设费用fi之和。

4.3.2 降阶回溯算法

此部分的算法由降阶子算法和回溯子算法两部分组成，降阶算法通过前文提出的数学性质进行降阶处理，进而缩小问题的规模；回溯算法采用深度优先策略，从根结点出发搜索解空间树，算法搜索至解空间树的任一结点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先策略搜索。本文的回溯算法从根结点出发，当搜索至解空间树的任一结点时，根据上下界子算法计算出的该结点的上界u和下界b，判断该结点的下界b是否小于上界u，若是，则继续向下深度优先搜索，否则进行剪枝处理，即跳过该结点及以下的子树，逐层向上级回溯。用present_c（简记为pre_c）来表示当前可行解的目标函数值，best_c来表示当前搜索到的最小目标函数值。

降阶子算法描述如下：

步骤1 初始化u=+∞,b=0,pre_c=0,best_c=+∞。

步骤2 利用前文的数学性质对该问题进行降阶处理，确定必定开设的设施，把确定必定开设的设施放入设施集合F1中；确定必定关闭的设施，把确定必定关闭的设施放入设施集合F0中；最后把剩下的不能确定是否开设的设施放入设施集合F5中；经过降阶处理后，可以得到两种情况：

（1）根据性质1得到问题的最优解，则算法结束。

（2）还没有得到最优解，则跳到步骤3。

步骤3 利用前文中的上下界子算法计算当前的上界u，且best_c=u，更新数组best_y与上界u对应的设施开设情况一致。

步骤4 对当前设施的开设费用按照非增排序，即此时的开设费用f1≥f2≥…≥fi≥…≥fm。

步骤5 调用回溯子算法Backtrack（1）。

回溯子程序Backtrack(i)算法描述如下：

步骤1 如果当i＞|F5|时，说明此时算法搜索至叶子结点，此时对应一个可行解，即得到一个确定开设设施的子集合F1，此时对应的目标函数值cur_c为确定开设的设施子集合F1开设费用之和加上顾客集合C1中(j∈C1)每一个顾客在F1上的最小连接费用之和，以及加上没有被连接的顾客惩罚费用之和，并将此时的pre_c与best_c比较，若pre_c＜best_c，则更新best_c=pre_c,u=best_c，数组best_y=y，该回溯子程序结束；如果当i≤|F5|时，则执行步骤2。

步骤2 利用二叉树来搜索最优解，在F5中取出开设设施费用最高的设施i，分两种情况处理：

（1）假设设施i开设，则执行步骤3。

（2）假设设施i关闭，则执行步骤5。

步骤3 假设设施i开设，利用性质11，可批量确定设施集合Temp1不开设，并设FF1=FF1∪{i},FF0=FF0∪Temp1,F5=F5/{i}/Temp1；此时利用下界子程序计算当前情况下的下界b1，若b1≥u，则该分支不存在更好的解，剪枝，跳到步骤4；若b1＜u，则先利用前文提出的数学性质对当前情况的问题进行降阶处理，然后再调用回溯子程序Backtrack(i+1)进入左子树。

步骤4 返回二叉树上一层之前恢复设置：FF1=FF1/{i},FF0=FF0/Temp1,F5=F5∪{i}∪Temp1。

步骤5 假设设施i关闭，利用性质12，可批量确定某些设施集合Temp2不开设，并设FF0=FF0∪{i}∪Temp2,F5=F5/{i}/Temp2；此时利用下界子程序计算当前情况下的下界b1，若b1≥u，则该分支不存在更好的解，剪枝，跳到步骤6；若b1＜u，则先利用前文提出的数学性质对当前情况的问题进行降阶处理，然后再调用回溯子程序Backtrack(i+1)进入右子树。

步骤6 返回二叉树上一层之前恢复设置：FF0=FF0/{i}/Temp2,F5=F5∪{i}∪Temp2。

算法结束后，当前的最优目标函数值best_c、对应的开设设施集合、被提供服务的顾客集合以及被惩罚的顾客集合就是整个问题的一个最优解。

4.4 算法的时间复杂度及对比分析

本文研究的问题规模即设施的个数为m，该算法在搜索空间树中最多产生2m个叶子结点，由于本文算法通过数学性质对问题进行了降阶处理，问题的规模减小为|F5|，令k=|F5|，因此算法在最坏情况下的时间复杂度为O(2k)。

针对设施选址问题，目前有三类算法可以解决此问题：近似算法[6，12]、启发式算法[13]和精确算法[14-15]。对于近似算法和启发式算法而言，虽然求解速度快，但是一般不能保证获得全局最优解，所以其解的质量不能保证。本文设计的降阶回溯算法是精确算法，所得到的解一定是全局最优解。对于一般的精确算法而言，没有针对问题进行数学分析，没有利用问题的数学性质对问题进行降阶处理，也没有考虑部分设施能够在多项式时间内确定其是否开设，所以算法的时间复杂度为O(2m)，由于本文的算法对问题进行了降阶处理，因此相对于本文的算法而言，其时间复杂度更高。本文的精确算法的优点在于首先研究了UFLPWP 的数学性质，然后根据其数学性质对问题进行降阶处理，从而减小问题规模，进而缩小了问题的解空间，因此算法仅对一部分设施进行搜索，降低了算法的时间复杂性，同时利用上下界子算法进行剪枝处理，只对子树进行搜索，提高了算法的求解速度。

5 算法应用及示例分析

为了更清楚地阐述本文算法的原理以及执行过程，下面给出一个示例来进行说明。

示例1 现有8个备选设施i，7个顾客j，从中选出若干个设施使其开设为顾客服务，同时选出被惩罚的顾客，且使设施的开设费用、顾客与开设设施之间的连接费用和支付被惩罚顾客的惩罚费用之和最小，即使总费用最小。设施的开设费用如表1所示，设施与顾客的连接费用如表2所示，顾客的惩罚费用如表3所示，总体示例如图1所示。

表1 设施的开设费用fi

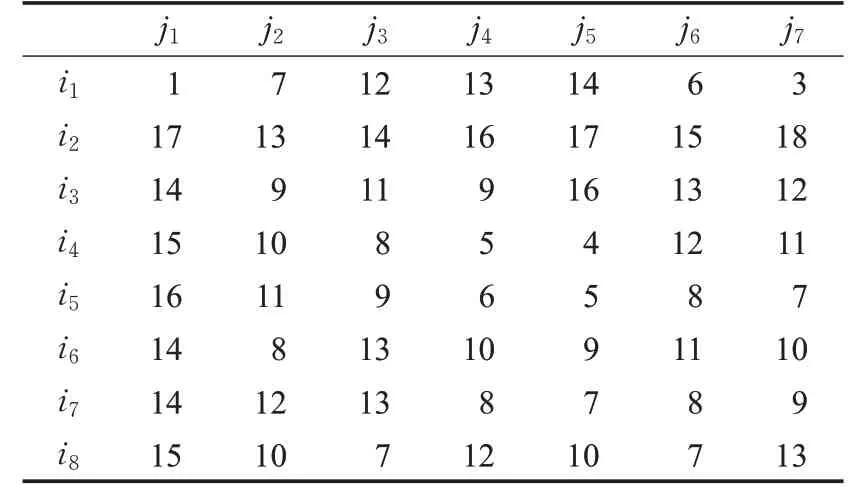
表2 设施与顾客的连接费用cij

表3 顾客的惩罚费用pj

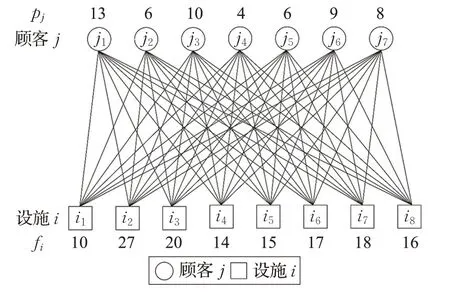
图1 示例1的图形表示

对示例1的求解分析过程如下：

（1）利用数学性质3，关闭设施i2，从图1 中删除设施i2，将设施i2放入集合F0中，同时删除各顾客与设施i2的连接边{i2j1,i2j2,i2j3,i2j4,i2j5,i2j6,i2j7}。

（2）利用数学性质4，对于顾客j1，可从图1 中删除边{i3j1,i4j1,i5j1,i6j1,i7j1,i8j1}；对于顾客j2，可从图1中删除边{i1j2,i3j2,i4j2,i5j2,i6j2,i7j2,i8j2} ，将顾客j2放入集合P中；对于顾客j3，可从图1中删除边{i1j3,i3j3,i6j3,i7j3}；对于顾客j4，可从图1中删除边{i1j4,i3j4,i4j4,i5j4,i6j4,i7j4,i8j4}，将顾客j4放入集合P中；对于顾客j5，可从图1 中删除边{i1j5,i3j5,i6j5,i7j5,i8j5}；对于顾客j6，可从图1 中删除边{i3j6,i4j6,i6j6}；对于顾客j7，可从图1中删除边{i3j7,i4j7,i6j7,i7j8,i8j7}。

（3）利用数学性质5，关闭设施i3，从图1 中删除设施i3，将设施i3放入集合F0中。

（4）利用数学性质6可知，设施i1必定开设，且顾客j1由设施i1提供服务，将设施i1加入集合F1中，将顾客j1与设施i1的连接边{i1j1}加入到服务集S中。

（5）利用数学性质8，顾客j6一定由设施i1提供服务，将顾客j6与设施i1的连接边{i1j6}加入服务集合S中，并从图1中删除边{i5j6,i7j6,i8j8}；顾客j7一定由设施i1提供服务，将顾客j7与设施i1的连接边{i1j7}加入服务集合S中，并从图1中删除边{i5j7}。

（6）由于设施i1已经确定开设，利用数学性质11，批量确定关闭设施集合Temp1={i6,i7}，并从图1中删除与设施i6,i7关联的所有边。

（7）通过数学性质降阶处理后，问题规模如图2 所示，计算当前情况的初始上界为u=56。

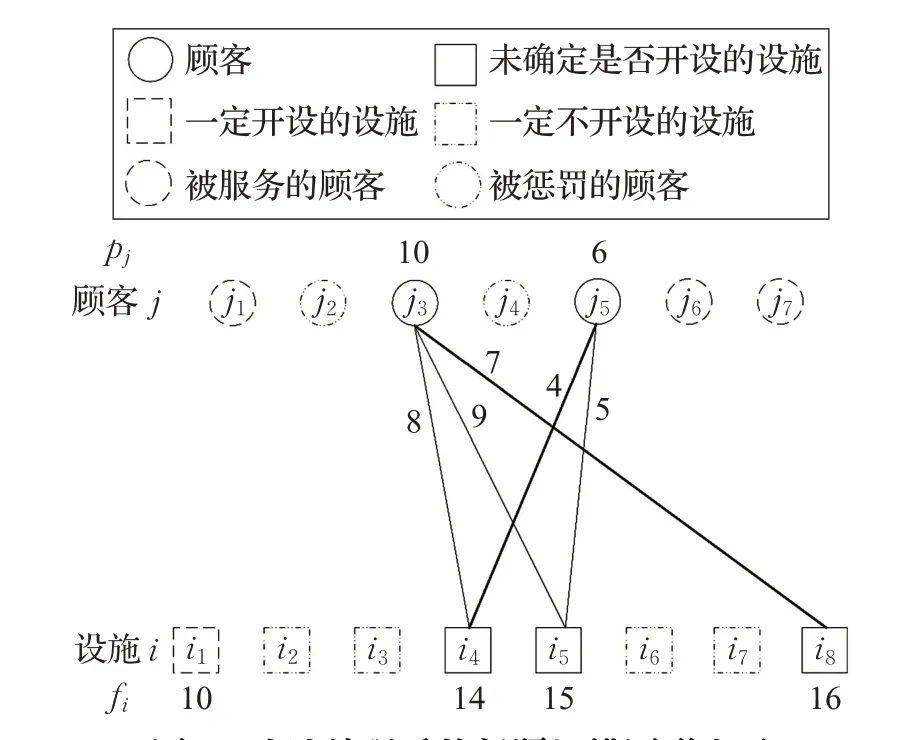
图2 降阶处理后的问题规模图形表示

（8）由于设施i1确定开设，对图2 中的设施i4、i5和i8按照费用fi非增排序f8＞f5＞f4。

（9）执行回溯算法对当前图进行处理，执行过程如图3。

通过上述算法可得到该问题的开设设施集为F1={i1},得到服务集S={i1j1,i1j6,i1j7},惩罚顾客集合为P={j2,j3,j4,j5}，最优目标函数值Z=46。采用本文设计的降阶回溯算法求解示例1，搜索树的叶子结点个数为23，若采用通常的精确算法求解示例1，则搜索树的叶子结点个数为28，若采用近似算法来求解示例1，则得到的解是常数近似比的解，不是全局最优解，若采用启发式算法求解示例1，容易陷入局部最优解，因此本文设计的算法与通常的精确算法、近似算法和启发式算法相比，本文的算法在求解的过程中减小了问题的规模，降低了算法的时间复杂度，加快了问题的求解速度，同时求出了问题的最优解。

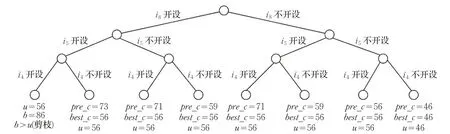
图3 搜索树

6 结论

本文研究了UFLP的变形问题之一，即带惩罚的无容量设施选址问题（UFLPWP），有如下创新点：（1）首先研究了UFLPWP的数学性质，并进行了数学证明，这些数学性质不仅可以应用于本论文设计的算法，还能广泛应用于其他各种算法；（2）利用这些数学性质可以对问题进行降阶进而缩小问题的规模；（3）然后在数学性质和降阶算法的基础上设计了基于上、下界的回溯算法来求解UFLPWP。通过对示例1求解过程分析可知，求解的时间复杂度为23与普通精确算法求解的时间复杂度28比有了很大程度的降低，减小了问题的规模，加快了问题的求解速度。