抽水蓄能机组甩负荷试验时尾水锥管压力
张 飞,王宪平
抽水蓄能机组甩负荷试验时尾水锥管压力
张飞1,王宪平2
(1. 国网新源控股有限公司技术中心,北京 100053;2. 上海福伊特水电设备有限公司,上海 200240)
抽水蓄能机组水力调节过渡过程计算控制核心要求之一是尾水锥管压力不超过设计值。设计值是根据水力过渡过程理论的一维数值模拟“计算值”加上一定“压力脉动修正”量和“计算误差”后计算获得。长期以来,尾水锥管压力计算值与尾水锥管压力测量值之间仍存在一定偏差,导致采用实测数据对计算结果进行评判时不能得到合理的解释与评价。为解决调节保证计算与试验验证之间的分歧,该研究对调节保证计算时尾水锥管压力最小值含义进行了阐释,梳理了调节保证计算与试验中涉及尾水锥管压力的相关国内标准。在此基础上,以洪屏抽水蓄能电站调试阶段四台机组甩额定负荷时的实测尾水锥管压力为研究对象,首先分析了压力测点的测量条件,采用短时傅里叶变换进行频率特性分析,验证了测试数据的有效性;其次采用Savitzky-Golay滤波器分离出了表征一维数值模拟断面平均压力计算值的压力趋势与表征流动复杂性的压力脉动,针对压力脉动项研究了峰峰值与时长的关系并获得了压力脉动项最大峰峰值,验证了趋势项与一维数值模拟之间的一致性;随后采用压力脉动项最大峰峰值对数值模拟和实测压力趋势项极值进行修正;最后总结形成了尾水锥管压力调节保证设计值的修正流程。案例研究表明:采用截止频率为0.1~0.2倍转频的低通滤波器可以有效分离出与一维数值模拟一致的尾水锥管压力趋势项;采用3~4个旋转周期数对应的压力脉动数据进行分析可以获得压力脉动项的最大峰峰值;利用压力脉动最大峰峰值对一维数值模拟极值进行修正能够实现调节保证的有效设计与验证。该研究为抽水蓄能机组调节保证设计与验证提供了有效支撑。
压力脉动;数值模拟;调节保证计算;尾水锥管压力;Savitzky-Golay滤波器
0 引 言
抽水蓄能机组调节保证设计值是抽水蓄能电站设计时的关键参数。抽水蓄能电站及机组设计过程时,上游管路承压显著大于下游管路,上游管路所受到的载荷相对简单,而下游管路则较为复杂,特别是尾水锥管段。输水系统中,极端情况下管路最大应力可能是水力共振现象所造成,但普遍是由甩负荷时产生的水击压力及其引发振动导致,因此对机组甩负荷时水力量测数据进行研究有助于揭示水力过渡过程下流道内压力特征,并实现对调节保证计算与设计的校验。
一维水力过渡过程计算时假定管道中水流为一元流动、不可压缩,断面内水力学参数无差异,不考虑水中含气量变化对水锤波速的影响,不考虑空化等[1],且所用特性曲线为模型试验获得,与真机存在差异[2]。因此,借助数学建模完成的一维水力过渡过程数值模拟所获得相应位置处的压力是断面平均压力。甩负荷后,锥管内部分空间存在空化现象[3],同时未发生空化区域的流动状态也非常复杂,存在一定程度的压力脉动,断面平均压力高于锥管内最低压力,故需要对一维数值模拟方法获得的数值进行适当修正,以获得标准所述的尾水锥管最低压力。
对具有长尾水输水系统的抽水蓄能电站,甩负荷时重要的是防止锥管内发生水柱分离-弥合现象。目前,已存在水柱分离-弥合隐患问题导致的非正常运行案例报道[4-5]。大量案例表明,基于特征线法的一维数值模拟方法对甩负荷工况进行预测时尾水锥管压力仿真值与实测曲线趋势吻合度较好,在趋势预测方面具有相当高的精度,Pejovic等研究表明,多数情况下一维数值模拟获得的最小值低于实测趋势最小值[6],这在很多工程实践中获得了验证。目前,利用基于特征线法的一维数值模拟计算结果对实测结果进行评价时,一维数值模拟结果是否需要修正、以及如何修正和修正多少存在争议,工程上尚未完全达成共识。有观点认为,工程上必须对一维数值模拟结果进行修订[6]。但由于锥管内复杂的流动状态,导致极值修订存在很大偏差,这一偏差目前并未获得基于原型机组试验数据的有效案例支撑;同时考虑到工程实践,只能通过接近锥管管壁压力测量对压力极值进行评价,因此对锥管管壁压力数据进行分析是极为必要的。
目前,中国规程规范中关于抽水蓄能电站调节保证设计共涉及4个标准,分别是:《关于印发水电站输水发电系统调节保证设计专题报告编制暂行规定(试行)的通知》(水电规机电[2013]12号)[7]、T/CEC 5010-2019《抽水蓄能电站水力过渡过程计算分析导则》[8]、NB/T 10072-2018《抽水蓄能电站设计规范》[9]和DL/T 5186-2004《水力发电厂机电设计规范》[10]。分析得出各规范之间无差异,尾水进口断面均要求最低压力值不小于−0.08 MPa。因此,目前的行业共识是,调节保证验证时,保证工况下锥管管壁的实测压力最小值应不小于−0.08 MPa,此时认为机组是安全的。需要强调这是一种折中方法,并不能够保证锥管内不发生空化现象。
已有研究表明:水轮机非设计工况下,尾水锥管内存在多种形式的涡,如部分负荷下偏心涡带[11],超负荷情况下柱状空腔涡带[12]等,涡带的存在使锥管内流态复杂化。除设计工况外,锥管内水流呈螺旋状流动,断面内压力分布均大致呈“V”型分布[13]。理想情况下,压力传感器齐平安装于锥管管壁,不考虑压力脉动时,传感器测量所得到的是该断面内径方向上某一时刻的最大值,即:传感器所测随时间变化的压力趋势项是测量截面半径方向上压力分布最大值的包络线。这导致即使测量获得的压力值比较大,而实际锥管轴心线附近的压力已经达到空化压力。空化压力与汽化压力不同[14],考虑到抽水蓄能电站站址条件水质条件一般比较好,通常认为两者等同。故不能通过锥管管壁压力测量结果判断甩负荷后锥管各断面内的压力是否大于−0.08 MPa;同时锥管管壁处的压力脉动并非锥管内压力脉动最大的点,因而亦不能通过锥管管壁的压力脉动评估实际锥管内的压力脉动。但这并不表明不能通过锥管管壁处的压力测量评估锥管工作情况,因为锥管管壁处的压力及其脉动是锥管性能劣化的直接原因。
水泵水轮机甩负荷时锥管内不应发生较大的水柱分离-弥合现象,否则锥管内产生的强大冲击压力将造成机组及输水系统破坏。模型试验[3]及模拟仿真[15-17]均表明:甩负荷时锥管内不可避免产生空化现象,形成低频涡带,关键是控制空化腔体积不超过一定范围或截面内空化腔面积远小于发生空化位置处截面面积,从而避免水柱分离-弥合现象发生。水柱分离并不产生很大破坏,但是某些特殊工况下,其弥合过程可能产生极大的冲击,是造成压力突变、机组抬机、输水系统破坏等现象的主要原因。当进行调节保证设计时,标准要求尾水管内最小压力不小于−0.08 MPa时,其所述本质是尾水管内不发生水柱分离-弥合现象。
水泵水轮机锥管管壁处压力准确测量要求采用与管壁齐平安装传感器的方法。一些电站由于种种原因,并未齐平安装传感器,而采用引水管路方式测量。从理论和实践角度,采用引水管路引至某一高程后进行压力测量的方式不满足标准要求[18-19],数据不能真实反映被测位置处压力情况[20]。洪屏抽水蓄能电站在尾水锥管上设置了验水阀,本文借助时频分析技术分析表明该位置处测量近似满足测量条件。基于此,针对工程上尾水锥管压力实测数据缺乏有效分析方法,以及调节保证计算结果与实测数据验证之间缺乏校验方法问题,本文系统分析洪屏电站调试阶段四台机组甩额定负荷实测尾水锥管压力数据,采用Savitzky-Golay滤波器分离压力趋势和压力脉动,并验证压力趋势与一维数值模拟结果的一致性,总结调节保证所需要叠加的压力脉动。
1 试验概况与方法
1.1 电站基本参数
洪屏电站安装四台额定出力306MW的可逆式水泵水轮机。引水系统采用两洞四机竖井式布置(一洞两机),在竖井中部设置中平段。机组的设计参数为:水泵水轮机转轮高压侧进口直径2a=3 850.1 mm,低压侧出口直径4=1 934.8 mm,水轮机工况额定水头540m、额定流量62.09 m3/s、额定转速500 r/min,飞逸转速660 r/min,转轮叶片数9,活动导叶数20。调节保证要求:蜗壳进口中心线上最大压力(含压力脉动)不大于8.33 MPa,尾水管进口最小压力(含压力脉动)不小于0,输水道沿线洞顶最小内水压力不小于0.02 MPa,最大瞬态转速不大于1.5倍额定转速。
1.2 测试情况
2016年,洪屏电站机组启动调试过程中,每台机组分别进行了单机额定负荷试验,试验过程中测量了球阀前、蜗壳进口、尾水锥管、尾水出口等位置处压力,同时对导叶、球阀、出口断路器等动作情况进行了同步录波。单机甩负荷时,同一流道相邻机组为停机态,球阀关闭。四台机组单机甩额定负荷试验时的关键参数见表1所示。
本文重点对尾水锥管压力进行分析,压力传感器采用GE公司的PTX5072型传感器,精度为±0.2%,频响范围0~5 kHz(−3 dB);数据采集系统为HBM公司的QuantumX MX840A-P,模/数转换位数为24;数据采样率为1 200 Hz。
1.3 数据有效性评价
多数抽水蓄能机组尾水锥管埋置于混凝土中(仅锥管进人门处外露),通过布置长引水管路引至蜗壳层或水轮机层仪表盘测量尾水锥管处压力。此时,长测压管路引起管路水体共振效应将导致管路末端传感器安装位置处压力信号产生畸变,不能有效反应锥管内压力脉动情况[20]。而洪屏电站为检修方便,设计时尾水锥管设计成部分外露方式,安装了验水阀,具备现地测量条件。图1为安装于尾水锥管验水阀部位的压力传感器。

图1 尾水锥管压力测点
根据GB/T 17189-2017[18]和文献[20],该段测压管路的一阶特征频率1为:

式中a为水中声速,取1 450 m/s;L为管路长度,0.1 m。经计算,该段管路一阶特征频率为3 625 Hz。
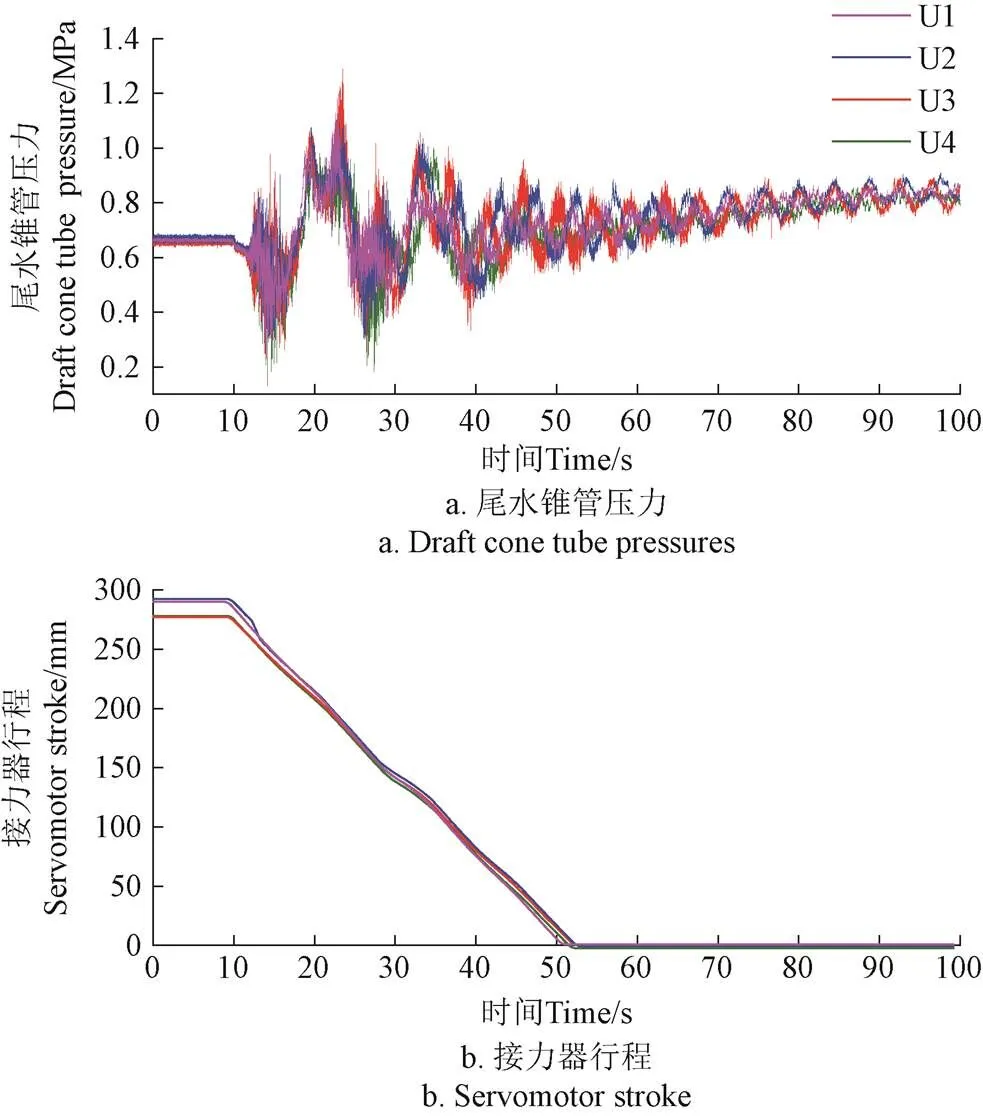
根据标准:“测量仪器应避免在0.11以上频率使用,并应采用低通滤波器”[18],压力信号的推荐采样频率应低于363Hz。甩负荷过程中,尾水锥管内以低频成分为主;不考虑卡门涡时,尾水锥管可能出现的高频成分为无叶区压力脉动所传递的叶片通过频率及其倍频。如采用363 Hz进行采样,考虑混叠效应后,信号有效频率成分低于142 Hz,不能实现叶片通过频率及其倍频的采样。故实际信号采样频率为1200Hz,此时能够有效分析尾水锥管压力信号中高频成分,但由于存在0.1 m长引水管路,非绝对就近测量,需要验证数据有效性,以判断压力信号中是否存在因管路共振导致的异常频率成分。四台机组甩额定负荷时尾水锥管压力见图2a所示,导叶动作情况见图2b所示。图2中将四台机组甩负荷时刻(发电机出口断路器动作时间)统一调整至相应数据段中的第10秒以便对比分析。
图2a可见:四台机组实测尾水锥管压力具有一致的变化规律;通过计算每两台机组尾水锥管实测压力相关系数表明,最小相关系数为0.66(3号与4号机组),最大相关系数为0.75(1号与4号机组),表现出明显相关性,进一步验证了四台机组甩额定负荷时尾水锥管压力具有一致的变化规律。图2b以接力器行程表示的导叶关闭规律基本重合,实测关闭速度数值见表1所示,关闭速度满足设计要求。
由于甩负荷过程为典型的非稳态过程,为此采用短时傅里叶变换对压力信号进行分析。图3为四台机组尾水锥管压力信号分析结果,取窗口长度1 s,步长0.1 s,采用汉宁窗函数进行加窗。图3中短时傅里叶变换结果图可见:甩负荷前,部分机组尾水锥管内主频为无叶区传递的动静干涉频率成分;甩负荷过程中,尾水锥管压力主要频率成分均为低频分量与动静干涉频率(18倍转频),低于测压管路一阶特征频率的0.1倍(0.11),且信号中无明显高频(300~600 Hz之间)混叠效应,数据有效。因此尾水锥管处测量条件满足GB/T17189-2017[18]以及IEC60041-1991[19]所要求的“宜采用传感器测头与流道内壁齐平方式安装传感器”,所测数据可以用于评估尾水锥管管壁处的压力及脉动情况。
注:U1~U4分别为1~4号机组。

图3 四台机组尾水锥管压力时频图
2 试验数据分析
2.1 压力趋势与脉动分析
当采用实测数据数值对一维数值模拟所得到的调节保证计算结果进行验证时,需要采用适当的技术手段获得实测信号中的压力趋势。压力趋势数据获取方法较多,如采用低通滤波器法[21]、经验模态分解法[22]、变分模态分解法[23]、Savitzky-Golay滤波器[24-26]等。经验模态分解与变分模态分解依赖参数较多,且存在模态混叠问题,Savitzky-Golay滤波器为线性滤波器,且算法较低通滤波器方法简单、易于实现,因此本文采用Savitzky-Golay滤波器对实测尾水锥管压力数据进行低通滤波处理,该滤波器为线性滤波器,低通截止频率f满足如下关系式[27]:
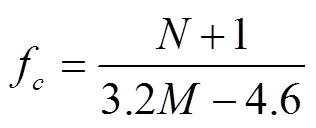
式中为滤波器阶数;为所用数据段长度的一半。
甩负荷过程中,锥管内存在空化,研究表明大尺度的空腔涡带引发的尾水管压力脉动主频均大于0.2倍转频[28-29],通常在0.2~0.5倍转频之间。一维数值模拟时通假定管道中水体不可压缩、断面内水力学参数无差异、不考虑空化等问题[1],不能预测尾水管中的低频涡带,因此在低频趋势提取时,可以设置低通截止频率为0.1~0.2倍转频,此时可以抑制由空化导致的较高频率成分。洪屏电站机组转频为f=8.33Hz,压力信号采样率为1 200 Hz,故Savitzky-Golay滤波器参数设定为=376,=2,计算得f=1.5Hz。
采用如上参数的Savitzky-Golay滤波器对四台机组甩额定负荷时尾水锥管压力数据进行低通滤波获取压力趋势,结果如图4a所示,为便于对比分析,图中给出了实测机组转速波形曲线;压力脉动分析结果如图4b所示(压力脉动为原始采样数据与压力趋势的差值)。
由图4a尾水锥管压力趋势可见,四台机组转速变化曲线基本重合,受水泵水轮机转轮固有的“S”特性[29-38]影响,转速曲线出现3次明显的峰值,最高转速为额定转速的133.2%;四台机组尾水锥管压力趋势项变化规律一致,数据表现出了良好的一致性;尾水锥管压力最小值发生在其第一波谷处,接近转速最高附近,此时锥管内流量下降最快;尾水锥管压力最大值发生在转速波谷阶段。
图4b中的尾水锥管压力脉动时域波形也基本具有基本一致的变化规律。锥管压力脉动所受影响因素较多,在甩负荷后,锥管内发生空化现象,形成空化涡带[3,31],造成压力脉动增大;同时,由于转速升高、流动受阻,转轮与导叶间的动静干涉现象增大[16],并向转轮出口传播(图3中可见明显的动静干涉频率成分);受水泵水轮机转轮“S”形特性影响,无叶区及转轮内将发生旋转失速现象[32],旋转失速也将对压力脉动产生一定影响。根据相关标准[18],稳态工况下的压力脉动采用峰峰值进行评价。对于稳态数据,当数据分析时长满足一定条件时,峰峰值大小与时长近似无关[33];暂态情况下,当时长较大时所获得的峰峰值不能准确反映压力脉动强度的变化规律,而当时长较小时所获得的峰峰值不稳定,因此图5给出了图4b所示压力脉动不同时长下的峰峰值,图5中峰峰值计算时采用的分位数分别为1.5%和98.5%[18]。
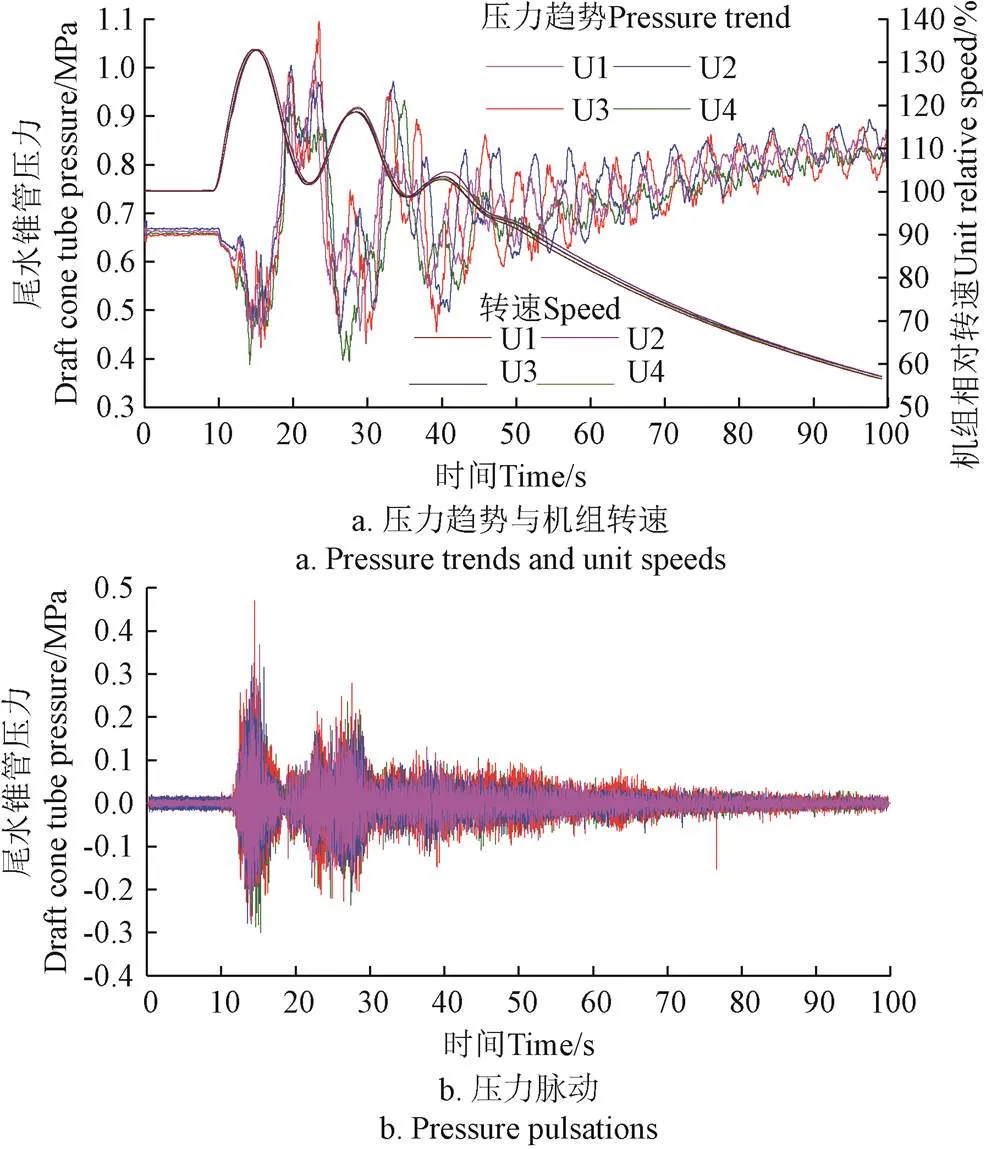
图4 四台机组尾水锥管压力趋势与脉动及机组转速
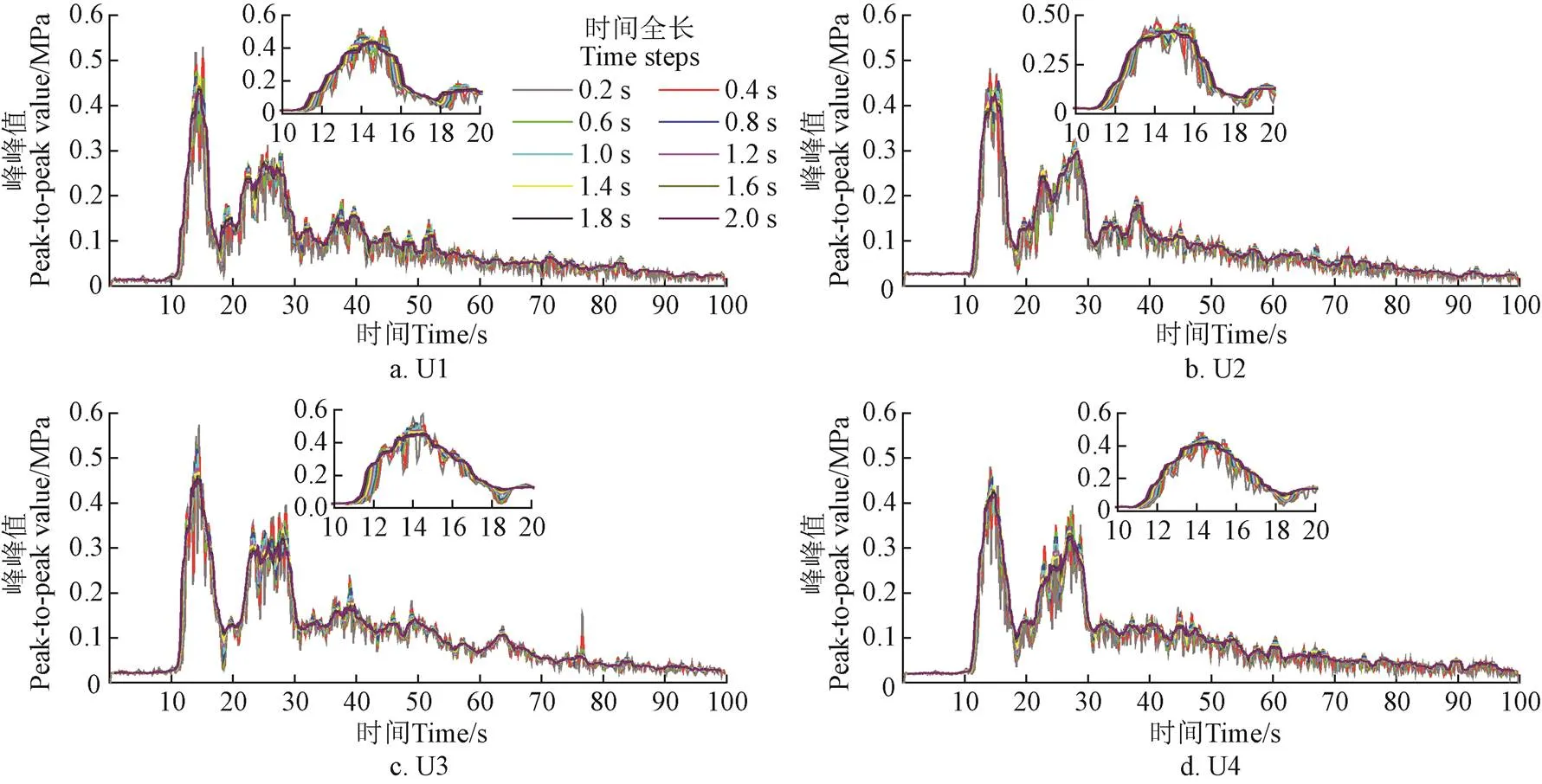
图5 不同时长下的四台机组尾水锥管压力脉动项峰峰值趋势
由图5可见:四台机组甩额定负荷时的压力脉动峰峰值趋势变化整体表现出一致的变化规律,存在2次明显的峰峰值增大过程,大致对应2次转速峰值时刻;对具体单台机组,脉动峰峰值的大小与计算时长有密切关系,但不同时长获得的峰峰值趋势一致;最大峰峰值方面,四台机组均在14.2 s时压力脉动峰峰值达到最大值。
2.2 调节保证值验证
根据标准[8-10],调节保证设计值是水力过渡过程计算值叠加压力脉动和计算误差修正获得。水力过渡过程计算值是一维数学模型压力计算曲线的极值,这种叠加仅发生在水力过渡过程计算的极值点上。对尾水锥管,调节保证设计值的最低值为:水力过渡过程计算值(极小值)减去压力脉动,再扣除计算误差修正。由于工程经验较少,标准[8-10]给出的压力脉动和计算误差均是范围值,工程设计时不同的取值给技术经济评价与分析带来了一定的不确定性。在工程竣工验收时,如何分析与评价实测尾水锥管压力数据也带来了一定困扰,这主要表现在如何根据实测数据校验标准中的压力脉动与计算误差。为此,针对实测尾水锥管压力,本文将其简化:考虑到大量的研究及工程实践均表明一维数学模型计算得到的水力过渡过程计算结果与实测信号的趋势项相符,可以认为实测尾水锥管压力中去除低频趋势后的脉动数据即为需要评估的压力脉动,该压力脉动对应标准中的压力脉动误差与水头误差修正,对其进行研究有助于反演分析其他工况,诸如依据当前水头甩负荷结果评估极端工况甩负荷情况等。此时需要考虑的问题等价为:对尾水锥管管壁压力测点而言,实测压力脉动最大峰峰值是多少;压力趋势项的极值点是否对应压力脉动的最大值。由于四台机组数据具有良好的一致性,为此,以图5中脉动峰峰值最大时刻14.2 s为中心,改变峰峰值计算所用数据时长,从而获得变时长情况下压力脉动最大峰峰值的变化趋势,结果见图6所示。
图6可知:以14.2 s为中心,随着时长增大,四台机组脉动峰峰值趋势一致,均存在最大脉动峰峰值,且脉动峰峰值先急速增大而后缓慢降低。初始阶段,由于时长短,所用数据量较少,峰峰值不能代表实际压力脉动特征,导致峰峰值偏小;时长增大到一定程度后,根据峰峰值算法,上、下分位数所对应的数值相对稳定,导致时长虽然增大,但峰峰值趋于稳定。经计算洪屏电站四台机组压力脉动数据,其最大峰峰值与时长分别为0.489 MPa与0.46 s、0.477 MPa与0.09 s、0.532 MPa与0.66 s和0.486 MPa与0.11 s,平均值为0.496 MPa与0.33 s,最大峰峰值分别为工作水头的8.94%、8.69%、9.59%和8.77%,平均为8.99%。受试验时的工作水头、尾水位、导叶关闭规律、某种程度上的压力脉动随机性以及测量误差等因素影响,最大压力脉动峰峰值和时长均存在不确定性,但四台机组最大峰峰值差异并不明显,计算所用的时长差别较大。
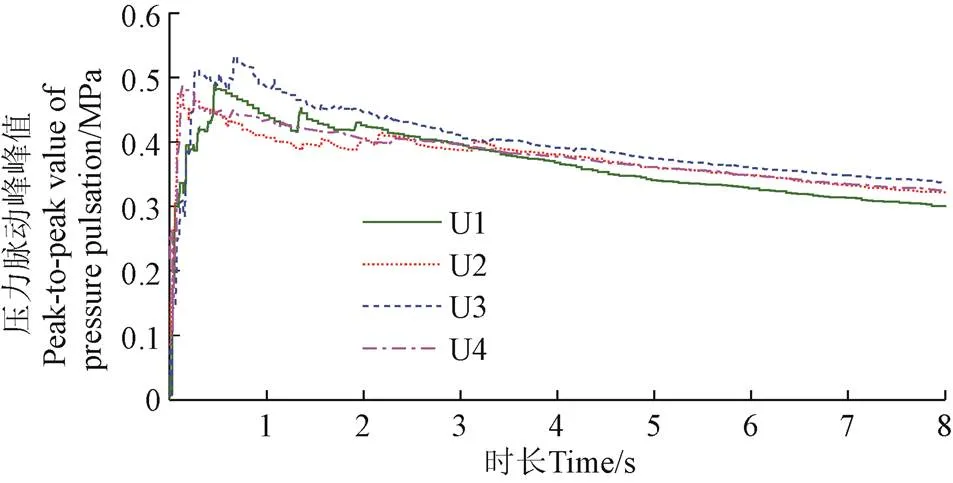
图6 四台机组压力脉动最大时峰峰值与时长关系
针对尾水锥管调节保证计算值修正是在一维数值模拟或压力趋势项最小值上进行,此时最小值点发生的时刻是否对应压力脉动最大值时刻是需要考虑的另一重要问题。由于抽水蓄能机组普遍没有监测实时流量的装置,原型机组甩负荷试验时流量不测,导致无法在全特性曲线上标识甩负荷后由单位转速11与单位流量11构成的轨迹线。但由于压力趋势项与一维数值模拟结果一致,因而可以用数值模拟的轨迹线近似实际甩负荷时的轨迹线。
图7基于SIMSEN 3.0.3平台建立的洪屏电站过渡过程计算模型,图8为通过该软件获得的四台机组甩额定负荷数值模拟结果,图9为相应甩负荷过程中由单位转速11和单位流量11所构成的轨迹线,以及尾水锥管压力脉动峰峰值最大值与压力趋势线最小值在轨迹线上的位置。
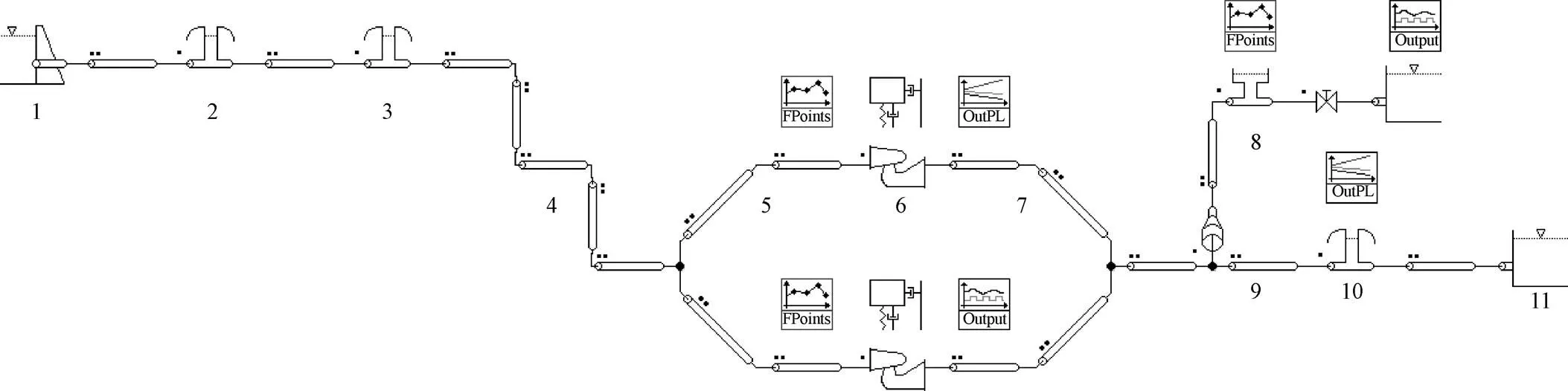
1.上库进水口 2.上游闸门井 3.上游调压室 4.上游引水总管 5.上游引水叉管 6.水泵水轮机 7.尾水支管 8.尾水调压井 9.尾水总管 10.下游闸门井 11.下库

图8 四台机组甩额定负荷尾水锥管压力数值模拟

图9 四台机组甩额定负荷时模拟轨迹线、尾水锥管压力最小模拟值与实测尾水锥管压力脉动最大值分布
由图8可见,四台机组甩额定负荷时,虽然水头和水位存在差异(表1所示),但是整体趋势基本重合;数值模拟曲线与图4a实测压力曲线趋势一致。
由图9可见,四台机组甩额定负荷后单位转速11与单位流量11轨迹线基本重合,表现出良好的一致性;甩负荷后,水泵水轮机进入S区内运行;压力脉动峰峰值最大值发生在轨迹线斜率由负转正时刻,位于飞逸线上侧;压力趋势极小值发生在S区内的反水泵工况零流量附近,处于轨迹线斜率由正转负时刻。
由图9分析可以得到:对洪屏抽水蓄能电站四台机组,甩额定负荷时尾水锥管压力脉动最大峰峰值时刻与数值模拟或压力趋势项最小值时刻之间存在偏差,即压力脉动峰峰值最大时刻并非趋势极小值发生的时刻。在此情况下,考虑到以最大峰峰值叠加至数值模拟最小值上相对而言偏保守,此时一种可行的方式为:采用平均值0.496 MPa/0.33 s对压力趋势和数值模拟极值进行修正。0.33 s对应2.74倍额定转速旋转周期,由于甩负荷后为变转速过程,且通常不采用准周期采样,其大致对应3~4个实际旋转周期。采用四台机组脉动峰峰值最大值的平均值重新复核得到表2结果。由于尾水锥管压力主要关注最小值,表2中给出了依据标准进行修订时的修正结果(3.5%工作水头的压力脉动与10%压力下降值的计算误差)。

表2 四台机组实测尾水锥管压力趋势、数值模拟极值与修正
分析表2数据可知:
1)针对测试数据趋势项采用四台机组压力脉动最大峰峰值的平均值修正时,U1、U2和U3修正后的锥管最小值小于实测值,U4锥管最小值略大于实测值(偏差0.009 MPa)。修正后的锥管最小值小于实测值,表明设计是偏保守的,将导致设计值有更大的裕量;对于U4而言,甩负荷时其与U3具有基本一致的水位条件、功率和关闭速度,但修正结果略小于实测值,其结果在可接受范围内。
2)针对测试数据趋势项采用四台机组压力脉动最大峰峰值的平均值修正时,修正后的锥管最大值均大于实测值,引起的原因是压力趋势项最大值时刻与压力脉动峰峰值最大值时刻并不一致,导致修正后误差增大,但这一修正对最大值而言是保守的,导致设计值有更大的裕量。
3)不考虑水头偏差修正,针对数值模拟的锥管压力最小值采用四台机组压力脉动最大峰峰值的平均值修正时,U1、U2和U3修正后锥管计算最小值小于实测最小值,而U4则大于略大于实测最小值(偏差0.025 MPa),相对水头和实测值而言,考虑压力传感器精度和测试系统误差,这一偏差仍是比较小的,在可接受范围内;对比依据标准修正后的锥管压力最小值可见,依据标准修正的U1、U2和U3锥管压力最小值小于实测数据,而U4则大于实测数据,而采用实测压力脉动最大峰峰值修正的结果更小,表明采用实测压力脉动最大值修订时裕量较大,采用标准推荐的最大值3.5%修正时更加接近实测值。
4)不考虑水头偏差修正,针对数值模拟的锥管压力最大值采用四台机组压力脉动最大峰峰值的平均值修正时,四台机组修正后锥管压力计算最大值均大于实测最大值,其主要原因是计算数据最大值时脉动压力峰峰值较小,导致修正后误差增大,但同样这一修正对最大值而言是保守的,将导致设计值有更大裕量。对比依据标准修正后的锥管压力最大值可见,采用实测压力脉动最大峰峰值修正的结果比依据标准修正的结果略大、裕量偏大。
针对尾水锥管实测压力趋势和数值模拟压力数据,通过实测四台机组尾水锥管压力脉动峰峰值最大值的平均值进行修正分析,可以得到:修正后的锥管压力最大值大于实测值,修正后的锥管压力最小值基本小于实测值。因而,对尾水锥管压力采用实测的压力脉动峰峰值最大值对数值模拟极值直接进行修正较标准规定的修正方法更保守,在调节保证验证时是可行的。
2.3 尾水锥管压力调节保证值修正流程
综合以上分析,针对洪屏抽水蓄能电站调节保证验证及校核过程中尾水锥管压力的修正,可以形成以下流程:
1)针对实测锥管压力数据采用低通滤波器(低通截止频率宜为0.1~0.2倍转频)获取压力趋势和压力脉动数据;
2)针对压力脉动数据采用3~4个旋转周期对应时长的数据计算峰峰值变化规律,可以获得压力脉动项最大峰峰值;
3)针对压力趋势或者一维数值模拟所获极值采用压力脉动最大峰峰值进行修正。
由于实测锥管边壁测点压力趋势项某一时刻值是该断面测量位置处径向最大值,断面压力的平均值小于该值,故采用本方法修正后的锥管压力最小值是避免甩负荷后发生水柱分离-弥合现象的合理保证。模型试验方面,虽然获得了锥管截面的压力分布情况,但由于模型与原型在锥管压力脉动方面不相似,原型机组与模型机组之间存在差异,且对原型机的锥管截面压力分布测量难度极大,尚未有相关报道,导致不能给出边壁压力与断面平均压力之间的关系(这点可以通过计算流体动力学实现,但仍缺乏验证)。一旦该问题能够突破,则可以给出避免甩负荷后发生水柱分离-弥合现象的合理保证。
3 结 论
本文对调节保证时尾水锥管压力最小值含义进行了多角度阐释,梳理了涉及尾水锥管压力的国内相关标准,在此基础上,针对洪屏抽水蓄能电站调试阶段四台机组甩负荷时的尾水锥管压力实测数据进行了详细分析,提出了具有指导意义的压力脉动修正方法,为得到安全、经济、合理的调节保证修正方法提供了有益参考,获得以下结论:
1)调节保证计算工况发生的锥管压力最小值是:甩负荷后的任意时刻任意锥管断面不发生水柱分离-弥合现象,由于甩负荷后尾水锥管内存在严重空化现象,该值非实际尾水锥管发生的最小值;
2)采用低通截止频率为0.1~0.2倍转频的滤波器对实测压力数据进行处理所获得压力趋势项,与一维过渡过程数值模拟结果一致,可以实现对一维过渡过程数值模拟有效性的验证,同时分离出压力脉动;压力脉动峰峰值存在极大值;采用压力脉动最大值对一维过渡过程数值模拟数据进行修正,可以获得避免甩负荷后发生水柱分离-弥合现象的压力值合理保证。
[1] Streeter V L, Wylie E B. Fluid Transients in Systems[M]. Upper Saddle River: Prentice-Hall, 1993.
[2] 付亮,鲍海艳,田海平,等. 基于实测甩负荷的水轮机力矩特性曲线拟合[J]. 农业工程学报,2018,34(19):66-73.
Fu Liang, Bao Haiyan, Tian Haiping, et al. Fitting of hydro turbine torque characteristic curves based on load rejection test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(19): 66-73. (in Chinese with English abstract)
[3] Nonoshita T, Matsumoto Y, Ohashi H, et al. Water column separation in a straight draft tube[C]//. 3rdASME/JSME Joint Fluids Engineering Conference, San Francisco, 1999.
[4] Kiani A, Brekke H, Leyland B, et al. Transient problems upon load rejection Masjed-e Soleyman case study[C]// Hydro 2004, Portugal, 2004.
[5] Pejovic S, Zhang Q F, Karney B, et al. Analysis of pump-turbine ‘S’ instability and reverse water hammer incidents in hydropower systems[C]// Fourth International Meeting on Cavitation and Dynamic Problems in Hydraulic Machinery Systems, Belgrade, 2011.
[6] Pejovic S, Karney B, Zhang Q F. Water column separation in long tailrace tunnel[C]// Hydroturbo 2004 on Hydro-power Engineering International Conference, Brno, 2004.
[7] 水电水利规划设计总院.水电规机电[2013]12号关于印发水电站输水发电系统调节保证设计专题报告编制暂行规定(试行)的通知[Z]. 2013.
[8] 中国电力企业联合会. T/CEC 5010-2019 抽水蓄能电站水力过渡过程计算分析导则[S]. 北京:中国电力出版社,2019.
[9] 国家能源局. NB/T 10072-2018 抽水蓄能电站设计规范[S].北京:中国电力出版社,2019.
[10] 中华人民共和国国家发展和改革委员会. DL/T 5186-2004 水力发电厂机电设计规范[S]. 北京:中国电力出版社,2004.
[11] 孙龙刚,郭鹏程,罗兴锜. 基于不同涡识别准则的水轮机尾水管涡带形态识别研究[J]. 水动力学研究与进展,2019,34(6):779-787.
Sun Longgang, Guo Pengcheng, Luo Xingqi. Visualization investigation into precessing vortex in Francis turbine draft tube based on several vortex identification criterions[J]. Chinese Journal of Hydrodynamics, 2019, 34(6): 779-787. (in Chinese with English abstract)
[12] Tsujimoto, Y. Cavitation instabilities in hydraulic machines[C]// IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2013.
[13] 莫伦科夫 G,拉贝 J. 混流式水轮机尾水管内脉动速度和脉动压力的测量[M]//中国科学院水利电力部水利水电科学研究院. 水轮机水力振动译文集. 北京:水力电力出版社,1979.
[14] 常近时. 宇宙射线电离强度对清水空化压力特性的决定性影响[J]. 中国科学E辑:技术科学,2008,38(11):1970-1975.
Chang Jinshi. The decisive influence of cosmic ray ionization intensity on the cavitation pressure characteristics of water[J]. Science China Series E: Technical Science, 2008, 38(11): 1970-1975. (in Chinese with English abstract)
[15] Liu Jintao, Liu Shuhong, Sun Yuekun, et al. Three dimensional flow simulation of load rejection of a prototype pump-turbine[J]. Engineering with Computers, 2013, 29(4): 417-426.
[16] 周勤,夏林生,张春泽,等. 水泵水轮机甩负荷过程中的压力脉动和转轮受力[J]. 水利学报,2018,49(11):1429-1438.
Zhou Qin, Xia Linsheng, Zhang Chunze, et al. Transient pressure fluctuations and runner loadings of a model pump-turbine during a load rejection process[J]. Journal of Hydraulic Engineering, 2018, 49(11): 1429-1438. (in Chinese with English abstract)
[17] 毛秀丽,孙奥冉,Giorgio P,等. 水泵水轮机甩负荷过程流动诱导噪声数值模拟[J]. 农业工程学报,2018,34(20):52-58.
Mao Xiuli, Sun Aoran, Giorgio P, et al. Simulation of flow induced noise in process of pump-turbine load rejection[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(20): 52-58. (in Chinese with English abstract)
[18] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. GB/T 17189-2017 水力机械(水轮机、蓄能泵和水泵水轮机)振动和脉动现场测试规程. 北京:中国标准出版社,2018.
[19] International Electrotechnical Commission. IEC60041-1991 Field acceptance tests to determine the hydraulic performance of hydraulic turbines, storage pumps and pump-turbines. Geneva: International Electrotechnical Commission, 1991.
[20] 张飞,郭磊,宫让勤,等. 基于线性摩擦模型的水力机械测压管路特性[J]. 工程热物理学报,2018,39(8):1725-1730.
Zhang Fei, Guo Lei, Gong Rangqin, et al. Pressure measurement pipe characteristics of hydraulic machinery based on linear friction model[J]. Journal of Engineering Thermophysics, 2018, 39(8): 1725-1730. (in Chinese with English abstract)
[21] 付亮,黄波,邹桂丽,等. 基于真机实测的双机共尾水调压室水电站同甩负荷仿真[J]. 水利水电技术,2018,49(11):116-122.
Fu Liang, Huang Bo, Zou Guili, et al. Real-machine testing-based simulation on double units load shedding of hydropower station with tailrace surge chamber shared by two units[J]. Water Resources and Hydropower Engineering, 2018, 49(11): 116-122. (in Chinese with English abstract)
[22] 张飞,宫让勤,秦俊,等. 基于经验模态分解的蓄能机组甩负荷压力数据处理[J]. 水电能源科学,2017,35(6):132-135.
Zhang Fei, Gong Rangqin, Qin Jun, et al. Pressure data processing in load rejection test of pumped-storage unit based on empirical mode decomposition[J]. Water Resources and Power, 2017, 35(6): 132-135. (in Chinese with English abstract)
[23] 曹林宁,蒋磊,陈忠宾,等. 基于VMD的甩负荷试验尾水管压力分析及预测[J]. 中国农村水利水电,2020,62(2):148-152.
Cao Linning, Jiang Lei, Chen Zhongbin, et al. Analysis and prediction of water pressure of the draft tube in load rejection test based on VMD[J]. China Rural Water and Hydropower, 2020, 62(2): 148-152. (in Chinese with English abstract)
[24] 杨建东,胡金弘,曾威,等. 原型混流式水泵水轮机过渡过程中的压力脉动[J]. 水利学报,2016,47(7):858-864.
Yang Jiandong, Hu Jinhong, Zeng Wei, et al. Transient pressure pulsations of prototype Francis pump-turbines[J]. Journal of Hydraulic Engineering, 2016, 47(7): 858-864. (in Chinese with English abstract)
[25] Chirag T, Michel C, Bhupendra G, et al. Transient pressure measurements on a high head model Francis turbine during emergency Shutdown, total load rejection, and runaway[J]. ASME Journal of Fluids Engineering, 2014, 136(12): 121107
[26] Chirag T, Michel C, Bhupendra G, et al. Pressure measurements on a high-head Francis turbine during load acceptance and rejection[J]. Journal of Hydraulic Research, 2014, 52(1): 1-15.
[27] Schafer R W. What is a Savitzky-Golay filter?[J]. IEEE Signal Processing Magazine, 2011, 28(4): 111-117.
[28] 李琪飞,赵超本,龙世灿,等. 水泵水轮机飞逸工况下尾水管涡带演化研究[J]. 振动与冲击,2019,38(4):222-228.
Li Qifei, Zhao Chaoben, Long Shican, et al. A study on evolution of vortex in the draft tube of pump-turbine under the runaway condition[J]. Journal of Vibration and Shock. 2019, 38(4): 222-228. (in Chinese with English abstract)
[29] Michihiro N, Liu S H. An outlook on the draft-tube-surge study[J]. International Journal of Fluid Machinery and Systems, 2013, 6(1): 33-48.
[30] Zhang Y, Zhang Y, Wu Y. A review of rotating stall in reversible pump turbine[J]. Journal of Mechanical Engineering Science, 2017, 231(7): 1181-1204.
[31] Tsujimoto Y. Cavitation instabilities in hydraulic machines[C]//. 6th International Conference on Pumps and Fans with Compressors and Wind Turbines, 2013, 52(1): 012005
[32] Wang Leqin, Yin Junlian, Jiao Lei, et al. Numerical investigation on the “S” characteristics of a reduced pump turbine model[J]. Sci China Tech Sci, 2011, 54(5): 1259-1266.
[33] 张飞,葛新峰,潘罗平,等. 稳态工况下水电机组主轴摆度峰峰值计算方法研究[J]. 振动与冲击,2015,34(21):170-174.
Zhang Fei, Ge Xinfeng, Pan Luoping, et al. Shaft runout’s peak-to-peak value calculation method for a hydraulic power unit under stable conditions[J]. Journal of Vibration and Shock, 2015, 34(21): 170-174. (in Chinese with English abstract)
Draft cone tube pressure of pumped-storage power unit in load rejection test
Zhang Fei1, Wang Xianping2
(1.100053,;.,200240,)
One of the key control parameters in hydraulic transient process of pumped-storage power unit is draft cone tube pressure, which should be within the design value. The design value is calculated by one dimension mathematical model of hydraulic transient theory with considering on certain pressure pulsation correction and calculation error. For a long time, there is non-negligible deviation between the calculated value by one dimension numerical simulation and the measured value of draft cone tube from on-site load rejection test. Henceforth, once engineers use measured values to check calculation results, they can not get reasonable explanation and evaluation between simulation results and measured values. In order to settle the difference between regulation guarantee calculation value and measured value, minimum pressure of draft cone tube was clarified from multiple perspectives in this paper, and Chinese standards or codes relating to hydraulic transient calculation were reviewed. The standard research indicates that for pumped storage unit, the minimum draft cone tube pressure should not below -0.08MPa in any circumstances. Measured draft cone tube pressure data of the rated load rejection tests performed in Hongping pumped storage power station during commissioning period was investigated. Firstly, field measuring conditions of draft cone tube pressure was thoroughly assessed and confirmed, and the validity of measured pressure was verified by using short-time-Fourier-transform to analyse the frequency characteristics. The frequencies of four draft cone tube pressure are similar, of which are low frequency component and rotor-stator frequency. The main frequencies are lower than first order eigen frequency of measuring pipes. The obtained data can be regarded as near wall measured pressure. Secondly, Savitzky-Golay filter was employed to separate trend and pulsation of measured draft cone tube pressure. The separated pressure trend can be deemed as the average section pressure of draft cone tube in one dimension numerical simulation, and the pressure pulsation represents the fluid complexity in the hydraulic transients. For pressure pulsations, relationship between maximum peak-to-peak values and time lengths were studied. For Hongping pumped-storage units, the maximum peak-to-peak values and time lengths of each unit are 0.489 MPa/0.46 s, 0.477 MPa/0.09 s, 0.532 MPa/0.66 s and 0.486 MPa/0.11 s, the average is 0.496 MPa/0.33 s. Consistency between pressure trends and one-dimension simulation results was verified. The verfication indicates that the guide vane closing principles are the same and pressure trends comply with the simulation results well. Thirdly, maximum peak-to-peak value of pressure pulsation was used to correct the one-dimension simulation results and trend items. The correction of draft cone tube has negligible errors with on-site measured values. Finally, the correction process was summarized for the hydraulic transient calculation of draft cone tube. The case study indicates that the pressure trend, which is consistent with one-dimension simulation result, can be effectively separated from measured draft cone tube pressure by using low-pass filter with cutoff frequency of 0.1-0.2 times rated rotational frequency; the maximum peak-to-peak value of pressure pulsation can be obtained by selecting data of 3-4 rotational periods; hydraulic transient calculation of draft cone tube can be effectively corrected and verified by superposing the maximum peak-to-peak value of measured pressure pulsation. The research provides effective support for regulation guarantee design and verification of pumped-storage power units.
pressure pulsation; numerical simulation; regulation guarantee calculation; draft cone tube pressure; Savitzky-Golay filter
张飞,王宪平. 抽水蓄能机组甩负荷试验时尾水锥管压力[J]. 农业工程学报,2020,36(20):93-101.doi:10.11975/j.issn.1002-6819.2020.20.012 http://www.tcsae.org
Zhang Fei, Wang Xianping. Draft cone tube pressure of pumped-storage power unit in load rejection test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(20): 93-101. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2020.20.012 http://www.tcsae.org
2020-06-30
2020-10-12
国家电网公司科技项目(52573020000B);国家自然科学基金资助项目(51809082);中国水科院基本科研业务费项目(HM0145B242020)
张飞,高级工程师,从事抽水蓄能机组性能测试技术研究与服务工作。Email:spiritgiant@126.com
10.11975/j.issn.1002-6819.2020.20.012
TK734
A
1002-6819(2020)-20-0093-09

