欧式距离与标准化欧式距离在k近邻算法中的比较

丁义 杨建

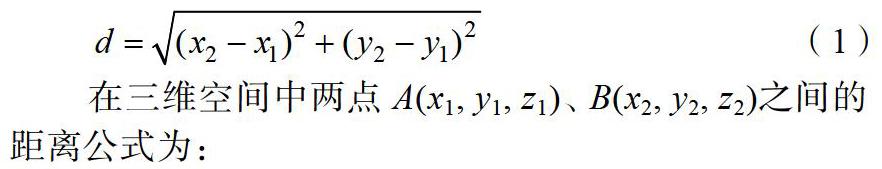
摘  要： 相似性度量是综合评定两个数据样本之间差异的指标，欧式距离是较为常用的相似性度量方法之一。本文分析了欧式距离与标准化的欧式距离在KNN算法中对数据分类的影响。仿真实验结果表明，当向量之间的各维度的尺度差别较大时，标准化的欧式距离较好地改善了分类的性能。

关键词： 欧式距离;标准化欧式距离;K近邻算法

中图分类号： TP311    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2020.10.033

本文著录格式：丁义，杨建. 欧式距离与标准化欧式距离在k近邻算法中的比较[J]. 软件，2020，41（10）：135136+140

【Abstract】： Similarity measurement is an index to evaluate the difference between two data samples. Euclidean distance is one of the most common similarity measurement methods. This paper analyzes the influence of Euclidean distance and standardized Euclidean distance on data classification in KNN algorithm. The simulation results show that the normalized Euclidean distance improves the classification performance as the scales of the dimensions between vectors differ greatly.

【Key words】： Euclidean distance; Standardized Euclidean distance; K-nearest neighbor algorithm

0  引言

K近邻（k-Nearest Neighbor，KNN）算法[1]，是一种理论上比较成熟的方法，也是最简单的机器学习算法之一，获得了广泛的实际应用[2-5]。KNN算法的基本思想是，在特征空间中，如果一个样本附近的k个最邻近样本的大多数属于某一个类别，则该样本也属于这个类别。即给定一个训练数据集，对新的输入样本，在训练数据集中找到与该样本最邻近的k个样本如果这k个样本中大多数属于某一个类别，就把该输入样本分类到这个类别中。目前，KNN在分类算法中获得了广泛的应用。KNN是一种基于实例的学习算法，它不同于决策树、贝叶斯网络等算法。决策树算法是一种逼近离散函数值的方法，它首先对待分类的数据进行预处理，之后用归纳算法生成规则和决策树。贝叶斯网络又称为置信网络或信念网络，它是基于有向无环图来刻画属性之间的依赖关系的一种网络结构，使用条件概率表来描述变量的联合概率分布。在KNN中，当有新的实例出现时，直接在训练数据集中找k个最近的实例，并把这个新的实例分配给这k个训练实例中实例数最多的类，它不需要训练过程，在类的边界比较清晰的情况下分类的准确率较好。KNN算法需要人为决定k的取值，即找几个最近的实例，k值不同，分类结果的结果也会不同。

相似性度量是综合评定两个样本之间相近程度的一种度量，两个样本越接近，它们之间的相似性度量也就越大;反之，两个样本差别越大，它们的相似性度量也就越小。一般情况下，采用距离度量两个样本的相似程度，数值越小，距离越近，而相似度越大;而距离越大，相似程度也越远。相似性度量应用广泛，例如测度两幅图像相似程度的图像相似性度量，在图像检索中获得了广泛应用;在购物网站中，确定两个用户或商品的向量之间的相似程度，以根据用户喜好向用户推荐商品。在KNN算法中，距离相似性度量的种类有多种，一般根据实际问题进行选用。

本文基于两种常用的距离，即欧式距离和标准化欧式距离，在给定数据集各向量之间的维度尺度差别较大时，来对它们在KNN算法中得到的效果进行比较。

1  欧式距离与标准化欧式距离

欧氏距离是最简单和易于理解的一种距离计算方法，来源于欧几里得几何中两点间的距离公式。设在二维平面上的两个点分别为A（x1，y1）、B（x2，y2），则A、B两点间的欧式距离为：

欧式距离尽管应用较为普遍，但它适用于样本向量的各个分量度量标准统一的情形。对绝大部分统计问题来说，由于样本分量的取值对欧氏距离的贡献是相同的，往往不能取得令人满意的效果。特别是当各分量的波动范围量纲差距较大时，会引起各分量对总体的贡献差别较大，甚至某一坐标的贡献几乎可以忽略不计，当各个分量为不同性质的量时，欧式距离的大小與样本分量的单位有关。例如某维向量的取值范围为[0，1]，而另一维向量的取值范围为[0，100]，前者变量的波动范围对距离计算的影响很小，甚至可以忽略不计。在这种情况下，合理的方法应该是对各个坐标分量加权，使变化较大的坐标比变化较小的坐标有较小的权重系数，将样本的不同属性之间的差异量化到同一个区间。在某些特殊应用时，也可以对样本分量的不同属性分别赋予不同的权重，从而取得更理想的计算效果。

标准化欧氏距离是针对简单欧氏距离的缺点而提出的一种改进方案，当向量之间的各维度的尺度差别较大时，使用简单欧氏距离使得各向量对最终分类结果产生较大的影响。标准化欧氏距离的思想是，将数据各维分量的分布进行归一化处理，将数据的各个分量均标准化到均值、方差。假设样本集S的均值为m，标准差为sd，则将特征S标准化为均值为零方差为1的变量。因此，两个归一化后的n维向量A（x1， x2， …， xn）、B（y1， y2， …， yn）间的标准化欧氏距离可以表示为：

2  KNN算法

K近邻算法是数据挖掘分类技术中最常用的方法，它的算法流程如下：

（1）分析数据，对数据预处理。删除含有缺失值的特征，采用PCA[6，7]对数据集进行特征选择降维处理。

（2）导入数据集。

（3）设置参数k。因为进行分类的策略是按照多数类来划分，所以一般k选择奇数。

（4）分别采用公式（3）和（5）两种方法计算特征之间的距离。

（5）判定属于哪一类别，应用计算出的分类执行后续处理。算法流程如图1所示。

标准化的欧式距离相当于对样本产生的影响赋予不同的权重[8]。当样本不平衡时，如一个类的样本容量很大，而其它类样本容量较小时，当输入一个新样本时，可能导致该样本的k个近邻中大容量类的样本占多数，而那些容量较小的样本采用这种算法比较容易产生错误分类。KNN算法不仅可以用于分类，也可用于回归，根据现有数据对数据分类边界建立回归公式，从而找到最佳拟合参数。利用逻辑回归进行分类的主要思想是，根据已知的数据对分类边界建立回归公式，并以此进行分类。KNN算法的优点是精度高，对输入数据的异常值不敏感，无数据输入假定，对数值型数据和标称型数据都能适用;不足之处是运算量较大，计算复杂度和空间复杂度相对较高，同时占用较多的存储资源，因为对每一个待分类的样本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。

3  实验结果

图2和图3分别给出了两种方法在数据集上的分类效果。k值的选择会影响算法的结果，k值较大时，可以减少训练中的误差估计，但缺点是与输入样本距离较远的训练样本也会对预测起作用，使预测差错率提高，k值较小意味着只有与输入样本距离较近的训练样本才会对预测结果发生作用，容易发生过拟合。实验中选择k的值为3。从图中可以看出，采用标准化的欧式距离，分类边界效果更清晰，分类效果更有效。为了测试数据的分类效果，可以使用带标签的数据，检验分类器给出的结果是否与给定的标签一致，通过大量的测试数据，可以计算出分类器的错误率，即分类错误的样本数与样本总数之比。在分类执行过程中，算法必须保留全部数据，如果训练数据集很大，则会占用较多的存储空间。由于必须对数据集中的每个数据都需要计算距离值，对较大的数据集来说，算法需要较长的运行时间。

4  结论

本文基于在实际数据分类中获得广泛应用的k近邻算法，分析了欧式距离和标准化欧式距离对算法的影响，对绝大部分统计问题来说，由于样本分量的取值对欧氏距离的贡献相同，往往不能取得令人满意的效果。标准化欧氏距离是针对简单欧氏距离的缺点而提出的一种改进方案，当样本的各个特征属性的取值范围差别较大时，使用简单欧氏距离使得各向量对最终分类结果产生较大的影响，从而使得最终分类效果不理想。采用标准化的欧式距离，克服了数据特征的取值范围波动的差异，能夠优化数据之间的离散程度，使样本的各个特征之间量纲统一，也可以根据具体实际应用，赋予不同特征之间不同的权重，从而取得较好的分类效果。

参考文献

[1]T. Cover， P. Hart. Nearest neighbor pattern classification. IEEE Transactions on Information Theory. 1967.

[2]Pal， Nikhil R.， Ghosh， Swati. Some classification algorithms integrating Dempster-Shafer theory of evidence with the rank nearest neighbor rules. IEEE Transactions on Systems， Man， and Cybernetics Part A：Systems and Humans. 2001.

[3]Yigit H. A weighting approach for KNN classifier. 2013 International Conference on （ICECCO）Electronics， Computer and Computation. 2013.

[4]Weiss S M， Indurkhya N. Rule-based regression. IJCAI Proceedings of the International Joint Conference on Artificial Intelligence. 1993.

[5]Meesad， P， Hengpraprohm， K. Combination of KNN-Based Feature Selection and KNN Based Missing-Value Imputation of Microarray Data. 3rd International Conference on Innovative Computing Information and Control. 2008.

[6]Xiaojun Chang， Feiping Nie， Yi Yang， Chengqi Zhang， Heng Huang. Convex Sparse PCA for Unsupervised Feature Learning[J]. ACM Transactions on Knowledge Discovery from Data （TKDD）. 2016（1）.

[7]Reiff P A， Niziolek M M. RN. Troubleshooting tips for PCA.[J]. 2001（4）.

[8]Mostafa A. Salama， Ghada Hassan. A Novel Feature Selection Measure Partnership-Gain[J]. International Journal of Online and Biomedical Engineering. 2019（4）.