基于数学形态学的螺纹轮廓曲线滤波方法

倪高烽 程维明

摘  要： 接触式螺纹测量系统采集到的表面原始螺纹轮廓信号中往往伴随着随机噪声，这对后续计算螺纹参数值的影响非常大，所以找到一种既能有效滤除噪声同时保护螺纹轮廓边缘而且在选取滤波参数上也比较方便的方法十分重要，本文将数学形态学运用到螺纹轮廓信号的滤波中，确定合适的结构元素及长度，以得到该方法的最优滤波效果。然后对螺纹仿真信号进行试验，以均方根误差和信噪比作为滤波效果的评价指标。最后用实测螺纹轮廓信号进行检验，结果表明，形态学滤波方法能有效逼近期望螺纹轮廓信号，同时滤波参数的选取简单适应范围广。

关键词： 数学形态学;螺纹测量;滤波方法

中图分类号： TP3    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2020.10.018

本文著录格式：倪高烽，程维明. 基于数学形态学的螺纹轮廓曲线滤波方法[J]. 软件，2020，41（10）：7680

【Abstract】： The original thread profile signal of the surface collected by the contact thread measurement system is often accompanied by random noise， which has a great influence on the subsequent calculation of the thread parameter value. It is also very important that the filtering parameters are more convenient. In this paper， mathematical morphology is applied to the filtering of thread profile signals to determine the appropriate structural elements and lengths to obtain the optimal filtering effect of the method. Then the thread simulation signal is tested， and the root-mean-square error and signal-to-noise ratio are used as the evaluation indexes of the filtering effect. Finally， the actual measured thread contour signal is used for testing. The results show that the morphological filtering method can effectively approximate the expected thread contour signal， and the selection of filtering parameters is simple and has a wide range of adaptation.

【Key words】： P Mathematical morphology; Thread measurement; Filtering method

0  引言

接触式螺纹测量系统采集到的点云数据由于测量误差、测量环境噪声以及螺纹表面质量等因素的存在，如果直接利用这些数据进行数据拟合和参数计算必然会出现较大的误差，所以需要先进行信号数据的滤波处理。

对于螺纹轮廓信号的滤波，在滤除噪声并保护牙形轮廓边缘的同时，还要保证滤波参数选取简便，实现起来方便高效。传统的螺纹轮廓信号滤波方法如平滑滤波，能有效抑制小幅高频噪声[1]，但是该方法滤波前后存在相位偏移，也会平滑掉螺纹边缘特征，同时滤波效果也受滤波窗口大小影响。在国际标准ISO11562中规定了高斯滤波器作为一种零相移滤波方法[2]能有效滤除表面噪声。然而高斯滤波器存在边缘效应的问题[3]，边缘效应会破坏螺纹轮廓信号牙形边缘特征，而且实际使用中该方法与高斯核的选取以及滤波窗口大小有很大关系。中值滤波去噪方法是一种非线性平滑去噪技术，它能够有效抑制噪声。而且中值滤波器不会增加新的数据，所以能保证数据分析的准确性[4]，但它滤波效果的好坏与窗口大小有很大关系，缺乏自适应性不适合螺纹轮廓信号的去噪。基于小波变换的滤波，因其具有低熵性，多分辨率性，可以很好地刻画信号非平稳特性等优点而被越来越多的使用[5-6]，但是小波滤波的结果和小波基、阈值函数以及分解层数有很大关系，在螺纹轮廓信号滤波中也缺乏自适应性。

鉴于上述各种传统滤波方法在螺纹轮廓信号滤波上的局限性，本文将数学形态学方法运用到螺纹轮廓信号的滤波中。数学形态学[7]从集合的角度分析和刻画信号，其基本思想是设计一个类似“探针”的结构元素[8]，通过该探针在信号中移动，对信号进行匹配计算， 达到提取信号、保持细节和抑制噪声的目的。因其在信号的分析处理过程中完全是在时域中进行的，所以信号时域的局部特征决定了处理效果的好坏，具有相移不衰減及幅值不偏移的优点，且该方法的基本运算只包含加减、取最大最小值，不涉及其它的复杂运算，算法简单[9]。

1  方法研究

1.1  螺纹轮廓信号数据

在使用实际测得的螺纹点云数据进行滤波处理时，因无法事先知道其真值，所以滤波效果评价起来比较困难，所以本文拟先采用模拟的一般梯形螺纹轮廓进行仿真处理，通过加入相应大小信噪比的高斯白噪声来模拟实际测得的螺纹点云数据，将已知模拟螺纹真值与滤波后的结果进行比较，定量地对滤波效果进行评价，最后用实际测得的某螺纹轮廓信号验证该方法效果。如图1所示为模拟的梯形螺纹及其某牙局部图，其牙形角为30°，引入50db高斯白噪声，一个牙形周期采样点为128个，其中牙顶牙底各46个点，左右牙侧各18个点。

1.2  数学形态学变换

数学形态学在一维信号处理中主要包括形态腐蚀、形态膨胀、形态开及形态闭四种基本算子。设输入信号，结构元素 其中N≥M，腐蚀和膨胀运算分别为：

对于式（1）腐蚀运算表达式以下列一维信号为例，其中结构元素中带圈○的元素，表示该结构元素的原点位置，元素字符*表示平移后信号无穷大的点。根据结构元素中每点位置，将信号右移X个点（如表示向右平移–1个点位），然后将平移后信号中的每个数值减去结构元素中该点位置上的数值，最后对所得的所有这些信号纵向逐点比较取最小值，便可以得到腐蚀结果。

根据式（2）膨胀表达式， 例中符号#表示平移后信号无穷小的点，对结构元素中的每一点位置将信号向左平移X个点，然后将平移后信号中的每个数值加上结构元素中该点位置上的数值，最后对所有这些信号纵向逐点比较取最大值，就可以得到膨胀运算结果。

腐蚀和膨胀都是不可逆运算，所以对腐蚀和膨胀进行不同的排列组合就可以得到不同的形态学变换即形态开与形态闭如：

数学形态学的开运算可以滤除信号上边缘的孤立点和毛刺，并削去尖峰。数学形态学的闭运算则可以滤除信号下边缘的孤立点和毛刺，并填补裂缝[10]。P.Maragos[11]为同时抑制正负脉冲噪声，将开运算和闭运算进行串联组合，构建了形态开—闭滤波器（OC）和形态闭—开滤波器（CO）：

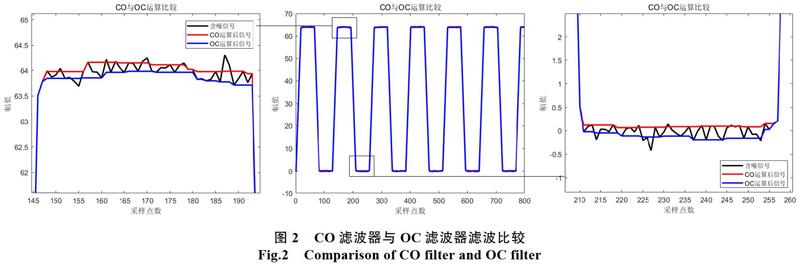
如图2所示，这两种滤波器都能有效滤除某螺纹信号中的噪声，但是由于开运算的收缩性和闭运算的扩张性，会导致开闭滤波器的输出偏小，闭开滤波器的输出偏大，从而存在统计偏移现象[12]。所以在螺纹轮廓信号滤波应用中，可以采用式7将上述两种滤波器取平均的方法来消除统计偏移的影响。

1.3  结构元素

形态滤波的效果和选取的结构元素有关，常用的结构元素有三角型、半圆型、扁平型等，结构元素g（n）的作用类似于对信号进行滤波处理时的“窗函数”，它的形状、宽度和高度这3个参数决定了输入信号中实际被保留的成分。一般只有与结构元素尺寸和形状相匹配的信号才能被有效保留[13]。因此需要采用与信号特征相匹配的结构元素才能实现较好的滤波效果，因为本文的主要研究目的是去除原始螺纹轮廓点云信号里的误差噪声，使得滤波后的螺纹轮廓尽可能平滑且棱角分明，所以在本研究中选用扁平结构元素，另一方面扁平型结构元素只有长度参数，具有计算简单、需要优化的参数少等优点。

1.4  结构元素长度选取

结构元素长度的选取十分重要，它决定了数学形态学滤波过程中信号每个采样点的滤波范围，结构元素长度过短就无法有效去除噪声成分，而过长容易导致有效信息过滤掉。国内外学者对结构元素长度选取进行了深入的研究。Dong[14]通过分别对不同长度结构元素处理信号后计算计算出的信噪比来选取最优结构元素长度，但是实际滤波时不知道原始波形数据，无法准确求得信噪比。Zhang[15]通过确定“局部峰值”来找到最佳的结构元素长度和高度。姜万录[16]通过计算滤波后的信号功率谱熵以及特征能量比来得出结构元素的最优长度尺寸。但这两种方法只適合噪声波动大的振动信号滤波或轴承故障的特征提取，并不适用于螺纹这样的信号。

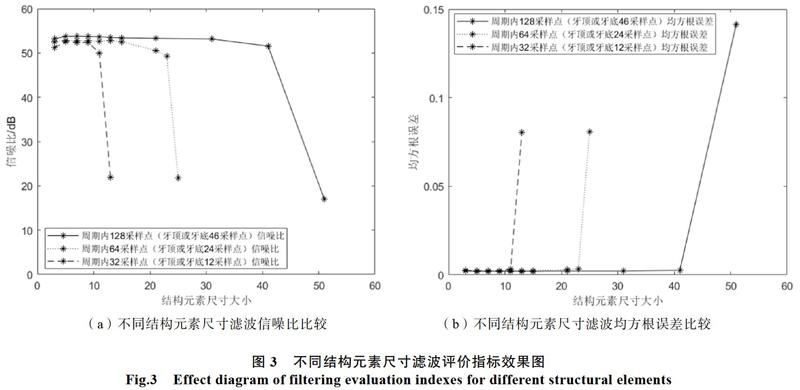
所以接下来研究形态滤波器结构元素长度对螺纹信号降噪性能的影响，考虑到不同螺纹轮廓一个牙形周期采样点数量的影响，对所模拟的螺纹轮廓信号分别进行隔一点和两点抽取，使一个牙形周期采样点分别为64点（牙顶牙底采样点数24）和32点（牙顶牙底采样点数12）。为确保计算结果不产生偏移，这里结构元素尺寸的点数选为奇数，用滤波前后的信噪比以及均方根误差来评价降噪性能，结果如图3所示。

从上图中可以发现结构元素尺寸的选择，与螺纹轮廓一牙形周期内牙顶或牙底处采样点数有关，结构元素尺寸超过牙顶或牙底处采样点数则会破坏螺纹信号;采样点数越多，该滤波方法效果也越好;牙顶或牙底处采样点数较大时，一般有多个较优的结构元素尺寸使滤波效果比较相近。也就是说结构元素尺寸在不同采样点数的螺纹轮廓信号上有较广的适用范围。经测试实验室测得的螺纹轮廓信号在牙顶或牙底处采样点一般不能少于5个点，所以选择5作为结构元素尺寸在保证滤波效果的同时还有较广的适用范围。

2  效果评价与结果分析

2.1  滤波效果评价

滤波效果评价指标一般包括：均方根误差（RMSE）、信噪比（SNR）。

均方根误差是预测值与真实值偏差的平方与观测次数n比值的平方根如式（8）。它是用来衡量观测值同真值之间的偏差，一般而言，均方根误差是指滤波后信号与原信号的均方误差，体现了信号的细节滤波情况，均方根误差越小，表示滤波效果均方根误差越小，表示滤波效果越好[17]。

均方根误差计算公式：

在评价滤波效果边缘保护能力上，采用提取每个牙形拐角处的5个点如图4所示来进行计算边缘均方根误差，以此衡量滤波方法的边缘保护性。

信噪比是指原始信号能量与噪声能量的比值，体现了噪声信号对于整体信息的影响，信噪比越高，滤波效果越好。

2.2  仿真结果与分析

选择结构元素尺寸为5的扁平结构元素对仿真螺纹进行滤波处理后，与其他四种提到的常见滤波方法在反复试验选取最佳滤波条件滤波后的效果进行比较，某牙局部效果图如图5所示，具体各方法滤波效果评价指标数值如表1所示。

由图5局部效果图以及表1中评价指标的对比可以看出，高斯滤波、平滑滤波、中值滤波等在螺纹牙形的拐角处虽然保持了线条的连续性，但是边缘破坏十分严重，造成误差偏大。小波滤波这里通过反复试验选用的是小波基为Haar的小波，由于该小波基函数为阶梯状，比较接近此次仿真实验螺纹的外形，所以滤波效果相对较好，但是在光滑区域用Haar小波处理时表现也会出现阶梯状，用它来逼近连续信号效果不是很好，同时上述几种方法在参数准确选取方面比较困难。而数学形态学滤波能在有效的滤除螺纹轮廓信号噪声的同时，保护螺纹轮廓的边缘，滤波后的信号能很好的接近原始轮廓。相比其他四种滤波方法，形态学滤方法在螺纹轮廓信号滤波效果，边缘保护，以及参数选取方面都具有比较大的优势。

2.3  实测螺纹轮廓滤波效果

图6给出的是一段实际测得的原始螺纹轮廓某一侧的轮廓点云信号，用本文滤波方法处理后可以看出该方法在实际使用中能有效滤除原始螺纹轮廓中的尖峰毛刺噪声，填补裂缝，很好的贴合边缘，也保证了线条的连续性，为后续轮廓拟合，参数计算提供便利。

3  结论

本文将数学形态学运用到一维螺纹轮廓曲线的滤波中，根据螺纹特点选用了扁平结构元素，根据螺纹轮廓牙形采样点选取适当的结构元素长度，然后用matlab模拟含噪螺纹曲线，对其进行滤波仿真。通过与其他常见的四种不同滤波方法滤波后的均方根误差和信噪比来对滤波效果进行评价，结果表明数学形态学滤波方法对期望的螺纹轮廓形狀表现出了较好的逼近效果，在提高信噪比的同时，也很好的保护了螺纹牙形边缘，而且滤波参数的选取比其他方法简单，参数适应范围广，具有可实用性。

参考文献

[1]孙淑琴， 刘骏妍， 蒋川东， 等. 最小二乘权值平滑滤波技术在核磁共振信号处理中的应用[J]. 吉林大学学报（工学版）， 2016， 46（3）： 985-995.

[2]ISO 16610-21： Geometrical Product Specifications （GPS）- Filtration-Part 21： Linear Profile Filters： Gaussian Filter[S]. Geneva： ISO， 2011.

[3]张静， 刘景夏， 林莹. 表面粗糙度测量中的稳健样条滤波算法[J]. 工具技术， 2011， 45（8）： 97-99.

[4]刘国宏， 郭文明.改进的中值滤波去噪算法应用分析[J].计算机工程与应用， 2010， 46（10）： 187-189.

[5]任志英， 高诚辉， 申丁， 等. 双树复小波稳健滤波在工程表面粗糙度评定中的应用[J].光学精密工程， 2014， 22（7）： 1820-1827.

[6]王晓强， 李艳娜， 崔凤奎， 等. 基于二代小波的表面粗糙度信息提取[J]. 河南科技大学学报（自然科学版）， 2015， 36（3）： 14-17+5.

[7]李兵， 张培林， 米双山， 等. 基于数学形态学的分形维数计算及在轴承故障诊断中的应用[J]. 振动与冲击， 2010， 29（5）： 191-194

[8]李春枝， 何建荣， 田光明. 数学形态滤波在振动信号分析中的应用研究[J]. 计算机工程与科学， 2008， 30（9）： 126-128

[9]王书涛， 张金敏， 李圆圆， 等. 基于数学形态学和模糊聚类的旋转机械故障诊断[J]. 仪器仪表学报， 2012， 33（5）： 1055-1061.

[10]孙敬敬. 数学形态学在振动信号处理中的应用研究[D]. 华北电力大学（保定）华北电力大学， 2012.

[11]Maragos P， Schafer R W. Morphological filters--Part II： Their relations to median， order-statistic， and stack filters[J]. IEEE Transactions on Acoustics Speech & Signal Processing， 1987， 35（8）： 1170-1184.

[12]王续东， 曲延滨. 基于多级广义自适应形态学滤波的电力信号消噪[J]. 电测与仪表， 2014， 51（11）： 45-49.

[13]王建东， 马增强， 李延忠， 等. 一种自适应调整滤波参数的轴承故障诊断方法[J]. 噪声与振动控制， 2017， 37（1）： 137-141.

[14]Dong Ya-bin， Liao Ming-fu， Fault diagnosis of rolling element bearing based on modified morphological method[J]. Mechanical Systems and Signal Processing， 2011， 25（4）： 1276-1286.

[15]Zhang Li-jun， Xu Jin-wu， Yang Jian-hong. Multiscale morphology analysis and its application to fault diagnosis[J]. Mechanical Systems and Signal Processing， 2015， 22（3）： 597-610.

[16]姜万录， 郑直， 朱勇， 等. 基于最优扁平型结构元素长度的液压泵故障诊断研究[J]. 振动与冲击， 2014， 33（15）： 35-41.

[17]郝建军， 刘勇刚， 廖刚， 等. 一种改进小波阈值函数的信号去噪[J]. 重庆理工大学学报（自然科学）， 2019， 33（4）： 93-97.