基于混合元启发式算法优化神经网络的热舒适度预测模型
朱婵
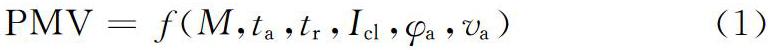


摘 要:热舒适度指标的计算过程具有多参数、非线性、高复杂度等特点,致使空调的实时控制器无法直接使用。针对这一问题,提出了一种基于混合元启发式算法神经网络的热舒适度预测模型:GACS神经网络。其中,GACS算法是一类融合了遗传算法和布谷鸟搜索的混合元启发式算法。仿真实验表明:与遗传算法相比,GACS算法在全局搜索能力方面得到了极大提升,其优化出的GACS神经网络具有更高的预测精度。
关键词:热舒适度;PMV指标;神经网络;遗传算法;布谷鸟算法
中图分类号:TP311
文献标志码:A
文章编号:1007-757X(2020)11-0066-04
Abstract:The calculation process of thermal comfort index has the characteristics of multi-parameters, non-linearity and high complexity, which makes the real-time controller of air conditioning unable to be used directly. To solve this problem, a thermal comfort prediction model based on hybrid meta-heuristic algorithm and neural network is proposed, i.e., GACS neural network. GACS is a hybrid meta-heuristic algorithm, it combines genetic algorithm and Cuckoo search. The simulation results show that compared with genetic algorithm, GACS algorithm has greatly improved the global search ability, and the optimized GACS neural network has higher prediction accuracy.
Key words:comfort;PMV index;neural network;genetic algorithm;Cuckoo search
0 引言
目前,大型建筑物内的空调控制方案大多以恒温控制为主,这不仅无法满足用户对热舒适度的多样化需求,还导致了不必要的能源消耗。上世纪60年代,丹麦工业大学的Franger教授提出了热舒适度方程,该方程可根据环境参数和人类活动情况综合计算出人体的热舒适度指标(Predicted Mean Vote,PMV指标)[1]。1984年,国际标准化组织(ISO)根据Franger教授的研究成果制订了ISO7730标准,即《适中的热环境——PMV与PPD指标的确定及热舒适条件的确定》[2]。热舒适度方程表明:人体舒适度与人类活动、衣着、空气温度、湿度、风速等多方面因素有关,因此,根据实际场景灵活调整空调的设定,可以在保证舒适度的前提下,有效降低空调能耗[3]。但热舒适度方程的计算具有多参数、非线性、高复杂度等特点,而空调实时控制器结构简单,无法完成计算[4]。2002年,高立新、白桦等人提出利用BP神经网络构建PMV快速预测模型,仿真实验表明,该模型的预测准確率在95%以上,完全能够满足空调实时控制系统的要求[5]。此后,研究者们通过不同途径优化预测模型,不断提高预测精度。2010年,徐巍、陈祥光等人提出利用遗传算法和BP神经网络相结合的方式优化室内热舒适控制参数,大幅度提高了算法的预测效率[6];2014年,张玲、王玲等人提出利用改进的粒子群算法优化BP神经网络的热舒适度预测模型,该方案改善了对网络初始值敏感的问题,同时有效提高了预测精度,其预测误差仅为9×10-4[7];2015年,闫婷在其硕士论文中,提出利用蚁群算法优化BP神经网络,其预测正确率达到了99.88%[8];
2018年,郭彤颖,陈露等人提出利用鸟群算法优化基于BP神经网络的热舒适度预测模型,该模型较粒子群算法在收敛速度和预测精度上均有提升[9]。已有的研究表明,BP神经网络经过多次训练可有效提高预测的精度,然而,其预测结果严重依赖随机生成的网络初始参数。通过遗传算法优化后的神经网络在预测稳定性方面大大提高,但遗传算法本身全局搜索能力的欠缺又导致预测结果容易陷入局部最优[10]。为此,
本文将利用遗传算法和布谷鸟算法构建混合元启发式算法优化神经网络,再利用改进后的网络建立PMV预测模型,仿真实验表明该预测模型能准确地预测PMV指标,其最佳预测误差仅为8.7×10-5。
2 热舒适度的预测平均投票模型
预测平均投票模型中主要涉及到四个环境因素和两个人类活动因素,其中环境因素包括空气温度ta、平均辐射温度tr、空气相对湿度φa和风速va;人类活动因素包括人体新陈代谢率M和服装热阻Icl。因此,当人体做功为0时,PMV指标可由式1所示的函数形式表出,具体计算方法在参考文献[1]中有详细描述,如式(1)。
PMV指标的计算结果代表了大多数人在环境中的冷热感受,其取值通常在-3到3之间,整数值的具体含义ISO7730认定热舒适环境应保证其PMV取值位于-0.5到0.5之间[2],如表1所示。
3 BP神经网络与混合元启发式算法
3.1 BP神经网络
BP神经网络全称为Error Back Propagation Network,即误差反向传播网络,是目前理论体系最为完善、应用最为广泛的算法模型。其特点是在训练网络时,根据输出结果的误差,从输出层开始逐层向前修正权值、阈值以达到降低误差的目的[11]。本文采用的BP神经网络为三层结构,如图1所示。
其中,第一层为输入层包含6个神经元,分别表示人体新陈代谢率、空气温度、平均辐射温度、服装热阻、空气相对湿度和空气流速;第二层为隐含层包含16个神经元,训练函数为logsig( );第三层为输出层包含1个神经元表示PMV指标, 训练函数为purelin( )。
3.2 GACS算法
GACS(Genetic Algorithm-Cuckoo Search,GACS算法)是一类混合元启发式算法,目前常见的元启发式算法有遗传算法、禁忌搜索、粒子群算法、布谷鸟搜索和蚁群优化算法等。这类算法通常基于一种仿生策略,通过反复迭代搜索找出最优解,但根据策略的不同,算法各有优缺点。因此在算法之间取长补短重新构成出一种寻优能力更强、搜索效率更高的混合算法是目前元启发式算法研究的重点[12]。本文提出的GACS算法由遗传算法(Genetic Algorithm,GA)和布谷鸟搜索(Cuckoo Search,CS)混合而成。其中,遗传算法于上世纪六十年代由美国密歇根大学的 Holland教授提出,算法通过模拟自然界优胜劣汰的进化机制,对随机生成的解集进行反复迭代搜索,最终找出最优解。由于算法具有高度的并行性且通用性强,因此在各行各业都得到了广泛应用[13]。布谷鸟搜索由剑桥大学的Xin-She Yang、Suash Deb于2009年提出,该算法模拟了布谷鸟的寄生育雏和Lévy飞行机制,通过长、短距离飞行交替进行的方式,使得算法具备了卓越的全局搜索能力[14]。本文在遗传算法中加入布谷鸟搜索机制,将改善遗传算法全局搜索能力较弱,容易陷入早熟的问题,算法流程如图2所示。
算法的主要步骤如下。
步骤一:利用BP神经网络生成的初始化种群,其个体由BP网络的初始权值、阈值构成;
步骤二:将个体所对应的BP神经网络预测精度作为其个体适应度;
步骤三:依次执行遗传算法的选择、交叉、变异操作;
步骤四:选取适应度较低的20%的个体进行布谷鸟搜索;
步骤五:判断是否满足遗传迭代的停止条件,满足则输出搜索结果,不满足则跳转至第二步。
下面就GACS算法中的几个重要部分进行详细阐述。
(1) 初始种群与个体:GACS算法的优化对象为BP神经网络的权值和阈值,种群中的一个个体对应一种网络的结构,初始种群由随机生成的N个BP网络训练而来,即种群规模为N。任意个体Xi采用二进制编码,其长度L=(I×H+O×H+O)×P,其中I、H、O为输入层、隐含层、输出层的神经元数量,P为权值和阈值的二进制位数。
(2) 个体适应度:一个个体对应一组BP神经网络的权值阈值组合即网络结构,个体适应度等于该网络预测出的PMV值与实际取值的绝对误差值,即适应度越低表示该个体越靠近最佳解。
(3) 遗传操作:在遗传算法中选择、交叉、变异操作合称遗传操作,每次迭代都会对种群依次执行所有遗传操作。GACS算法中,遗传操作为随机遍历抽样,代沟值为0.9;交叉操作为单点交叉,交叉概率为0.7;变异操作为离散变异,变异概率为0.7Lind,其中Lind为个体的长度L。
(4) 布谷鸟搜索:在完成遗传操作后,按种群规模的20%选取适应度较的个体集合进行布谷鸟搜索,搜索中将依序执行以下三步操作。
步骤一:利用Lévy飞行模拟找寻新巢的过程即产生新的个体集,Lévy飞行[14]的具体操作,如式(2)。
式中,Xt+1为新个体集;Xt为旧个体集;α为飞行步长,通常取值为1;levy(β)为Lévy随机路径,β通常取值为1.5。
步骤二:选取新个体集中前10%的优势个体替换旧个体集中的劣势个体,从而构建出新的种群。
步骤三:模拟宿主发现寄生行为的过程,以25%的概率pa抛弃种群中的劣势个体,并随机生成新个体用以替换,新个体的产生方式[14],如式(3)。
式中,Xt+1为新个体集;Xt为旧个体集;r、ε为服从均匀分布的随机数;Heaviside()为单位阶跃函数函数;pa为抛弃概率,取值为0.25;xi、xj为任意个体。
3.3 GACS神经网络
BP神经网络具有高度复杂的非线性结构,容易导致内部出现多个局部极值点。同时,网络训练结果严重依赖系统随机生成的权值和阈值[11]。为提升网络的全局搜索能力和预测精度,本文在确定神经网络的拓扑结构后,利用GACS算法优化神经网络的权值和阈值,再通过梯度下降法对GACS算法的优化结果进行补充训练,最终找出预测精度最高的热舒适度预测模型,GACS神经网络执行流程,如图3所示。
GACS神经网络执行流程如下。
步骤一:确定神经网络的拓扑结构,如图1所示;
步骤二:初始化种群,种群由BP神经网络训练而来,一个个体代表一种网络结构;
步骤三:计算个体适应度;
步骤四:执行遗传操作;
步骤五:执行布谷鸟搜索;
步骤六:判断是否滿足迭代的停止条件,满足进入下一步,不满足跳转至第三步;
步骤七:利用梯度下降法对种群进行最后一次优化;
步骤八:算法结束,输出预测结果。
4 仿真实验及数据分析
为验证GACS神经网络的预测精度,本文随机生成了700组参数组合,并根据Fanger教授的热舒适度方程计算其PMV指标,其中,600组作为训练样本,100组作为测试样本。相关参数的取值范围分别是:人体新陈代谢率M为36~200 W/m2、空气温度ta为20~35 ℃、平均辐射温度tr为10~40 ℃、服装热阻Icl为0~1clo、空气相对湿度φa为30~70%、空气流速va为0~1 m/s。仿真实验平台为MATLAB R2015a,通过编程分别实现了基于GA神经网络和基于GACS神经网络的热舒适度预测模型。实验中,算法种群规模为600,迭代次数为500,两种网络的种群均值变化过程如图4、图5所示。
最优解的搜索过程如图6、图7所示。
图4和图5分别展示了GA神经网络和GACS神经网络在500次迭代过程中,种群均值的变化过程。GA神经网络的种群均值在第11代时获得了3 641的峰值,之后迅速收缩,从第20代起,基本徘徊在2 300以下的区间。GACS神经网络则在第74代时,种群均值依然达到了3 497的高位取值,并且在250代到400代之间,其均值仍多次接近3 000。可见,GACS神经网络利用布谷鸟的Lévy飞行机制,在迭代过程中很好的保持了个体多样性大幅提高了算法的全局搜索能力,有效避免了算法早熟。
图6和图7分别展示了GA神经网络和GACS神经网络在500次迭代过程中,最优解的搜索过程。GA神经网络的最优解取值在第51代时降至0.06,第269代时降至0.05,最终在第500代时降至0.048。GACS神经网络的最优解取值则在初期就得到了较快收敛,在第18代时就降至0.04,第160代时降至0.36,最终在第500代时降至0.35。可见,GACS神经网络在最优解的搜索过程中,得到了更为精确的预测模型,如图8所示。
选取了GACS神经网络预测结果中的100个个体 ,以此为例,展示了基于GACS神经网络的热舒适度模型的预测值与实际PMV取值的对比结果。经计算,GACS神经网络的最佳预测精度达到了8.7×10-5。在该精度下,预测模型可更为精确的预测当前环境的热舒适度,从而为建筑空调运行提供更为优化的节能运行方案。
5 总结
本文依据Fanger教授提供的热舒适度方程,提出一类基于混合元启发式算法的热舒适度神经网络预测模型。其中,用于优化神经网络的混合元启发式算法为GACS算法,该算法在遗传迭代中融入了布谷鸟搜索,有效提高了全局搜索能力,其最佳预测精度达到了8.7×10-5。但在研究中还存在诸多不足之处,例如:由于GACS算法添加了布谷鸟搜索,其运行过程中需多次计算个体适应度,导致其搜索速度大大降低;另外,本文中遗传算法采用的是二进制,而布谷鸟搜索是十进制,使得每次迭代中均需要进行十进制和二进制的相互转换,进一步影响了整体算法的运行效率。因此,在后续研究中,还需不断深入研究,在提高GACS神经网络预测精度的同时,提升其搜索的效率。
参考文献
[1] 朱颖心. 建筑环境学[M]. 北京:中国建筑工业出版社,2016:94-140.
[2] ISO. International Standard 7730. Moderate thermal environment-determination of the PMV and PPD indices and specification of the conditions for thermal comfort [S]. Geneva:International Standard Organization, 1984.
[3] 鐘潇. 基于热舒适度的建筑空调用电优化研究[D]. 华北电力大学,2016.
[4] Jian Yao, Jin Xu. Research on the BPNN in the prediction of PMV[J]. Applied Mechanics and Materials,2010,29(32):2804-2808.
[5] 高立新,白桦. 利用神经网络预测PMV指标[J]. 北京:哈尔滨建筑大学学报,2002,35(5):70-72.
[6] 徐巍,陈祥光,彭红星.基于神经网络和遗传算法优化室内热舒适控制参数[J].北京理工大学学报,2010,30(2):240-244.
[7] 张玲,王玲,吴桐. 基于改进的粒子群算法优化反向传播神经网络的热舒适度预测模型[J]. 计算机应用,2014,34(3):775-779.
[8] 闫婷. 基于蚁群与神经网络算法的变风量空调末端控制研究[D].西安建筑科技大学,2015.
[9] 郭彤颖,陈露.基于鸟群算法优化BP神经网络的热舒适度预测[J].计算机系统应用,2018,27(4):162-166.
[10] 周毅.以热舒适度为目标的室内空调环境建模、优化与仿真研究[J].自动化应用,2017(12):13-15.
[11] 陈明. MATLAB神经网络原理与实例精解[M]. 北京:清华大学出版社,2012:156-191.
[12] 徐俊杰. 元启发式算法:理论阐释与应用[D]. 合肥:中国科学技术大学出版社, 2015.
[13] 雷英杰,张善文,李续武,等. MATLAB遗传算法工具箱及应用[M]. 西安:西安电子科技大学出版社,2005:1-8.
[14] 黄继达. 布谷鸟算法的改进及其应用研究[D].武汉:华中科技大学,2014.
(收稿日期:2019.08.29)

