火炮对空中目标射击弹道解算方法分析

任华杰，张瀚巍，冀志轩

（1.海装沈阳局驻沈阳地区第三军事代表室，沈阳110045；2.海装沈阳局驻沈阳地区第四军事代表室，沈阳110021；3.海装沈阳局，沈阳110031）

0 引 言

现代战争中，武器系统发现空中目标后的反应时间往往决定防空作战的胜负，而火控系统则是武器系统必不可少的重要组成部分，是武器系统的“大脑”和“眼睛”，准确、实时地计算出射击诸元，并将其赋予武器以将弹头准确送抵目标区域，是火控系统的核心任务。而对于坦克或舰船上的火控系统[1]而言，能否对空中目标进行准确的弹道分析决定了能否在有限时间内计算出导弹轨迹进而准确击毁目标。

本文以舰艇火控系统为研究对象，详细讨论了各种方法的优缺点，以及所选择的技术对弹道建模的帮助。火控计算机在光电火控系统中的作用是通过伺服接口单元将计算出的俯仰角和方位角传输给舰艇主炮。俯仰角和方位角包括弹道偏移量和导程角。而弹道偏移量大小与武器平台和弹药特性有关[2]。火控计算机的输入是目标的距离、垂直角度和水平角度(R,θ,φ)及其他计量参数，如气温、气压、风速等。

火控计算机需要控制所有的计算并为瞄准系统和火炮伺服提供接口，而瞄准系统和火控计算机是通过串行接口连接。

1 弹道解算

弹道算法是在标准数据表的基础上发展起来的。标准数据表包括武器/弹药特性、标准条件、射程与仰角的对应关系及标准条件变化的修正表。

针对特定弹药开发弹道算法[3]的步骤如下：1）通过弹道仿真分析标准数据表；2）用标准数据表验证弹道模型；3）开发火控计算模型。

2 通过迭代算法追踪目标

迭代算法是所有运动目标定位技术中常用的一种方法。火控计算机的软件负责驱动控制器硬件，也负责计算弹道偏移量和导程角[3]。因此，目标跟踪和确定目标距离是火控计算中非常重要的一部分。我们首先假设一个空中目标等速模型(即直升机、飞机)，然后选择极坐标系[4]。在所有方法中，输入数据(R,θ,φ)都是相同的。其中(R,θ,φ)分别为目标距离、垂直角和水平角。由单一来源提供相同的数据可用于分析不同的方法。

在迭代算法中确定目标(R,θ,φ)值，需要距离和角度传感器测量出至少2 个点的数值，然后通过在观测点测量时间可以计算出目标速度。接下来我们在模型分析上把极坐标系转换为笛卡尔坐标系。目标会从T1时刻飞到T2时刻，再飞到T3时刻，而T2时刻可以通过标准弹道表和误差补偿确定，然后这个计算过程再次循环，直到炮弹和目标的飞行时间在某一位置重合。设(x1，y1，z1)为目标当前位置坐标，为t1时刻，(x2，y2，z2) 为目标下一位置坐标，为t2时刻，可通过以下关系确定: Δt1=T2-T1；x2=x1+Vx·Δt1；y2=y1+Vy·Δt1；z2=z1+Vz·Δt1。其中，Vx、Vy和Vz是坐标系3 个方向上的速度分量。

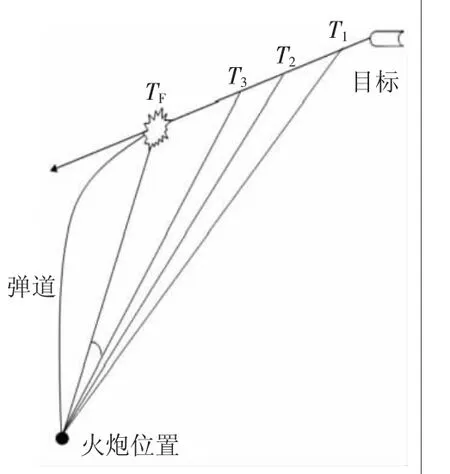
图1 迭代模拟过程

3 火控计算机不同的计算方法

1）时间最短的计算方法。在这个模型中，我们基于最短的时间击毁目标。根据目标的当前位置，我们可以用某个标准的零时刻快速计算出下一时刻目标位置和飞行时间。当目标到达预定位置时，炮弹已经提前发射，确保实现目标打击。击落目标的时刻=当前发现目标时刻+炮弹飞行时间+射击时间+计算时间+射手反应时间。在这个计算方法中，击毁目标的攻击距离为发现目标距离的一半，且满足：TOF(target)-[TOF(projectile)+arbitrary time]=0.01。

如图2 所示，r2=r1/2。该模型适用于打击目标时间最短方案，但是武器射程需要前期考虑选择最短路径。

2）距离最短计算方法。在这个计算方法中，视线与目标轨迹的切线之间垂直于该点的角度称为最近点。炮弹在目标和火炮之间的距离最短的情况下发射。在这种情况下，命中概率是非常好的，因为散布很小。但这个方法只考虑了射击命中率，没考虑来袭目标，因为等待目标到达最近的点涉及更大的安全风险。

3）预选距离计算方法。在这个计算方法中，预选距离应大于最小射击距离，但小于目标跟踪距离，所有的计算都是基于预先选定目标距离进行的，因此我们必须计算出目标所有可能的来袭方向，否则就很难攻击目标。因为弹道计算已经提前对选定的杀伤距离进行了计算，所以这个方法对于高速来袭目标是一种非常有用的方法。一旦目标从预先选定的方向进入拦截范围，应确保目标飞行时间和炮弹飞行时间在交汇点是一致的。

4 讨 论

通过建立起跟踪距离与杀伤距离之间的关系，表明实际弹道与计算弹道之间存在着差异。假设我们把瞄准系统安装在射程为8000 m 的大炮上，目标追踪从8000 m开始。为了达到预期的拦截效果，根据理论数学模型的结论[5]，杀伤距离应该是跟踪距离的一半。表1 及表2 列出两种情况下不同距离、目标速度和飞行高度的跟踪距离和视角的比较数据（假设目标在水平方向移动）。

情况1：跟踪距离为8000 m，飞行时间为10 s，目标飞行速度为250 m/s，目标垂直高度为2500 m。

图2 时间最短计算模型

表1 目标速度250 m/s的距离、角度、时间变化表

情况2：跟踪距离为8000 m，飞行时间为10 s，目标飞行速度为350 m/s，目标垂直高度为2500 m。

因为炮口初速误差有1%，空气密度变化有10%，风速变化有10 m/s，以及不同仰角所受横风的不同，标准数据表需要对弹丸在飞行中水平距离、飞行高度和方位角进行校正。

假设当前时间=a，炮手反应时间=b，火炮定位时间=c，弹道解算时间=d，则杀伤时间=炮弹的飞行时间+a+b+c+d。

针对情况1，使用最短时间方法：杀伤距离=7666.6/2≈4000 m，炮弹的飞行时间+a+b+c+d=7.7 s。使用预选距离计算方法：3.6 s＜炮弹的飞行时间+a+b+c+d＜10 s。使用距离最短计算方法：7.7 s＜炮弹的飞行时间+a+b+c+d＜10 s。因此，使用最短时间方法和预选距离方法对于平均速度为250 m/s 的目标命中效果较好。因为如表1 所示，在4000 m 处的目标指向角度为38.6°，所以我们有足够的时间摧毁目标。

针对情况2，使用最短时间方法：杀伤距离=8000/2=4000 m，

炮弹的飞行时间+a+b+c+d=7.7 s。使用预选距离计算方法：3.6 s＜炮弹的飞行时间+a+b+c+d＜10 s。使用距离最短计算方法：7.7 s＜炮弹的飞行时间+a+b+c+d＜10 s。因此，最短时间技术并不适用于高速目标。如表2 所示，在4000 m 处的目标指向角度为48.6°，在这种情况下我们没有太多的时间去打击移动目标。而预选距离技术对打击高速目标有很好的效果。

表2 目标速度350 m/s的距离、角度、时间变化表

5 结 语

通过对这些技术的分析和研究，有助于设计基于目标速度、方向和飞行时间的火炮超前角计算软件。上述方法有助于计算某一特定射程和大气条件下火炮的超高和超方位角(弹道偏移量)及飞行时间。弹道解算方法的选择取决于目标的特征。分析结果表明，对于平均速度目标，可以采用最短时间方法或预选距离方法，但对于快速移动目标，只有预选距离方法效果最好，最近点技术方法的安全风险较大。