两种制导侵彻火箭弹火力分配研究

房施东，杨清文*，孟凡凯，孙吉红，李 鑫

（1.陆军炮兵防空兵学院，合肥 230031；2.解放军77115 部队，四川 崇州 611230）

0 引言

火力分配是火箭炮作战使用的重要内容。火箭炮武器系统配备多种弹药，在遂行战斗任务时，需要选取一种或几种合适类型的弹药进行打击。因而火箭炮火力分配问题的研究备受关注，例如，邢立新等人［1］根据最有利的火力分配原则建立了线膛炮与火箭炮重迭射击时的火力分配方法；李臣明等人［2］研究了箱式火箭炮对面目标进行杀伤时的最优火力分配方法；王兆胜［3］研究了子弹均匀散布子母弹最有利火力分配方法。

末制导侵彻火箭弹战斗部为侵彻战斗部［4］，与已有的制导侵彻弹用途基本一致，作战使用时，两者的选择难度较大；同时，与之相关的火力分配问题的研究目前尚属空白。因而开展此两种火箭弹之间的火力分配问题研究，为火箭炮作战使用提供参考。首先根据远程火箭炮作战任务特点构建火力分配模型；然后进行计算分析，以获取目标特性对弹药消耗费用的影响规律，为火力分配提供参考；最后基于构建的模型对典型目标进行火力分配计算分析与仿真验证。

1 模型构建

1.1 模型构建的基本内容

构建火力分配模型主要考虑武器单元特征、目标单元特征、最优准则、射击条件、多约束条件等［5］。具体如表1 所示。

表1 火力分配模型构建的基本内容

1.2 基本假设

基本假设:我方基于远程火箭炮1 种发射平台，有n 类弹药，敌方有m 个目标，则定义如下变量:ci（i=1，…，n）为该类弹药储备数量；ei为第i 类弹药单价；Nij为我方第i 类弹药对敌第j 个目标的发射弹药数量（i=1，…，n；j =1，…，m）；Pijd为第i 类单发火箭弹对敌第j 个目标命中概率；Hijd为第i 类单发火箭弹对敌第j 个目标的毁伤概率；Hij为发射的第i类火箭弹对第j 类目标的全体毁伤概率；Hj为发射的全部弹药对第j 类目标的全体毁伤概率。

1.3 极小化弹药消耗费用模型

在远程火箭炮实际的作战过程中，一般情况下都是上级确定打击目标和打击期望，作为火力单元而言，主要分析如何以最小的弹药消耗费用完成上级的任务［6］。因此，主要构建极小化弹药消耗费用模型，具体如下:

式中，PE（0＜PE＜1）为打击期望；G（k）为毁伤律，对于末制导侵彻火箭弹，主要打击对象为坚硬小目标，因此，可以选用指数毁伤律［7］:

式中，k 为命中的弹数，a 为易损区（相对）面积。

通过极小化弹药消耗费用模型可以看出，关键是两种火箭弹对目标命中概率的计算。

1.4 命中概率计算模型

图中自寻的火箭弹与普通制导火箭弹弹道特性不同，其命中概率计算方法差异较大，因此，分别进行构建其命中概率计算模型。

1.4.1 普通制导火箭弹

设普通制导火箭弹的单发命中概率为P1jd，目标幅员的正面和纵深分别为2Lz 和2Lx，假设落点偏差符合正态分布［8］，则根据弹着点的联合概率密度函数得其命中概率计算公式［9］:

式中，μx，μz分别为落点散布中心在x 向和z 向离目标点的平均距离，表征落点系统误差；σx，σz分别为纵向、横向落点的标准偏差，表征落点散布误差。

1.4.2 末制导侵彻火箭弹

末制导侵彻火箭弹交班成功率是其命中精度的重要影响因素，因而计算时需要考虑交班成功和交班失败两种情况。设末制导侵彻火箭弹的单发命中概率为P2jd，末制导侵彻火箭弹交班成功概率为Pjiao，交班成功后末段命中概率为Pmo；另外，在此认为，若末制导侵彻火箭弹交班失败，其命中概率与普通制导火箭弹的单发命中概率P1jd相同。则末制导侵彻火箭弹单发命中概率P2jd:

式中，Pjiao由末制导侵彻火箭弹性能确定，Pmo由交班成功后火箭弹落点的系统误差和散布误差决定，计算方法同式（3）。

2 计算分析

上述两种火箭弹都配备侵彻战斗部，打击目标性质基本一致，主要打击坚固工事或停泊的舰船等目标，因此，目标性质因对火力分配影响不大；同时，打击目标基本都为静止目标，在此也不考虑速度影响。因此，在此主要分析目标幅员与定位误差这两项影响较大的因素。定性分析可知，末制导侵彻火箭弹的优势是精度更高，对目标定位精度要求较低，适合较小目标的打击；而普通制导侵彻弹的优势是价格较低，更适合较大目标的打击，且对目标定位要求较高。因此，定量计算的关键是，根据两种火箭弹命中概率，获取目标定位精度、幅员等因素对弹药消耗费用的影响规律，从而为费用极小化的火力分配提供依据。

2.1 单发命中概率计算分析

对于普通制导火箭弹，由于其系统误差较小［10-11］，因此，根据工程经验，当σx=σz时，可得:σx=σz=0.85×CEP；同时目标定位误差可以作为系统误差处理［10］。对于末制导侵彻火箭弹，在交班成功的条件下，根据相关文献［11］对末制导侵彻火箭弹命中概率仿真计算结果，可取μx=1.6 m，μz=1.7 m，σx=σz=3.4 m；若交班失败，其特性则与普通制导侵彻火箭弹类似。

根据上述数据和命中概率计算模型可得两种火箭弹的单发命中概率Pijd随目标幅员和定位误差变化规律，如图1 所示。

通过图1 可以看出，两种火箭弹单发命中概率都与目标幅员成正比，与定位精度成反比；当目标幅员较小时，末制导侵彻火箭弹命中概率明显大于普通制导侵彻弹，随着目标幅员的增大，优势逐渐减小，最终命中概率基本趋于一致；同时，末制导侵彻火箭弹受目标定位精度影响较小，但是普通制导火箭弹受目标定位误差影响较大。

2.2 弹药消耗量计算分析

假设目标易损区a 值为1，则命中一发即毁伤。打击预期PE要达到0.8，则两种火箭弹需要的弹药消耗量比例（末制导侵彻火箭弹/普通制导火箭弹）如图2 所示。

通过图2 看出，目标幅员较小时，普通制导火箭弹需要的弹药消耗量明显大于末制导侵彻火箭弹，随着幅员的增大，普通制导火箭弹消耗量迅速减少，在目标的距离与方向定位误差都不大于60 m的情况下，当幅员大于180 m×180 m 时，两者弹药消耗量一致。同时，定位误差对弹药消耗量影响也较大，定位误差越大，普通制导火箭弹命中概率越小，弹药消耗量越大，两者弹药消耗量比也就越小。

图1 Pijd 随目标幅员和定位误差变化曲线

图2 弹药消耗比变化曲线

2.3 弹药费用计算分析

由于不同的弹种生产成本不同，因此，在弹药消耗量计算的基础上来计算所需费用，以此来分配火力。假设单发末制导侵彻火箭弹成本是普通制导火箭弹的1.2 倍。则依据弹药消耗量计算的费用比（费用比=末制导侵彻火箭弹总费用/普通制导火箭弹总费用）如图3 所示。

图3 两种火箭弹的费用比变化曲线

通过图3 看出，其变化规律与弹药消耗量比基本一致。根据上图可得不同定位误差条件下费用比为1.0（即两种火箭弹费用相同）时的目标幅员。因此，在已知目标定位误差和目标幅员的情况下，即可判断采用上述哪种火箭弹费用最低。

3 实例验证

3.1 目标假设

假设分配给远程火箭炮的任务目标有5 个，全部为混凝土目标，具体参数如表2 所示。

表2 分配给远程火箭炮的任务目标

3.2 分配方案确定

根据目标特点，假设目标易损区a 值为1，此时命中概率即为毁伤概率。根据上述目标定位精度、目标幅员，依据图1 两种火箭弹单发命中概率曲线，可得两种火箭弹对任务目标的单发命中概率Pijd矩阵，由于采用0-1 毁伤律，则单发毁伤概率Hijd矩阵即为Pijd矩阵:

根据图3 数据可知，对于幅员小于106 m×106 m的目标（M1001、M1002、M1003、M1004）采用末制导侵彻火箭弹比费用最小；对于幅员不小于106 m×106 m 的目标（M1005）采用目标，使用普通制导火箭弹费用最小。根据图3 还可以确定费用极小情况下打击各目标的弹药消耗量，具体如表3 所示（其中，弹种1 为末制导侵彻火箭弹，弹种2 为普通制导侵彻弹）。

表3 打击弹种分配及其最低弹药消耗量

根据表3 可知，要完成上级赋予的任务，需要末制导侵彻火箭弹10 发，普通制导火箭弹1 发。其弹药消耗Nij矩阵:

根据弹药消耗量，确定采用两门火箭炮分别进行射击，计划1 炮发射末制导侵彻火箭弹，2 炮发射普通制导火箭弹，具体火力分配如图4 所示。

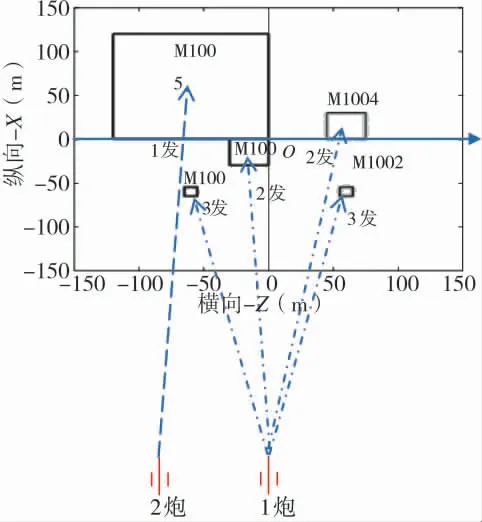
图4 两种火箭弹火力分配结果

3.3 毁伤计算与验证

3.3.1 毁伤计算

根据上述火力分配方案，由于目标分布较为密集，因此，须考虑火力重叠问题，如打击M1001 号目标的交班失败的火箭弹可能击中M1003 号目标。计算时将各目标中心的相对位置作为目标定位误差处理，假设图4 中O 点为坐标中心O（0，0），则各目标中心坐标分别为:M1001（-60，-60）、M1002（60，-60）M1003（-15，-15）、M1004（60，15）、M1005（-60，60）。计算得各目标中心相对坐标如表4 所示。

表4 各目标中心坐标及相对位置

根据上述目标相对位置与目标定位误差（X、Z方向各为20 m）和武器参数，在考虑火力重叠的情况下计算得两种火箭弹对各目标的毁伤概率矩阵如下:

则对各目标的整体毁伤概率矩阵如下:

可见，采用上述火力分配方案，在弹药消耗费用最少的情况下，对目标的毁伤效果达到了毁伤预期0.8 的要求。

3.3.2 毁伤验证

为了进一步验证基于上述火力分配的毁伤效果，基于MATLAB 运用蒙特卡洛法对落弹散布进行仿真，根据武器系统参数，运用蒙特卡洛法对每一目标的各打点500 次，炸点分布效果如图5 所示。

图5 两种火箭弹落点仿真

采用落点统计法计算落入目标区域的弹数，以此计算两种火箭弹对5 个目标的整体命中概率（即毁伤概率）:Hj=［0.837 0.853 0.939 0.935 0.919］，统计结果与理论计算结果基本一致，说明构建的火力分配模型科学准确。

4 结论

根据构建的费用极小化火力分配模型，通过计算分析获取了目标定位误差、目标幅员对末制导侵彻火箭弹和普通制导侵彻弹弹药消耗费用的影响规律，为两种弹药的火力分配提供了理论依据。最后进行了实例计算分析与仿真验证，结果显示，构建的火力分配模型符合实际，计算方便，能够满足作战任务需求，为火箭炮多弹种火力分配提供了参考。