基于投影变换判断导弹残骸落区安全性能的算法*

尤 浩 王 宁 赵久奋 彭 泉

（1.火箭军工程大学 西安 710025）（2.中国国际工程咨询有限公司 北京 100080）

1 引言

随着我国经济的日益发展，人口越来越稠密，地面的各种建筑物和设施不断增加，加上作战理论的丰富发展以及武器装备数量的增多，多导弹协同作战的方式已经逐渐成为目前战争的主要方式，多导弹协同作战带来的直接影响就是导弹残骸数量增多，相应地面规避区域人员、物资撤离难度加大、范围广，由此，对导弹残骸落区安全问题的研究日益必要［1］。

保障导弹残骸落区安全可以从将残骸落点控制在人烟稀少的地方和提高落区划定的精度，减小落点散布的范围这两方面入手［2］。

目前，关于残骸落区划定的文献较多，但对具体定量计算残骸落区和地面规避区域之间安全性的文献则相对较少。文献［3］通过坐标变换关系得出的运动学方程，它只讨论导弹运动的几何性质，不涉及产生运动和改变运动的原因，算出残骸落区精度较差。文献［4］则是以牛顿力学定律为基础的积分法，没有考虑空气阻力的影响，残骸落区覆盖范围较大。文献［5］对某发射卫星中心的历次火箭残骸落点数据进行了统计分析，基于分级预警思想，对不同预警区的危险系数进行了计算，但是该方法定义的预警区域范围较广，相应地面规避区域人员撤离工作量较大。文献［6］分析了残骸在下落过程中的动力学特性，提出了带空气阻力修正的残骸落点算法，较好地缩小了导弹残骸落区分布范围。文献［7］通过引进栅格翼气动性能分析法，大幅缩小了残骸落点的散布范围。

通过上述文献可知，现阶段，导弹残骸落区精度已经有了较大水平的提高，较大地减少了规避区域人员资产撤离的损失，但是目前还需要对所有在残骸落区范围内的规避区域进行人员物资撤离，当参与导弹数量很多时，损失任然很大。

针对上述问题，本文详细提出了一种导弹残骸落区和地面规避区域的位置关系判断的方法，在此基础上，通过构建二维正态分布模型定量快速计算导弹残骸落区多边形和规避区域多边形的交集区域概率，并将交集区域概率与设置阈值比较，从而选择性地选择相关规避区域人员和物资撤离，极大地减小了人力物力损失。

2 坐标的地球投影变换

2.1 坐标系的空间转换

假设地球是半径为R的一个空间球体，构建空间直角坐标系如图1所示：圆点位于空间圆球的中心，Z轴指向空间圆球的北极，X轴指向起始子午面与赤道的交点，Y轴位于赤道面上且按右手系与X轴呈90°夹角。某点在空间中的坐标可用该点在此坐标系的各个轴上的投影来表示［8］。

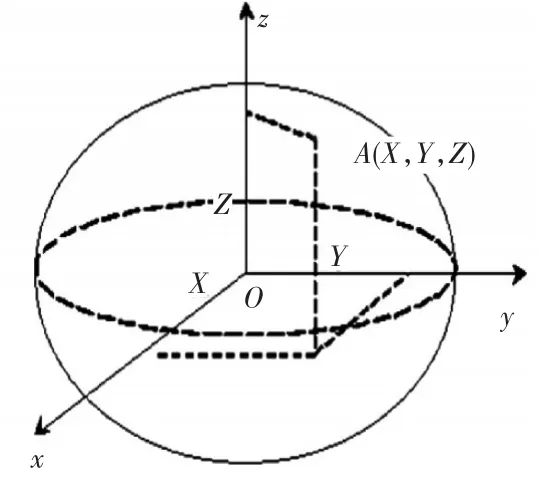
图1 空间直角坐标系示意图

设某点的经度为L，纬度为B，则该点的地理坐标和空间直角坐标的转换关系为

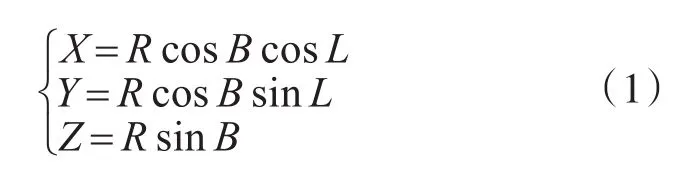
在投影变换前，需要将导弹残骸落区多边形和规避区域多边形的地理坐标系内的经纬度数据统一采用上述方法转换到三维空间直角坐标系。

2.2 残骸落区切平面方程的建立

在图1建立的空间直角坐标系内，已知球面上一点A=(x0，y0，z0)的坐标，则该点的切平面方程可用平面点法式方程表示，点法式的法线为

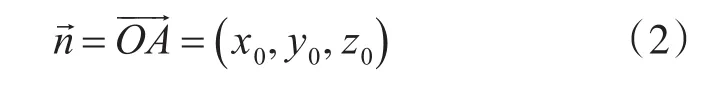
投影面的选择影响计算精度，只要在导弹残骸落区内任意选择一点做切平面，计算的误差相差不大。本文采用输入残骸落区多边形的第一个点做投影切平面，比较方便简单。

2.3 空间直角坐标系到切平面的投影

做直角坐标系上任意一点B=(xB，yB，zB)到切平面的垂线，则切平面上垂直投影点为B'，则：

投影点B'坐标计算如下：

2.4 切平面内的二维坐标系建立

投影变换的目的是把三维数据变换到二维平面内，便于计算，因此本文在投影的切平面内拟建立一个二维坐标系。二维坐标系的原点设为切点A=(x0，y0，z0)，设地球北极点在平面内的投影点为N=(xN，yN，zN)，取方向为X轴方向。不妨设在A点存在一个从球内指向球外的Z轴，则可由右手定则确定Y轴的方向。

Y轴方向：

对于切平面上任意一点B'=(xB'，yB'，zB')，其在二维坐标系下的坐标可表示为

通过上述几步计算即可以将地理坐标系以经纬度表示的点，投影到一个二维坐标系下的平面。由此，可快速计算出导弹残骸落区多边形和地面各规避区域多边形在投影平面上的二维坐标点。

3 快速判断两个多边形的交集区域

求解两个多边形的交集区域实际意义在于求解残骸落区与规避区域在二维坐标系内的相交区域［7～8］。

如图2所示，平面多边形1与平面多边形2相交，交集区域多边形表示为k1b2k4k3k2e1。可以发现交集区域多边形都是由不同折线段首尾拼接而成的。

通过观察可知，交集区域多边形的每条折线段都是由相交的点和相包含的点组成。由此，本文将快速判断两个多边形的交集区域分解为以下三个过程：图形预处理，求取交集折线段，拼接交集折线段。

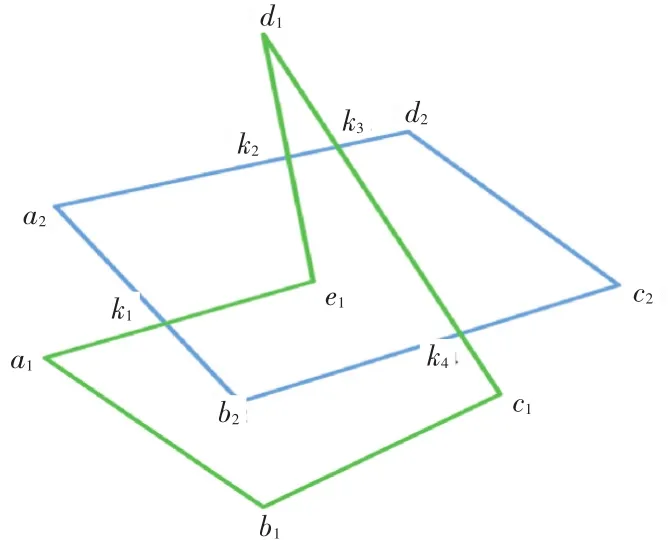
图2 两多边形交集

3.1 图形预处理

本文交集区域折线段的求取采用两个多边形互相遍历边的方式。对于一般的多边形，每条边上的两个点关于另一个多边形存在以下四种关系。

1）起点和终点都在多边形外。如图2中的b1c1、c2d2、c1d1等；

2）起点在多边形外，终点在多边形内。如图2中的a2b2、d1f1等；

3）起点在多边形内，终点在多边形外。如图2中的f1a1、b2c2等；

4）起点和终点都在在多边形内。如图3中的g2h2、b2c2等。

图3 两多边形交集

上述四种位置关系，包含了所有边与另一个多边形的位置关系。然而这四种关系又可以细分为多种情况，容易造成复杂多边形计算不准确，主要原因是一条边与另一个多边形的交点个数大于1，理论上可以根据不同“关系”，设计由交点“奇偶位置”选出组成交集多边形折线段规则，这样需要对四种关系分别设计规则，造成算法显得冗长复杂，下面本文将给出一种简单高效的处理方法。

本文采用“图形预处理”的方法解决该问题，具体预处理方法如下：如果一条边与另一个多边形交点个数大于1，则在每两个相邻交点中点处添加一个“虚拟的顶点”。则图2经过预处理后两个多边形为a1b1c1v1d1f1和a2b2c2d2v2。图3经过预处理得到新的多边形分别为a1b1c1v1d1e1v3v4和a2b2c2d2e2v2f2g2h2i2。加入的虚拟顶点用vi表示。通过上述预处理得到新的多边形，保证每条边与另一个多边形交点个数最大为1。预处理后的交集区域如图4所示。

图4 预处理后交集区域

如图4所示，经过预处理的两个多边形，如果存在交集区域，那么其中一个多边形至少必有一个顶点在另一个多边形内部。判断两个多边形顶点的包含关系都需要互相判断一遍。

3.2 求取交集折线段

经过预处理后，再来讨论前文中的四种关系。1）起点和终点都在多边形外。该线段全在多边形外，不做处理。

2）起点在多边形外，终点在多边形内。这种关系表示遍历方向从多边形外进入多边形内，生成一条新的“折线段”保存后续值。

3）起点在多边形内，终点在多边形外。这种关系表示遍历方向从多边形内走出到多边形外，结束一条“折线段”的记录。

4）起点和终点都在多边形内。该条边在多边形内，将起点和终点加入已经存在的折线段中。

求取图形折线段过程如下。

输入：经预处理后的平面二维点表示的两个多边形区域Q1，Q2。

1）按照某个顺序依次遍历多边形Q1中的每个顶点v；

2）以v点为终点，v点的前一顶点为起点，判断起点和终点是否在多边形Q2中。

3）参考上述四种关系。如果起点在Q2外，终点在Q2外，该线段全在Q2外，不做处理；如果起点在Q2外，终点在Q2内，遍历方向从多边形外进入多边形内，生成一条新的“折线段”，依次保存“进入交点”和v点；如果起点在Q2内，终点在Q2外，遍历方向从多边形内穿到多边形外，依次保存v点和“穿出交点”，保存折线段，结束该条折线段；起点在多边形内，终点在多边形内，该条边在多边形内，将起点和终点加入已经存在的折线段中。

4）结束多边形Q1的顶点遍历；

5）采用类似方法，依次遍历Q2中的所有顶点，计算各折线段；

6）输出组成两个多边形的交集区域的所有折线段。

3.3 拼接交集折线段

在“求取交集折线段”部分已经计算出了组成交集区域的所有折线段，下一步就是将所有折线段内的点按照先后顺序拼接成一个多边形。

方法如下。

输入：由上面计算得到的多条待拼接折线段组成的集合。

1）从折线段集合中任意选取一条折线段作为初始“拼接交集折线段”，取该条折线段的一个端点为起点，则另一个端点为终点；

2）用“拼接交集折线段”的终点与集合中剩余折线段的起点和终点比较，如果与某条折线段的起点重合，则正向拼接；如果与某条折线段的终点重合，则反向拼接，形成新的“拼接交集折线段”；

3）判断“拼接交集折线段”的起点和终点是否相等，即判断拼接的多边形是否已经闭合，如果闭合，保存该多边形，转下一步；否则，转2）；

4）判断集合是否为空，即所有的折线段是否都已经拼接，如果为空，转下一步；如果不为空，转1）继续新的多边形拼接；

5）输出所有拼接完成的多边形。

至此完成了两个多边形交集区域的算法设计。当残骸落区多边形确定之后，只需要将规避区域多边形与其进行上述计算即可。当规避区域是多个时，只需将每一个多边形与其计算即可［9］。

4 残骸落区和规避重合区域概率计算

利用计算机计算二维正态分布的概率涉及到复杂的二重积分计算，而且随着计算区域的复杂多变，这种积分计算更加复杂耗时［10］。积分计算的一个优点是精度非常高，然而大多数情况我们并不关心小数点第四位后的情况，因此本文采用一种近似的计算方法［11～12］，满足精度要求的同时使得算法更加简单，计算速度更快。

4.1 二维正态分布密度公式

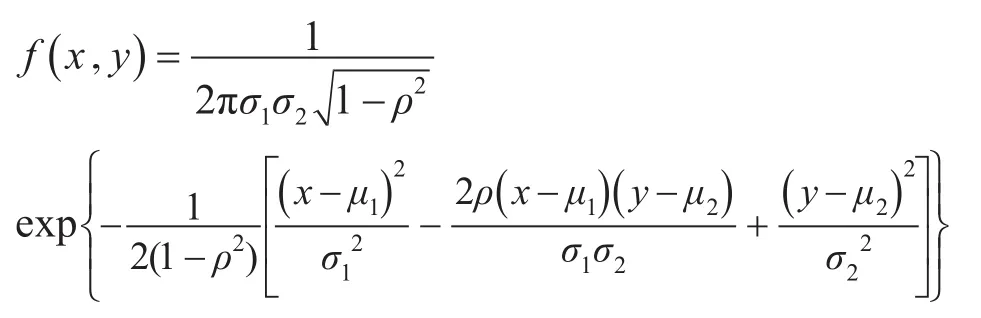
4.2 二维正态分布概率计算

对二重积分区域D内的概率为

本文采用的近似计算方法采用上述的思想，设想将积分区域D细分成无数个小网格，每个小网格的面积为gridArea，在每个小网格内选择一个特征点，计算该特征点对应的概率密度f(xi，yi)，则小网格对应概率Pgrid≈gridArea·f(xi，yi) ，小网格面积gridArea相当于长方体的底面积，f(xi，yi)相当于长方体的高，只要网格分得足够细，有。上述方法的理论基础是将做二元级数展开后，只考虑低阶项，忽略高阶项。

下面将详细讨论本文采用的近似方法，设μ1=0，σ12=1，μ2=0，σ22=1，ρ=0为标准二维正态分布，密度计算公式为fs(x，y)。参考图5，计算的步骤如下。

输入：残骸落区多边形区域C、残骸落区与边区域的交集多边形区域D

1）根据输入的残骸落区多边形C求解其在X轴和Y轴上的最大最小值，建立一个最小外包矩形M，左下点为(xmin，ymin)，右上点为 (xmax，ymax)。

3）建立到标准分布的转换方程，将上述平面上的值转换到标准二维正态分布中得：

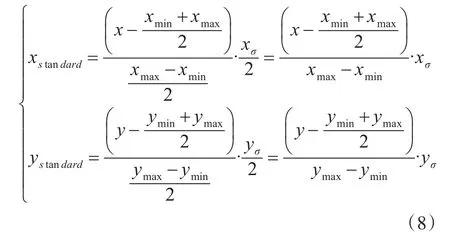
对于标准分布，由于σ=1，所以上式最后的σ都略去。上式使得xmin对应，xmax对应；ymin对应，ymax对应。对于原平面二维坐标系内的任意一点都可以转换到标准二维正态分布坐标系。

4）将最小外包矩形M在X轴和Y轴方向上分别N等分，于是共有N×N个方格，每个方格的，面积为dxdy；在标准二维正态坐标系中，。

5）取每个方格的中点(xci，yci)为该方格的特征点，将其转换到标准坐标系下：(xci_standard，yci_standard) ，如果该中点(xci，yci) 在在积分区域D内（并非残骸落区C，而是残骸落区与规避区域所有的交集区域为积分区域D），计算该方格区域的概率为fs(xci_standard，yci_standard)dxstandarddystandard。

6）叠加所有计算的方格概率，即为积分区域D的概率。同理，如果将积分区域D划分为若干个小区域Di，则可以按上述方法计算出每个区域Di的概率。

至此，完成关于导弹残骸落区和相应规避区域重合区域的二维正态分布的概率计算。

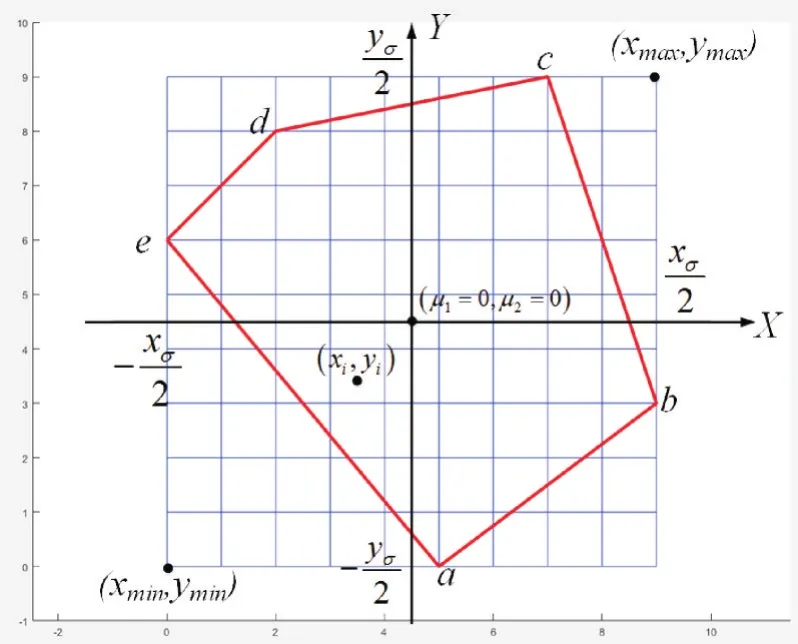
图5 平面二维系和标准二维正态分布坐标系

5 算例分析

程序执行环境为MatlabR2014a，设计安全阈值为book=68,ebook=73。以经度122，纬度26为导弹残骸落区分布中心，协方差矩阵为，随机生成一组导弹残骸落区二维高斯分布经纬度坐标点，随机生成规避区域的有序顶点经纬度坐标，使得规避区域在残骸落区内外都有分布，仿真结果如图6所示；通过上述坐标转换和地球投影方法较快算出了残骸落区多边形C和各规避区域多边形Gi在投影平面上的二维坐标，而后快速判断交集区域范围Ai，取N=1000，仿真结果如图7所示；并在构建的二维正态分布模型中定量快速计算残骸落区多边形和规避区域多边形的交集区域概率Pi，仿真分布图如图8所示，最终计算结果如表1所示。

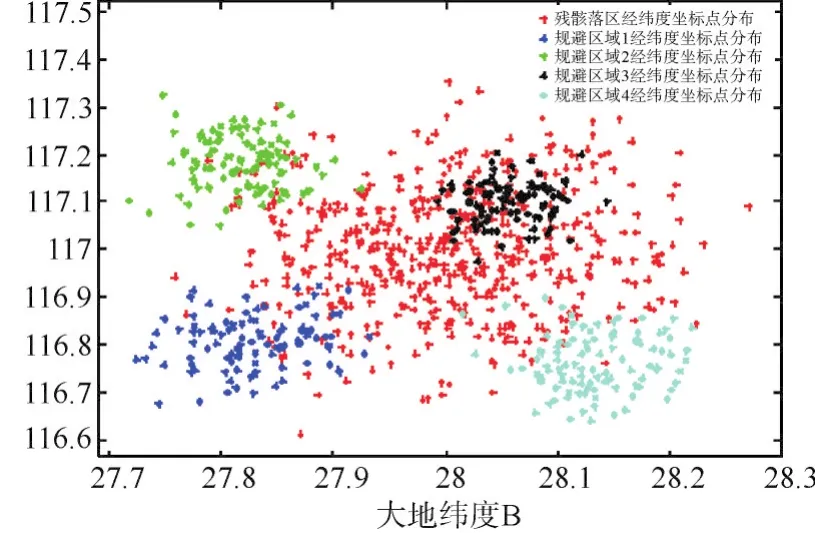
图6 残骸落区和各规避区域经纬度分布

图7 残骸落区和各规避区域在平面二维系分布

图8 残骸落区在平面二维系下标准正态分布

表1 交集区域计算概率

通过上述算例计算结果可知，规避区域G3对应的交集区域A3的概率要大于阈值Y，即导弹残骸落入该规避交集区域概率较大，因此，为安全起见，需要对该区域的人员物资进行转移；同理，因导弹残骸落入剩下规避区域概率极小，低于设定阈值，即该规避区域交集区域是安全的，相应区域人员物资则无需转移。相比较传统的转移全部规避区域人员物资而言，本文提出的算法不仅能够快速定量评估出残骸落区安全性，还极大地减小了实际过程中的转移工作量。

6 结语

本文对导弹残骸落区范围和地面规避区域交集区域安全性进行了研究。首先，推导了地球投影变换的相关算法过程，建立了从地理坐标系到切平面二维坐标系的转化过程。在此基础上，提出了一种判断确定两多边形交集区域范围的算法，快速计算确定了相应残骸落区和规避区域在二维坐标系上的交集区域。最后，通过构建二维正态分布模型定量快速计算导弹残骸落区多边形和规避区域多边形的交集区域概率，并将交集区域概率与设置阈值比较。算例结果显示，该算法易于实现，计算精度较高。当作战导弹数量多的情况下，该方法具有重要的工程应用价值。