基于稀疏堆叠自编码器和Circle Loss 的电机故障诊断

王玉龙，于凯，王哲，范尊正，陆慧

（安徽华电宿州发电有限公司，安徽 宿州 234000）

电机在工业生产中起着重要作用，然而，由于其常运行于复杂环境中，极易发生故障，严重影响企业的生产。电机故障诊断不仅能提高电机的安全性，同时，也能降低维护成本，对提高企业的整体经济效益具有重大意义。

传统的电机故障诊断方法，如K 最近邻算法、支持向量机（SVM）和人工神经网络（ANN），其主要步骤为故障特征提取和故障分类，但这些方法高度依赖专家知识，诊断准确性不高。另外，不同工况下电机故障特征也不同，上述方法在恒定转速下效果良好，但对于可变转速情况效率则大大降低。

目前，深度学习由于其强大的特征提取能力，能进行无监督的特征学习和分层特征提取，已成为解决计算机视觉和自然语言处理问题的有力工具，其不仅提高了各领域的分类问题的性能，而且还降低了特征提取和选择过程的复杂性。

本文利用深度学习的数据驱动思想，提出了一种转速波动下快速高效的电机故障诊断方法。首先，计算输入转速加速度信号的频率特征分布。在此基础上，将复包络谱作为稀疏堆叠自编码器（SSAE）的输入，并在SSAE 输出端通过Circle Loss 进行故障分类。为验证所提诊断方法的泛化能力，设计了最佳的网络结构，同时，对来自四个不同转速下故障数据进行了测试。结果表明，所提方法诊断准确性高，复杂度低，对转速恒定和波动均具有很好的适应性，能够对转速波动电机进行有效故障诊断。

1 复包络谱计算

复包络谱由实信号经过希尔伯特变换生成，对于时域信号x(t) ，对其进行希尔伯特变换得到解析信号a(t) ，其形式为。

2 稀疏堆叠自编码器（SSAE）

堆叠自编码器是由多个自编码器堆叠而成，其将输入x(t) 映射到隐空间表示，即：

其中，f1,W,b为编码器的激活函数、权重和偏置。

解码器通过从低维空间中重建输入，即：

式中，f2,W,′b′为解码器的激活函数、权重和偏置。

但堆叠自编码器泛化差，不适合转速波动故障，故本文通过加入稀疏约束，形成SSAE，降低训过拟合问题，并提高SAE 网络的泛化性能，网络的稀疏性通过在SAE 损失函数中引入正则项控制，即：

式中，稀疏正则项由KL 散度定义。

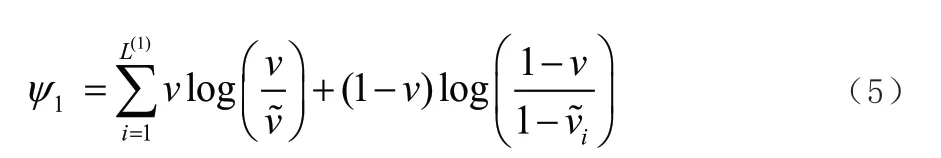
式中，为第i层经过激活函数后的输出。

3 Circle 损失

深度特征学习通常最大化类内相似度sp和最小化类间相似度sn，但sp和sn上的梯度的值总是一样的，这降低了特征空间的可分性。故本文把所有的sp和sn两两相减得到以下的Circle 损失函数。

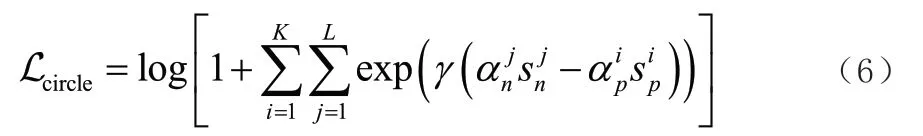
定义sp的最优值为Op，sn的最优值为nO，且np O

个相似性得分与最优值偏离较远，Circle Loss 将分配较大的权重，从而对它进行强烈的优化更新。为此，本文权重调整方式如下。

4 SSAE 网络训练流程

综上所述，SSAE 训练步骤如下：

（1）采用Xavier 方法初始化网络权重和偏置；

（2）输入样本x，并计算相应的激活值；

（3）计算网络每层输出和前馈量；

（4）计算Circle Loss；

（5）通过Circle Loss 反向传播更新权重；

（6）更新Circle Loss 数的梯度；

（7）重复以上步骤直至网络收敛。

5 仿真验证

本节使用宿州电厂电机的故障数据测试所提方法的有效性。分别在电机的外部，内部和转轴设置不同故障，收集对应的转速加速度，采样率为12kHz，故障直径为0.1778mm，裂纹深度为0.27cm。

设置1722、1748、1772 三种转速，形成四个数据集，分别包括正常、内圈、外圈和转轴等468 个故障样本。使用来自一个转速数据训练网络，其他转速数据进行验证。

5.1 SSAE 的网络结构设计

5.1.1 权重稀疏占比

研究发现，稀疏性保持在0.15 ～0.2 时，重构误差几乎不变。因此，本文的稀疏率值为0.15。

5.1.2 隐藏层数

研究对比可知，当SSAE 使用4 个隐藏层时，重构误差最小。此外，随着隐藏层数量的增加，重建误差并无明显下降。

综上，本文的网络结构如表1 所示。

表1 故障诊断网络结构

5.2 仿真结果

为进一步地说明所提方法故障诊断效果，本文对比振动频谱成像（VSI）、BP 网络以及本文方法的诊断精度，其结果如表2 所示。

表2 不同故障诊断方法精度

VSI 方法基于振动频谱成像和人工神经网络的轴承故障诊断，首先，对振动信号进行快速傅立叶变换，将频谱进行叠加创建灰度图像，经过8×4 大小的滤波器后，利用阈值法转换为二进制图像，ANN 的输入即为该二进制图像。

从表2 可以看出，本文方法的平均故障分类精度均在90%以上。而VSI 和BP 两种方法尽管在恒定速度情况具有较好的诊断性能，但在当速度波动后诊断性能明显下降。可见，本文方法能有效提取故障的复包络谱和故障特征频率特征，从而提高了故障诊断精度。

6 结语

本文提出了一种转速波动下快速高效的电机故障诊断方法。首先，计算得到输入转速加速度信号的复包络，并将其作为SSAE 的输入，并通过Circle Loss 函数进行故障分类。为验证所提方法的泛化能力，本文进行了一系列的对比试验，设计了最佳的网络结构，同时，对来四个不同转速下故障数据进行了测试。结果表明，本文所提方法复杂度降低，泛化能力好，对转速恒定和波动均具有很好的适应性。