货物三维装箱问题建模及其乌鸦搜索算法优化
王素欣 温恒 卢福强 刘浩伯 王雷震


摘 要:针对货物三维装箱问题建立三维装箱模型. 在模型中,为避免货物在运输过程中转弯时由于偏心导致翻车现象的发生,加入了考虑转弯时重心约束,得到重心区域投影为等腰三角形或者等腰梯形. 货物放置规则中扩大了剩余空间区域,增加了解的多样性. 在算法中,为了提高迭代收敛速度,增强其全局寻优的能力,采用改进的乌鸦搜索算法对模型进行求解与优化. 在改进算法中,提出并引入了多概率随机游走策略和解修复策略. 解修复策略使得算法适用于模型求解,尽可能增加解的多样性. 多概率随机游走策略是种群迭代后继续以多种不同的概率进行随机游走,使得算法全局寻优能力更强. 仿真实例与基准函数测试结果表明,改进后的算法优化效果明显.
关键词:三维装箱问题;集装箱装载问题;乌鸦搜索算法;转弯重心约束;集装箱包装公司;优化与决策
中图分类号:TP391 文献标志码:A 文章编号:1674—2974(2020)08—0021—10
Abstract:Aiming at the three-dimensional bin loading problem of cargo, a three-dimensional cargo loading model is established. In the model, in order to avoid the phenomenon of rolling over due to the eccentricity during the turn of the goods in the process of transportation, the gravity center constraint during the turn was added to obtain the projection of the gravity center area as an isosceles triangle or isosceles trapezoid. The cargo placement rules expand the remaining space area and increase the diversity of understanding. In order to improve the speed of iterative convergence and enhance its global optimization ability, an improved crow search algorithm is adopted to solve and optimize the model. In the improved algorithm, a multi-probability random walk strategy and a reconciliation strategy are proposed and introduced. The solution repair strategy makes the algorithm suitable for model solving and increases the diversity of solutions as much as possible. The multi-probability random walk strategy is to continue to walk randomly with different probabilities after population iteration, which makes the global optimization ability of the algorithm stronger. Simulation examples and benchmark function test results show that the improved algorithm has obvious optimization effect.
Key words:three-dimensional bin packing problem;container loading problem;crow search algorithm;center of gravity constraint in turning;container packaging corp;optimizaton and decision
货物装箱与物流运输过程影响着企业的竞争力、成本、客户满意度、销量、以及市场占有率,直接影响着企业的盈亏情况甚至是企业未来的发展. 货物三维装箱问题的优化,可以减少物流过程所需要的成本,提高物流运输效率,使企业得到更好发展.
货物三维装箱问题其本质属于装箱问题(Bin Packing Problem,BPP). 作为一个经典的组合优化问题,“组合爆炸”现象的出现,导致这个NP-hard问题的最优解很难找到.
目前,装箱问题应用广泛,考慮平衡、稳定等因素的货物三维装箱问题逐渐增多. Galr?觔o等[1]针对集装箱装载问题,提出了一种具有静力稳定约束的集装箱装载算法,指出了静态稳定性与动态稳定性的对立关系. Martínez等[2]考虑动态稳定约束的集装箱装载问题,提出了坠落箱数及加速时可能损坏箱数两项动态稳定性指标. 装箱问题的求解方法可以粗略地分为运筹学方法和启发式方法两大类. Paquay等[3]针对三维多尺寸箱型的装箱问题,考虑了箱子的易碎性、稳定性和定位,以及箱子的特殊形状和重量等因素,提出了一个快速的建设性两阶段启发式算法. Alonso等[4]考虑了几何、重量、重心、动力稳定性等约束,采用整数线性模型解决了多集装箱装载问题.
现有三维装箱研究中存在如下问题:
1)一些模型的约束条件不完善,重心约束没有考虑转弯情况.
2)目标函数考虑较少,部分模型未说明假设条件.
3)用到的遗传算法等求解方法较旧,全局寻优的能力较弱,迭代收敛速度较慢.
乌鸦搜索算法[5](Crow Search Algorithm,CSA)自被提出以来,广泛应用到诸多领域,如图像分割[6]、数据挖掘分类问题[7]、帕金森病的诊断[8]、评估噪声对损伤检测过程的影响[9]、图像处理问题[10]等. 改进乌鸦搜索算法的方法可以分为两大类,一类是引入策略对算法进行改进. 例如,Sayed等[11]引入了10种混沌映射,提出CCSA;另一类是与其他算法相结合的混合算法. 例如,Javaid等[12]将CSA与蝙蝠算法混合,提出了BCSA. Pasandideh等[13]将CSA和正弦余弦算法的优点相结合,提出了余弦乌鸦搜索算法.
针对上述问题,为了减少翻车情况的发生,建立了具有考虑转弯情况、重心约束等7个约束条件,容积利用率、载重总重量、重心坐标等5个目标函数的多约束多目标货物三维装箱模型. 为了使乌鸦搜索算法更好地适配装箱问题,同时加快迭代收敛速度,提高全局搜索能力,提出并引入了多概率随机游走策略和解修复策略对原始乌鸦搜索算法进行改进,并对模型进行了求解,装箱效果更好.
为了验证改进CSA的有效性,結合实例通过遗传算法、粒子群算法、乌鸦搜索算法、灰狼优化算法[14](Grey Wolf Optimizer,GWO)、鲸鱼优化算法[15](Whale Optimization Algorithm,WOA)、最有价值球员算法[16](Most Valuable Player Algorithm,MVPA),以及改进后的乌鸦搜索算法对货物三维装箱问题进行了优化仿真与测试,进一步说明了改进后的算法迭代收敛速度更快,跳出局部最优的能力更强. 为了说明改进后的算法在连续问题中的适用性,通过对3个基准函数测试以及和其他部分算法对比,验证了改进后算法的优越性.
1 货物三维装箱模型的建立
由于大部分装箱问题研究中给出的重心约束都没有考虑货车转弯的情况,针对这一现象,建立了考虑转弯的情况的模型,并得出了与其他研究不一样的重心约束条件.
1.1 问题假设与符号说明
1.1.1 问题假设
由于货车的实际运输过程较为复杂,为了将问题简化,提出如下假设:
1)货车车厢与货物均为标准长方体结构.
2)所有货物均密度均匀,其质心为长方体结构几何中心,且不发生形变.
3)用泡沫或棉花填充空隙,忽略填充物重量.
4)装载时,货物的高必须与车厢的高平行.
5)运输过程中,货车转弯时的行驶路线为规则的圆形道路.
6)运输过程中,道路均为平坦的道路,若存在倾斜情况,倾斜角度始终不变.
1.1.2 符号说明
模型用到的符号及相关说明见表1.
对货物按照从1到D的顺序进行编号,设可行解的结构为:
式中:X的每一行表示一个解Xn;xnd∈[-D,D],且xnd是不为0的整数,表示第d个装入的货物其序号为xnd,xnd > 0表示货物的长与车厢的长平行,xnd < 0表示货物的长与车厢的宽平行.
1.2 建立货物三维装箱模型
在保证货物与货物之间不存在镶嵌、包含现象,且货车转弯过程中不翻车的条件下,将货物按照一定的顺序以及摆放方式装入到车厢内. 综合考虑容积利用率以及货物合重心等因素对整个装载运输过程的影响,对货物三维装箱问题建立合理的模型.
1.2.1 目标函数
下面对货物三维装箱问题建立具有优先级的多目标优化模型. 考虑到运输成本的因素,应当尽量减少货物运输的次数,因此,货物装箱的第1目标是车厢容积的利用率最大,即第1目标函数的表达式如式(2)所示. 合理利用空间之后,要合理利用载重量,在满足第1个目标的情况下,货物装箱的第2目标是装载货物的总质量最大,即第2目标函数的表达式如式(3)所示. 不倒翁之所以不倒,正是因为其重心低的缘故,物体的重心越低越稳定,因此,货物装箱的第3目标是在满足前2个目标的情况下,货物合重心的高度最低,即第3目标函数的表达式如式(4)所示. 货物装箱的第4目标是在满足前3个目标的情况下,货物合重心的Y坐标最靠近车厢宽度的中心,即第4目标函数的表达式如式(5)所示. 一般情况下,上述4个具有优先级的目标函数足以区分不同的解,为了使模型的适用情况更加广泛,这里引入第5目标,假设运输过程中要求在满足前4个目标的情况下,货物合重心的X坐标要最靠近车厢长度的中心,则第5目标函数的表达式如式(6)所示. 即在满足约束且货物容积利用率最大的情况下,进一步按优先级顺序对合重心的各个坐标进行建模与优化.
1.2.2 约束条件
在物流领域中,货物装箱后存在配送过程,转弯的时候由于货物偏心容易翻车. 为了避免翻车现象的出现,在货物装箱过程中加入考虑转弯的重心约束.
1)转弯时重心约束的推导过程
以(xi,yi,zi)表示第i个箱子的质心的坐标,则I个箱子的组合体质心坐标表示为(x,y,z),其公式如下:
考虑到货车转弯的对称性,对货车右转弯过程进行分析. 货车转弯时,相当于受到一个离心力的作用,此时,货车更容易绕着以货车左前轮、左后轮分别与地面接触的两点所确定的直线看作为转轴逆时针翻转. 以靠近车头的车厢左下角为原点,其引出的3条棱所在直线分别为X轴、Y轴、Z轴建立空间坐标系对车厢进行分析,仅考虑YOZ平面,即将车厢投影到YOZ平面上,对货车在即将翻转的临界状态进行受力分析,如图1所示.
左下角的转轴在YOZ平面投影为O点,其坐标为(0,0),货物重心在YOZ平面投影为C点,其坐标为(y,z),直线CO与车厢底边Y轴所夹的锐角为α:
同理,当道路存在倾斜角为β的情况时,考虑最糟糕的情况,可以得到此时如果想要避免翻车,需要满足约束条件,
式(15)所表示的重心约束条件是其他文章没有考虑的,加入此约束后,货物三维装箱问题更贴合实际情况,并且可以进一步降低货物运输过程存在的安全风险. 重心应该位于图3中的阴影区域.
2)约束条件描述
模型的约束条件描述为:
a)保证货物不悬空放置.
b)保证货物与货物之间不存在镶嵌、包含的现象.
c)货物总重量不能超过货车的载重量.
d)货物的总体积不能超过货车的总容积.
e)货物放置的顶面要与车厢顶面平行,货物放置的前面要与车厢前面平行.
f)装入的货物不能有在集装箱箱外的部分.
g)货物的组合重心满足式(15)约束条件.
3)约束条件的特点
上述约束中,前6个为常用的现实约束,约束条件g中重心约束范围与其他研究不同. 其他研究未考虑转弯情况,只在静止情况下得到的重心范围投影为矩形区域,约束条件g考虑了转弯情况,得到的是等腰三角形或等腰梯形區域,模型相对更完善.
1.2.3 货物放置规则与特点
1)放置规则
将空容器看作一个剩余空间,将货物的左后下角与剩余空间的左后下角重合放置货物. 放入的货物其每个面均可将占用的剩余空间切割为两部分,取货物不占用的那部分空间作为新的剩余空间. 图4表示货物上面切割出的剩余空间S.
每个面都切割空间后,删除容积为0的剩余空间,将得到剩余空间与已有的剩余空间合并. 得到新的剩余空间,并尝试放入下一个货物. 货物按照解序列所对应的货物编号依次放入容器,且优先放在靠下的剩余空间中.
2)放置特点
其他大部分文献中,上空间的分割得到的底面积和货物顶面的面积相同,即货物上面的货物,其底面面积必须不超过下方货物的顶面面积,相当于增加了限定,而这里的规则突破了限定,增加了解的多样性.
2 改进CSA求解货物三维装箱问题
对货物三维装箱模型优化求解的目的是为了得到一个更好的装箱方案,在保证运输安全的情况下,更好地利用装载空间,从而尽可能减少运输成本.
2.1 CSA求解货物三维装箱问题
乌鸦搜索算法(CSA)是Askarzadeh[5]在2016年提出的启发式算法. 其灵感来自于群居的乌鸦隐藏自己多余食物的过程. 乌鸦隐藏自己的食物,既要不被其他乌鸦发现,又想跟随其他乌鸦找到它隐藏的食物. 由于其相对较好的优化效果,被广泛应用在各个领域中.
随机初始化所有乌鸦种群X,如式(1).
初始化乌鸦的记忆E,作为当前每个乌鸦的历史最优位置,即每个可行解的历史最优解.
按照解序列进行货物装箱,计算式(2)~式(6)所描述的5个目标函数值,再进行下一步迭代,迭代更新出新的乌鸦种群,即新解,更新公式为:
式中:n表示当前第n只乌鸦;s表示第s只乌鸦且s≠n;Xtn与Xt+1n 分别表示在t时刻和t+1时刻乌鸦n的位置;Ets表示在t时刻乌鸦s的记忆;rn、rs为两个随机数且rn,rs∈[0,1];Ats表示t时刻乌鸦s的感知概率;ltn表示乌鸦n的飞行距离,ltn与Ats需要预先设定好.
检查新解是否可行,如果不可行,将它修正为可行解. 解的具体修正过程将在下文中进行详细介绍.
再次计算5个目标函数值,更新乌鸦记忆,即每个个体的历史最优解. 更新公式为:
继续迭代更新乌鸦种群,修正解,计算目标函数,更新记忆,如此循环,直到满足最大迭代次数或者其他终止准则时停止. 得出M中最优的解作为最终的最优解.
2.2 改进CSA的策略
由于原始CSA主要用于连续问题,且迭代收敛速度慢,容易陷入局部最优,因此,这里对CSA进行改进,提出了两个改进策略.
2.2.1 解修正策略
原始CSA主要用于求解连续函数的极值问题,属于连续问题,而货物三维装箱问题的解是离散的,直接用CSA求解并不符合实际情况,原始CSA并不适用. 为了将CSA与货物三维装箱问题适配,且尽可能增大解的多样性,这里提出了解修正策略,图5是解修正策略的一个例子.
为了保持解的符号不变,先将解的符号提取出来,正号记为1,负号记为-1,如果为0则视为正号. 再将解序列的绝对值按照从小到大进行排序,如果大小一样则保持其相对顺序,将排序后的序号与解的符号按位相乘对解进行重新编码.
2.2.2 多概率随机游走策略
在加入解修正策略之后,CSA与货物三维装箱问题成功匹配了,但是其迭代收敛速度还不够快,跳出局部最优的能力还不够强. 为了得到更优方案,引入多概率随机游走策略对乌鸦搜索算法进行改进,具体操作步骤如下.
式中:Xtn为第n只乌鸦在第t时刻随机游走前的位置;Xt,hn 为第n只乌鸦在第t时刻采用第h个概率随机游走方式游走后的位置,h = 1,2,3;■t为乌鸦种群X对每1列的元素计算平均数后得到的一个行向量;q4,q5,q6,q7,q8,q9∈[0,1],且为随机数;kth为t时刻第h个概率随机游走方式游走的步长,kt2的默认值为2,kt1、kt3的默认计算公式为:
游走之后,分别计算Xt,hn 的函数值,选出最优的一个,存入与之对应乌鸦的记忆中. 继续进行原算法的循环迭代操作.
2.2.3 改进CSA流程图
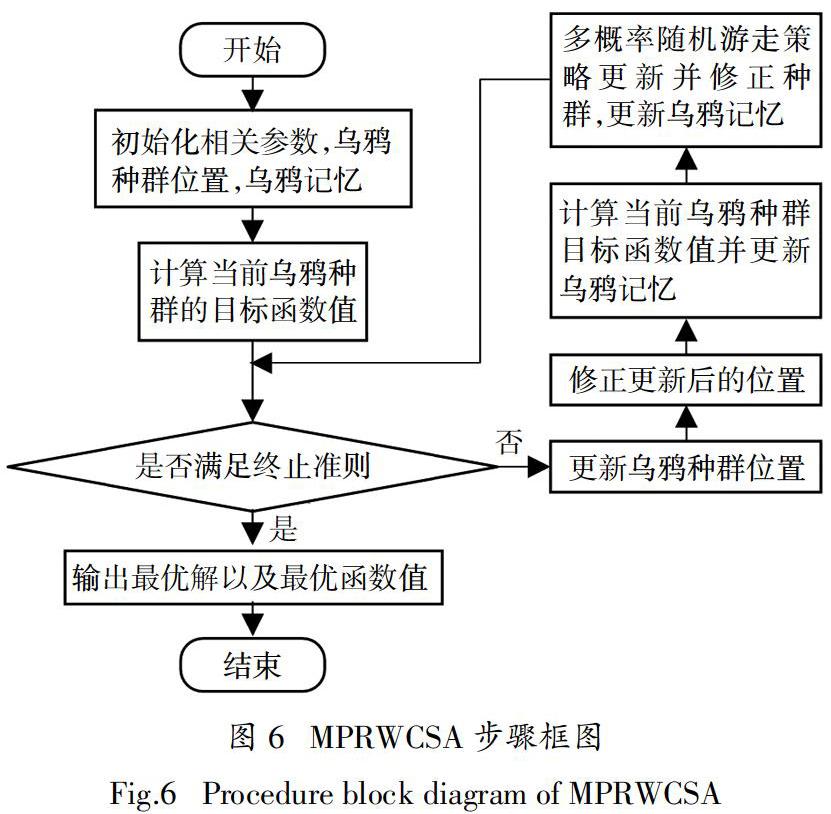
将改进后的CSA称为多概率随机游走乌鸦搜索算法(Multiple Probability Random Walk Crow Search Algorithm,MPRWCSA). MPRWCSA是在原始CSA的基礎上加入了解修正策略和多概率随机游走策略两个重要步骤,对于MPRWCSA,其算法步骤流程图如图6所示.
3 仿真实验及结果分析
3.1 装箱实例仿真
3.1.1 案例说明
设置转弯时最大行驶速度Vmax = 72 km/h,道路转弯的倾斜角β = 22°,转弯半径R = 0.1 km,重力加速度g = 9.8 m/s2.
货车车厢与货物的规格[17]分别见表2及表3.
设置种群数为150,最大迭代次数为1 000,分别用灰狼优化算法(GWO),鲸鱼优化算法(WOA),乌鸦搜索算法(CSA),最有价值球员算法(MVPA),遗传算法(GA),粒子群优化算法(PSO)以及MPRWCSA对该案例进行建模,借助MATLAB程序对问题进行求解.
3.1.2 仿真结果
计算每个算法模型求解10次后平均值,只分析每一代中第2目标函数(重心高度最低)的值,可以得到如图7所示的迭代收敛速度曲线.
通过仿真实验可以得到,货物装箱的最大体积为17 816.336 m3,最大装载质量为17 682 kg,最大容积利用率为60.095 8 %,最优解的质心坐标为(2 407.425 2,1 147.815 7,663.556 16),最优解序列为3,11,-2,15,-8,6,5,-16,-1,9,4,14,10,12,-13,7,装箱效果图如图8和图9所示,仿真结果见表4.
3.1.3 结果分析
通过图7可以直观地看出,改进后的乌鸦搜索算法(MPRWCSA)迭代效果明显优于其他优化算法,迭代收敛速度更快,得到的解更优. 表4中,从解的优劣程度上可以看出,CSA、WOA、 MPRWCSA所得到的解,明显优于GWO、MVPA、GA、PSO. MPRWCSA的合重心Z轴坐标的平均值较其他算法更优,10次实验中,Z轴坐标的最优值比GWO、MVPA、GA、PSO好,虽然与WOA、CSA相同,但在Y轴坐标的最优值上效果更好. 相比较CSA与WOA,MPRWCSA达到最优解时所需要的平均迭代次数小于CSA与WOA. 说明改进CSA后得到的MPRWCSA其迭代收敛速度更快,跳出局部最优的能力更强,在离散问题的应用上效果较好.
文献[8]和文献[19]中也用到了相同的仿真案例,对比实验结果发现,MPRWCSA得到的结果在重心上优于文献[17-19]中的结果,且模型更为合理.MPRWCSA由于其在更新后,还会按照不同的概率继续随机游走,结合解修复策略,因此比其他算法优化效果相对较好.
3.2 基准函数测试仿真
3.2.1 案例说明
通过3个常用的基准函数(Ackley、Sphere、Rastrigin)对MPRWCSA进行测试,并与CSA、PSO、GWO、WOA进行对比. 其中,Sphere函数为单峰函数,Ackley函数虽是多峰函数,但是峰值间差距不明显,Rastrigin函数是显著的多峰函数. 3个基准函数的表达式及其对应自变量的取值范围见表5. 问题维度设为2时,函数的图像如图10所示.
设置种群大小为150,最大迭代次数为1 000,问题维度为30,分别对MPRWCSA和CSA进行30次测试.
3.2.2 仿真结果
依次将不同基准函数的30次测试历代当前最优值取平均值,绘制迭代收敛的半对数曲线,如图11~图13所示. 记录30次测试的最优解,根据这30个数据,计算出最优值、最差值、平均值、标准差、平均时间等评价指标,结果见表6.
3.2.3 结果分析
通过图11~图13可以看出,MPRWCSA能够很好地应用在连续问题中,且其前期的迭代收敛速度明显优于其他几个算法. 从最终结果上看,除Ackley函数中不及GWO外,MPRWCSA得到的结果相对更优一些. 从表6中可以看出,较CSA而言,除运行时间与Ackley函数中测试标准差外,其他各项都比后者更优. 较WOA而言,除Ackley函数中测试最优值外,其他各项都比后者更优. 较PSO与GWO而言,
虽然最优值和运行时间上结果比后者差一点,但其算法稳定性较好. 改进后的算法主要是为了提高前期的迭代收敛速度与全局搜索的能力,对于连续问题的寻优精度改进效果并不明显.
图11中,MPRWCSA得到的结果其精度不如GWO的原因是由于CSA结果的精度比GWO差,而MPRWCSA并未针对最优解精度进行改进,主要改进了迭代收敛速度与全局搜索能力.
4 结 论
针对货物三维装箱问题进行了建模与优化,提出了更完善的模型与更高效的求解方法.
1)模型上的改进. 在6个现实约束的基础上,加入了考虑转弯时的重心约束,建立了容积利用率、载重总重量、重心坐标等5个目标函数的货物三维装箱优化模型. 其中,重心区域的投影为等腰三角形或等腰梯形,较其他文献中的矩形区域而言,考虑得更全面.
[12] JAVAID P N,MOHSIN S M,IQBAL A,et al. A hybrid bat-crow search algorithm based home energy management in smart grid[C]// Barolli. Complex,Intelligent, and Software Intensive Systems. Torino. Italy:Advances in Intelligent Systems and Computing,2018: 75—88.
[13] PASANDIDEH S H R,KHALILPOURAZARI S. Sine-cosine crow search algorithm: theory and applications [J]. Neural Computing and Applications,2020,32:7725—7742.
[14] MIRJALILI S,MIRJALILI S M,LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software,2014,69:46—61.
[15] MIRJALILI S,LEWIS A. The whale optimization algorithm [J]. Advances in Engineering Software,2016,95:51—67.
[16] BOUCHEKARA H R E H. Most valuable player algorithm:a novel optimization algorithm inspired from sport[J]. Operational Research,2017,80:1—57.
[17] 卜雷,袁新江,蒲云,等. 基于遗传算法的集装箱单箱三维装载优化问题[J] .中国铁道科学,2004,25(4):108—111.
BU L,YUAN X J,PU Y,et al. Three- dimensional loading optimization problem of container single box based on genetic algorithm [J]. China Railway Science,2004,25(4):108—111. (In Chinese)
[18] 朱莹. 基于混合遗传算法的集装箱船三维装箱问题研究[D]. 武汉:华中科技大学船舶与海洋工程学院,2016:50—52.
ZHU Y. Container ship three-dimensional loading problem based on hybrid genetic algorithm[D]. Wuhan:School of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,2016:50—52. (In Chinese)
[19] 崔會芬,许佳瑜,朱鸿国,等. 基于改进遗传算法的三维单箱装箱问题研究[J]. 工业工程与管理,2018,23(1):86—89.
CUI H F,XU J Y,ZHU H G,et al. Study on three dimensional single boxpacking based on improved genetic algorithm [J]. Industrial Engineering and Management,2018,23(1):86—89. (In Chinese)

