考虑风电机组电压均衡性的风电场无功优化策略

张建委，蔺 红

(新疆大学电气工程学院，新疆 乌鲁木齐 830047)

0 引 言

风力发电本身具有随机性、波动性[1-2]，大规模风电并入电网后给电网带来诸多的不利影响，其中以并入电网后无功电压的调控问题尤为突出[3- 4]。鉴于此，国内外学者对双馈风电场电压控制问题做了大量研究。文献[5- 6]通过协调控制双馈风电机组和无功补偿装置(STATCOM)的无功功率分配，完成双馈风电机组低压穿越的机端电压恢复速度。文献[7]通过对风电场集电系统的无功电压灵敏度和网损灵敏度的分析，按照灵敏度系数对无功补偿装置和双馈风电机组分配无功量。文献[8]分析风电场各支路节点的电压偏差确定无功出力风机的数量，并优先选择离风电场联结点最近的风机作为无功出力源。文献[9]提出以均衡风电机组机端电压裕度、提高无功补偿设备容量和提高系统电压稳定性为目标的控制策略。文献[10]分析了风电机组的无功出力特性，但在未考虑风电场内馈线的情况下给风电机组分配无功出力量，在某些外部扰动的情况下很可能造成场内某些机组电压越限脱网。上述研究多以风电场并网点电压为控制目标，并未同时以并网点电压和机端电压为控制目标，由于风电机组对电压比较敏感，极易受到电压波动的影响造成脱网。

本文在分析双馈风电场拓扑结构的无功电压特性基础上，提出了一种同时以风电场并网点电压和机端电压偏差最小为目标的无功优化策略，通过详细分析风电场内馈线对机组机端电压的影响，利用网络分析法非迭代计算求取风电机组端电压的无功出力上下限，最后采用PSO算法对风电场内的风电机组、无功补偿设备进行合理的无功分配，在稳定并网点电压的同时减小机组机端电压之间的偏差，提高风电并网系统整体的电压水平。

1 风电场内馈线电压—无功分布特性

风电场通常采用低压母线为单母线或单母分段，每段母线上连接若干条馈线，每条馈线上接多台机组，接线方式如图1所示。

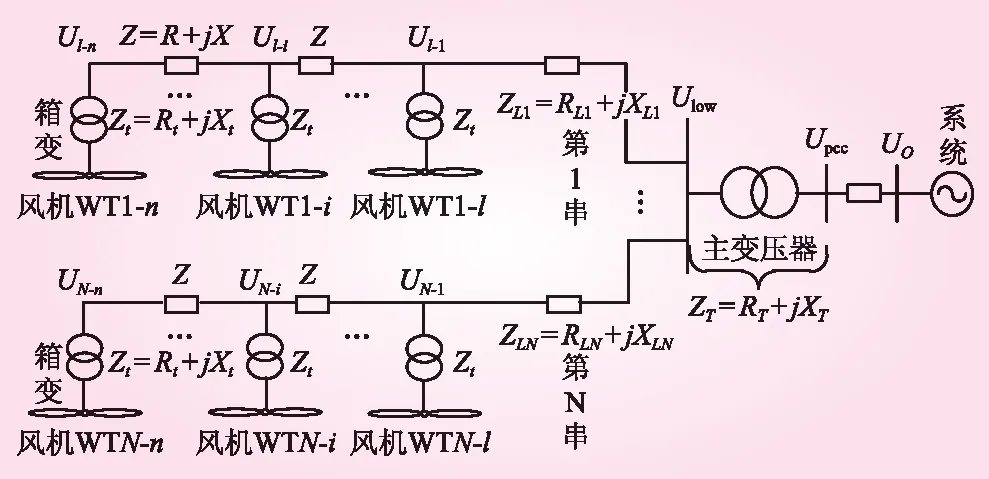
图1 风电场的典型接线示意

设风电场内有N条馈线，每条馈线上接有n个风电机组，相邻风电机组之间的线路阻抗Z(各机组之间的等距离连接)，Zt=Rt+Xt为风机箱式变压器阻抗；Rt、Xt分别为箱变的电阻和电抗；ZLi=RLi+XLi为第j条馈线上第一台机组到升压站低压侧母线ULOW的线路阻抗；RLi、XLi分别为第j条馈线上第一台机组到升压站低压侧母线的电阻和电抗；ZT=RT+jXT为风电场升压变压器的阻抗；RT、XT分别为主变压器的电阻和电抗；Uj-i(j=1，…，N;i=1，…，n)为第j串第i台机组箱变高压侧的电压；Upcc为风电场并网点电压；Pj-i、Qj-i(j=1，…，N;i=1，…，n)分别为第j条第i台机组的有功和无功出力。

风电场主变低压侧的电压ULOW为

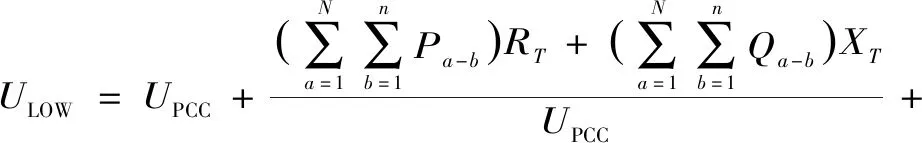
(1)

鉴于风电场主变低压侧电压ULOW为风电场集电线路电压等级为10 kV的较短线路，可忽略网损及电压降落横分量，得机组箱式变压器高压侧的电压Uj-i为

(2)

式(2)第二部分是第j条ZLj上的压降；第三部分是第j条馈线第一台机组到第i台机组集电线路间的电压降。由式(2)得各机组机端电压为

(3)

由式(1)～(3)得，首先风电机组的电压水平由风电场PCC母线电压决定，当风电场PCC母线电压发生波动时，机组的机端电压也会随之变化发生。此外，由于风速的不确定发性，机组的输出功率也会发生波动，造成机组的机端电压产生偏移，由于等电场内的机组相互关联，风电场内的某一台机组输出功率发生变化，特别是无功发生时，对整个风电场内的其他机组也会产生影响，根据式(1)～(3)得机端电压与机组之间风机无功出力的关系为：

(4)

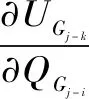
2 风电场无功电压优化控制策略

本文所提的风电机组电压均衡性的风电场无功优化策略如图2所示，图中UPCC为风电场并网点实际电压；UPCC-ref为风电场并网点参考电压；UGj-i-ref为风电场双馈风电机组的参考电压；QSVC为SVC无功控制信号；QGj-i-ref为双馈机组的无功参考信号。

图2 控制策略结构示意

双馈风电场以在线实时监控数据为基础，根据并网点电压的波动情况计算风电场所需的无功功率及风电机组此刻的无功调整量，最后按无功分配原则给风电机组和无功补偿设备下达控制信号。图2中电场PCC点经过主变压器到风电场低压母线所需的无功率Q为

(5)

式中，X为风电场到风电场低压母线的等值阻抗。

由式(2)、(3)得，风电机组到风电场低压母线所需的无功为

(6)

式中，(Xt+Xj-i)为第j条馈线第i台风机箱变低压侧到风电场低压母线之间的等值电抗。

本文所提的无功控制思想是：在满足并网点电压的前提下，尽可能的减小机组的机端电压偏差，改善机组电压的运行稳定性。具体的控制策略流程如图3所示。

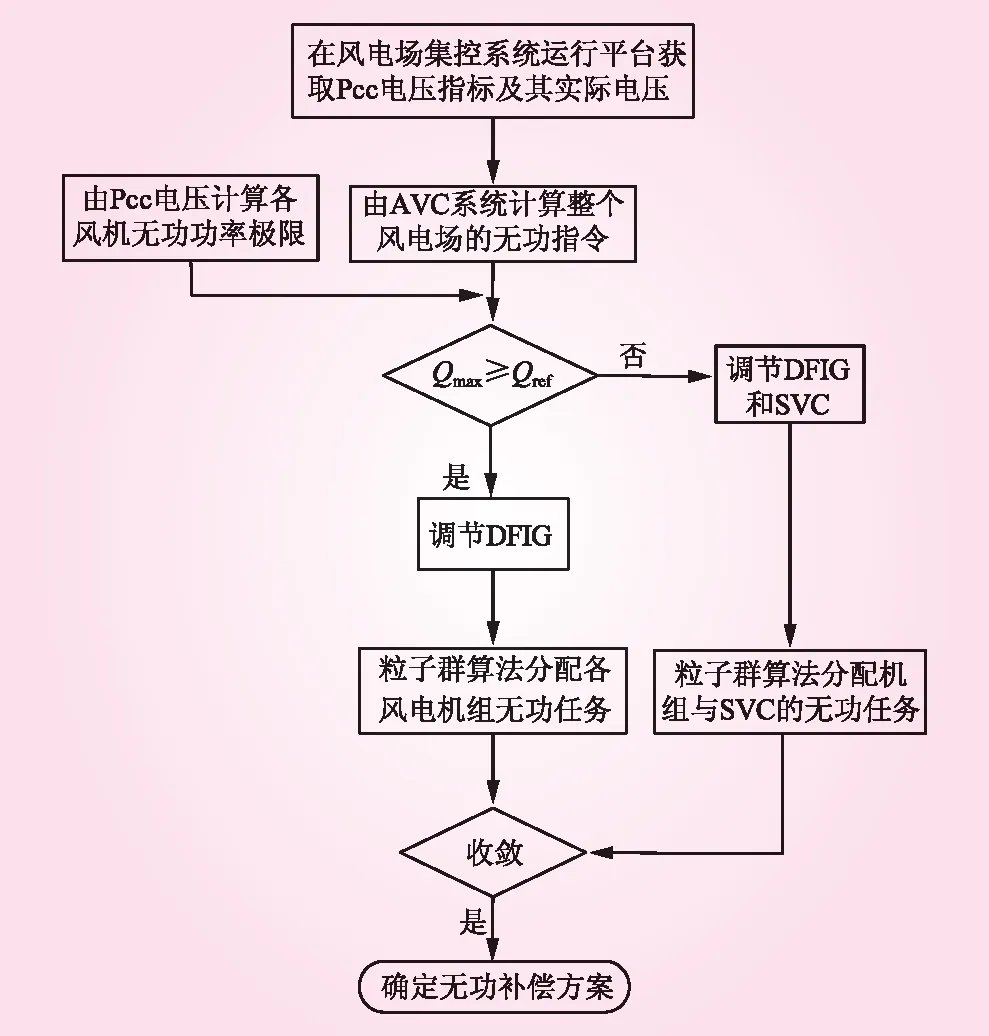
图3 控制策略流程示意

3 风电场无功优化数学模型

本文所提的双馈风电场无功控制策略的控制变量是风电场风电机组的无功出力，因变量为并网点电压和机组的机端电压。

3.1 目标函数

提高并网点电压的稳定性是风电并网的首要目标

F1=min(UPCC-UPCC-ref)2

(7)

式中，UPCC、UPCC-ref分别为并网点电压的测量值和参考值，取UPCC-ref=1.00(p.u.)。

以机组机端电压偏差最小为目标

(8)

式中，UGj-i、UGj-i-ref分为风电机组的机端的实测电压和参考值；机端电压偏差为ΔUGj-i=(UGj-i-ref-UGj-i)，取UGj-i-ref=1.02(p.u.)。

综上，以并网点电压最优，风电机组机端电压偏差最小，动态无功容量储备充裕为目标的本文控制策略总的目标函数为

F=λ1F1+λ2F2

(9)

式中，λ1、λ2为各目标函数中的权重系数。

3.2 约束条件

潮流约束条件

(10)

式中，Ni为节点总数；Pi、Qi分别为节点i注入的有功和无功；Gij、Bij分别为节点i和节点j间的电导电纳；θij为节点i和j间的电压相位差。

变量约束条件

(11)

4 模型求解

PSO算法具有易于理解、计算精度准确性高、收敛快等优点[11-12]，在优化计算中广泛应用，鉴此本文采用该算法对所建立的模型求解，求解步骤如下：

(1)在风电场监控平台上实时获取PCC电压、风电机组机端电压及变化情况。

(2)给出约束条件的上下限。

(3)给定粒子群的规模以及惯性权重系数等相关参数，随机初始化种群产生N个可行解。

(4)把各个粒子代入目标函数，再次潮流约束方程计算，求得初始化粒子的适应度值，选定当前粒子位置为个体最优解pbest，gbest为目前种群最优解。

(5)对各个粒子的速度和位置更新，检查是否达到终止条件(最大迭代次数)，满足则停止，否则返回步骤4。

5 算例分析

本文参照新疆某实际风电场在仿真软件MTLAB/Simulink上搭建模型，该风电场由33台1.5 MV的双馈风力发电机组成，总装机容量49.5 MV，风电场分为3条馈线，每条馈线接11台机组，每台机组的箱变为690/35 kV，风机间距为600 m，集电线路型号为LGJ-185。升压站低压母线装有20 MV·A，的动态补偿装置SVC。通过一台容量为50 MW的220 kV的主变压器经长为35 km的送电线路与电网直接相连，如图4所示。

图4 仿真系统结构示意

本文采用PSO算法确定风电机组和无功补偿装置的无功量值，算法中的粒子种群规模为15，最大迭代次数30，控制周期为3 min。风电机组和无功补偿装置采用功率控制模式。

图5为风电场的风速变化曲线，图6为风电场中2号馈线上风电机组的条馈线上的风速波动曲线。

图5 风电场风速变化曲线

图6 2号馈线上的风速曲线

图7为采用本文控制策略前后风电场并网点电压(设取UPCC-ref=1.0(p.u.))随风速变化的变化曲线，从图7可以看出控制后并网电压基本稳定，不再随风速波动而变化。图8为某70 min内一条馈线上机组首末端电压的电压变化，从图中可以看出控制后机组首末端电压电压差为0.005 (p.u.)，相差很小。

图7 并网点电压日变化曲线

图8 一条馈线上首、末机组机端电压变化曲线

为验证本文所提的控制策略在提高风电并网电压的稳定性，均衡机端电压的优势，本文采用3种方式进行仿真验证：SVC和DFIG均参与风电场无功补偿，优先使用DFIG平均分配提供所需的无功，不足部分再有SVG进行补偿；仅用SVC进行风电场无功补偿； SVC和DFIG均参与风电场无功补偿，无功补偿量按本文所提策略分配。

图9、10表明在本文的控制策略下，风电机组的机端电压偏差较小，在方式1的控制下机端电压波动有所改善，但机组的机端电压还有明显波动；方式2控制下机端电压明显扩大，对机组运行的安全性造成了威胁。可见在减小机端电压的差异上，采用本文控制策略与其他控制方式相比具有明显的优势。

图9 50%风电出力工况时机端电压控制效果

图10 满发工况时机端电压的控制效果

6 结 论

针对风电并网电压控制的问题，提出了一种通过控制风电机组无功输出减小机端电压偏差，降低机组因机端电压越限而发生脱网风险的风电场无功电压控制策略，根据风电场的拓扑结构通过潮流计算推导机组间的相互影响及机组的无功调节范围，最后采用智能粒子群算法合理分配机组和补偿装置之间所发的无功量达到无功控制的要求。