模糊情形下的疫情决策与风险管理

潘文全

(岭南师范学院 马克思主义学院，广东 湛江 524048)

一、引言

2018年国务院政府工作报告提出“抓好决胜全面建成小康社会三大攻坚战”,其中包括防范化解重大风险,不幸的是,在2019年年末,武汉发生了一起黑天鹅事件——新型冠状病毒肺炎。这起事件给全国人们带来了很大的影响。反思它的发生发展过程,总结其中的经验教训,优化对重大风险的科学管控,对于建设小康社会具有重要的意义。

总结这起事件的起因,主观方面的原因主要有两个:第一个是认识的模糊性,在武汉市卫健委的前几次通报中,对“是否人传人”的认识不够准确;第二个是在模糊信息下进行了错误的决策,管理者在不清楚新冠病毒是否人传人的情况下,没有制止聚集性活动,也没有有效制止500万人离开武汉回家过年,进而造成了这起全国性的公共卫生事件。事实上,武汉市市长在采访中也表示“各方面对我们信息的披露是不满意的,我们既有披露不及时的一面,也有利用很多有效信息来完善我们的工作不到位的一面,我感觉我们应对危机的能力,公共卫生事件的应对办法还需要很好地完善。”

如何优化对此类黑天鹅事件的应对能力呢?这里面需要解决的核心问题是如何在模糊的情形下进行正确决策。对于任何决策主体而言,只要它遇到这类事件,必然存在认识的模糊性,因为这是一种从未遇到过的事物,没有准确知识积累可以依靠,只能参考一些过去类似的模糊经验,这是客观条件带来的模糊。相对的,任何决策主体本身也具有模糊性,因为它是一个有限的主体,有限的认知能力,不能对所有信息进行合理的处理,很多时候依赖于直觉、经验的指导,很难做出准确的判断,所以在模糊的情形下进行模糊的决策是不可避免的。

对于任何一个决策而言,决策者总是希望它采取的措施能起到积极的作用,要么带来正面的效果,要么消除不好的东西,特别的,在公共卫生事件中,决策者主要考虑的是消除那些不好的影响,即最大程度地降低风险,而不是考虑能获得多少福利,所以应对黑天鹅事件的核心问题就变成了如何在模糊情形下降低公共卫生事件的风险。所幸的是,非精确概率归纳逻辑可以提供帮助,因为非精确概率的研究对象是模糊性,归纳逻辑的一个研究领域是决策,非精确概率归纳逻辑可以优化对公共卫生事件的应对决策。

二、非精确概率归纳逻辑中的决策

非精确概率归纳逻辑是新培根主义概率归纳逻辑的一支,它具有悠久的历史,但直到最近三十年才发展成熟。最早可以追溯到19世纪中期的乔治(B.George)[1]3-64,进一步的发展包括凯恩斯对不完全概率序列的研究[2]78-89;史密斯(C.Smith)对下界和上界下注赔率的讨论[3];威廉(P.Williams)对融贯性的推广[4];厄尔斯伯格(D.Ellsberg)用实验证明了理性决策中不确定性的作用[5-6];邓普斯特(A.Dempster)的多值映射的概念[7],以及谢弗(G.Shafer)对它的解释使得它在人工智能中广受欢迎[8]84-242;但是直到20世纪九十年代,沃利(P.Walley)才促使这个领域发展成熟,他创造了术语非精确概率(imprecise probability简写为IP),给出了下界和上界预期理论的基础,产生了广泛的影响[9]52-109。

非精确概率归纳逻辑理论众多,其中最具一般性的是非精确预期(impreciseprevision)理论,它包括下界预期和上界预期,基石是“赌局”(gamble)概念。假设存在一个可能事件集合,在其上定义一个到实数的映射a,这就是赌局,它表达的是一个不确定的奖励,用一个数值来定量地表达奖励的大小,数值为正表示赌局有正的收益;为负表示带来了一定的损失;为0即保持现状。很明显措施、行动(action)(1)在后文中行动、措施将在同一意义上使用。、决策等都是赌局,它们的结果是不确定的奖励,当然在公共事件决策中主要聚焦于“行动、措施”这类特殊的赌局,注意这里需要在一种宽泛的意义上来理解“行动”,它不仅包括“有为而治”意义上的行动,也包括“无为而治”意义上的行动——保持现状。

假设可能事件集合上的所有措施构成集合L,对于主体而言,某些措施总是可以接受的,比如奖励恒为正的措施;同时接受某些措施意味着接受其它措施,比如主体接受措施a,那么它也就接受了奖励大于等于a的任意措施,但是在很多情况下,措施的奖励可能是正的也可能是负的,主体很难决定是否应该采纳,这时需要对措施的效果做出一个预期,而且这个预期一定是模糊的,前面已经分析了,那么如何来表达这种模糊的预期呢?

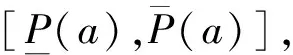
通常决策主体为了实现自己的目标,都有多种行动方案,每种方案又是由多个行动、措施组成的,所以主体选择的是一个最优行动方案,而不是单个的行动。上面已经用预期区间表达出了决策时的模糊性,如何使用它来选择合理的行动方案呢?合理的第一层含义是不选择有害的方案,其次才是选择最优的方案。

(一)不选择有害的措施

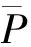
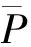
如何直观地理解它呢?假设存在三个措施a1,a2,a3,在a1和a2之间决策主体认为a1更好;在a2和a3之间认为a2更好;在a3和a1之间认为a3更好,这就意味着决策主体为了得到a1,就必须放弃a2外加一些其它损失;为了得到a2必须放弃a3外加一些其它损失;为了得到a3必须放弃a1外加一些其它损失。现在主体手头有措施a1,它用a1外加一些损失换来了a3,再用a3外加一些损失换来了a2,再用a2外加一些损失换来了a1,最终的结果是主体手头还是a1,但是在这个过程中他蒙受了很多的损失,处境比开始的时候更糟,所以选择这三个措施就是不理性的,它们招致了确定的损失,相反的就是避免确定损失。简单地说,主体不能接受下述行动方案:方案中的每个措施都是可接受的,但是这些措施组合起来却会带来损失。

在这次新冠肺炎的爆发初期,管理者无意中就采取了招致确定损失的行动方案,以致于疫情愈加严重。在这个方案中共有三个主要措施,它们分别是2020年1月1日宣布停业华南海鲜市场(简写为措施a1);在1月20日之前没有对聚集性活动进行任何管制(措施a2);没有有效控制500万人离开武汉回家过年(措施a3),后两个措施是保持现状。每个措施在当时的决策情境中都是可接受的,不然也不会被主体采纳,但是这三个措施组合起来,却构成了一个会造成极大损失的行动方案。注意当某个方案招致确定损失时,并不意味着一定会遭受损失,只是意味着主体倾向于采取带来确定损失的措施,所以很多决策者出于侥幸的心理无视这一原则,这也是新冠肺炎爆发的一个决策方面的原因。

所以在进行决策时,首先要做的是使用避免确定损失来判定行动方案,虽然满足此标准的行动方案不一定是最优的,但至少是无害的,这也体现了在公共事件决策中“防范化解重大危机”的思想。如果决策主体已经选择了避免确定损失的某个行动方案,这又意味着什么呢?事实上,避免确定损失原则在非精确概率归纳逻辑中的作用类似于一致性在经典逻辑中的作用[11],在经典逻辑推理中,从一个一致的前提总能推出一些结论,在这里也是同样的,从一个避免确定损失的行动方案出发,能够推出它对其它措施的影响,即推出主体对其它措施的预期范围。

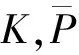
在经典逻辑推理中,当前提不具有一致性时,可以推出任何结论,致使推理丧失价值。在这里,当前提不满足避免确定损失时,自然扩张推出其它措施的上界预期值为负无穷,也使得决策毫无价值。因为不管措施结果如何,如果主体的行动方案总是带来损失,那么在某些条件下此行动方案有可能使得主体的损失变得无穷大,所以决策的第一步总是判定前提是否避免确定损失,其次才推导它在其它措施上的结果。

(二)选择最优的措施

虽然有时候决策主体选择了一个不那么差——避免确定损失——的行动方案,但是在构成这个方案的所有措施中,并不是所有的措施都是最优的,然而决策者总是想挑选出最好的措施。这时需要一对重要的过渡概念——非严格优于(almost-preferred)与严格优于(strict preference),它们被用于描述和比较不同措施之间的优劣。

这对概念是什么意思?假设存在一个措施集K+,任何时候决策者都愿意接受里面的措施,那么它就是(严格)可取措施集。相对的,假设K是另一个可取措施集,对于其中的任意措施a和奖励δ,决策者倾向于接受措施a+δ,但不一定倾向于接受措施a本身,那么K就是非严格可取措施集。沃利发现下界预期和非严格可取措施集可以相互转化;下界预期与严格可取措施集也能相互转化[9]52-160。比较下界预期和措施集,可以看出措施集提供了更多对决策有用的信息,因为可以区分严格措施集与包含它的非严格措施集,但是由它们转化出的下界预期却相等,所以在决策中它们是一对更加基础的概念。

有了可取措施集和非严格可取措施集就能得出优于的概念。措施ai非严格优于aj当且仅当ai-aj属于非严格可取措施集K,它的直观含义是决策者不反对用aj交换ai,ai-aj优于或者等同于现状,采取里面的措施所导致的结果不会比现状更差。但是在选择时,决策者需要知道严格优于而不是非严格优于,因为在措施ai和措施aj之间,ai严格优于aj,决策者一定会选择ai,但是措施ai非严格优于措施aj,它可能会选择aj,导致决策失误。ai严格优于aj当且仅当ai-aj属于集合K+,它表示决策者渴望用aj交换ai,采取里面的措施所导致的结果只会比现状更好。

用这对概念来分析促使新冠肺炎全国爆发的那几个措施,可以清晰地看出它们的优劣。在万家宴举行前,举办方曾向决策者反映,鉴于疫情是否取消活动,当时决策者就面临两个行动——ai取消与aj照旧——的抉择,在决策者看来,“取消”非严格优于“照旧”,所以选择了照旧举行,导致决策失误。在1月23日,武汉下令封城,但是前后还是有500万人离开武汉,令行动ai=500万人离开武汉;aj=500万人留在武汉。在这500万人看来,它们认为措施ai非严格优于aj,即离不离开武汉和现状差不多,但是在政府管理者看来,措施ai严格优于aj,它们渴望用aj交换ai,如果这500万人没有离开武汉,肺炎至少不会波及全国,不会造成其它省市几周的停工,经济损失将减少几万亿人民币,这也是措施ai的上界预期值。

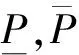
(三)一个决策的例子

下面给出一个决策的实例。假设可能空间集由任意多个城市构成,现在为了达成某个目标,决策主体考虑在这些城市中采取措施a1,它的效果如下:

表1 奖励表

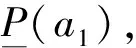
现在考虑另外一个行动a2,它的奖励如下:

表2 奖励表

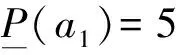
现在专家向决策者提供了另一个措施a3,并且给出了它在各个城市的预期效果:

表3 奖励表

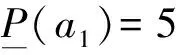
在这个例子中,三个措施是在一般意义上而言的,为了计算的简便,对它们的收益也进行了简化。在本次肺炎的防治中,这三个措施可以被明确为:a1代表管理传染源;a2代表切断传播途径;a3代表保护易感人群,当然他们的收益值也会大不一样,但是决策方法是一致的。

三、风险的评估

对于任意决策主体而言,关心措施、行动的收益是决策时考虑的首要因素,只有收益足够吸引人,行动才会被落实。相对的,任何行动都有失败的可能,一旦失败不仅实现不了预定的目标,还会造成恐慌、带来损失,这就是行动的风险,很明显任何主体都会选择风险低的行动。特别的,在处理黑天鹅事件的决策中,主体主要关心风险,毕竟这类公共安全事件一旦发生,只会带来损失,毫无收益可言;另一方面,面对威胁反应过度、矫枉过正,还会加大损害,所以准确地评估各种措施、行动的风险就显得尤为重要。

(一)评估措施的风险

风险评估的核心问题是衡量措施的危险程度,目前存在多种衡量方法,最常用的是风险评估ρ。对于任意措施a,ρ(a)是一个实数,它用具体数值总结了措施的风险,当它取值为正时,表示决策者为了应付措施可能带来的损失,需要预备的最少风险资金;当它为负,表示在保持措施可接受的条件下,可以从中减去的最大金额;当它为0表示措施的风险刚好位于临界点。在公共事件的应对中,风险评估值一般为正数,因为这类事件一旦处理不当,就需要花费很大的代价才能弥补损失,通常为经济损失。更进一步的,假设K为任意措施集,可以考虑以它为定义域的风险评估ρ。

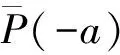
为了使用非精确概率归纳逻辑的推理方法,首先需要寻找一个避免确定损失的前提,然后使用自然扩张推出结论。这个前提通常表现为专家提出的某个行动方案,它由一系列的原子行动、措施构成,比如在新冠肺炎的防治中,专家就提出了控制传染病的行动方案,包括管理传染源、切断传播途径、保护易感人群,进一步的,这个方案又可以细分为很多具体的原子行动、措施,比如管理传染源就包括隔离治疗患者、医学观察接触者等;切断传播途径包括封城、禁止聚会等;保护易感人群包括研发药物、疫苗等,当然还可以细化为更加具体的行动。

通常专家给出了方案,也会对方案中的行动给出一个风险判断,这就是定义在方案上风险评估,在这里就是防疫失败将会造成的损失。比如依据新冠肺炎防治方案的结果,专家对风险给出了一个模糊的估计,他们认为有三种可能结果:一、最好的结果是2～4周内所有病人治疗结束,2～3个月内全国疫情得到控制;二、最差的结果是控制失败,病毒席卷全球;三、胶着的结果是病例数在可控范围内增长,抗疫过程会十分长,可能长达半年至一年之久。那么为了弥补这些潜在的损失,需要多少代价呢?依据疫情对GDP的影响可以给出大致的估计:最好的结果损失了一个月的GDP;胶着的结果损失了一年的GDP;最差的结果当然损失更大。由于风险值等于主体为了承担行动的风险所准备的最低资金,所以肺炎防治方案的风险值就是一个月的GDP,大约是8万亿人民币。

当然这个数据是建立在把方案看成只包含一个行动而得出的,很明显它满足避免确定损失,采用它不会带来荷兰赌——一定会失败的赌局。通常方案中包含多个行动,每个行动由不同的主体实施,比如封城就是由不同的城市管理者实行的,这就可以看成是不同的行动,不同的城市管理者依据对本城的影响来评估行动的风险,这就可能有成千上万个行动,这时必须使用大数据依据避免确定损失的公式进行判定。

即使方案中的行动个数足够多,它也不能包含所有的行动,因为决策主体当前可调动的行动资源是有限的,那么就存在一些潜在的行动没有被囊括在方案中,但是它们有可能需要落实,特别的,当已经确定了某个方案时,它会对后续的行动产生限制：限制后续行动的选择;限制后续行动的效果;影响后续行动的风险,比如“500万人离开武汉回家过年”就造成了其他城市要承受感染的风险。为了评估这些潜在行动的风险,就需要自然扩张。假设存在一个行动方案,已经得出了其中行动的风险值,且它避免确定损失,如何推出其它行动的风险值?这是风险推导要处理的核心问题。由非精确概率归纳推理可知这一步是由自然扩张完成的,它可以得出其它任意行动的风险值。

(二)一个风险评估的例子

在前面例子的基础之上,继续讨论风险评估。假设可能空间集由任意多个城市构成,现在为了达成某个目标,决策者考虑分别在这些城市中采取三种行动a1、a2、a3,在本次肺炎的防治中,a1代表管理传染源;a2代表切断传播途径;a3代表保护易感人群,它们的预期收益如下:

表4 收益表

四、结语

非精确概率归纳逻辑在公共危机决策上的运用具有多种优缺点,首先关注优点,然后过渡到缺点。

优点主要是针对传统决策理论——贝叶斯决策理论——而言的。相比贝叶斯理论,它不以概率分布为起点,而是以预期为基础概念,适用于不可积或者难以计算积分的地方,在理论形态上体现为非精确性,能够处理模糊认知的情况,比贝叶斯决策适用面更广[5]。其次,非精确概率归纳逻辑属于统计推理中的非严格贝叶斯推理,它具有其它统计推理不具有的优势,不以概率的频率解释为基础,又能够充分利用样本之外的其它信息,使得结论更加充分,决策更加合理。最后,它用一种理论统一地给出了模糊决策和风险评估的方法,即非精确概率归纳逻辑中的避免确定损失和自然扩张,这既丰富了理论的内涵,又便于决策者的使用。总之这些优点是对比精确概率而言的,在决策中就是针对基于精确概率的贝叶斯决策理论而体现出来的[13]。

缺点主要体现在两个方面的:一、决策复杂;二、自然扩张的问题,其中每个缺点又都包含两个层次。首先关注第一个缺点——决策的复杂。复杂的第一个层次体现在行动方案是否避免确定损失的判定上,从它的判定公式可以看出,当方案中的行动个数为n时,至少要判断2n-1次公式是否成立,计算量相当大。复杂的第二个层次体现在自然扩张上,很明显它的计算量也是人力难以胜任的,特别是当行动的个数增多时,不等式右边部分的组合数呈现指数式的增长,即使行动的个数很少,人力也是不堪重负,这可以从上述决策实例中清楚地看到。因此庞大的决策计算负荷是运用的一个缺点,在使用过程中非常繁琐,至少人类大脑难以驾驭,只能求助于大数据,当发展出了对应的决策软件之后,人类在科学决策的能力上将得到极大的提升。

综上所述,认识的不充分与决策的紧迫感是公共危机决策中的困难所在,非精确概率归纳逻辑可以解决这个问题,其中的关键方法是避免确定损失和自然扩张,避免确定损失能够挑选出无害的措施;自然扩张能挑选出最优的措施,同时这一方法还能评估行动方案的风险,因为风险评估可以还原为预期区间。相对于一般的决策方法,本方法最大的优点是能够用于黑天鹅事件等模糊情形,美中不足的是决策计算量偏大,需要大数据的支持。