基于凸优化理论的和、差波束方向图合成新方法

祁峥东, 邱明华, 蒋莹莹, 孔 玥, 黄 晟

(1. 中国船舶集团有限公司第八研究院，南京 211153 ；2. 南京大学 电子科学与工程学院，南京 210046 )

0 引 言

波束合成技术是阵列信号处理研究领域中的关键研究方向，其内容包括对接收阵列信号的加权处理，以使方向图主瓣对准期望角，零陷位置对准干扰角，从而提高系统的性能。该技术在声声呐、雷达、通信等领域中得到了广泛的应用，在方向图综合问题中通常要求具有低副瓣特性。通过各类算法，理论上[1-6]可以设计出具有超低副瓣电平的远场方向图。但是，由于仿真和实际加工存在各种误差，如单元之间的互耦效应、单元位置加工误差、通道响应失配，以及单元的幅相误差等因素，提高了最大副瓣电平。此外，所设计的远场方向图应具有较好的方向性(如对应较窄的主瓣波束)。因此，综合过程应在最大副瓣电平和主波束宽度之间进行平衡。和、差波束方向图因在实现角度估计和目标跟踪方面发挥着特殊的作用，使得这一研究方向一直以来受到很多学者的重视，目前已有很多技术成果问世。[7-11]

随着军民两个领域对雷达分辨率、灵敏度等性能指标的要求不断提高，使得雷达阵列朝着超大型规模发展。这一实际要求使雷达成本大幅提高，促使稀疏阵相关的研究得到越来越多的关注。稀疏阵的阵元合理的布置可以在不影响一些技术指标的前提下有效降低天线单元和通道总数,从而降低系统的造价和馈电网络的复杂度。稀疏阵的单元位置优化和单元数量最少化问题实际属于非线性优化范畴，以往经典解决方案包括采用智能优化算法、模拟退火法、遗传算法、蚁群优化算法和粒子群算法等。作为高效的全局优化算法，智能优化算法已在阵列方向图综合领域得到大量应用，并取得了良好的应用成果[12-15]。但是，此类算法存在运算量大、易陷入局部最优、对初值敏感、收敛速度慢的缺点，尤其对大型天线阵列进行综合优化时阵元单元数量的激增会导致算法的计算负担增大。

稀疏阵综合的目的为使得阵列中单元数量最少化，即完成方向图性能指标的同时从等间距栅格的满阵中选择数量最少的单元。此问题为L0范数最小化综合问题，为NP-Hard困难问题。本文结合压缩理论用重加权L1范数优化算法替代原先L0范数算法以完成阵元数量最小化的设计目标。这一过程将非凸优化模型转换成凸优化(Convex programming)模型求解。

本文提出的以降低馈电系统复杂度为目的设计可分为两类，第1类是通过优化使得和、差波束模式下在部分单元上共用激励，第2类降低系统复杂度的方法是通过减少天线阵列中单元总数。本文算法将共用单元部分加权和单元级加权作为统一优化目标，以减少阵列中单元总数，而将涉及的辐射性能指标(如差方向图斜率，以及和、差波束的主瓣宽度、最大副瓣电平等)利用凸优化算法转化为凸问题进行求解。

与经典算法结果相比，本文基于L1范数最小化的稀疏阵综合方法与凸优化方法相结合的算法在提高某些方向图辐射性能的同时可以有效减少阵列中单元的个数，从而有效简化馈电网络。

1 算法应用模型

1.1 远场方向图模型

这里以平面阵列模型为例介绍本文算法，考虑2M×2N元的矩形阵列，其中沿x轴布置2M行单元，沿y轴布置2N行单元。各阵元等间距排布，dx和dy分别表示沿x轴和y轴阵元间距，远场方向图这里表示为

(1)

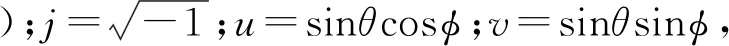
a=[a1，1,a1，2,…,a2M，2N-1,a2M，2N],

w(u,v)=ejβ[(-M+1/2)du+(-N+1/2)du]

=ejβ[(-M+1/2)du+(-N+3/2)du],…,

=ejβ[(M-1/2)du+(N-3/2)du]

=ejβ[(M-1/2)du+(N-1/2)du]

远场仰、方位差波束输出分别为

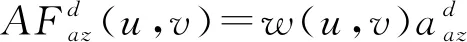
1.2 凸优化方法

本文将凸优化算法应用于和、差波束方向图综合问题，以期减少阵列中可变增益放大器和单元总数的同时提高方向图性能，优化问题表述为

|w(u,v)as|≤ρs(u,v)(u,v)∈SLs,

|w(u,v)ad|≤ρd(u,v)(u,v)∈SLd,

(2)

这里，远场和、差波束方向图|AFs/d(u,v)|2的主瓣SBs/d以逼近期望和、差波形ds/d(u,v)为目的，这里有d(u,v)∈R+，其中，s、d分别表示和、差波数。|AFs/d(u,v)|2与ds/d(u,v)之间的距离εs/d尽可能地缩小。副瓣部分(SB)的峰值电平应该小于ρs(u,v)。式(2)中，控制和、差波束主瓣宽度的约束问题为非凸函数。本节对以往凸优化算法进行改进，引入双变量的多凸优化算法，通过循环逼近的多凸模型来求解控制主瓣宽度的非凸问题，式(2)内容转化如下：

(3)

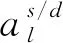
(4)

本节选择文献[16-19]中的基于迭代傅里叶技术获得的满足式(4)的阵元激励权值作为迭代过程的初值。

1.3 迭代加权L1范数理论

本节将压缩感知理论应用于单脉冲天线和、差波束合成技术中。为使阵列中单元总数尽可能少，稀疏阵列的综合问题可表述为

(5)

式(5)为阵列中激励值为0的单元数量。稀疏阵综合的目的为使得阵列中单元数量最少化，即完成方向图性能指标的同时从等间距栅格的满阵中选择数量最少的单元。此问题为L0范数最小化综合问题，为NP-Hard困难问题。为解决此问题，利用重加权L1范数优化算法完成设计目标，可表述为

(6)

其中

和、差波束形成中共用阵元激励的约束可表示为

(7)

式(7)是线性规划问题。在迭代过程中，未知变量减少数量为Ψ个。 在迭代过程中，上一步的封闭解将作为下一步迭代的初值。阵列天线和、差波束的综合问题在第n+1次迭代过程中激励约束表述为

(8)

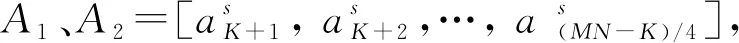
(9)

2 计算实例

为了验证本文提出的算法，本节选择文献[10]中凸优化算法综合得出的例1作为参考对比算例。

本节所有仿真验证均采用台式计算机，硬件参数如下：处理器：Intel® CoreTMi5-6500T，RAM为12 GB；仿真软件为MATLAB，版本为R2018a。式(8)中μ值选择固定值0.001。

例1中，初始阵列选择口径为5λ×5λ的正方形平面阵，且各阵元等间距排布，沿x轴和y轴阵元间距均为0.5556λ。设两列共用单元，位置分布在{m=1,…,10,n=1,10}，即这两列单元在和、差波束形成过程中共用激励。图1和图2给出了本文提出算法得出的三维远场方向图，相应的阵元激励与位置分布如图3和图4所示，仅画出稀疏阵第三象限内的阵元分布和激励值。综合得出和波束的方向性系数值为19.03 dB，方位差波束斜率值为[∂AFdaz(u0,v0)/∂u]|u=u0,v=v0= 22.14 dB。

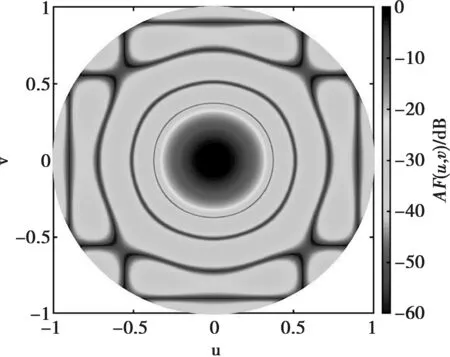
图1 和波束三维方向图的二维投影

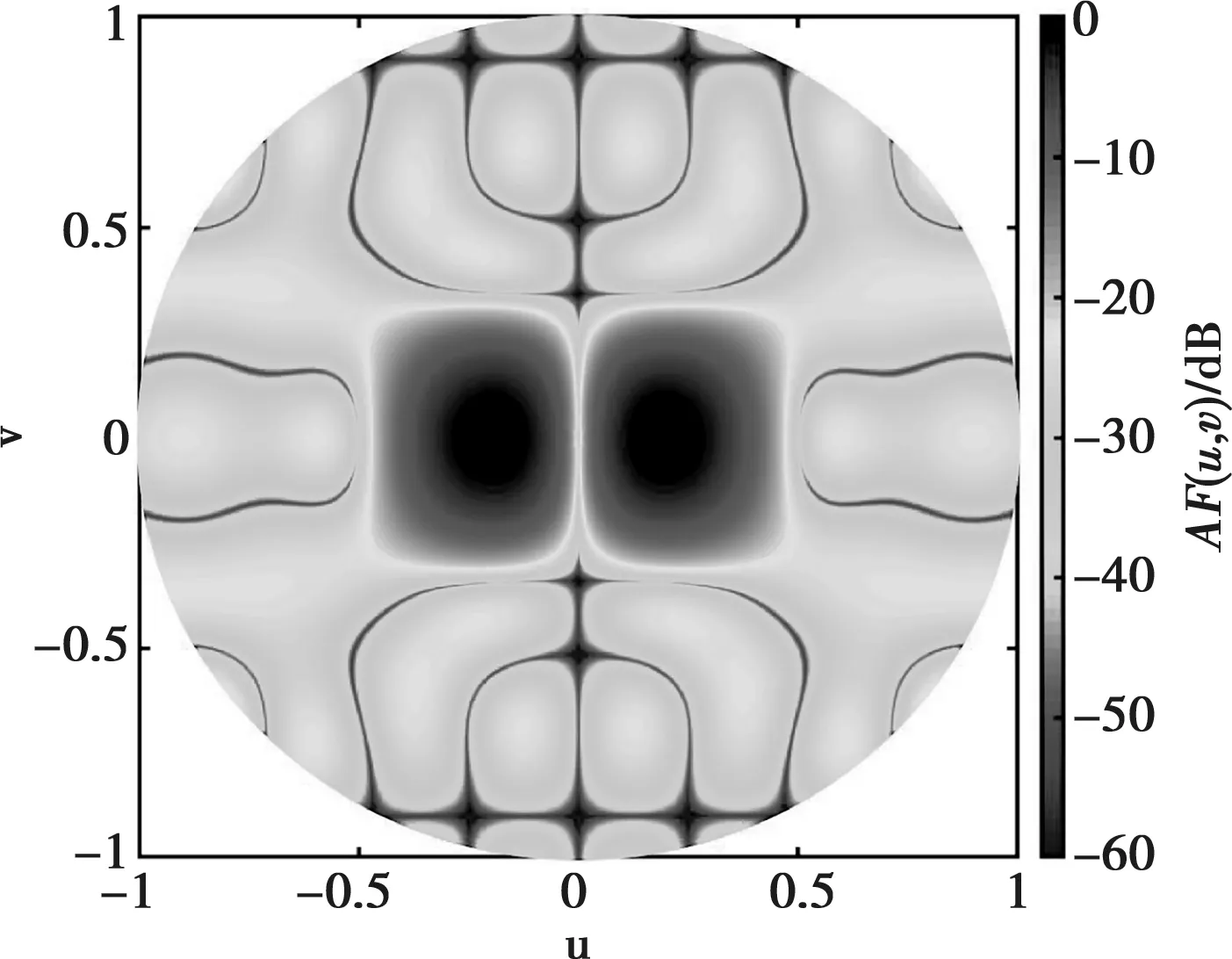
图2 方位差波束三维方向图的二维投影

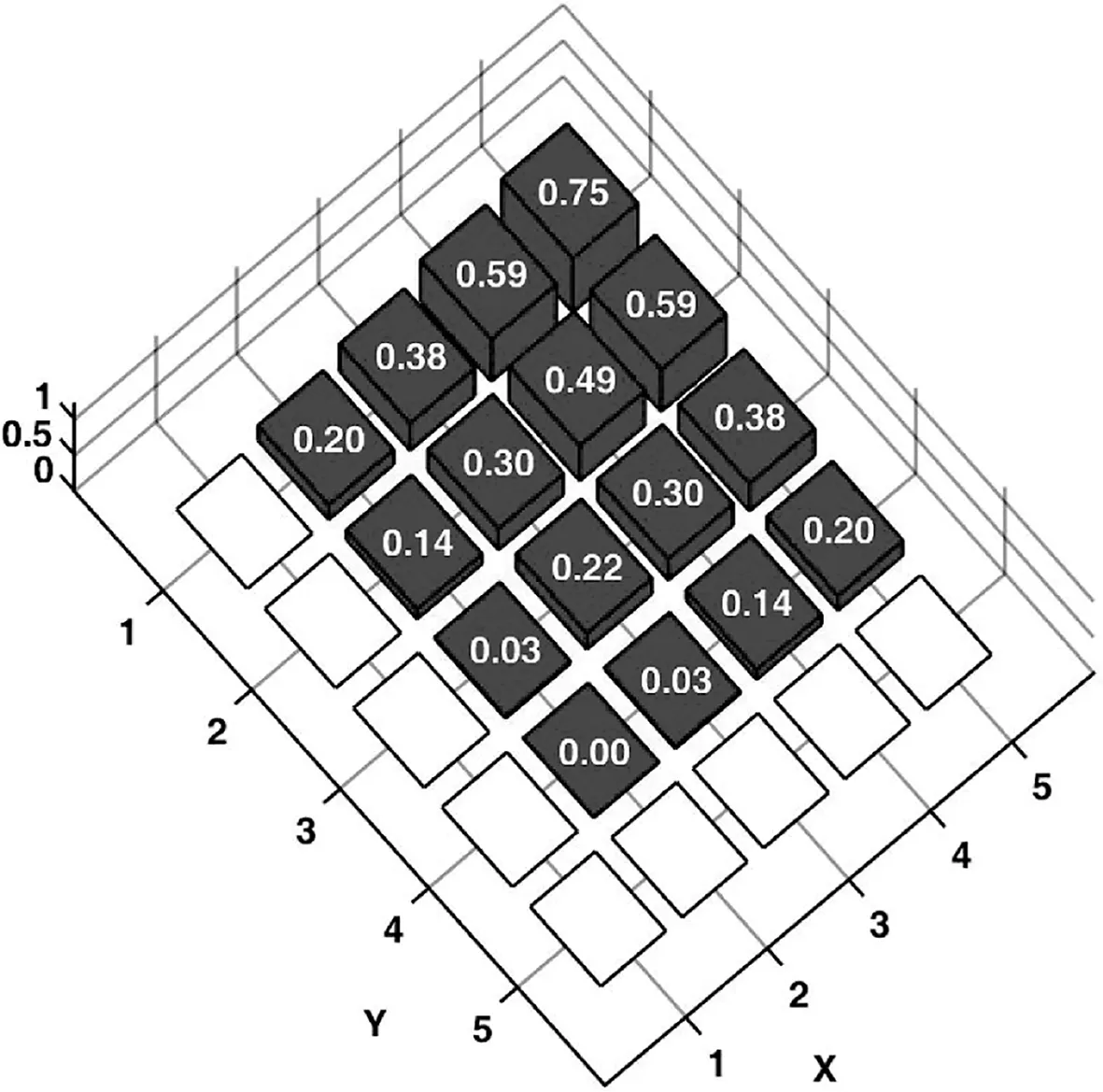
图3 和波束对应激励幅度

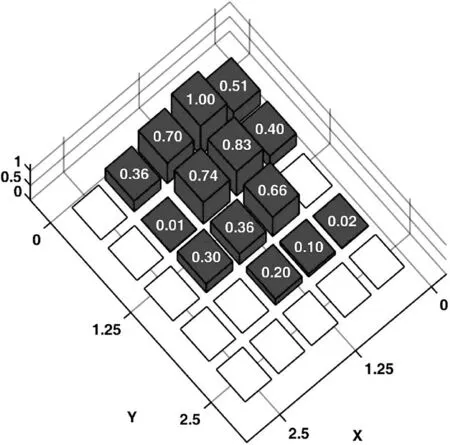
图4 差波束对应激励幅度

由表1中可以看出，和波束副瓣区域最高电平为PSLs=-32.8 dB，方位差波束副瓣区域最高电平为PSLdaz=-22.9 dB。综合后的和、差波束在u=0、v=0方向上的半功率波瓣宽度(Half-Power Beamwidth，简称HPBW) 分别为HPBWPsu=0.27和HPBWsv=0.27，HPBWPdu=0.21和HPBWdv=0.27。与文献[10]中LP算法综合出的结果相比(如表1所示)，本文方法不仅实现了更低的最大副瓣电平(Peak Sidelobe,简称PSL)，并且获得了更窄的波束宽度。与文献[10]中的设计相比，本设计中“开”状态的阵元数量在和、差波束两种模式下分别减少了36% 和44%。此外，本设计中可变增益放大器(Variable Gain Amplifier，简称VGA)数量节省了30%，同时阵列孔径减少了23.5%。

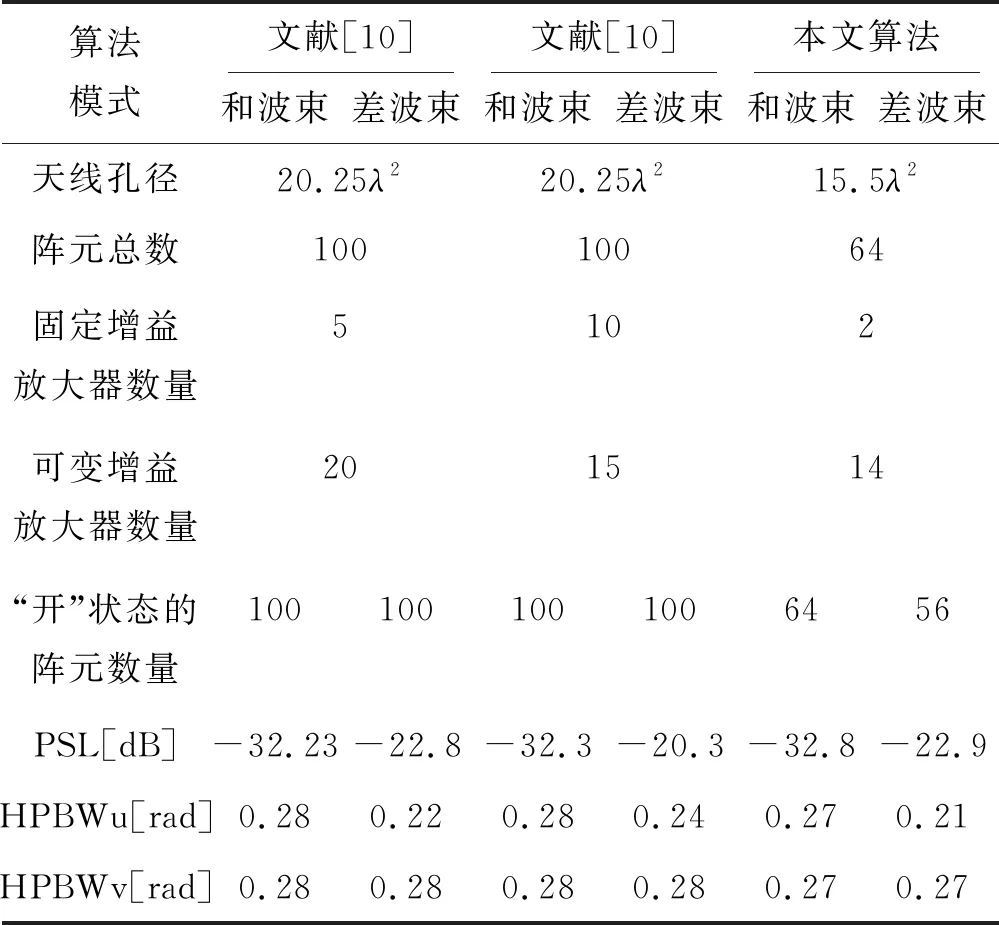
表1 本文算法与文献[10]中LP算法的性能对比

例2中，初始阵列选择口径为5λ×5λ的正方形平面阵，且各阵元等间距排布，沿x轴和y轴阵元间距均为0.5556λ。设两列共用单元，位置分布在{m=1,…, 10,n=1, 10}，即这两列单元在和、差波束形成过程中共用激励。 图5和图6给出了本文提出算法得出的三维远场方向图，相应的阵元激励与位置分布如图7和图8所示，共用激励用深黑色标记。综合得出和波束的方向性系数值为19.23 dB，方位差波束斜率值为[∂AFdaz(u0,v0)/∂u]|u=u0,v=v0= 23.05 dB。由表2中可以看出，和波束副瓣区域最高电平为PSLs=-21.5 dB，方位差波束副瓣区域最高电平为PSLdaz=-16.5 dB。综合后的和、差波束在u=0、v=0方向上的HPBW分别为HPBWPsu=0.27、HPBWsv=0.21、HPBWPdu=0.18和HPBWdv=0.23。与文献[10]中LP算法综合出的结果相比(如表2所示)，本文方法在实现了相同的最大副瓣电平值的同时获得了更窄的波束宽度。与文献[10]中的设计相比，本设计中“开”状态的阵元数量在和、差波束两种模式下分别减少了40%和44%。此外，本设计中VGA数量节省了45%。

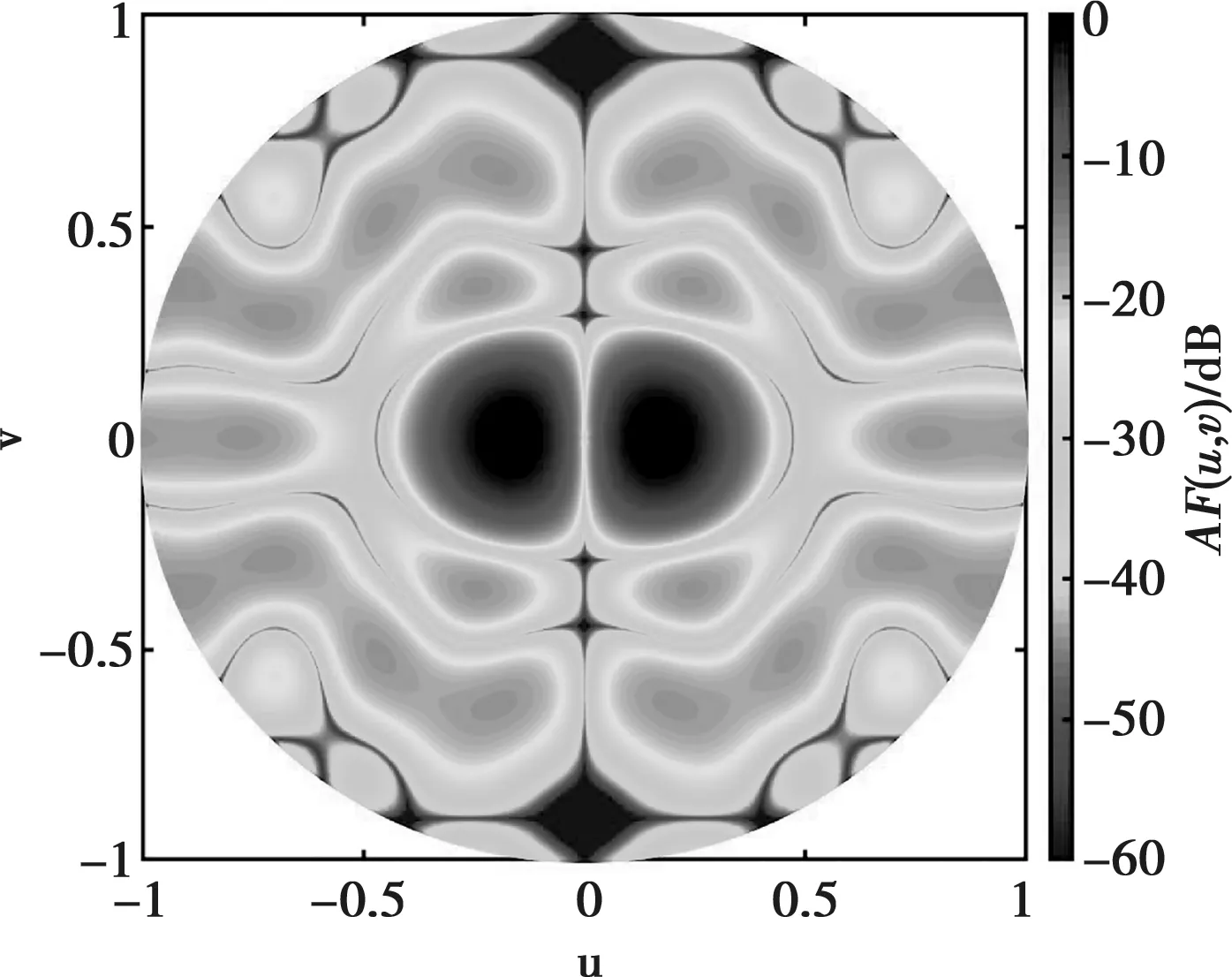
图6 方位差波束三维方向图的二维投影

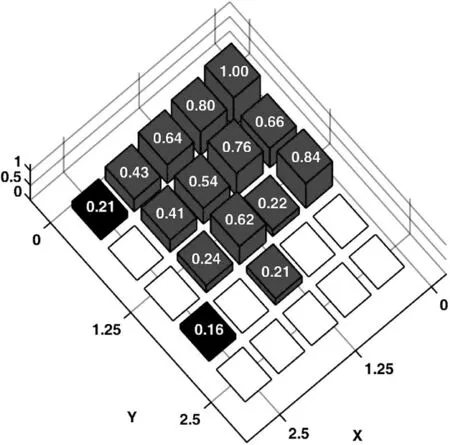
图7 和波束对应激励幅度

3 结束语

本文提出了一种采用凸优化算法与压缩感知理论相结合的和、差波束方向图合成新方法，将控制和、差波束的主瓣宽度的非凸约束问题转化成凸约束问题进

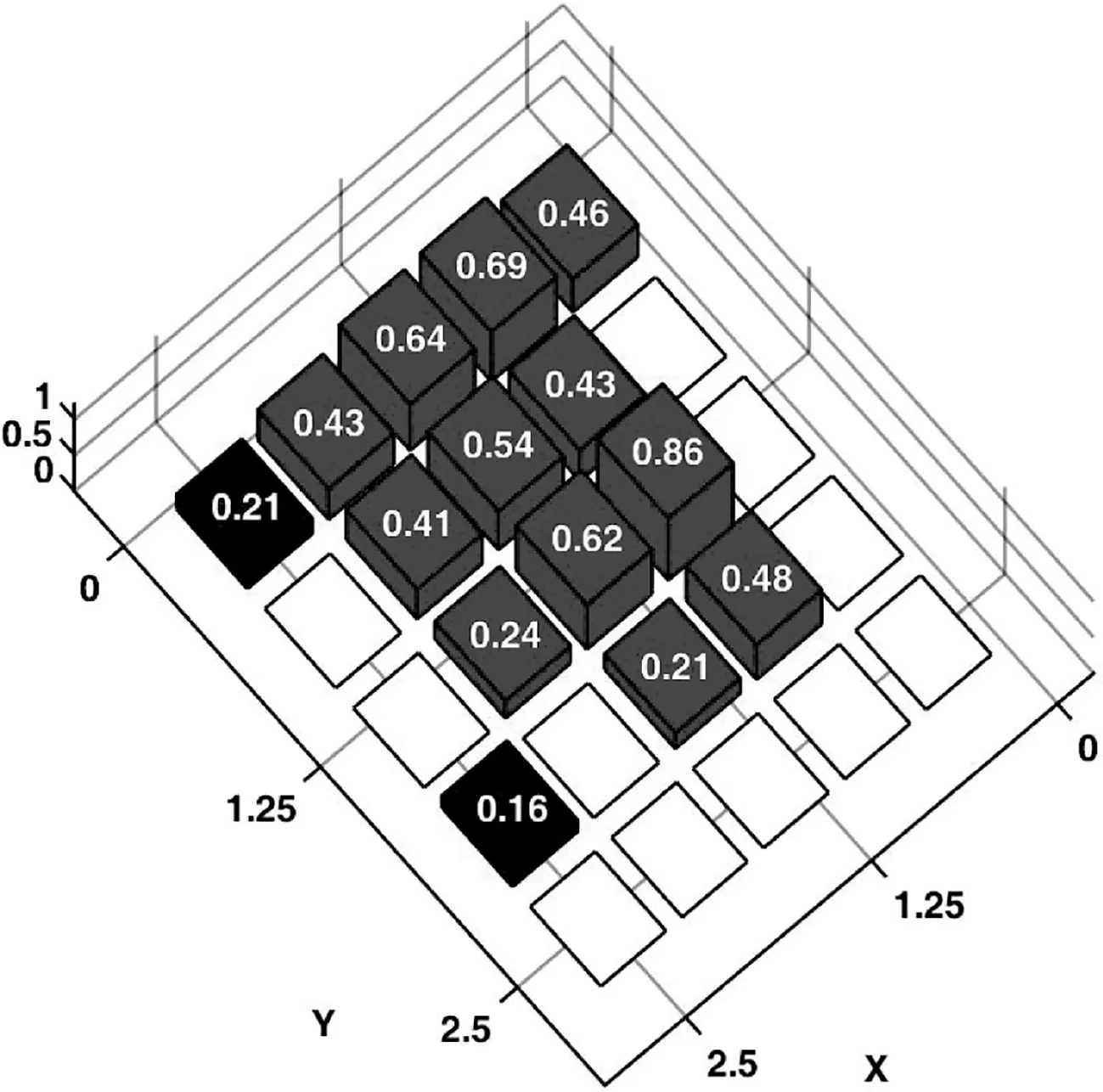
图8 差波束对应激励幅度

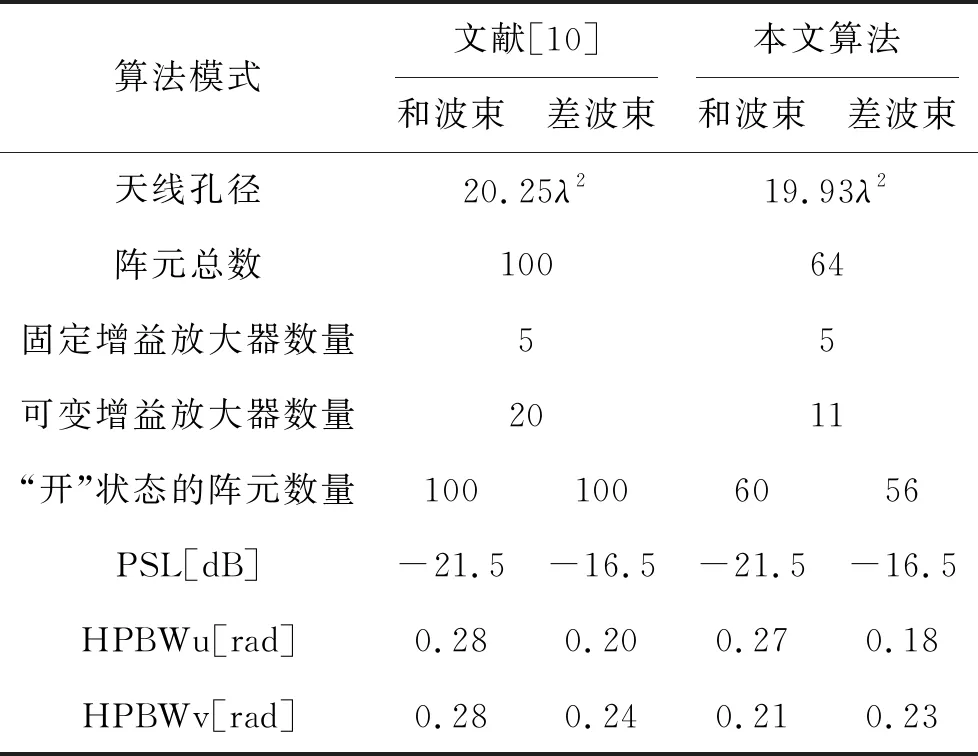
表2 本文算法与文献[10]中LP算法的性能对比

行求解, 并结合压缩理论用重加权L1范数优化算法替代原先L0范数算法以完成阵元数量最小化的设计目标。这一过程将非凸优化模型转换成凸优化模型求解。本文提出的以降低馈电系统复杂度为目的设计可分为两类，第1类是通过优化使得和、差波束模式下的部分单元共用激励，而第2类降低系统复杂度的方法是通过减少天线阵列中单元总数。本文算法将共用单元部分加权和单元级加权作为统一优化目标，以减少阵列中单元总数。不同方向图要求的稀疏平面阵综合结果表明，与现有的和、差波束优化算法相比，本文算法具有很好的普适性，综合得出的和、差方向图性能更优且所需的阵列单元总数、可变增益放大器总数均更少。