中深层套管式埋管换热器逆向传热现象的研究

贾林瑞崔萍方亮方肇洪

(1.山东建筑大学 热能工程学院，山东济南250101；2.济南有方新能源科技有限公司，山东 济南250101；3.山东中瑞新能源科技有限公司，山东 济南250101)

0 引言

地源热泵技术利用了岩土层中的冷热源为建筑提供所需的冷热量，属可再生能源利用技术，与传统空调系统相比，在节能环保等方面有着无可比拟的优势。传统地源热泵的地埋管钻孔深度通常只有100～200 m，可利用的地热资源有限，且对冷热负荷平衡要求较高[1]。同时，地埋管换热器需要一定的地表面积布置钻孔，这也极大地限制了该技术的应用和推广。中深层地埋管换热器的埋管深度可达2 000～3 000 m[2]，因此单位占地面积的中深层地埋管换热器的取热量远大于浅层地埋管的取热量，所需的钻孔面积大大减少。地下深层岩土温度可达70～90℃[3]，较高的岩土温度可以较好保证冬季取热的持续性。中深层地埋管换热器技术的出现，将浅层地热能利用的地源热泵技术拓展至中深层地热能利用范畴。但由于该技术处于发展阶段，技术不完善导致初投资较大。目前，有众多研究将中深层地埋管换热器布置在废弃油井中，从而在一定程度上减少了初投资[4-6]。在中深层地源热泵系统中，地下部分的换热器多采用套管式换热器，而不是U形管换热器。根据已有的研究发现，套管式换热器换热效果更优[7]。

关于浅层地埋管换热器的传热分析已有较为成熟的模型。求解模型通常分为钻孔内、外两部分，钻孔内的模型多采用稳态导热，钻孔外的模型为瞬态导热模型。求解钻孔内流体温度的模型包括一维、二维以及准三维导热模型。其中，可利用一维导热模型计算流体至孔壁的热阻，而利用二维导热模型和准三维模型又可计算单U、双U以及套管式换热器内流体温度在深度方向上的变化。计算钻孔内流体温度的前提是得知钻孔壁温，而其可通过钻孔外的模型计算得到。目前，钻孔外的计算模型主要包括线热源模型、面热源模型等解析解模型和数值传热模型等。这些模型通常假设初始地温均匀，因此只适合在研究浅层地埋管换热器的过程中使用。由于中深层埋管换热器传热区域涉及的地温梯度较大，且大地热流的存在也增加了解析解的求解难度，因此直接将传统的浅层地埋管传热模型应用于中深层换热器传热分析会产生一定的误差[8-10]。

由于中深层地埋管传热问题的复杂性，更多学者采用数值解法分析这些问题。HOLMBERG等[11]运用有限差分法建立了岩土层及循环流体的节点方程组，并通过矩阵分裂的方法，求出了岩土及流体的温度，分析了流体流向对温度分布的影响以及对延米换热量在深度方向变化的影响。在运行过程中通过增加流速从而提高运行效率，地埋管从地下取热时，循环液从外管进入内管流出的模式传热效率高；而在向地下岩土放热时，内进外出模式的传热效果更好[11]。FANG等[3]运用交叉差分的方法建立了岩土内部的节点方程，运用追赶法求解出了岩土温度场，并与解析解模型进行了对比分析，发现了流体在管道内流向对进出口温度并没有直接影响，对于套管式换热器而言，选用低导热系数的内管材料可以显著提高套管式埋管换热器的性能。LIU等[12]提出了一种充分考虑地温梯度和内管热量损失的数值解模型。

除了自行编写数值模型以外，还可以利用现有的商业数值模拟软件，如ANSYS、FEFLOW和COMSOL等，对中深层地埋管换热器进行传热分析。MORGAN等[13]利用FEFLOW建立了深度为5 000 m的地埋管换热器传热模型，分析了分别运行6个月和25年后出口温度、延米取热量、热影响区域的变化情况。搭建实验平台进行实验研究是分析中深层地埋管换热器传热性能最直接的方法，刘俊等[14]通过实验结合数值模拟的方法，分析了中深层地埋管换热器性能和地源热泵系统性能，发现适当增加外管径、减小内管径有利于深层地埋管换热器换热，内管敷设保温层可有效地降低套管换热器的换热损失，但流量较大时，过长的保温层对套管的换热作用并不明显。PAN等[15]和FANG等[16]在套管式准三维解析解模型的基础上，建立了考虑地温梯度在内的钻孔内流体传热过程的解析解模型，与已有的模型进行了对比验证，分析了各运行参数对地埋管换热器运行效率的影响，发现该模型具有较高的计算精度，可在一定程度上提高计算效率。

在某些取热运行工况下，当从深层岩土区返回的循环水温度高于周边岩土温度时，会出现循环水加热岩土而产生的逆向传热现象。逆向传热现象对整个埋管的换热是不利的，应采取一定的措施尽可能减少逆向传热区域，或对逆向传热区埋管进行保温处理。目前，国内外关于浅层埋管区的逆向传热现象的研究并不多。文章将在已有数值模型的基础上，研究中深层换热器的逆向传热现象，模拟温度场的分布，分析主要运行参数和相关物性参数对逆向传热区深度的影响，其结论对提高中深层地埋管地源热泵工程系统能效具有参考价值和指导意义。

1 中深层套管式地埋管换热器传热模型

1.1 套管式地埋管换热器的传热模型

中深层套管式换热器分为外管和内管，内外管在底部连通。套管式换热器中流体流动的方向对换热效果影响较大，经验证取热时采用外进内出的效果较好[11]，因此文章采用外进内出的流动方式。套管式换热器结构图及物理模型如图1所示，外进内出的流动方式如图1(a)所示，流体在循环水泵的驱动下由内外管间的环形通道流入，沿着环形通道下降，在换热器底部进入内管，流体沿着内管上升并在内管顶部流出，进入热泵机组实现供热。

数值传热物理模型如图1(b)所示，其中i、j分别为半径和深度方向节点；Tf1和Tf2分别为进水和出水水温，℃；r为岩土层径向位置，m；z为钻孔深度方向的轴向坐标，m；Ta为地表以上的空气温度，℃；ha为地表表面对流传热系数，W/(m2·K)；Hb为数值计算区域底部边界深度，m；rbnd为数值计算区域径向边界宽度，m。

图1 套管式换热器结构图及数值传热物理模型图

理论研究中为了简化计算过程，仅取单个换热钻孔为研究对象，并做如下假设:将地埋管换热器周围的岩土层看作一个均匀介质的水平地层，并忽略地下水流动；同时忽略空气温度以及大地表面温度随季节的波动；并认为通过整个地层的大地热流是均匀的；管内流体介质的流动和传热采用一维模型，忽略流道横截面上的循环介质的速度和温度分布。

基于上述假设，在柱坐标系下，岩土层的导热微分方程由式(1)表示为

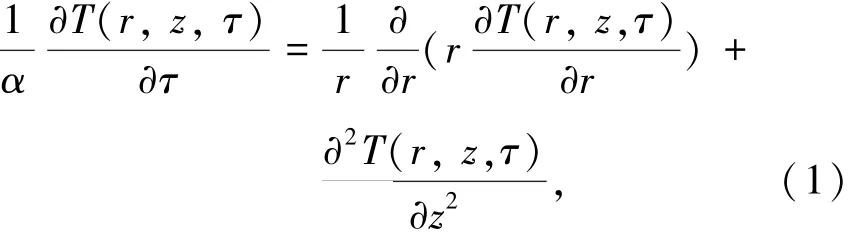
式中T(r，z，τ)为岩土温度，℃；τ为时间变量，s；α为热扩散率，m2/s。

流动方式为外进内出(从两管的夹层中向下流入，流体从外管流出)时，内管流体的能量方程由式(2)表示为

式中C为循环液的热容量，J/(s·K)；C1为热流外通道单位长度的热容量，包括循环液、外管壁和回填料的热容量，J/(s·K·m)；C2为热流内通道单位长度的热容量，J/(s·K·m)；R1为外管内循环液和钻孔壁之间的热阻，R2为内外管循环液之间的热阻，(m·K)/W；Tb(z)为钻孔壁温度，℃。

地温梯度由大地热流而产生。大地热流是指单位面积单位时间内由地球内部传输至地表而散发出去的热流，该数值通常由测定的地温梯度和岩土热导率两个参数间接计算得到[17]。岩土中的初始温度在径向分布上可近似认为是均匀的；在深度方向，由于地球内部的自下而上的大地热流的流动而产生纵向温度梯度。为简化计算，通常认为大地热流是均匀恒定的，岩土层中的初始温度由式(4)表示为

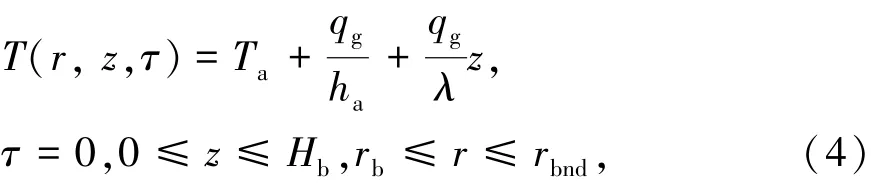
式中λ为岩土体平均导热系数，W/(m·K)；qg为大地热流，W/m2；rb为钻孔半径，m。

采用数值计算方法分析地埋管中的循环水从岩土中取热的问题，需要设定求解区域的边界。区域的下边界可设定在远离钻孔底部、岩土温度近似无扰动的位置。在计算中，取钻孔底部以下200 m的位置设定为等温边界条件，温度为岩土初始温度。同样，在径向方向取rbnd=205.76 m的位置定为等温边界条件。模拟结果证明，对于以10年为周期的模拟，这个边界范围也是足够大的。在地表的边界上设定为第三类边界条件，并假设地表以上的空气温度及表面传热换热系数始终保持不变，由式(5)表示为

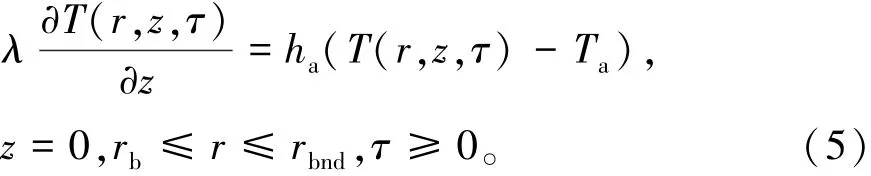
1.2 有限差分法求解传热模型

利用有限差分法可以对中深层地埋管传热区域进行离散，将上述传热微分方程组离散后得到差分方程组，并可采用“追赶法”求解。追赶法的基本思想与三角分解法、高斯(Gause)消去法相同，但计算公式更为简化，计算效率得以提高。

数值模型采用二维传热模型。对于二维的问题，采用朝后差分格式得到的节点方程中，通常有5个未知数，无法运用追赶法直接求解。若在两步连续时间步长中改变朝前和朝后差分的顺序，可使得节点方程中的未知数保持在3个以内，此时即可运用追赶法进行求解，得到钻孔内流体及岩土层的温度。对比该数值模型输出的温度与地热能开发利用模拟软件OGS(OpenGeoSys)输出的温度，经验证该数值模型具有较高的精确度，详细的模型对比和节点方程组参见文献[3]。

2 逆向传热区域及取热损耗率

2.1 中深层地埋管换热器逆向传热现象

选取工程上比较典型的中深层地埋管换热器作为研究对象，其基本设计参数见表1。假设一个供暖季连续取热天数为120 d，每天运行24 h，进口水温为20℃。

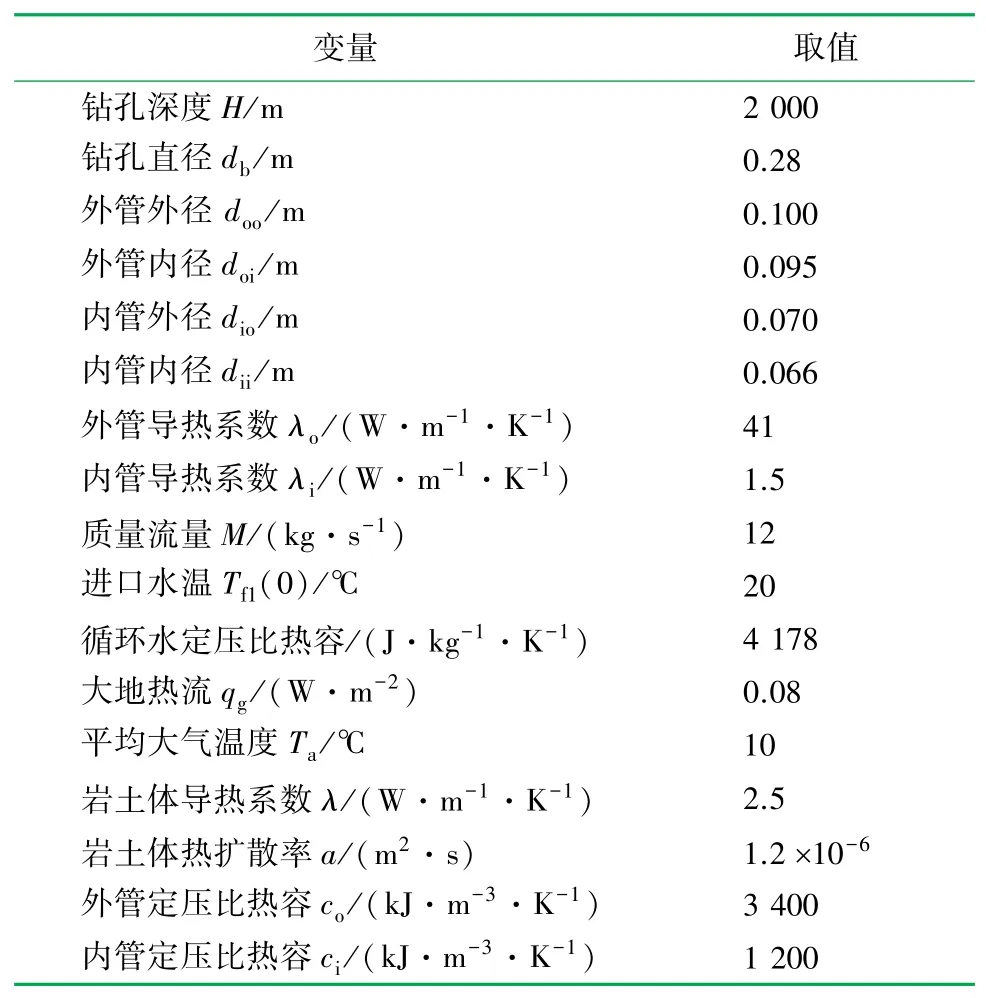
表1 基本工况参数表

根据上述数学模型可以计算出埋管周围岩土体在不同时刻、不同位置的温度响应。地埋管未取热前，岩土体初始温度分布云图和系统运行两个供暖季后地埋管周围岩土温度分布如图2所示。

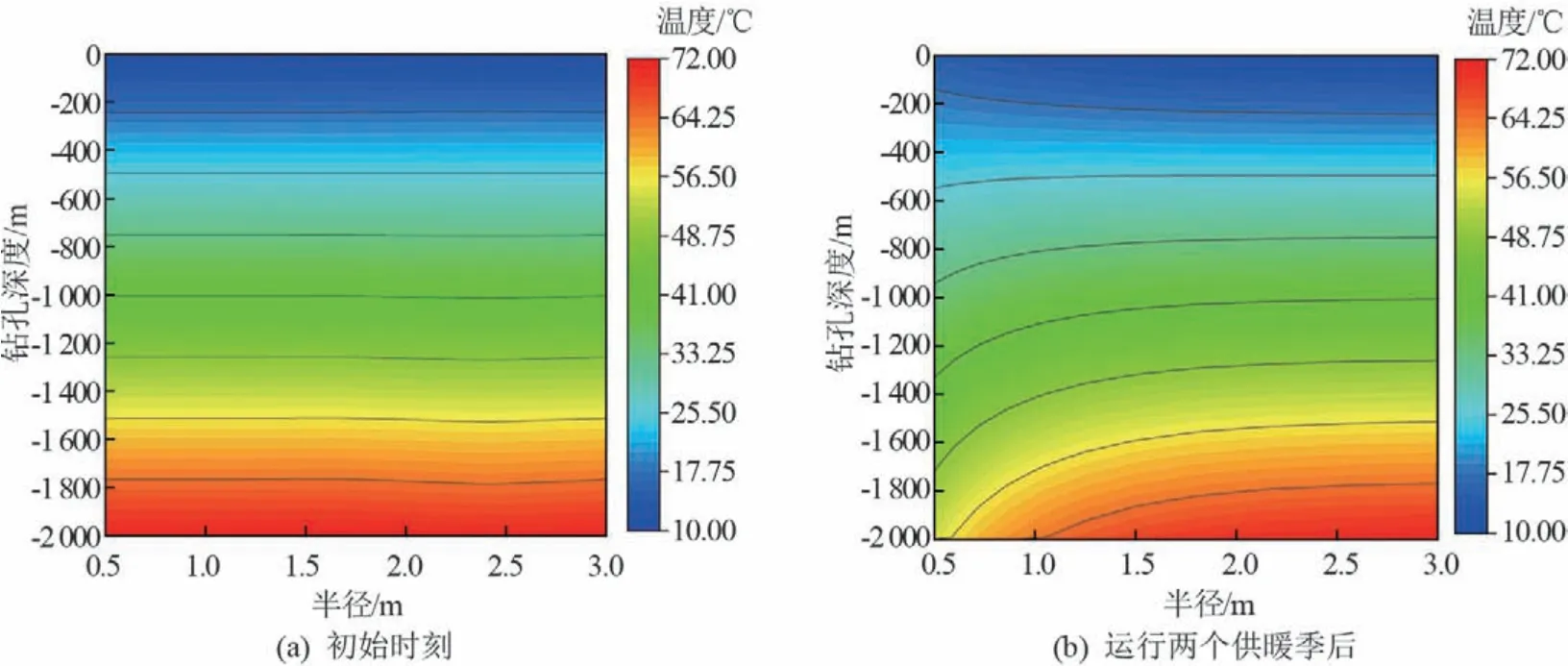
图2 地埋管周围岩土层温度分布云图

可以看到，距离埋管越近，岩土温度变化越大，但沿着半径方向最终趋于平稳，接近于岩土初始温度。如图2(b)所示，在浅层埋管区，呈现钻孔附近岩土温度明显高于远端岩土温度的现象，这是由于从深层岩土区返回的循环水温高于周边岩土温度，出现循环水加热岩土而产生的逆向传热现象。

取热时长为两个供暖季，流体温度以及不同半径处岩土温度在深度方向的变化曲线如图3所示。通过流体温度及周边岩土体在纵向的变化曲线，可以明显地发现，浅层埋管区存在由流体向岩土传热的现象。以文章选取案例的计算结果分析可知，此时逆向传热区域的深度高达326.5 m。

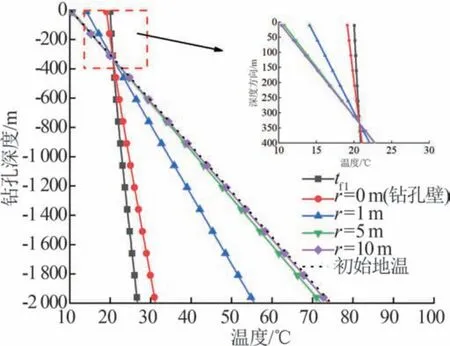
图3 流体及岩土温度沿深度方向变化趋势图

2.2 中深层地埋管换热器取热损耗率

在换热器的取热工况下，当存在逆向传热现象时，在一定深度范围内流体向岩土传热。这部分由流体传向岩土的热量显然是不利于地埋管换热器取热的。逆向传热量对整个埋管的换热的影响，可以用地埋管的取热损耗率φ来表示，其计算公式由式(6)表示为

式中ΔQ为在取热工况下流体向岩土传热造成的热损失量，kW；Q为实际取热量，kW。

同理，在蓄热工况下，深层土壤向流体的传热也是不利于蓄热的，同样也可计算出蓄热工况下的取热损耗率。

3 逆向传热现象影响因素分析

3.1 运行时间对逆向传热现象的影响

地埋管持续取热时间是影响地埋管换热器可持续运行及换热性能的一个重要参数。利用数值模型计算得到了第1、2、5个供暖季内逆向传热深度随时间的变化趋势，结果如图4所示。在供暖季的初始阶段，逆向传热深度随取热时间迅速减小，400 h以后基本趋于平稳达到准稳定状态。除此之外还可以发现，运行年数对逆向传热深度的影响较小，第1个供暖季达到准稳定后的逆向传热深度为326.91 m，而第2、5个供暖季内稳定后的逆向传热深度分别为326.51、326.04 m。分析原因可知，当一个供暖季的地埋管累计取热量较小时，地埋管换热器可以在系统间歇期通过周边岩土热量的补给近似恢复到系统运行初期状态。此工况下，每个供暖季的逆向传热深度基本一致。因此，运行时间对逆向传热区域的影响可以忽略不计。在以下分析所采用的时刻均为第2个供暖季结束时的时刻，其余基本工况参数见表1。

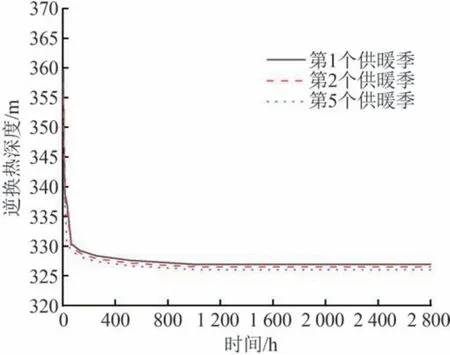
图4 逆向传热深度随时间的变化趋势图

3.2 流体温度对逆向传热现象的影响

地埋管侧流体进口温度会直接影响到外管温度与岩土层温度的相对大小，因此也决定了逆向传热区的深度以及埋管的总取热量。取热量、逆向传热深度、取热损耗率随进口温度的变化曲线如图5所示。随着进口水温的增加，取热量呈线性减小，逆向传热区深度与取热损耗率则随着进口水温的增加而增加。由计算可知，进口温度为10.00℃时，逆向传热现象消失，取热损耗率为0.00%。当进口温度为15.00℃时，浅层逆向传热区深度为165.32 m，由此导致的取热损耗率＜1.01%。这是由于在基本参数的设置中，环境温度为10.00℃，浅层地表温度约为10.00℃。由此可知，循环液进口温度的大小直接决定了逆向传热现象的存在与否，当进口水温小于当地地表环境年平均气温时，逆向传热现象可以忽略不计。因此，从地埋管的取热性能来看，循环液进口温度不宜高于地表环境年平均温度。

但是从热泵机组性能角度分析，过低的进口水温将导致较低的热泵机组能效。因此对于某一设计工况的中深层地埋管地源热泵系统，应进行综合性经济分析，选取最具经济性的循环液进口温度。

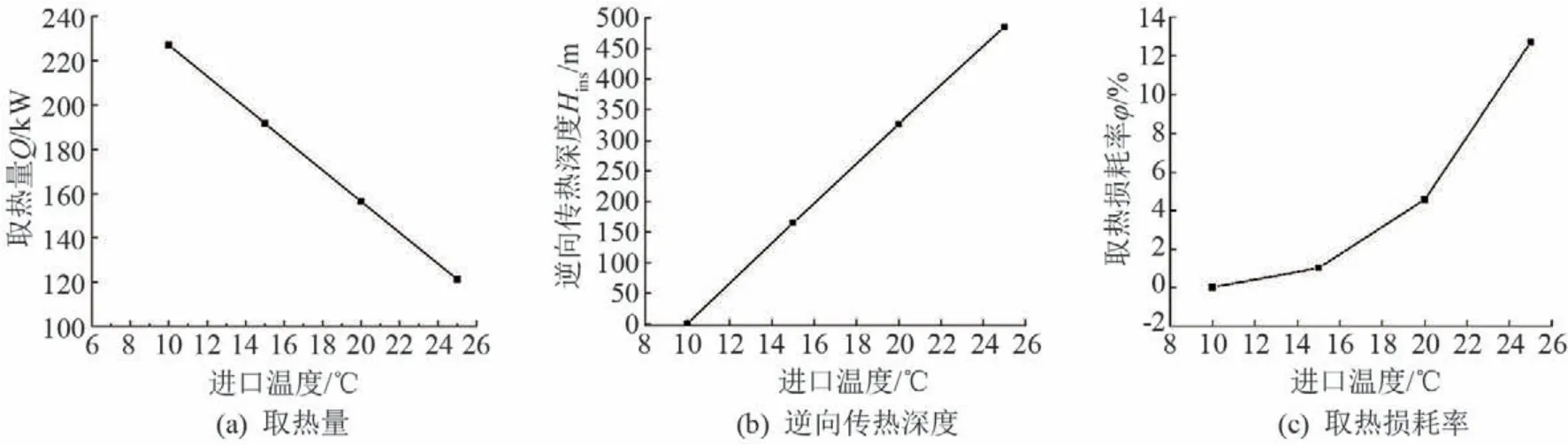
图5 循环液进口温度对逆向传热的影响

3.3 大地热流对逆向传热现象的影响

地下岩土层的初始温度也影响着逆向换热区的深度、取热量以及取热损耗率。岩土层的初始温度主要取决于大地热流，在大地热流较大的地方，地下岩土层的温度较高，地热能资源更为丰富。充分了解大地热流对取热量、逆向传热区深度、取热损耗率的影响有利于合理调控各运行参数，从而提高热泵机组及地埋管换热器的运行效率。

当进口温度为20℃时，取热量、逆向传热区深、取热损耗率随大地热流的变化曲线如图6所示。随着大地热流的增加，取热量呈线性增加，而逆向传热深度与取热损耗率则逐渐降低。当大地热流从0.04 W/m2增加到0.10 W/m2时，逆向传热区深度减少了301.60 m，取热损耗率减少了13.23%。对于大地热流较大的区域，在其他设计参数不变的情况下，可以适当的提升循环液设计温度，以提高热泵机组的性能。

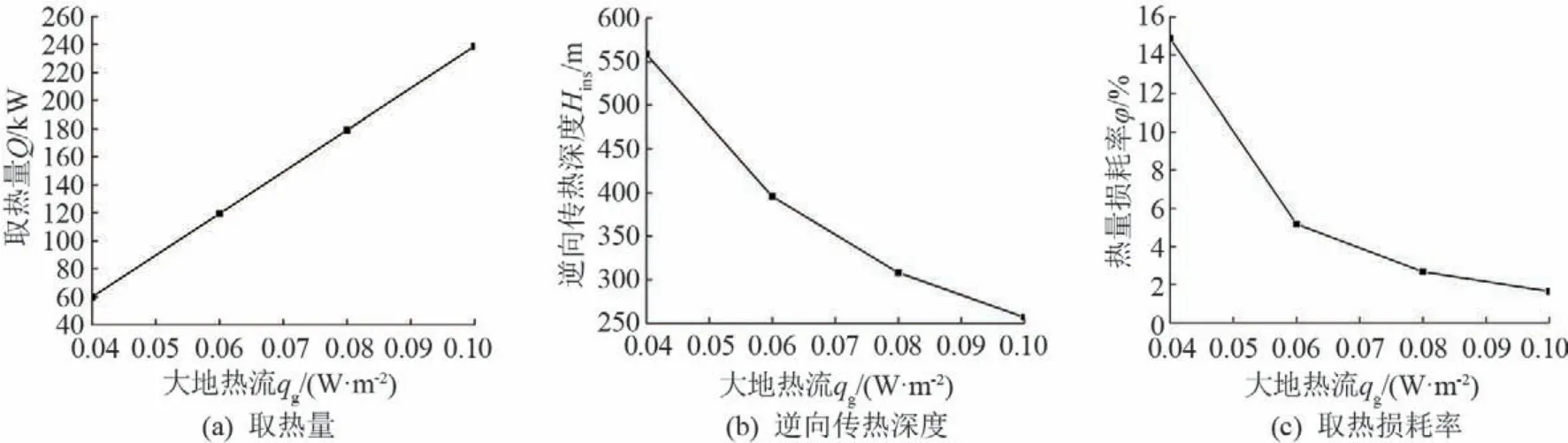
图6 大地热流对逆向传热的影响

3.4 循环液流量对逆向传热现象的影响

循环液的流量直接影响整个地埋管换热器的运行效率，同时也影响着逆向传热区的深度。埋管取热量、逆向传热深度以及取热损耗率随循环液质量流量的变化曲线如图7所示。随着循环液流量的增加，取热量增加，逆向传热区的深度及取热损耗率逐渐减小。这主要是由于增大循环液流量，在进出口截面积不变的情况下流速增加，进而提高了循环液与周围岩土的传热系数；同时流量增大，进出口循环液的水温将有所降低，因此降低了逆向传热区深度以及热量的损耗率。

在实际工程中，循环液的设计流量受多个参数的影响，如设计的热负荷、机组的进出口温差以及水泵的能耗与系统的综合能效等。其中，水泵输送能耗的关键因素取决于循环液的流量。质量流量对循环水泵能耗的影响如图8所示，随着质量流量的增加，取热量与水泵耗功都呈现增加的趋势。增加质量流量显然有利于地埋管换热器的运行，但是增加流速的同时，也增加了水泵的能耗。因此，在工程上设计循环液流量时，应将循环水泵的输送能耗考虑在内。

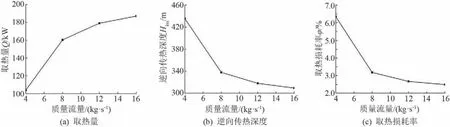
图7 循环液质量流量对逆向传热影响

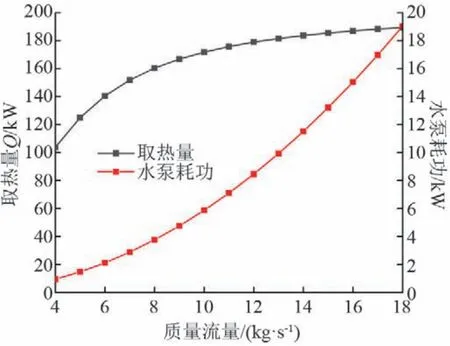
图8 质量流量对循环水泵能耗的影响

3.5 岩土导热系数对逆向传热现象的影响

岩土层的导热系数也影响到逆换热区的深度。逆换热区的深度随岩土导热系数的变化曲线如图9所示，可以看到，随着岩土导热系数的增加，逆换热区的深度也呈线性增加。当岩土导热系数为1.5 W/(m·K)时，逆换热区深度为205.9 m；当岩土层导热系数增加到3.5 W/(m·K)，逆换热区的深度增加到454.5 m。在岩土导热系数高的地方使用中深层地埋管换热器要适当增加保温层的厚度。

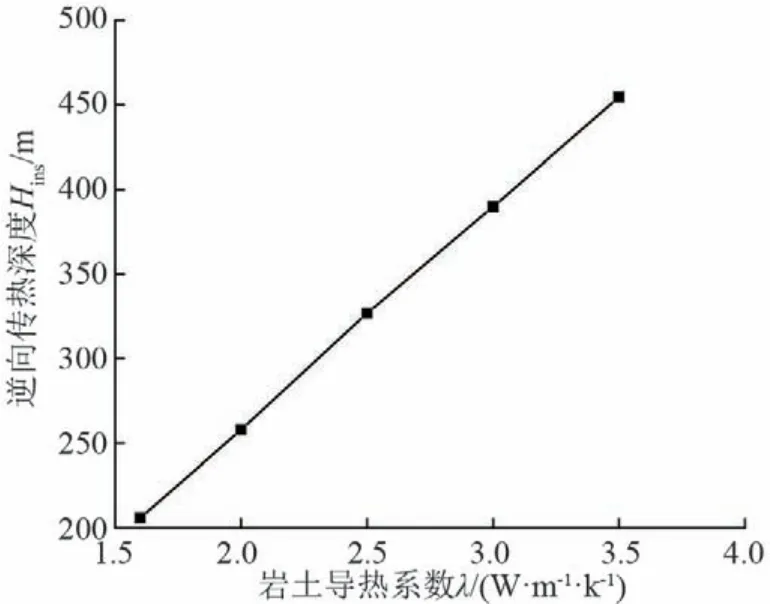
图9 逆换热区深度随岩土导热系数的变化趋势图

3.6 保温层对换热器性能的影响

当循环液的温度大于周围岩土温度时，循环液从底层岩土携带的热量会在岩土层上部较冷的部分消耗，而逆向传热区的深度与总取热量取决于循环液和周围岩土之间的温差。设置保温层可减少热量损失率，取热与放热工况下保温层深度对热损耗率的影响如图10所示。取热工况下，随着保温层深度的增加，损耗率逐渐减小，当保温层为100 m时，取热损耗率由2.67%降到2.19%。在放热工况下，随着保温层深度的增加，放热损耗率也在逐渐减小，当保温层为100 m时，放热损耗率由1.79%降低到0.44%。

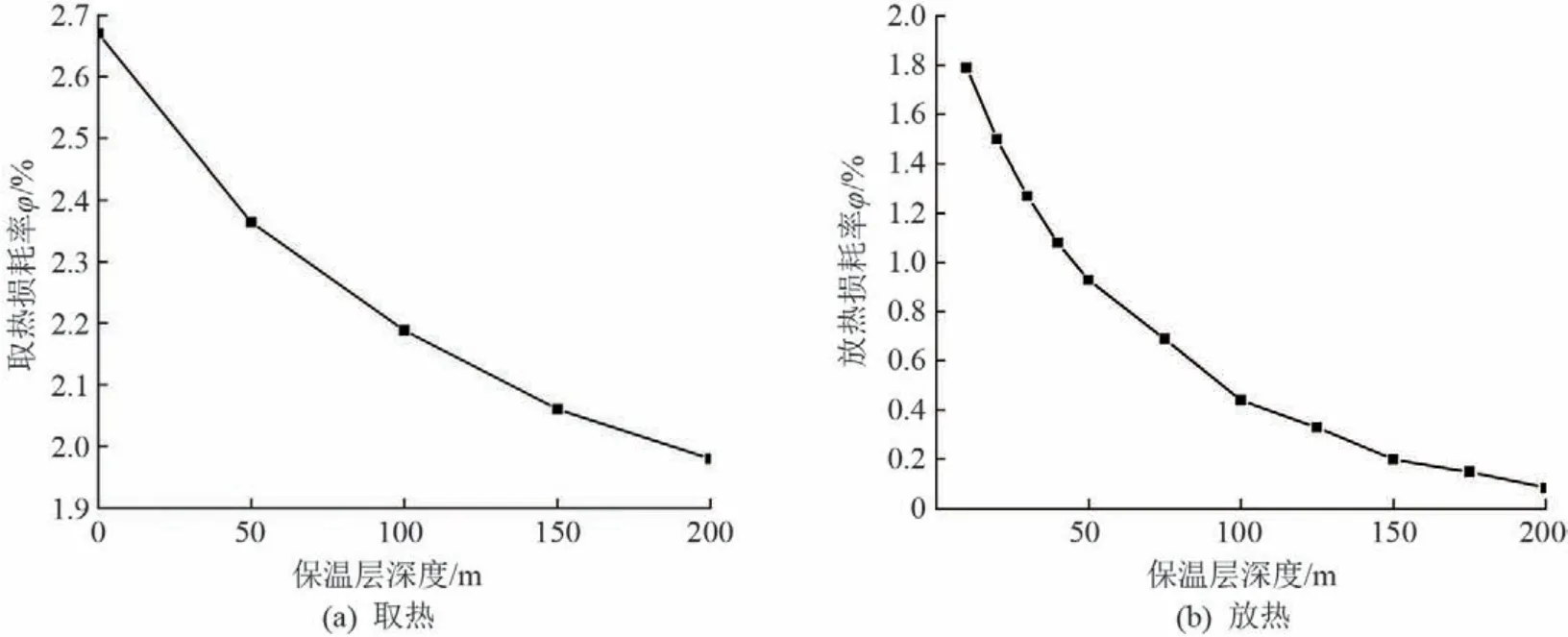
图10 取热与放热工况下保温层深度对热损耗率的影响

3.7 逆向传热深度拟合公式

由上述分析可知，逆向传热区的深度随着质量流量及大地热流的增加而减小，随循环液进口温度的增加以及岩土导热系数的增加而增加，逆向传热区深度与进口温度以及岩土导热系数基本呈线性变化关系。

为了使计算结果更有利于工程应用，可将逆向传热区深度Hins拟合为与M、qg、Tf1、λ等变量相关的函数，其拟合公式由式(7)表示为

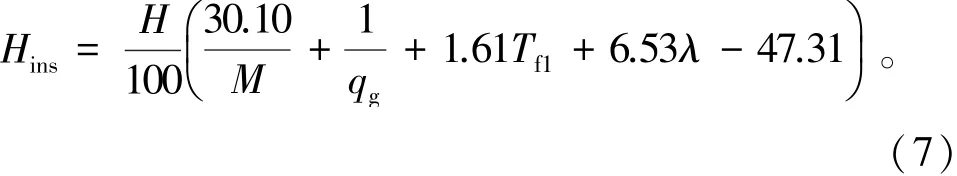
在拟合过程中，各参数的取值范围如下:质量流量M为4～20 kg/s，qg为0.03～0.12 W/m2，循环液进口温度Tf1为10～25℃，岩土导热系数λ为1.0～3.5 W/(m·k)。在各参数的取值范围内，拟合公式的R2为0.97，拟合相关性较高，可用于快速估算不同工况下的逆向传热区深度。

为了验证所得拟合公式的正确性和合理性，将数值模型与拟合公式计算所得的数据进行验证，并取大地热流作为模型对比的变量，如图11所示。可以看到，拟合公式所得的数据与数值模型所得的数据具有较好的拟合度，当大地热流为0.12 W/m2时误差最大，但也仅达到2.98%。当其他参数M、Tf1、λ变化时，其最大误差分别为0.51%、5.15%、5.83%。

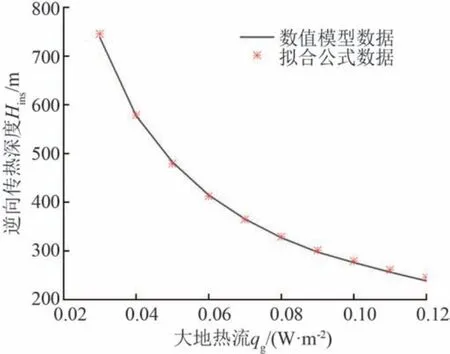
图11 数值模拟数据与拟合公式数据对比

4 结论

针对中深层地埋管换热器取热问题，根据建立的中深层地埋管换热器数值传热模型，获得了地下岩土温度及循环液温度的变化趋势，进一步计算得到了逆向传热区深度，并分析了运行时间、循环液温度、大地热流、循环液质量流量等参数对逆向传热区深度以及取热损耗率的影响。主要结论如下:

(1)为保持地埋管换热器达到最大取热量，循环液进口温度设计应偏低，在模拟工况下建议进口温度选为10℃，即等于地表环境温度。此时，逆换热现象消失，取热损耗率为0.0%。

(2)地埋管总取热量随着大地热流以及循环液质量流量的增加而增加，对应的逆向传热深度与取热损耗率则逐渐降低，当循环液进口温度为20℃，大地热流从0.04 W/m2增加到0.1 W/m2时，逆向传热深度减小301.60 m，取热损耗率降低13.23%。

(3)根据模拟结果，给出了适用于工程设计用的逆向传热深度拟合计算公式，主要考虑了影响逆向传热深度的关键变量。在各变量的取值范围内，拟合公式的R2为0.97，所得数据与数值模型数据的最大误差为5.83%。