基于像素值分类的脉冲噪声检测与恢复算法
雷继海
(陇东学院电气工程学院,甘肃 庆阳 745000)
0 引言
图像在获取、传输以及存储过程中,极易受到外界噪声干扰,造成图像视觉质量下降,严重时甚至可能导致图像中某些重要信息丢失,给图像的后续处理带来极大不便。其中,脉冲噪声较为普遍[1]。传统的处理方法是采用中值滤波算法对其进行消除,但是存在很多弊端。为了弥补传统中值滤波算法的不足之处,学者们又相继提出了基于加权方法的各类中值滤波算法,并不断对其改进,以期对滤波结果进行优化[2-4]。这些算法虽然取得了较好的滤波效果,但是在滤波时并没有对噪声点与非噪声点进行有效区分,在处理噪声点的同时,对非噪声点也进行了一定程度的处理,使得处理后的图像变得模糊。
针对上述算法对噪声点与非噪声点整体处理的不足,学者们又提出了先实现噪声检测而后进行噪声剔除方案。其中具有代表性的方法有极值中值滤波(extremum median filtering,EMF)、开关中值滤波(switching median filtering,SMF)以及相应的改进算法等[5-11]。这些方法极大地改善了滤波性能,较为完整地保留了滤波后图像的细节信息。但是较高密度的噪声在剔除噪声点后,往往会出现加大面积的空缺,无法较为精准地对噪声点进行恢复,滤波能力显得不足。
对于高密度噪声的处理,当前普遍的做法是采用各种结构较为复杂的算法,包括自适应中值滤波(adaptive median filtering,AMF)、基于小波变换的算法、决策算法以及当前研究较为集中的基于深度学习的各类算法等[12-17]。这些算法的提出与应用,对图像噪声的处理产生了极大影响,使得噪声的处理效果有了很大提升。但是这些算法在处理含有噪声的图像时,对参数设置的依赖性较大,不同的参数会对滤波结果产生不同影响。
结合上述脉冲噪声检测与恢复方法的不足,本文提出了一种基于像素值分类的脉冲噪声检测与恢复算法。该算法根据图像中脉冲噪声的特点,以像素值为0或255的点为中心点选取滤波窗口,对滤波窗口中的像素点进行精确分类,并对分类后的像素点采用不同的处理方法进行噪声检测与恢复,以期达到较为理想的处理结果。
1 脉冲噪声模型
在一幅数字化图像中,脉冲噪声总是数字化为极值(纯黑或纯白)。由于这一结果,负脉冲以一个黑点出现在图像中,正脉冲以一个白点出现在图像中。对于一个8位图像而言,意味着脉冲噪声为0或255。令S为不含噪声的原始图像、Y为带有脉冲噪声的图像,则脉冲噪声的数学模型可表示为:
Yij={0,Pa255,PbSij,1-(Pa+Pb)}
(1)
式中:Yij为脉冲噪声图像Y在(i,j)点的像素值;Sij为不含噪声的原始图像S在(i,j)点的像素值;Pa为含噪图像中负脉冲噪声出现的概率;Pb为正脉冲噪声出现的概率。
2 基于像素值分类的噪声检测与恢复算法
2.1 算法描述
使用传统均值滤波时,窗口大小的选取直接影响图像边缘以及细节信息。本文对均值滤波算法进行了改进,利用了如图1所示的滤波窗口结构,选取绝对差最小的两个点的均值与待处理点进行运算,得到均值滤波结果。基于像素值分类的噪声检测与恢复滤波(based on pixel value classification filtering,BPVCF)是从脉冲噪声像素值为0或255这一特点出发,假设原始图像中像素值为0或255的像素点全为噪声点,以噪声点为中心设计滤波窗口,对窗口内的各点进行分类;依据分类结果对窗口中像素值为0或255的点作进一步判断,得到噪声点与可疑噪声点;剔除噪声点,保留非噪声点与可疑噪声点;依据窗口中剩余像素点的数目,采用不同方法进行噪声恢复。对于原始图像中像素值在0到255之间的像素点,不认为其是噪声点且不作处理,保留原始像素值。算法具体过程如下。

图1 滤波窗口结构示意图
假设F=[p(i,j)]是以像素p(i,j)组成的、大小为m×n的含有脉冲噪声的原始图像。其中,i和j的范围为1~m和1~n,0≤p(i,j)≤255。
①对于所有的i和j,如果p(i,j)=0或255,以该点为中心选取3×3的滤波窗口,对窗口内的像素点作如下分类并处理。
第一类:若滤波窗口中除中心点外,剩余点像素值满足(0 第二类:若滤波窗口中除中心点外,剩余点像素值满足(240 第三类:若滤波窗口中除中心点外,剩余点像素值满足(10≤p≤240)≠Ø,则认为窗口中像素值为0和255的点为噪声点。选取窗口中像素值10≤p≤240的点参与噪声恢复运算。此时,当选取点的个数不少于3个时,以所选点作中值滤波运算,以中值滤波结果M替换中心点像素值。当选取点的个数为1时,直接以该点像素值替换中心点像素值;当选取点的个数为2时,以这两点平均值替换中心点像素值。 第四类:若窗口中所有点的像素值为0或255时,无法对中心点作出有效判断,将3×3滤波窗口扩大到5×5,再对该窗口内的所有点按照第一类和第二类进行判断恢复。若滤波窗口扩大到5×5时,仍满足窗口中所有点的像素值为0或255,则将滤波窗口扩大到7×7,再依次按照第一类和第二类进行判断恢复。若此时所有点的像素值仍为0或255,则直接选取窗口中重复次数较多的像素值为0或255点直接替换中心点像素值。 ②移动滤波窗口,重复步骤①。 ③输出滤波后的图像。 为了对上述算法中提到的四类情况进行详细说明,采用以具体像素值为例的噪声恢复过程示例,分别对2.1节步骤①中对应的四种分类结果下的噪声恢复进行描述。 ①假设第一类情况下滤波窗口内像素值分布如图2所示。 图2 第一类情况下滤波窗口内像素值分布图 对于图2(a)和图2(b)而言,既含有像素值0 对于图3中(a)所剩像素点采用中值处理,其结果M=3;图3(b)中由于只剩下两个点,求其平均值A=2;图3(c)中只剩下一点,直接取值为4。以计算结果对中心点噪声进行恢复。第一类情况下,噪声恢复结果如图4所示。 图3 剔除后剩余的像素点 图4 第一类情况下噪声恢复结果 算法中第二类与第一类处理类似,故不在此赘述。 ②假设第三类情况下滤波窗口内像素值分布如图5所示。 图5 第三类情况下滤波窗口内像素值分布图 根据第三类处理过程,选取窗口中除中心点外的像素点求取中值,其结果为M=82。以此结果替换中心点像素值,第三类情况下噪声恢复结果如图6所示。 图6 第三类情况下噪声恢复结果 ③假设第四类情况下滤波窗口内像素值分布如图7所示。 图7 第四类情况下滤波窗口内像素值分布 根据算法中的第四类处理过程,此时应将3×3滤波窗口扩大到5×5。假设扩大窗口后的像素点分布如图8所示。 扩充后的像素值分布满足第三类条件,选取窗口中像素值为10≤p≤240的点进行中值运算,其结果为M=112。以此结果替换中心点像素值,噪声恢复结果如图9所示。 图9 第四类情况下噪声恢复结果 为了对本文提出算法的性能进行评估,从Matlab7.0的toolbox文件夹中的images文件下的imdemos选取了onion图像作为标准测试图像,分别添加密度为40%和60%的脉冲噪声。以AMF[18]、EMF[19]、SMF[20]以及BPVCF进行处理,对比了不同方法处理后图像的视觉效果。40%和60%噪声密度下,滤波结果分别如图10、图11所示。 图10 40%噪声密度下滤波结果 图11 60%噪声密度下滤波结果 由图10可知,在脉冲噪声密度为40%情况下,图10(d)和图10(e)均未能将噪声完全滤除,滤波效果较差;从总体上来看,图10(c)和图10(f)效果差别不大,但是仔细观察就会发现,图10(c)中存在图像边缘模糊现象,视觉效果较之本文算法差。由图11可知,在脉冲噪声密度为60%情况下时,这一现象更加明显。综上所述,本文BPVCF算法在视觉效果上要优于EMF、SMF和AMF。 为了能够从定量计算结果上全面、真实地反映EMF、SMF、AMF和本文算法在不同图像、不同噪声密度下的处理效果,分别采用了峰值信噪比(peak sigmal-to-noise ratio,PSNR)、平均结构相似性(mean structural similarity,MSSIM)和图像增强因子(image enhancement factor,IEF)对处理后的图像进行评价[21-22]。其中,PSNR、MSSIM和IEF计算公式分别如式(2)~式(5)所示。 (2) IS(p,q)=lα(p,q)×cβ(p,q)×sλ(p,q) (3) (4) (5) 计算上述三个参量时,从Matlab7.0的toolbox文件夹中的images文件下的imdemos选取了onion、cameraman、pout、coins四幅图像作为标准测试图像。对测试图像分别添加密度为10%~90%的脉冲噪声,并针对每幅测试图像,分别采用EMF、SMF、AMF和本文BPVCF算法进行处理。处理结果表明,本文算法处理后的PSNR、MSSIM及IEF值均优于其他三种算法。以测试图像中pout处理结果为例,得到了经不同算法处理后图像的PSNR、MSSIM以及IEF与噪声浓度关系,如图12所示。 图12 PSNR、MSSIM以及IEF值分别与噪声浓度的依赖关系 由图12可以看出:在噪声密度低于80%时,本文算法的性能优于其他算法;但是当噪声密度大于80%时,本文算法处理后的PSNR和IEF值略低于AMF算法而高于EMF和SMF算法,但MSSIM值优于AMF算法。由此表明,在处理高密度噪声时,本文算法也具有与AMF算法相当的处理效果。 本文针对含有脉冲噪声的图像,提出了一种基于像素值分类的脉冲噪声检测与恢复算法。试验结果表明,该算法对于脉冲噪声密度低于80%的图像有很好的处理效果,处理后图像的PSNR、MSSIM和IEF值以及视觉效果优势明显。在处理噪声密度高达80%以上的图像时,其处理效果也与AMF算法相当。2.2 处理示例
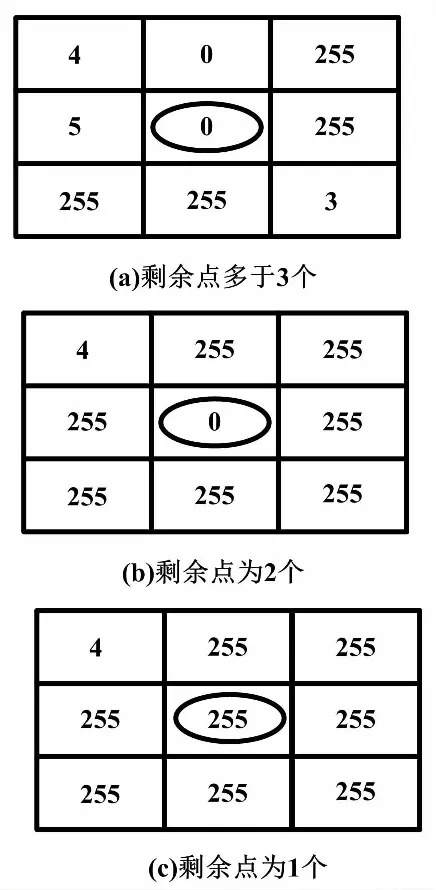
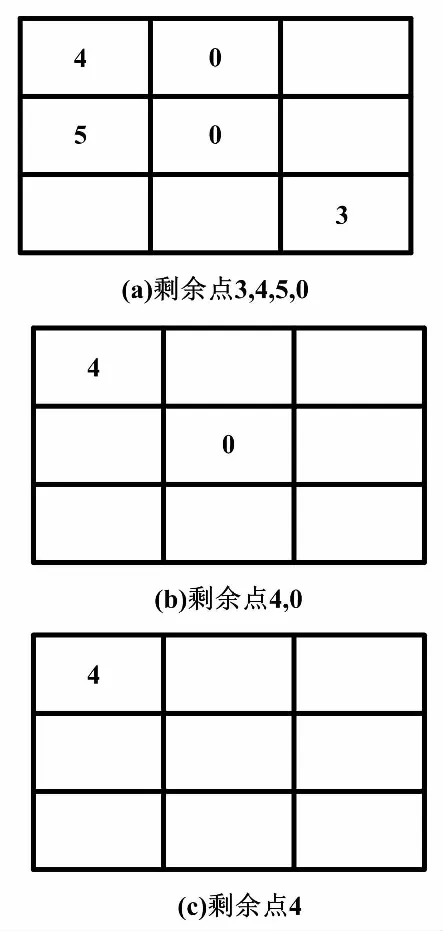

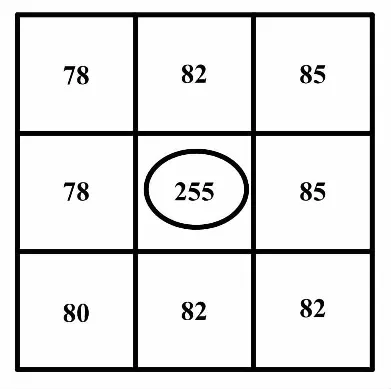
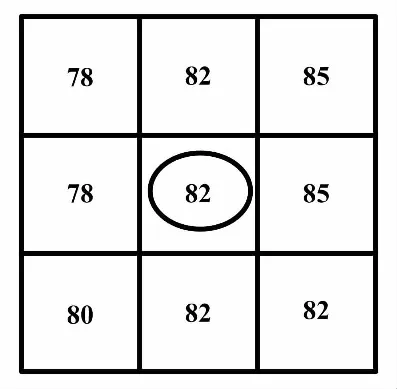
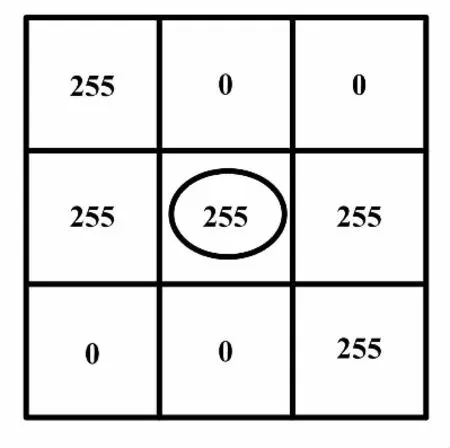
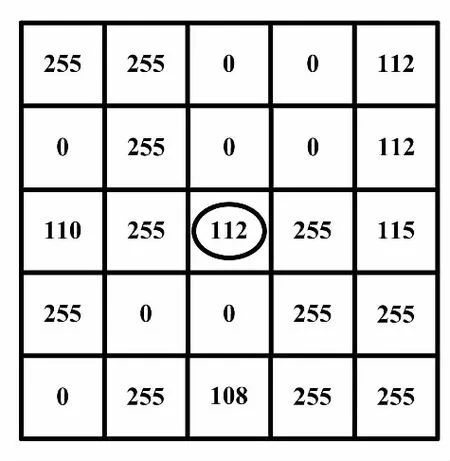
3 试验结果与分析




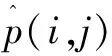
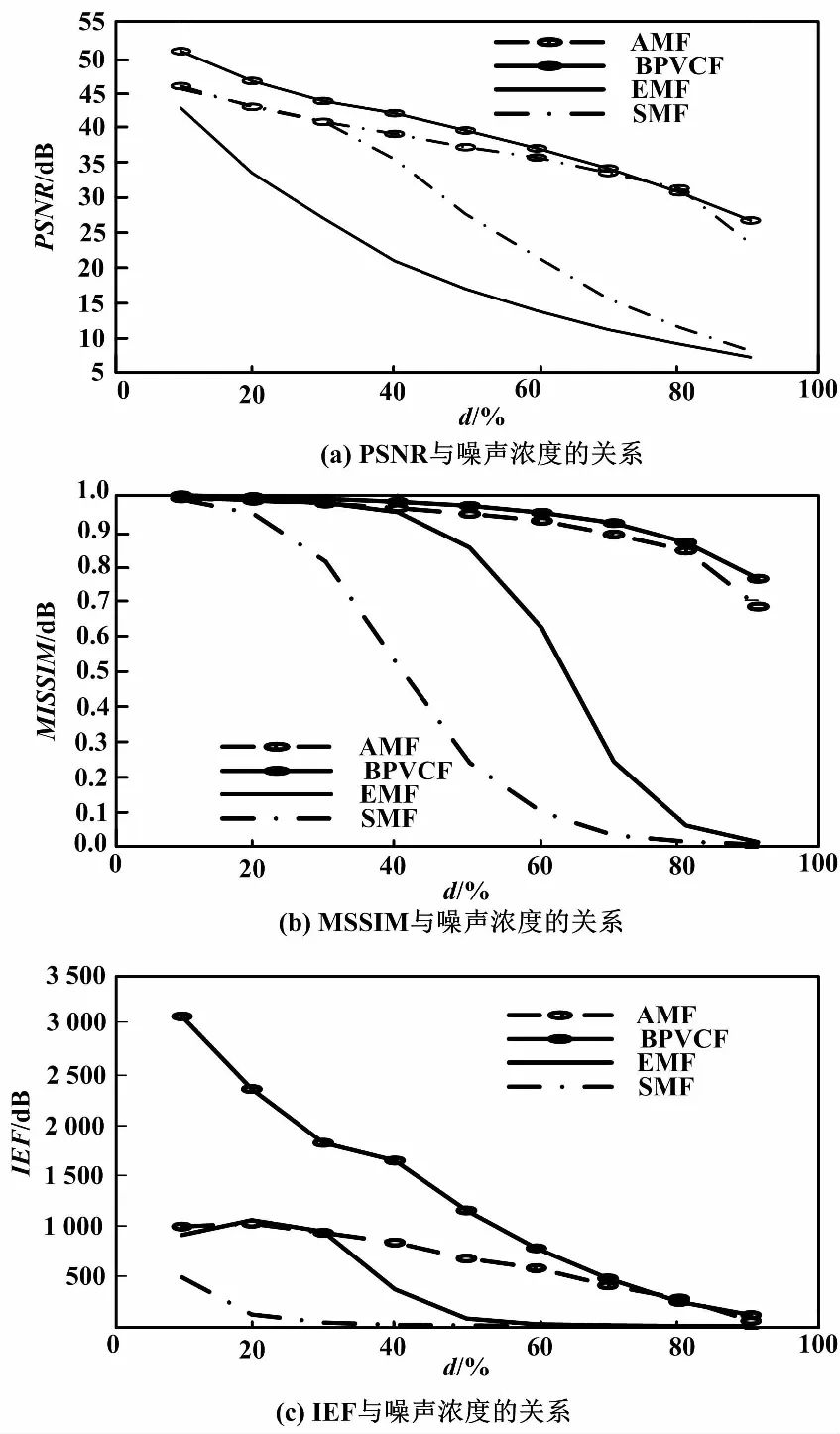
4 结论

