基于地势拟合的三维层析方法研究

薛 骐

(中国铁路设计集团有限公司，天津 300251)

GPS 气象学是利用GPS 理论监测气候变化，测量大气水汽含量，并对气象学理论进行研究的方法[1]。基于大气层时产生的延迟量和偏折数据，使用GPS 卫星信号精确计算大气水汽的相关数据指标，通过这种方法反演出来的大气水汽精度可达毫米级，与探空手段精度相当。 在20 世纪90 年代，利用GPS 反演大气水汽方法开始快速发展，成为一种大气探测手段[2-3]。C.Champollion 等利用三维层析方法对水汽输送变化进行了分析，并在不同高度上绘制了大气可降水量的密度廓线[4-5]。 Miidla 对现有三维层析方法进行了概述，在此基础上开发了AWATOS，用于在空间三维上对大气可降水量进行研究[6]。 在前人研究的基础上，提出一种基于地势拟合的三位层析方法，并对其反演精度进行数据分析。

1 地基GPS 水汽反演基本原理

在GPS 信号穿越大气层时，会受到电离层、对流层以及折射等影响。 通过研究发现，这种延迟等同于GPS 信号传播路径的延长。 基于此，可对GPS 误差源进行研究，发现该延迟与信号传播路径上大气水汽含量成正比[7]。 延迟主要由电离层、对流层、卫星和接收机钟差等引起，其中电离层延迟可以通过使用双频技术进行消除，卫星和接收机钟差可以利用差分技术进行消除，对流层延迟则需要使用相关模型和算法的GPS 软件进行计算。 考虑到对大气水汽反演的实时性要求较高，使用PPP 精密单点定位的方法进行计算，使用Automatic Precise Positioning Service 软件进行对流层相关计算[8-9]。 该软件为JPL 提供，可解算天顶总延迟，并支持静、动态及近实时定位和精确定位4 种模式的在线解算。

1.1 天顶总延迟

GPS 卫星信号在传播过程中，受各种因素影响会发生折射弯曲和延迟。 其中，折射弯曲的影响较大，延迟量较小，这是由于大气折射造成的影响，这种影响需要进行消除。 在GPS 气象学研究过程中，主要就对流层的延迟进行研究，并进一步计算水汽相关内容。GPS 信号在对流层中的传播速度为v=c/n，其中n=c0/c。 n 为大气折射指数，则对流层总延迟ΔL 为[10-11]

式中，(S-G)代表因信号导致的路径增长部分，将对流层延迟沿高度积分，可得GPS 天顶方向总延迟，有

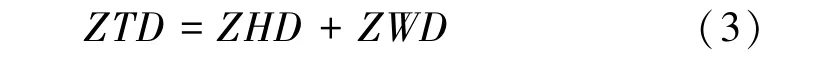
ZTD 为天顶总延迟，ZHD 为天顶静力延迟，ZWD为天顶方向湿延迟。

通过Automatic Precise Positoning Service(APPS)软件解算，可得到的天顶总延迟，通过计算发现，该软件动态定位中误差为0.16 m，静态定位结果中误差为1.2 cm，精度良好。 频率可达到30 s/次，能够作为本研究的解算软件。

1.2 天顶静力延迟

从前文中已经看出，GPS 卫星信号的传输过程是对大气折射率的积分过程，但是积分所需要的数据量很大，还包括影响大气折射的温度、气压和相对湿度等多种数据资料，然而，信号传播路径上的相关数据很难获取，只能通过测站位置的相关气象条件进行预测。因此，需要基于测站位置建立气象条件模型。 由于天顶湿延迟难以使用模型表述，目前多使用地表气象信息来进行计算[12-17]。 以下采用Saastamoinen 模型进行计算，有

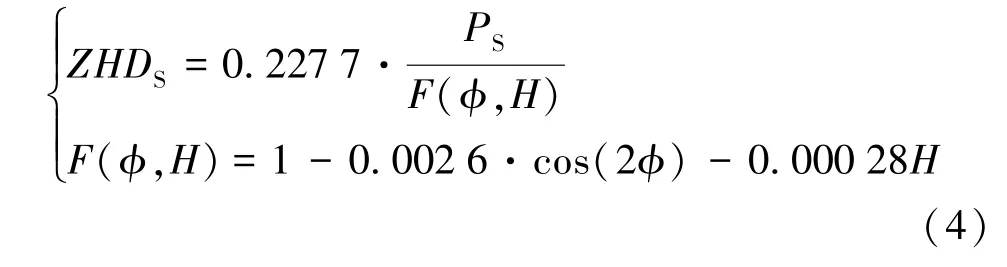
式(4)中，PS为地面气压，H 为测站海拔高度，φ为测站纬度。

1.3 天顶湿延迟及PWV 计算

天顶湿延迟与天顶干延迟共同组成天顶总延迟，对流层中天顶湿延迟沾总延迟的10%～20%。 受对流层运动影响，其变化迅速，难以用固定模型进行描述，故使用天顶总延迟ZTD 减去天顶干延迟ZHD 进行计算，然后再乘以转换系数，以Π 计算大气可降水量PWV。 天顶湿延迟ZWD 和大气可降水量PWV 表述公式为

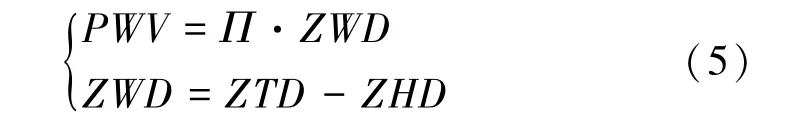
式(5)中，PWV 为大气可降水量，Π 为转换系数，ZWD 为天顶湿延迟，ZTD 为天顶总延迟，ZHD 为天顶干延迟。

1.4 斜路径水汽含量

在地基GPS 水汽反演测量过程中，使用的是地面测站到卫星之间的信号来计算斜路径上的水汽含量，同样，斜路径上的水汽也分为斜路径干延迟和湿延迟两种。 随着卫星高度角的下降，GPS 与地面测站之间信号的延迟路径会逐渐增加，该倾斜路径上的延迟和测站上空的天顶延迟可以建立相关的映射函数进行变换计算，故斜路径湿延迟SWD 可以利用ZWD 天顶湿延迟和相关映射函数进行计算。

目前，映射函数主要有GMF、Marini、NMF、Chao 和CFA2.2 几种，其中以NMF 和GMF 两种映射函数应用最为广泛，相较于其他几种模型，其精度、效率更高。而GMF 模型映射函数更加有利于编程实现，故使用GMF 映射函数。

2 基于地势拟合的三维层析基本原理与方法

三维层析技术源于医学上的CT(Computerized Topography)技术，即断层扫描技术。 使用该技术得到水汽分布的三维空间特征，得到的结果完全能够满足短临天气预报的要求。 利用三维层析技术，先根据GPS 解算得到各信号路径上的水汽值，再对各路径上的水汽含量进行积分，进而可在一段时间内得到多个观测方程，求解各个格网内的水汽结果。

GPS 格网划分需要满足:①仰角最低为10°，各测站之间的站间距＜60 km；②根据Flores 等的研究，GPS三维层析技术在垂直分层距离上最小距离为300 m，毕研盟认为最佳垂直方向的测站距离为800 m，本文使用的垂直分层距离为1 000 m，三维层析技术如图1。

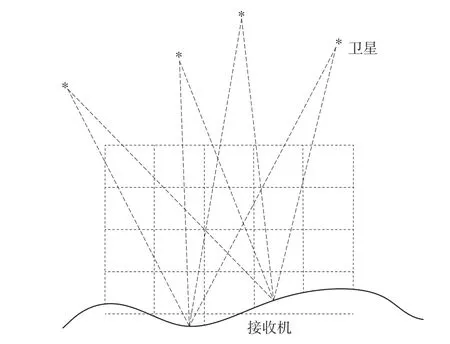
图1 三维层析方法示意

由图1 可知，先将GPS 观测网内空间分成单元格网，再将各个格网内的水汽密度看成均匀分布且固定的常量(5 min 和10 min 内)，则各路径上的水汽含量等于所穿过的各格网水汽之和，计算公式为

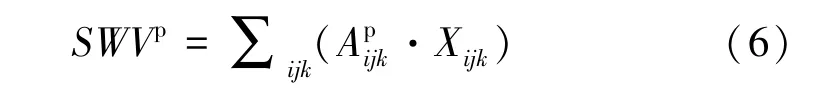
从上述分析可以看出，目前主要的研究内容是针对分层厚度、格网距离划分等，没有考虑平面格网的划分对测站处于不同层面的冲突性问题。 从图1 可以看出，未能将多个测站同时纳入第一层格网分布内，这可能会产生以下几种问题:①接收机由于海拔过高处于第二层格网范围内，导致卫星至该测站的信号不能解算第一层格网；②接收机处于第一层格网中间偏上的位置，这样对解算结果会造成很大的误差影响；③接收机由于海拔过低导致位于第一层格网以下，这样会导致一部分卫星至接收机的信号裸露在外，会造成数据解算质量大幅度下降。

基于地势拟合的三维层析方法是在传统层析方法上先确定合适的地势拟合模型，根据确定好的地势拟合模型进行三维层析。 但考虑当信号穿越拟合曲线上无法对刺穿位置进行确定的问题，将拟合曲面中的每个格网进行平面化，平面化的方法是根据每个格网内曲线的中心的坐标进行平面延长，这样就将信号与曲面的求解问题转换到信号与平面的交点求解问题，如图2 所示。

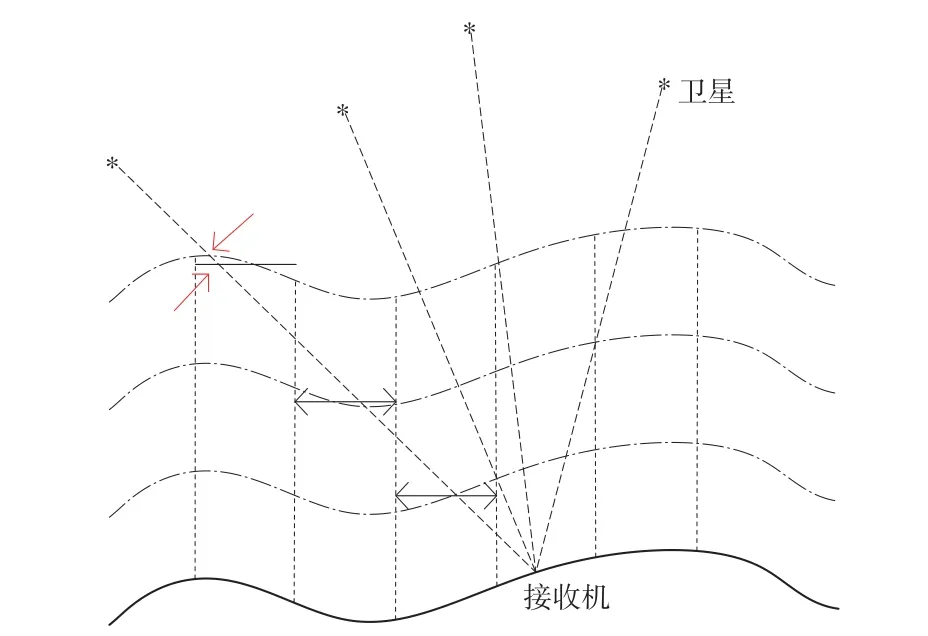
图2 基于地势拟合的三维层析方法示意

地势拟合方法可采用二次拟合H=a1+a2x2+a3x+a4y2+a5y 模型和三次拟合H=a1+a2x3+a3x2+a4x+a5y3+a6y2+a7y 模型，有关模型的论述见文献[7]，在此不再赘述。

实验数据使用中国香港地基GPS 网中11 个站的观测数据，分别为:HKFN(Fem ling)、HKKT(Kam Tin)、HKLT(Lam Tei)、HKMW(Mui Wo)、HKNP (Ngong Ping)、HKOH(Obelisk Hill)、HKPC(Peng Chau)、HKSL(Siu Lang Shui)、HKSS(Shap Sze Heung)、HKST(Sha Tin)、HKWS(Wong Shek)，数据见表1。

表1 中国香港各测站坐标数据

2.1 传统三维层析结果

图3 为传统三维层析方法在KHOH 测站上空解算的水汽密度与探空资料的比对。

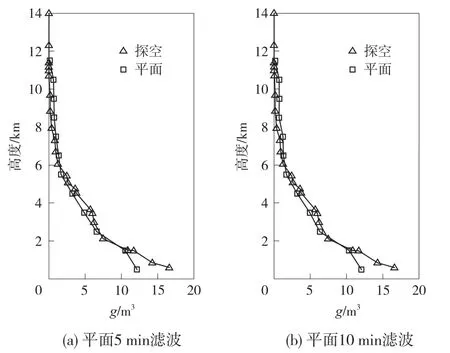
图3 传统层析方法

由图3 可知，传统层析方法总体结果与探空结果符合程度较好，但是没有考虑测站之间的高差问题导致数据质量较差。 根据探空数据可知，随着高度的增加，中国香港地区上空水汽密度整体逐渐降低，在10 km 左右，水汽密度含量已经趋近于0，而传统三维层析解算的结果在1.8 km 以上的高空解算的水汽密度质量较好，但是在低空时未能达到满意的效果。 同时，通过5 min 和10 min 的对比数据发现，时间的增长并没有明显改变数据质量。

表2 为10 min 滤波下探空数据与传统层析结果。

表2 10 min 滤波下探空数据与传统层析结果

通过表2 数据，可以更加详细了解在低空方面探空数据和传统层析方法的差异。

2.2 基于地势拟合的三维层析结果

图4 为基于地势拟合的三维层析方法在KHOH测站上空解算的水汽密度与探空资料的比对。

从图4 可以看出，2 次拟合曲面较3 次拟合曲面有更好的结果；通过5 min 和10 min 的对比数据发现，时间的增长并没有能够明显改变数据质量；通过2 次拟合曲面三维层析结果发现，在低空3 km 以下和6 km以上较传统三维层析方法具有更好的吻合程度，但是在3～6 km 区域表现较差。

表3 为10 min 滤波下探空数据与地势拟合层析结果。

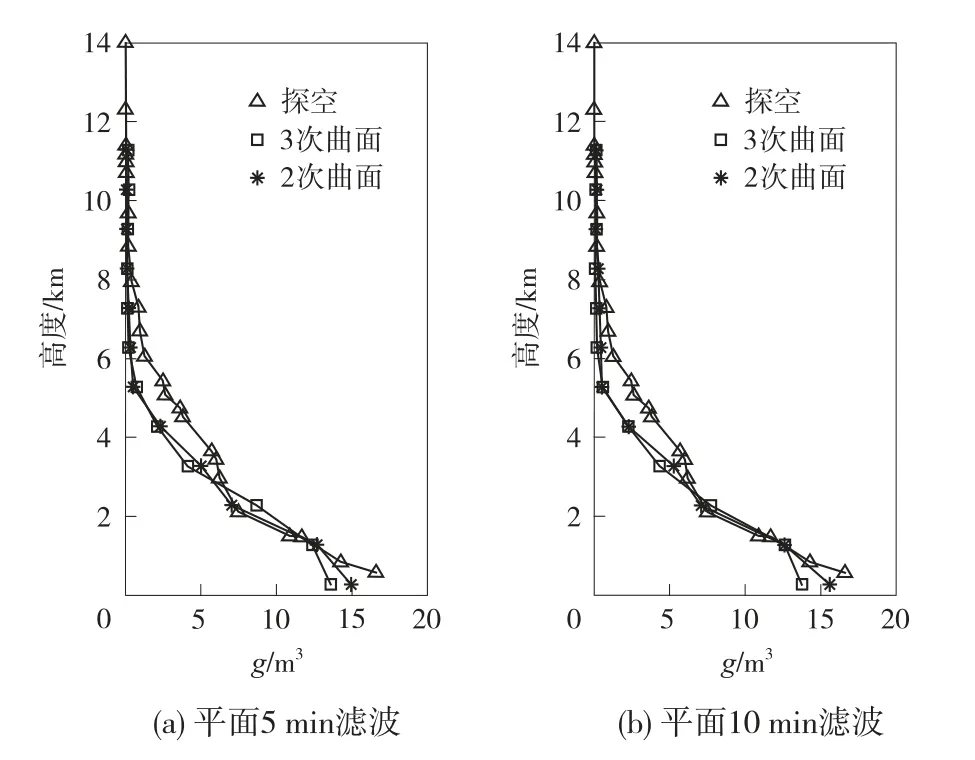
图4 基于地势拟合的三维层析方法

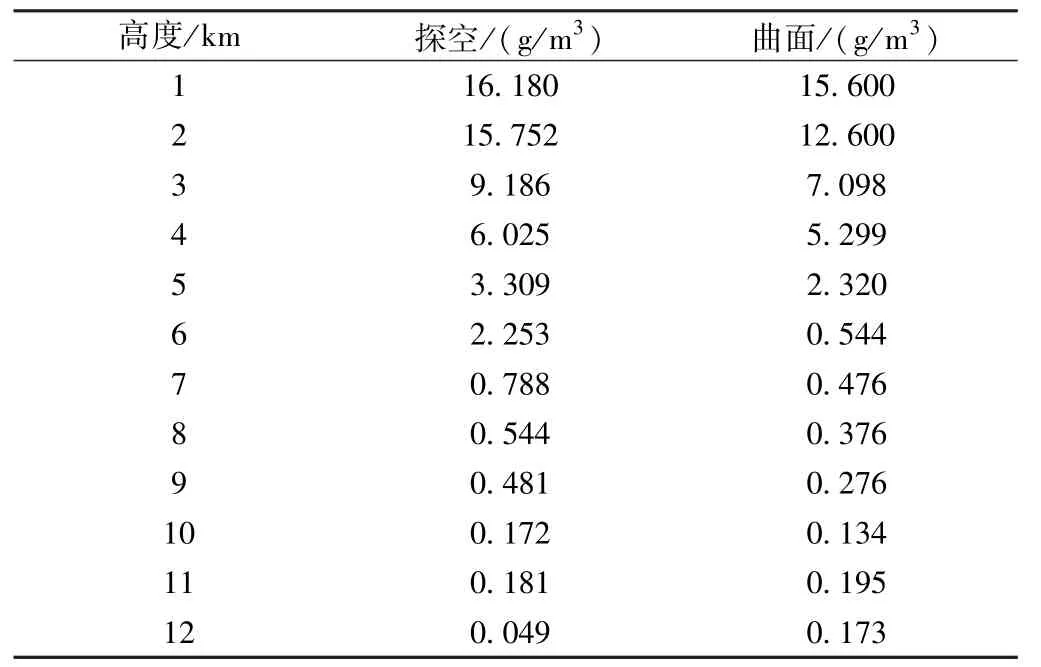
表3 10 min 滤波下探空数据与地势拟合层析结果

由表3 可知，基于地势拟合的三维层析方法在低空解算结果要明显优于传统层析方法解算的结果。 但是在3～6 km 区域解算的水汽密度结果质量较差。

2.3 基于地势拟合的三维层析方法与传统层析方法的组合应用

通过以上分析发现，传统层析方法在3 ～6 km 区间内有较好的精度，基于地势拟合的三维层析方法在低空3 km 以下和高空6 km 以上有较好的精度，时间的延长没有明显提高层析结果精度，2 次曲面较3 次曲面在低空三维层析结果上表现更好。 故将两种层析方法进行组合求解，使用传统层析方法解算3 ～6 km区间内的水汽密度，使用基于地势拟合的三维层析方法解算低空3 km 以下和高空6 km 以上的水汽密度。

图5 为两种层析方法组合求解情况。

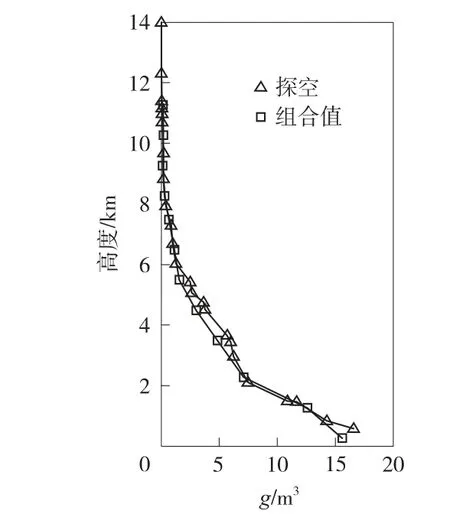
图5 组合三维层析方法

从图5 可以看出，组合后的三维层析方法较传统层析方法和基于地势拟合的三维层析方法均有了明显的精度提高，在与探空数据的比对上能够更好的吻合。

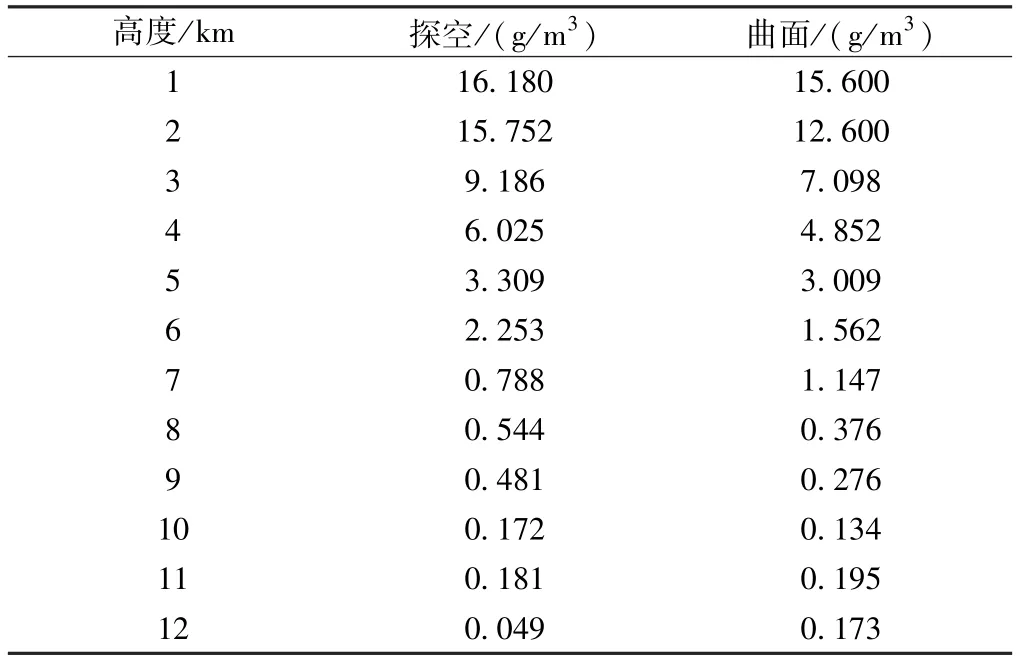
表4 10 min 滤波下探空数据与组合法结果

通过表4 数据可以明显看出，基于地势拟合的三维层析方法与传统层析方法的组合应用方法无论在低空和高空均表现良好，超过了单独的传统层析结算结果和单独的基于地势拟合的解算结果。 表5 给出3 个表格的均方差和相关系数结果。

表5 10 min 均方差和相关系数对照

从表5 中的数据可以看出，基于地势拟合的三维层析方法与传统层析方法组合应用方法在解算结果的均方差要明显低于基于地势拟合的解算结果和传统层析方法的解算结果，而且相关系数要高于后两种解算结果。

3 结论

提出基于地势拟合的三维层析方法，该方法能够有效解决测站之间的高差问题，并针对卫星信号与曲面穿刺点位置求解问题，提出根据拟合曲面将分层后的单个格网平面化进行求解。 结果表明，基于地势拟合的三维层析方法在低于3 km 及高于6 km 的区域较传统层析方法有较显著的精度提高，但是在中间区域精度较差。 最后提出基于地势拟合的三维层析方法与传统层析方法拟合的方案进行组合解算，证明该方法能够显著的提高三维层析精度。