基于FLAC3D的钢支撑架设滞后数值模拟研究

吴仲瑞，宋智勇，陆何，周贵贵

（1.中铁十六局集团北京轨道交通工程建设有限公司，北京 101100；2.合肥工大共达工程检测试验有限公司，安徽 合肥 230009；3.合肥工业大学土木与水利工程学院，安徽 合肥 230009）

0 前言

近些年来，为解决城市土地资源紧张和交通拥挤问题，城市地下空间得以大规模开发，而基坑工程作为地下空间开发必不可少的一环，其安全问题也越来越受到人们的重视。在实际施工过程中，钢支撑架设滞后这种不规范的操作将给基坑施工带来安全隐患。汤瑞[1]利用有限元软件MIDAS对基坑施工过程进行仿真模拟，以超挖厚度表征锚索安装不及时程度，研究了锚索滞后安装对围护结构内力、变形以及地表沉降的影响规律。胡之锋[2]采用有限元软件PLAXIS，建立有限元分析模型，以超挖厚度大小表征钢支撑滞后架设的程度，研究了不同位置钢支撑出现不同程度滞后架设对基坑围护结构内力变形及基坑周围地表沉降影响。代祥[3]以武汉地铁2号线机场线盘龙城车站出入口基坑为例，采用有限元软件PLAXIS 2D建立有限元模型，模拟分析基坑开挖过程有无架设钢支撑，对围护桩内力变化规律。

本文以合肥市轨道交通5号线黄河路车站基坑为例，采用有限差分软件FLAC3D对其进行三维建模，以超挖厚度的不同表征钢支撑架设滞后程度的不同，模拟计算基坑开挖过程中钢支撑架设滞后的不利工况，分析钢支撑架设滞后程度不同对基坑围护结构变形及地表沉降的影响大小。

1 工程概况

黄河路车站主体结构总长158m，标准段结构宽度21.9m，标准段基坑深度为23.11～23.50m，南侧端头井段基坑深度为24.87m，北侧端头井段基坑深度为25.44m。围护结构选用Φ1000@1300钻孔灌注桩排桩，标准段支撑体系为一道钢筋混凝土支撑和三道钢支撑，南北两侧端头井段为一道钢筋混凝土支撑和四道钢支撑。

根据黄河路站岩土工程勘察报告，车站土体参数如表1所示。

地下水主要有上层滞水以及基岩孔隙、裂隙水。浅部地下水主要赋存于素填土中，以上层滞水为主，水量微弱。勘探期间测得水位埋深为0.20～3.80m。基岩裂隙水主要赋存于岩石强、中风化带中，本车站基岩孔隙水埋藏较深，层顶埋深48.20～49.00m。地下水径流形式主要为孔隙间渗流。黏土和全风化岩富水性及透水性较差，连通性差，因此地下水径流一般。

2 基坑模型建立与工况设置

2.1 模型建立

以黄河路地铁车站基坑为工程背景，通过有限差分软件FLAC3D建立数值分析模型。根据基坑几何尺寸，拟定模型尺寸为280.2m×148.6m×73m(X×Y×Z)。模型共划分为514580个单元、546256个节点，模型网格划分如图1所示。

图1 模型网格示意图

土体本构采用莫尔-库伦模型，土体介质均假设为非线性、弹塑性介质材料[4-5]，模型中土体参数见表1。模型中排桩深度为37m，冠梁宽为1.5m，高1m。冠梁和排桩都采用实体单元，选取各向同性弹性模型，支撑体系采用beam结构单元[6]。模型材料参数如表2所示。

根据基坑整体变形受力特点，确定模型边界条件为：在模型的底面（Z=-36m)处施加竖向约束，在模型的四个侧面（X=-60.8m，X=219.4m，Y=-60.8m，Y=87.8m）处施加水平约束，模型的顶面（Z=37m）为自由面，不施加任何约束。

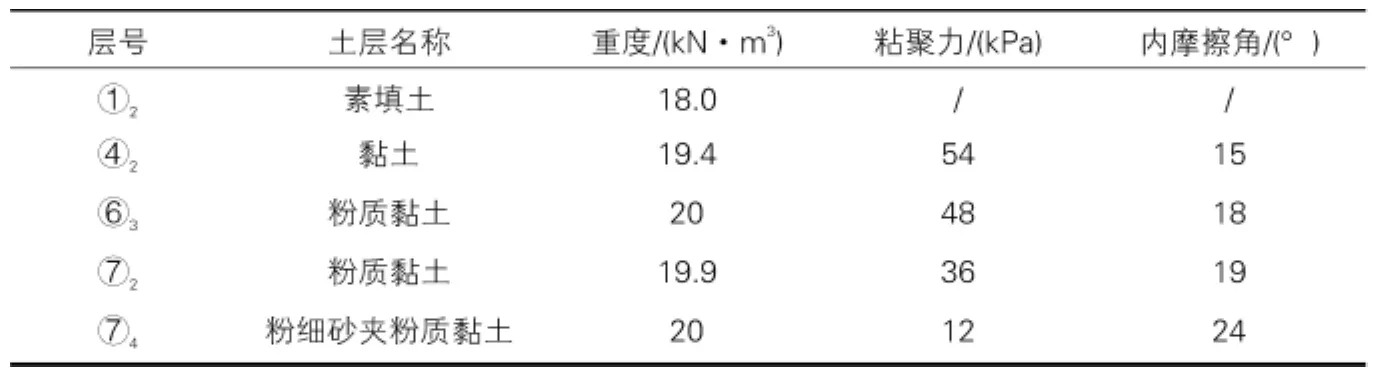
土体参数 表1

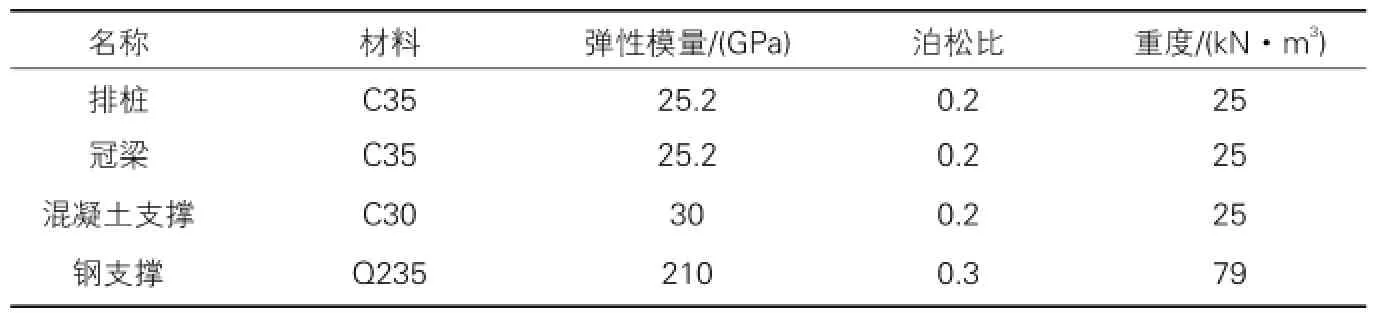
模型材料参数 表2

钢支撑滞后架设工况设置 表3

2.2 工况设置

第一道支撑为钢筋混凝土支撑，第二、三、四道支撑均为钢支撑，为便于研究各道钢支撑架设滞后的影响幅度，因此以土体超挖厚度大小表征钢支撑滞后架设程度(超挖厚度越大，钢支撑滞后架设程度越大)，工况设置如表3所示。

3 计算结果分析

利用FLAC3D分别模拟计算三道钢支撑在不同滞后程度 (超挖1m、2m、3m、4m)下，基坑围护结构变形和基坑外土体地表沉降的变化情况。

3.1 桩体侧向位移

由于工况1模拟的是正常按设计架撑，故将工况2、工况3、工况4的数值模拟结果与工况1进行对比分析，工况2、工况3、工况4的桩体侧向位移沿深度方向的分布如图2所示，图中超挖0m均是工况1计算得到的桩体侧向位移。

在工况1下，所有支撑均按设计架设，此时桩体最大侧向位移为23.4mm。在工况2下，第二道支撑架设滞后，当超挖厚度为1m时，桩体最大侧向位移为26.2mm，当超挖厚度达到4m时，桩体最大侧向位移增至35.4mm。桩体侧向位移随超挖厚度的增加而增大，在桩体深度方向中部增长得较多，在两端增长较小。

由图2可以看出，在工况3和工况4下，第三、四道支撑架设滞后时，桩体侧向位移变化规律与工况2类似，但随超挖厚度的改变，桩体最大侧向位移有所不同。在工况3下，第三道支撑架设滞后，当超挖厚度为1m时，桩体最大侧向位移为26.7mm，当超挖厚度达到4m时，桩体最大侧向位移增至36.4mm。在工况4下，第四道支撑架设滞后，当超挖厚度为1m时，桩体最大侧向位移为25.6mm，当超挖厚度达到4m时，桩体最大侧向位移增至34.7mm。

以超挖厚度为x轴，以桩体最大侧向位移为y轴，数据分布接近于直线，采用一次多项式y=ax+b来拟合超挖厚度与桩体最大侧向位移的关系，拟合的结果如图3所示。

由图3可以看出，在超挖厚度为0～4m的范围内，各工况下超挖厚度与桩体最大侧向位移均有着良好的线性关系。在工况2下，利用最小二乘法得到的超挖厚度与桩体最大侧向位移的线性回归线为y=2.97x+23.28，由此可得出，在第二道支撑滞后时，超挖厚度达到2.26m时，桩体最大侧向位移刚好达到控制值30mm。在工况3下，利用最小二乘法得到的超挖厚度与桩体最大侧向位移的线性回归线为y=3.22x+23.46，由此可得出，在第三道支撑滞后时，超挖厚度达到2.03m时，桩体最大侧向位移刚好达到控制值30mm。在工况4下，利用最小二乘法得到的超挖厚度与桩体最大侧向位移的线性回归线为y=2.82x+22.96，由此可得出，在第四道支撑滞后时，超挖厚度达到2.50m时，桩体最大侧向位移刚好达到控制值30mm。

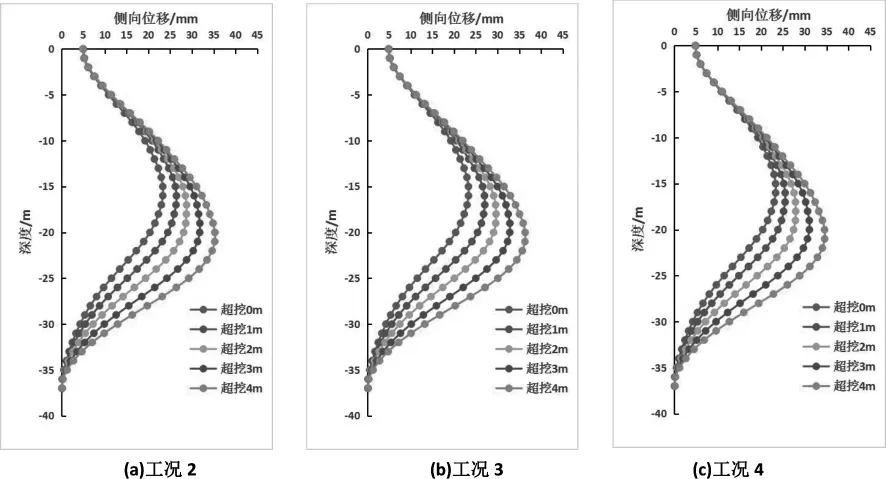
图2 桩体侧向位移

图3 超挖厚度与桩体最大侧向位移的关系

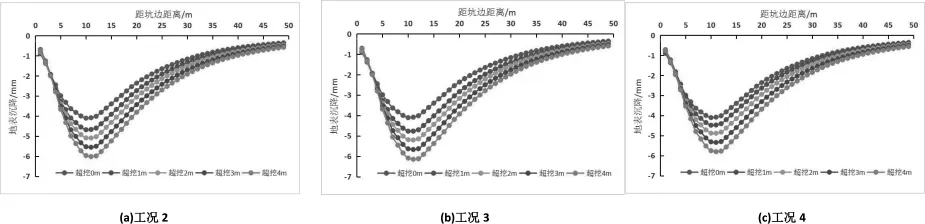
图4 地表沉降

图5 超挖厚度与地表沉降最大值的关系

3.2 地表沉降

将工况2、工况3、工况4的数值模拟结果与工况1进行对比分析，工况2、工况3、工况4的地表沉降的分布如图4所示，图中超挖0m均是工况1计算得到的地表沉降。

由图4可以看出，三种工况下基坑外土体地表沉降呈现一致的变化规律：地表沉降曲线都呈现为先增大后减小的“勺型”分布；各个工况下在距坑边5m以外的地表沉降量都是随超挖厚度的增加而增大的，而在距坑边5m以内的土体由于靠近围护结构，地表沉降量随超挖厚度的增加变化很小。

各工况随超挖厚度的改变，地表沉降最大值是不同的。与研究桩体最大侧向位移类似，以超挖厚度为x轴，以地表沉降最大值为y轴，采用一次多项式y=ax+b来拟合超挖厚度与地表沉降最大值的关系，拟合的结果如图5所示。

由图5可以看出，在超挖厚度为0～4m的范围内，三种工况下超挖厚度与地表沉降最大值均有着良好的线性关系。在工况2下，利用最小二乘法得到的超挖厚度与地表沉降最大值的线性回归线为y=0.444x+4.144。在工况3下，利用最小二乘法得到的超挖厚度与地表沉降最大值的线性回归线为y=0.469x+4.168。在工况4下，利用最小二乘法得到的超挖厚度与地表沉降最大值的线性回归线为y=0.401x+4.072。在三种工况下，地表沉降最大值都远远小于控制值30mm。

4 总结

以黄河路地铁车站基坑工程为研究对象，基于FLAC3D软件，以超挖厚度表征钢支撑架设滞后程度，分析钢支撑滞后架设对围护结构侧向变形和地表沉降的影响程度，得出以下结论：

①三种工况下桩体侧向位移随超挖厚度的增加而增大，在沿桩体深度方向中部增长得较多，在两端增长较小；

②在超挖厚度为0～4m的范围内，三种工况下超挖厚度与桩体最大侧向位移均有着良好的线性关系；桩体最大侧向位移达到控制值30mm时，第二、三、四道支撑超挖厚度分别不得超过2.26m、2.03m、2.50m；

③三种工况下基坑外土体地表沉降均呈现为先增大后减小的“勺型”分布，在距坑边5m以外的地表沉降量都是随超挖厚度的增加而增大的，而在距坑边5m以内的土体由于靠近围护结构，地表沉降量随超挖厚度的增加变化很小；

④在超挖厚度为0～4m的范围内，三种工况下超挖厚度与地表沉降最大值均有着良好的线性关系，在三种工况下，地表沉降最大值都远小于控制值30mm。