考虑资金时间价值的给水管网经济流速计算与影响因素研究
吴雨航,胡晓兰,喻霈雯,薛英文,3
(1.武汉大学土木建筑工程学院,武汉 430072;2.湖南大学设计研究院有限公司,长沙 410006;3.湖北省城设综合防灾与消防救援工程技术研究中心,武汉 430072)
0 引 言
我国的经济流速计算方法是在苏联的“经济因素法”的基础上推广应用得到的,综合考虑管网建设投资费用、运行动力费用、大修费用,使三者之和最小的流速即为经济流速[1]。经济流速是一个动态的概念,它与各种技术经济条件有关,这些影响因素都会随着时间、地域的不同而改变。
几十年来,国内的给水管网设计中,多采用平均经济流速确定管径,沿用的计算数据和计算方法都是十几年前甚至几十年前的,在当时可能是经济合理的,但在目前看来,这些指标已经不能满足经济性的要求。
以武汉地区为例,2019年与2007年的市政工程人工单价相比,涨幅超过200%[2, 3]。由于经济流速是一个以经济性作为主要目标的参数,价格的变化必然会影响经济流速的大小。因此,重新计算当前价格下的经济流速是非常必要的。同时,经济流速的合理确定,对于降低工程建设投资费用、降低后期运营维护费用等都具有十分重要的意义。
本文在充分考虑资金时间价值的基础上,按照年费用折算值最小法原则建立给水管网优化设计数学模型,分析影响经济流速的多种因素,以期得到最新经济条件下给水管道的经济流速。并通过实际工程案例来分析新经济流速对管网投资的影响。
1 给水管网经济流速的计算
(1)给水管网优化设计目标函数。给水管网的总费用包含管网从建设到报废期间的全部费用,主要指管网建设费用、大修费用以及运行费用之和,在管网优化计算中通常用管网年费用折算值表示[1],它可以看作是管网建设投资费用的年平均值和管网运行费用的年平均值二者之和。
给水管网年折算费用W计算公式如下[1,4]:
W=
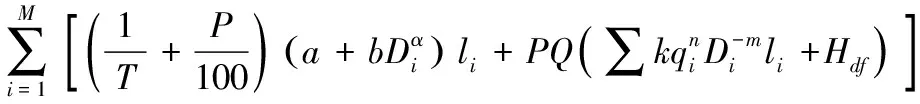
(1)
式中:T为管网建设投资偿还期(年)取15~20 a;li为编号为i的管道长度,m;D为管道直径,m;a,b,α为管道单位长度造价公式的相关统计参数;p为管网年大修费率,%;P为管网动力费用系数,(元·m-3·s-1·m-1·a-1);Hdf为节点服务水头与节点和泵站之间地面高差之和,m;Q为泵站最大时供水流量,m3/s;qi为管段流量,m3/s;M为管道总数,i从1~M;k,n,m为水头损失常数和指数。
(2)目标函数修订。传统给水管网优化目标函数在计算年费用平均值时,忽略了一个很重要的概念----资金的时间价值。采用管网年折算费用作为目标函数,即将综合费用折算成为每年等额支付的金额,以年折算费用最小为优化目标。
根据等额支付现值和终值[5]得到:
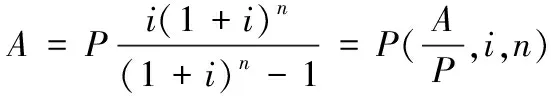
(2)
式中:i为每个计息周期的利率;n为计息周期数;P为现值;A为连续出现在各计息期末的等额金额。
因此,可将传统的年折算费用目标函数修订为:
(3)
经过修订的目标函数,考虑了工程投资偿还期内资金的时间价值,将投资费用转化为每年等额支付金额加以计算,更具经济性和合理性。
(3)平均经济流速计算公式。在给水管网的设计中,通常可以采用平均经济流速法和界限流速法来确定经济流速,并以此为依据确定经济管径[6-8]。令修订后的目标函数W′对管径Dj求一阶偏导数,并令其等于0。
整理得到经济管径的计算公式:
(4)
经济因素参数f′:
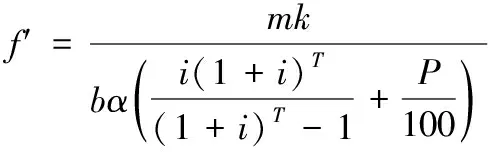
(5)
得到经济流速计算公式:
(6)
与传统的年折算费用函数相比,修订后的目标函数w′从经济动态分析的角度考虑了资金的时间价值,其经济流速计算结果更优,更具有推广的意义。
2 给水管网经济流速影响因素
2.1 管道造价
管道的总造价对经济流速计算结果会产生较大影响。通过表1中的数据可以发现,武汉地区近十年来各类给水管道管材的价格平均涨幅超过30%。
通过经济流速计算公式(6)可以发现,管道造价对经济流速的影响主要通过参数b、α在计算中的表现[9]。根据实际的造价拟合出准确的参数,对经济流速计算结果的合理性具有重要影响。
以武汉市承插球墨铸铁管为例,对其不同年份之间的单位长度造价进行对比(见图1),近十年来管道单位长度造价呈现大幅上涨的趋势,平均涨幅约35.52%。
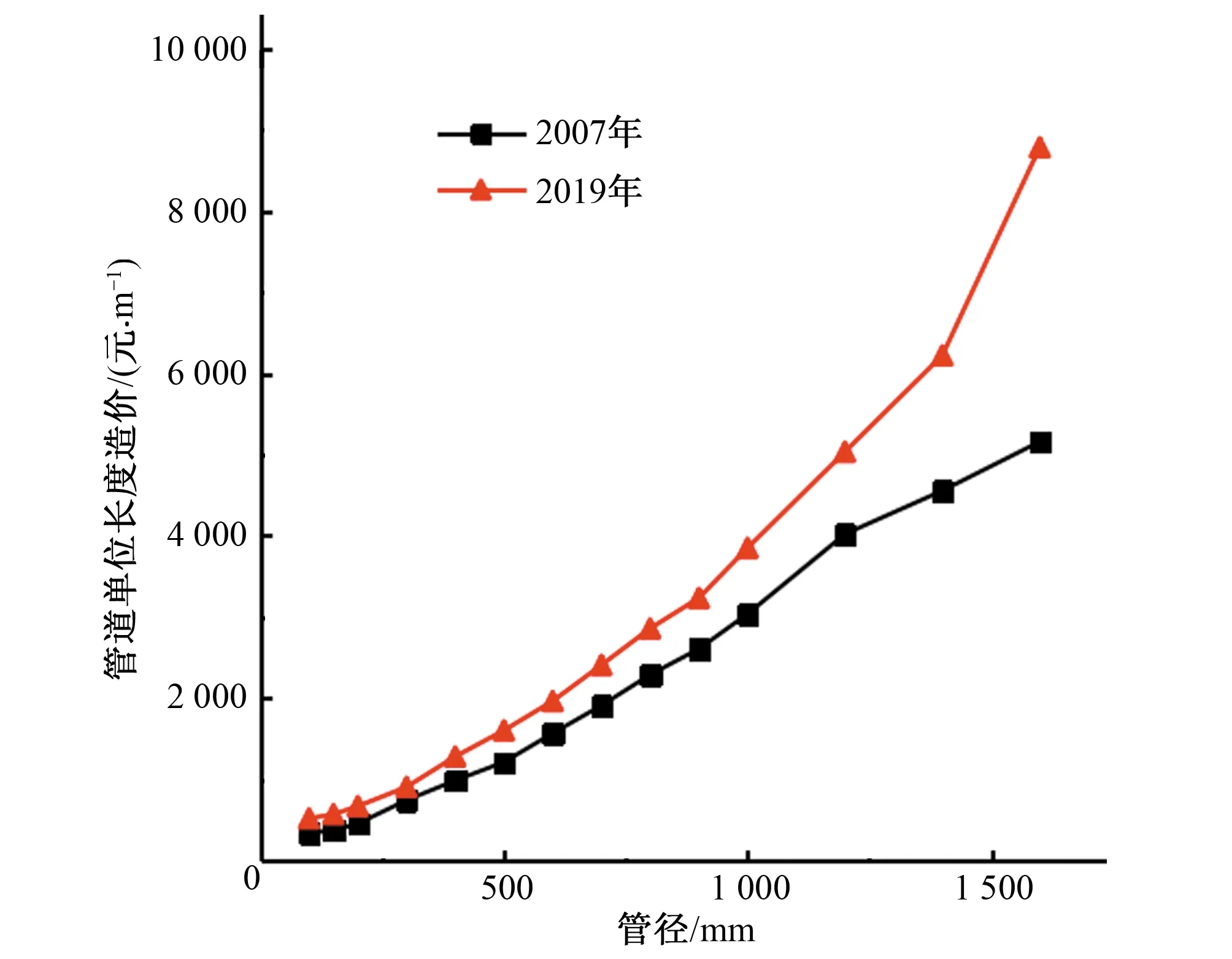
图1 承插球墨铸铁管单位长度造价对比图(武汉)
本研究中在保持其他参数相同的条件下(泵站电费变化系数0.55,泵站最大时综合效率0.7,电价E=0.6 元/kWh,管网大修费率2.5%,年利率2%,管网建设投资偿还期20 a),采用修订过的计算公式(6),计算不同年份下的经济流速,分析价格变化对经济流速的影响。
从表2和图2中可以看出,设计流量较小(10~300 L/s)时,2019年经济流速与2007年相比不增反减,且随设计流量逐渐增大,变动幅度越来越小。对照表3可发现,这种变化趋势的原因是:虽然规格较小的管道的造价增长幅度较大,但可采用较低的经济流速的方式使得管网的运行动力费用降低,以实现降低管网年折算费用的目的。在设计流量较大(300~2 000 L/s)时,2019年的经济流速较2007年有所增长,因在设计流量大、管径规格较大的情况下,随管道造价的大幅增长,管网的建设投资费用和大修费用成为影响管网年折算费用的最主要因素,通过提高经济流速来控制经济管径的规格使得年折算费用降低。

表2 承插球墨铸铁管经济流速对比(武汉)

表3 承插球墨铸铁管经济管径对比(武汉)
2.2 泵站电费变化系数
泵站电费变化系数指的是泵站的全年输水平均时电费(能耗)与最大时电费(能耗)之比,体现了给水管网输水耗能的不均匀性。我国大部分水厂二级泵站都采用了变频泵,正常运行的情况下水泵能保持较高的效率,泵站的综合效率可认为基本保持不变。
泵站电费变化系数γ的计算公式如下[1]:
(7)
以2019年武汉市球墨铸铁管为例,在保持其他参数不变的条件下,观察泵站电费变化系数γ的变化对经济流速计算结果的影响。
从图3和表4可以看出,经济流速计算结果与泵站电费变化系数呈现出负相关的变化关系。γ越小说明在保持最大时流量、最大时能耗的条件下,实际能耗越小,即年运行动力费用越小,其在管网总费用中所占比重较轻,则管网的建设费用对管网总费用有较大的影响。因此经济流速适当增大,有助于减小管径、降低管网建设费用,从而使得管网总费用最优。γ越大则说明管网的运行动力费用对管网总费用的影响也随之增大,此时经济流速适当减小,通过节省运行动力费用以实现总费用最优。实际应用中γ的不均匀性是水量、水压、电价共同影响下的结果,计算时需要全面考虑。
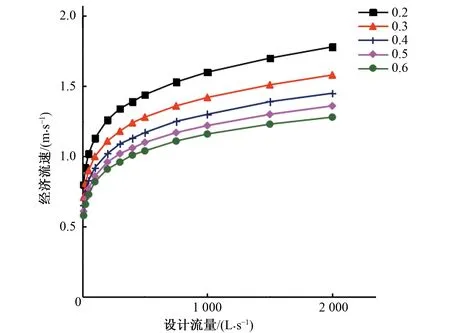
图3 承插球墨铸铁管在不同泵站电费变化系数下的经济流速
2.3 电 价
在给水管网的总费用中,电价对管网的运行动力费用有着直接影响,电价越高,管网运行费用越高。以武汉市承插球墨铸铁管为例,分别计算2007年和2019年在不同电价下的经济流速,计算结果见图4和表5。
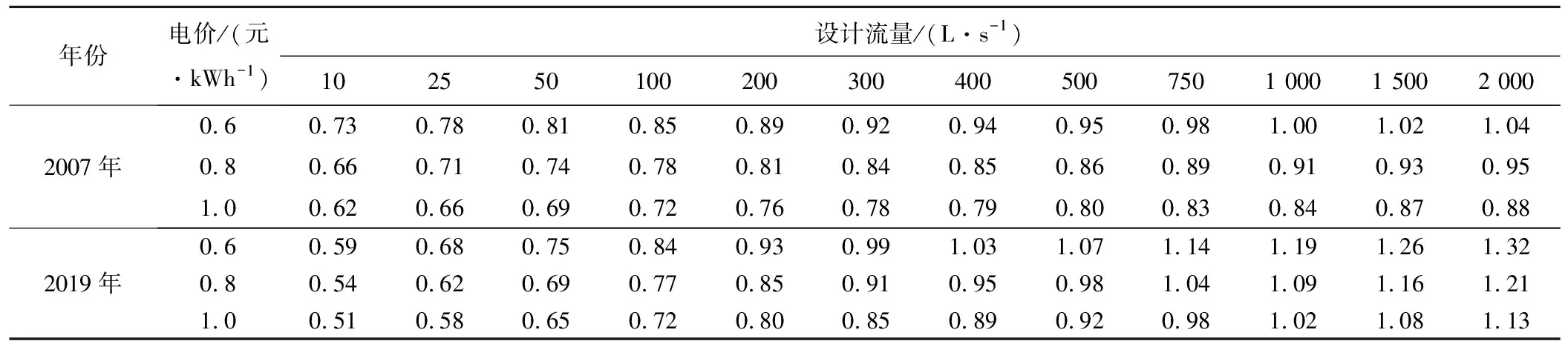
表5 不同电价下承插球墨铸铁管经济流速 m/s
从图4看出,在其他参数保持一致的情况下,经济流速与电价呈现负相关的关系。同一种管材的经济流速会随着电价的升高而减小,是因为当电价升高时会导致给水管网的运行动力费用也随之提高,降低设计流速可以减小在输水过程中的水头损失,以降低管网的运行动力费用。因此,在电价提高的情况下,可以通过适当地降低经济流速值,降低管网的运行动力费用;而在电价降低的情况下,也可以通过适当地提高经济流速值,以减小管道管径、降低管网的建设投资费用和大修费用的部分,实现管网年折算费用的平衡最优。
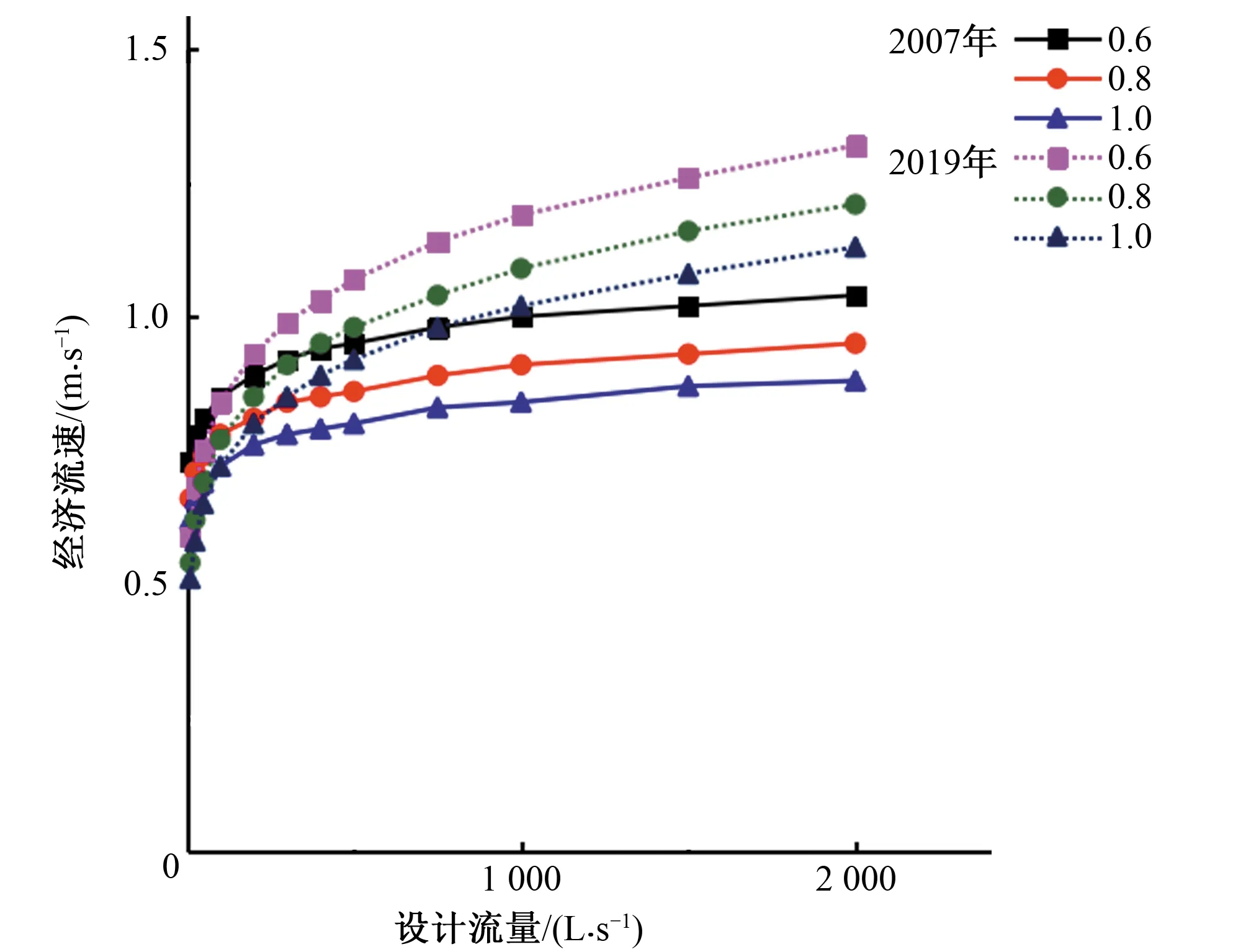
图4 不同年份、不同电价下承插球墨铸铁管的经济流速
3 实例计算与应用
3.1 实例计算
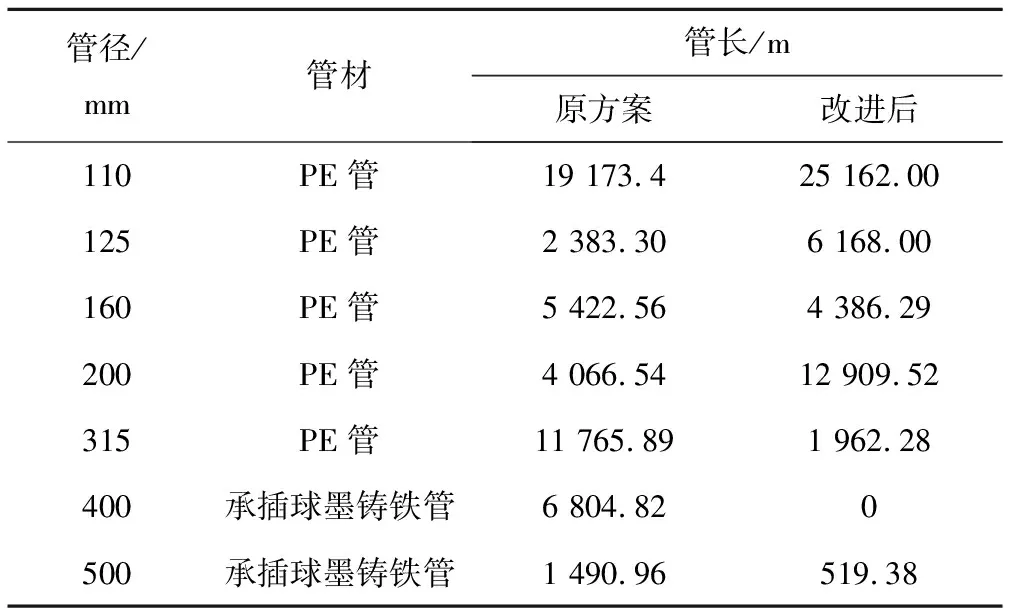
本文以某镇镇区给水管网为实例进行计算。镇区最高日设计供水量Qd=1.50 万m3/d。地面标高为59~61 m,用地高差在2 m左右,地势平坦,控制点水压要求为24 m。原方案经济流速选择范围为100 mm 管网布置如图5所示。管网按远期规模设计,按最高日最高时用水量计算,Q=343.88 L/s。原管网设计方案与新经济流速下管网设计方案对比见表6。 图5 XX镇镇区给水管网计算图 表6 承插球墨铸铁管和PE塑料管的新经济流速 L/s 本工程时变化系数Kh=2.0,日变化系数Kd=1.5,Kz=Kh·Kd=3.0。泵站电费变化系数0.31,水泵效率η取85%。泵站最大时电价E取1.05 元/kWh。年利率i按银行贷款利率取4.9%,投资偿还期取20 a。经综合比较后,管径在300 mm以上管道采用承插球墨铸铁管、300 mm及以下配水干支管道采用PE塑料管。利用新经济流速计算承插球墨铸铁管、PE塑料管在新的价格水平下的经济流速,计算结果见表6。 经过统计,工程中管材用量见表7。与原方案相比,在采用了新经济流速的设计方案中,400 mm及以上规格的承插球墨铸铁管用量大幅减少,110、200 mm规格的PE管用量显著增多。 表7 管材用量表 采用最新市场价格下计算得到的管道指标基价,计算原方案和采用新经济流速改进后的两种方案的管网总费用,结果见表8。 表8 两种设计方案管网年折算费用统计 万元 改进后方案的管网建设投资费用年折算值和年大修费用比原方案节省了约44.12%,管网总费用节省约21.92%。因此通过应用新的经济流速可以实现管道规格的控制和管网建设费用的降低。采用了新经济流速计算的设计方案较采用现行常用经济流速的设计方案,在经济性上更加真实可靠。 本研究在给水管网优化的思想基础上,以经济流速作为研究对象,并从目标函数的建立、计算方法、目标函数的优化三个方面介绍了给水管网经济流速的计算。本文还讨论了管道造价、泵站电费变化系数、电价几个主要因素对于经济流速的影响如下。 (1)随着管道造价的提高,在设计流量较小时,使经济流速降低,以此来减小管网的运行动力费用,实现年折算费用最低;在设计流量较大时,使经济流速增大,以此来控制管网建设费用,通过建设费用和运行费用的平衡来实现总费用最低。 (2)经济流速计算结果与泵站电费变化系数和电价大小呈现出负相关的变化关系。 (3)通过实例工程验证,使用新的经济流速,可以大幅节省管网建设费用和管网运行费用,体现了新经济流速的优越性,同时也证明了经济流速重新计算的必要性。 □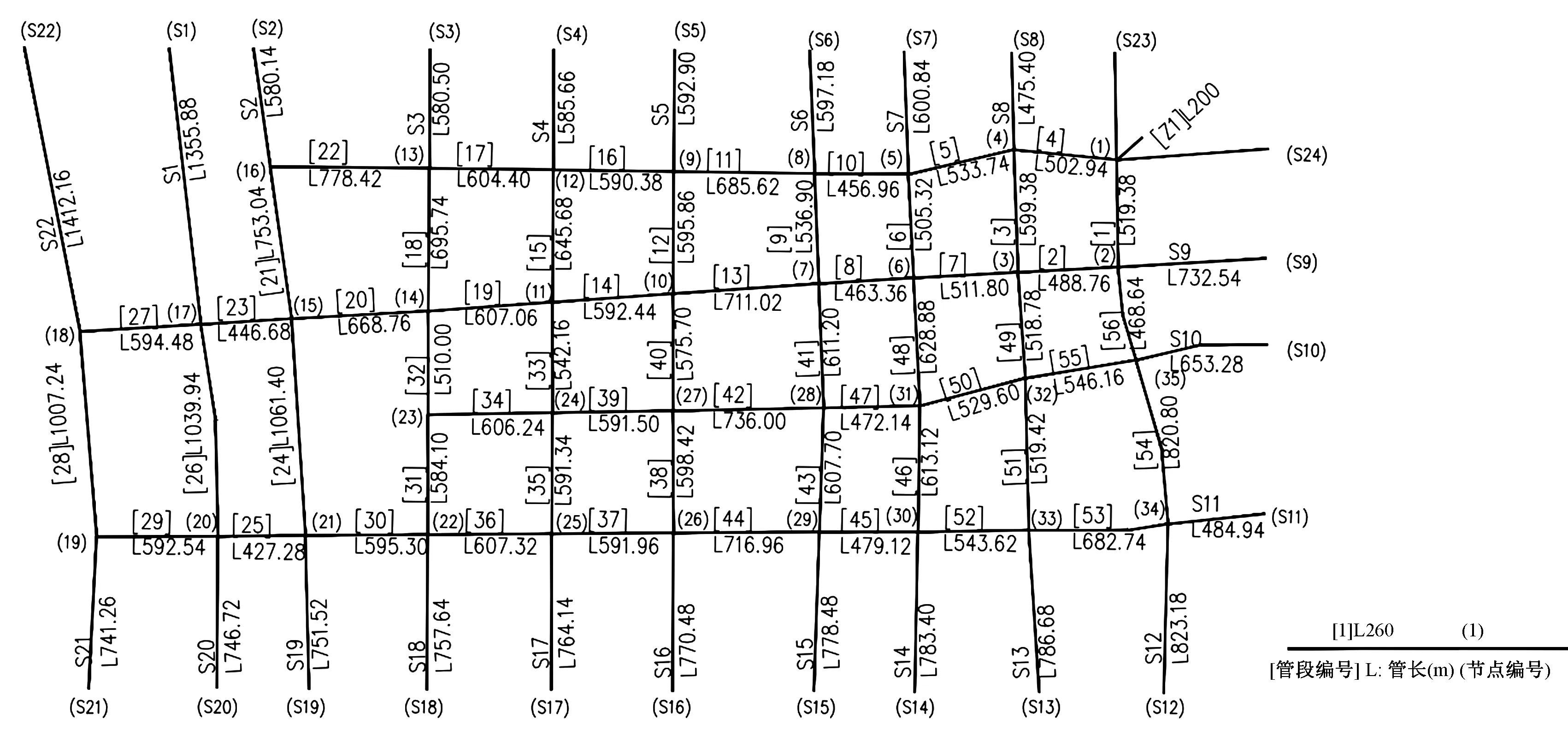

3.2 方案对比

4 结 论

