基于线性矩阵不等式的纯时滞系统稳定性分析与控制器设计
翁发禄, 耿飞跃, 丁元春
(1.江西理工大学电气工程与自动化学院, 赣州 341000; 2.江西理工大学资源与环境工程学院, 赣州 341000)
纯时滞系统普遍存在于化工过程、金属冶炼等场所[1-5]。例如,冶金加热炉的传热、蒸汽锅炉的加热、化学反应过程等均可描述成纯时滞系统的形式。此外在燃煤锅炉中对风煤水的控制也存在纯时滞现象。由于纯时滞的作用,系统状态无法第一时间响应控制信号的改变,而是经过一段时间后产生响应。在系统控制器设计中,如果未恰当考虑时滞对系统的影响,有可能造成控制性能下降,甚至闭环系统不稳定。在过去的几十年内,已有学者对纯时滞系统做了大量的研究。例如,夏百花等[6]对一阶纯时滞系统的PID(比例、积分、微分)控制和Smith预估补偿控制进行了分析与设计。刘尚标[7]设计了一种倒数模型用于纯时滞系统的控制。杜星瀚等[8]利用干扰观测器对Smith补偿控制的结构进行了改进。Khusainov等[9]考虑了线性纯时滞系统的相对可控性及镇定问题,获得了柯西问题的积分形式解。He等[10]研究了一种纯时滞脉冲竞争系统的衰减和稳定性,并获得了改进的稳定性条件。Liang等[11]介绍了多项式的分数延迟矩阵余弦和正弦,给出了纯时滞分数线性系统柯西问题解的表示形式。虽然纯时滞系统提出较早,但是大部分已有成果是在经典控制理论的基础上进行讨论,基于状态空间的相关成果较少。由于状态空间能够清晰描述系统内部结构,方便处理多输入多输出系统,因此,进一步获得基于状态空间描述的纯时滞系统相关成果是必要的。
线性矩阵不等式(LMI)解决系统控制问题最早可追溯到一百多年以前[12]。随着计算机技术的发展及内点法求解的提出,LMI受到广大科研人员的关注,同时,采用LMI解决系统控制问题也已成为研究热点。例如,文献[13]基于LMI讨论了2D奇异系统的稳定性分析与综合问题。文献[14]基于LMI研究了结构系统的主动控制问题。毛凯等[15]在LMI中引入自由权矩阵实现了神经网络系统的全局稳定性分析。孙宜标等[16]基于LMI实现了直线伺服系统跟踪控制。基于增广LMI,Ge等[17]讨论了非线性柴油机系统的扩展保成本控制。基于LMI技术,魏新江等[18]针对随机多源干扰系统进行了复合容错控制器设计。但是,纯时滞系统的状态空间描述缺乏无时滞项,进而造成其基于LMI的相关理论成果极少。据所掌握文献可知,基于LMI的纯时滞系统控制问题研究仍旧不足。故此将主要基于LMI方法分析纯时滞系统的稳定性,并得到其稳定性分析与控制器综合的充分条件。考虑到参数不确定是实际系统必然遇到的问题[19-21],相关研究成果将进一步扩展至不确定参数系统。
1 模型描述
考虑如下纯时滞系统:
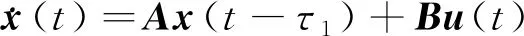
(1)
式(1)中:x(t)∈Rn、A∈Rn×n和B∈Rn×m分别为系统状态向量、系统状态矩阵及系统输入矩阵;τ1为系统纯时滞量;u(t)为系统控制输入。考虑到控制输入量的计算与传输需要消耗一定的时间,在此,假定控制输入信号的时滞量为τ2,可得状态反馈控制器:
u(t)=Kx(t-τ2)
(2)
式(2)中:K为状态反馈控制器增益。将控制器[式(2)]代入系统状态[式(1)]可得其闭环系统:
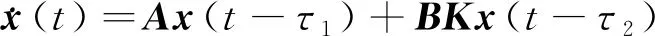
(3)
考虑到有:
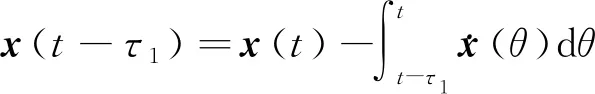
(4)
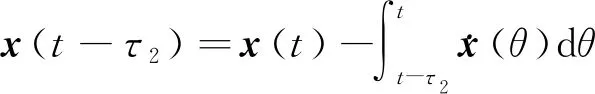
(5)
则闭环系统[式(3)]可进一步描述为
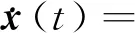
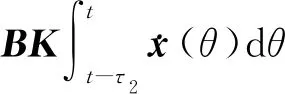
(6)
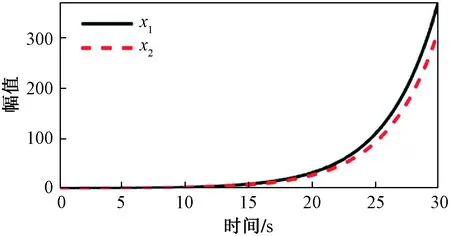
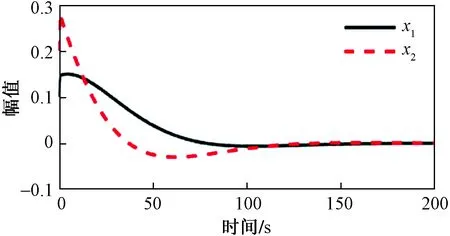
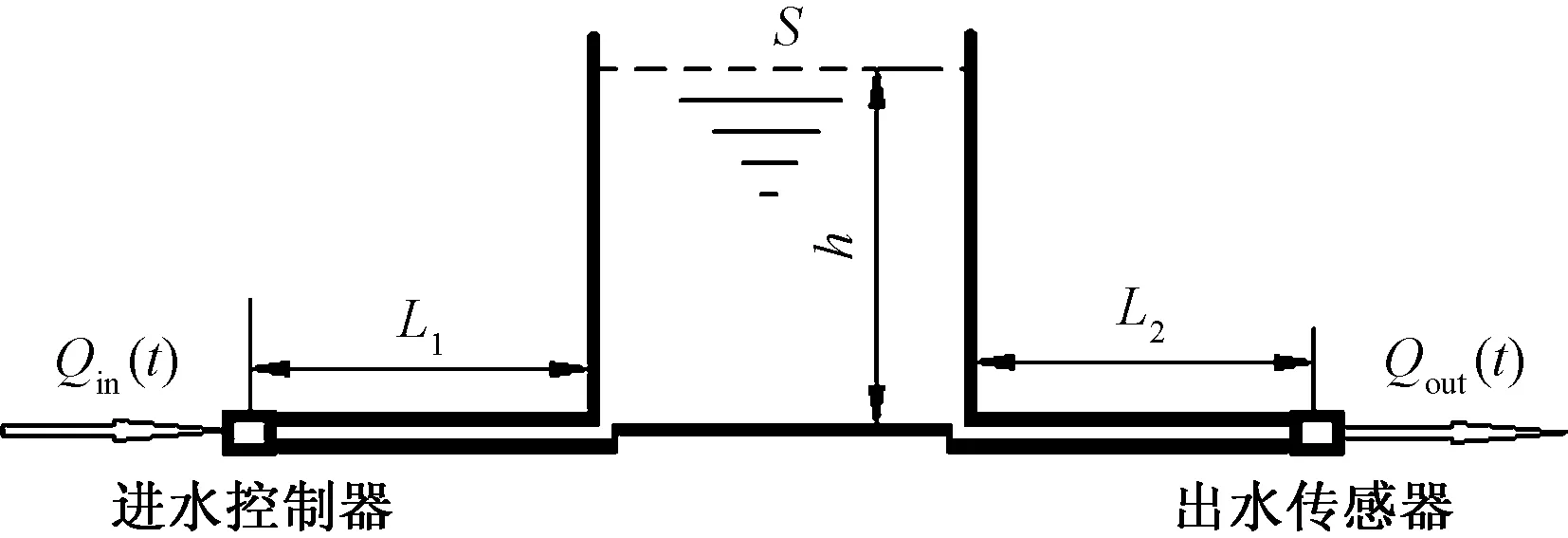
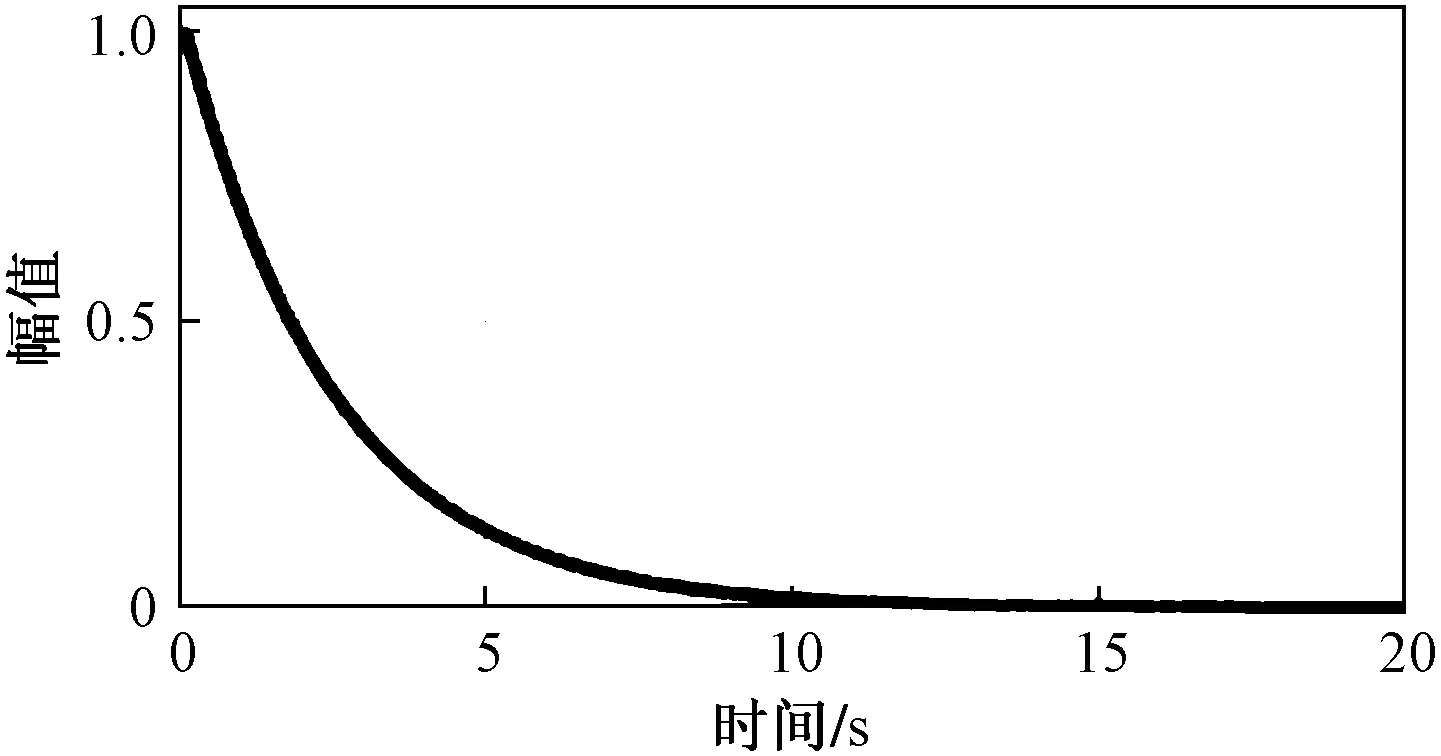
引理1[22]对于任意对称正定矩阵Π∈Rn×n,标量r1及r2满足r1 (7) 引理2[14]对于给定适当维数矩阵Ω=ΩT、Υ及Λ,有Ω+ΥF(t)Λ+ΛTFT(t)ΥT<0,其中FT(t)F(t)≤I,当且仅当存在任意σ>0,使得Ω+σΥΥT+σ-1ΛTΛ<0。 本节首先基于LMI推导出定理1用于纯时滞系统控制器设计,然后在定理1的基础上得到定理2用于纯时滞系统的稳定性分析。 (8) 式(8)中: 证明:选择正能量函数: V(t)=xT(t)Px(t)+ (9) 式(9)中: 对函数V(t)求导,可得: (10) 由引理1,有 (11) (12) 基于系统描述[式(6)],可知 (13) 式(13)中:S为适当维数的任意非奇异矩阵;β1、β2、β3为任意常数。综合式(10)~式(13),有 (14) 定理1给出了纯时滞系统[式(1)]镇定控制器存在的充分条件。在未找到线性矩阵不等式(8)可行解的情况下,可适当调整参数β1、β2及β3的值实现在更大范围内搜寻不等式(8)的可行解,也就是说β1、β2及β3增加了不等式(8)可行解的取值范围,降低了定理1的保守性。同时,如果令式(9)中的Q2=0,式(13)中的β3=0,K=0可以得到如下定理2用于判断纯时滞系统开环状态下的稳定性。 (15) 在参数β1、β2及β3给定的情况下,LMI[式(8)]及[式(15)]均为严格LMI,可以通过MATLAB的LMI工具箱直接求解,极大提高了定理应用的便利性。 考虑如下不确定纯时滞系统: (16) 式(16)中:x(t)、A、B及τ1的定义与系统(1)相同。ΔA、ΔB为不确定矩阵,且满足: [ΔAΔB]=MF(t)[N1N2] (17) 式(17)中:M、N1及N2为已知适当维数的常数矩阵;F(t)∈Rk×s是未知时变参数矩阵,且满足: FT(t)F(t)≤I (18) 基于定理1及定理2可得定理3及定理4保证系统[式(16)]的鲁棒稳定性。 (19) 式(19)中: 证明:将矩阵A替换成A+ΔA,不等式(8)可描述为 (20) 由引理2可知,不等式(20)成立,当且仅当存在σ>0,使得不等式(21)成立。 (21) 基于舒尔补引理可知,不等式(21)成立等价于不等式(19)成立。 定理4对于任意给定时滞τ1,存在适当维数的对称正定矩阵非奇异矩阵及任意常数β1、β2及σ>0使得线性矩阵不等式(22)成立,则纯时滞系统[式(16)]开环状态下是鲁棒稳定的。 (22) 定理4的证明与定理3的证明类似,在此省略。 例1考虑如下纯时滞系统的稳定性: (23) 令β1=β2=1,求解定理2可知线性矩阵不等式(15)有解,且有 也就是说,该系统[式(23)]稳定。现令初始条件满足x(t)=[0.1 0.2]T,t∈[-1, 0],经计算机仿真可得系统的状态响应曲线,如图1所示,从图1可知该系统状态收敛,即定理2是有效的。 图1 纯时滞系统[式(23)]开环状态响应曲线Fig.1 Open-loop state responses of the pure time-delay system (23) 例2考虑如下纯时滞系统: (24) 经求解定理2可知线性矩阵不等式(15)无可行解,即该系统开环不稳定(开环状态响应如图2所示,初始条件同例题1)。现令β1=β2=β3=1,求解定理1可知线性矩阵不等式(8)有解,且有 进而可得纯时滞系统[式(24)]镇定控制器为 (25) 经计算机仿真可得闭环系统的状态响应曲线(如图3所示,初始条件同例题1),从图3可知纯时滞系统[式(24)]在控制器[式(25)]的作用下稳定,即定理1用于纯时滞系统控制器的求解是有效的。 图2 纯时滞系统[式(24)]开环状态响应曲线Fig.2 Open-loop state responses curves of the pure time-delay system (24) 图3 控制器K1作用下,纯时滞系统[式(24)]闭环状态响应曲线Fig.3 State responses curves of the nominal pure time-delay system (24) controlled by K1 例3考虑纯时滞系统[式(24)]存在如下不确定性M=[0.1 0]T,N1=[0.2 0.1]T,N2=[0.2],F(t)=sin(2t)。令β1=β2=β3=1,求解定理3可知线性矩阵不等式(18)有解,且有 进而可得纯时滞系统[式(24)]存在参数不确定情况下的镇定控制器 (26) 经计算机仿真可得闭环系统的状态响应曲线(如图4所示,初始条件同例题1),从图4可知不确定纯时滞系统在控制器[式(26)]的作用下稳定,即定理3用于不确定纯时滞系统鲁棒控制器的求解是有效的。 图4 控制器K2作用下,参数不确定纯时滞系统[式(24)]的状态响应Fig.4 State responses curves of the uncertain pure time-delay system [formula(24)] controlled by K2 例4考虑图5所示水箱水位控制。h及S分别为水位的高度及水箱的横截面积;进水控制器及出水流量传感器安装在进出水管的两端[Qin(t)及Qout(t)分别为进出水流量];进出水管的长度分别为L1及L2,L1及L2分别对进出水造成τ2及τ1的时滞量。出水口处于自由出水状态,有Qout(t)=εh(t-τ1),其中ε为常数。系统被控参数为水箱水位h,控制输入为进水流量Qin(t)=K3h(t),K3为状态反馈控制器增益。基于以上分析可得系统描述为 (27) 图5 一阶水箱水位控制系统Fig.5 Single-tank water control system 图6 水箱系统状态响应曲线Fig.6 State responses curve of the single-tank water control system 在此,假定该系统有ε=0.1,S=1,τ1=0.1,τ2=0.15。现令β1=β2=β3=1,求解定理1可知线性矩阵不等式(8)有解,且有K3=[-0.286 5]。经计算机仿真可得闭环系统的状态响应曲线{如图6 所示,初始条件:h(t)=1,t∈[-0.12, 0]},从图6可知水箱系统在控制器K3的作用下稳定。 基于LMI实现了纯时滞系统的稳定性分析与控制器设计。首先,考虑到控制信号计算与传输需要消耗时间,在系统控制通道中引入了时滞。然后,基于矩阵变换将系统模型描述成含分布时滞的形式。其次,基于Lyapunov系统稳定理论及线性矩阵不等式技术,得到了系统稳定的充分条件。同时,相关成果扩展至系统参数不确定性情形。最后,通过实例分析验证了相关定理的有效性。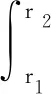
2 稳定性分析与控制器设计



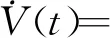
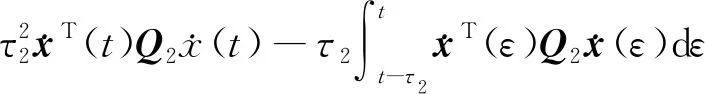
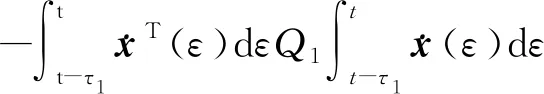
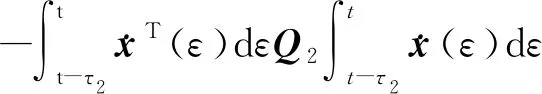
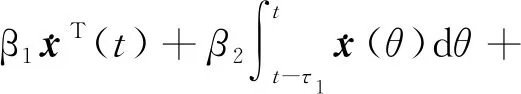
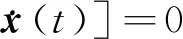

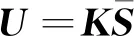

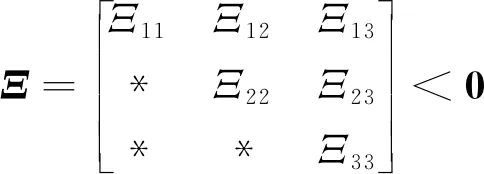
3 鲁棒性分析
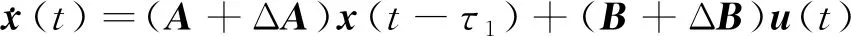


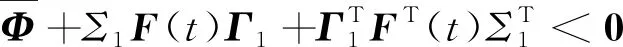
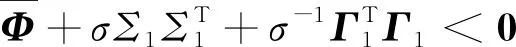
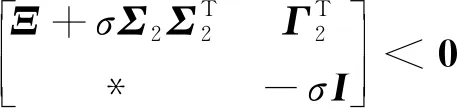
4 实例仿真
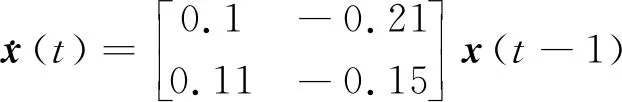
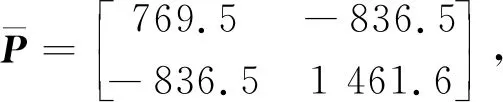


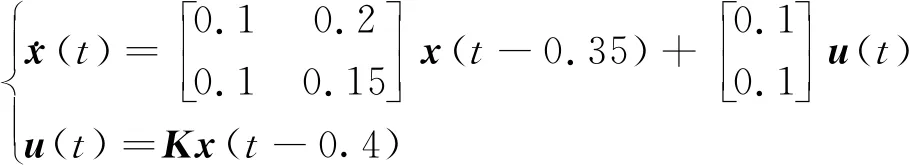
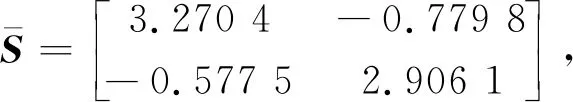
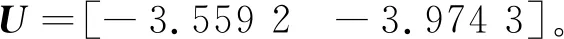
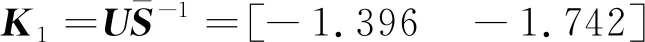

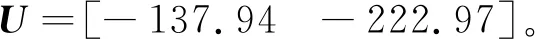
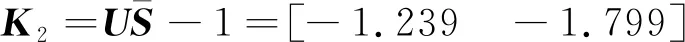

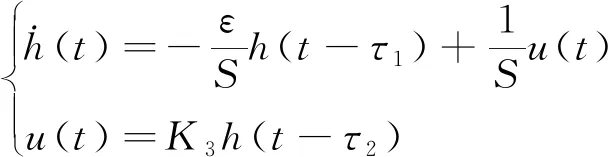
5 结论

