基于Abraham模型估算有机物表面张力

左丽华，陈六平

（1. 东华理工大学 化学生物与材料科学学院，江西 南昌 330013；2. 中山大学 化学学院，广东 广州 510275）

纯液体表面张力（σ）是物理和传递过程中重要的基础数据，在化工生产、工程设计等方面应用广泛。σ的测试方法很多，至今文献已公布的数据也较多，Jasper［1］曾系统整理了 1847—1969年间所公布的2 200多种物质在不同温度下的σ；Vargaftik［2］也提供了不少不同温度下σ的实验数据。随着精细化工的快速发展，现有温度范围内的σ数据已无法满足应用需求。而每年新递增的有机化合物种类繁多，逐一测定的实验量太大，因此发展纯液体尤其是纯有机物σ的计算方法有着重要的理论和实用意义。σ的估算方法很多，其中应用较为广泛、且计算精度在可接受范围内的估算纯物质σ的方法有基团贡献法［3-5］、人工神经网络法［6-7］、基于构效关系预测法［8-11］及其他估算方法［12-14］。这些估算方法大多仅限于结构简单的物质及有限的温度范围，且计算繁复、误差较大，有完善的空间。

本工作提出一种将σ这一宏观物性与微观分子间作用力相关联的一种新的计算方法。根据线性溶剂化能量关系（LSERs）理论和经验方程，提出了在不同温度下估算纯有机物σ的关联式。利用所得关联式对2 628个纯组分体系中的10个同系物进行了回归，得到了σ的关联方程，并对方程的相关性和外推适用性进行考察。

1 方程的推导

前期曾尝试从物质的本质出发，在分子间相互作用的水平上，结合LSERs理论［15］，采用Abraham分子结构参数，建立一个新的LSERs能量模型［16］，见式（1）；并结合温度的影响，对纯物质的蒸发焓和物质相互扩散系数进行估算，取得了良好的预测精度［17-18］。

式中，SP为系统性质；C为常数；e为过摩尔折射率系数；E为过摩尔折射率，cm3/mol；j为极化率系数；J为极化率，C·m2/V；a为氢键酸度系数；A为氢键酸度；b为氢键碱度系数；B为氢键碱度；v为特征分子体积系数；Vx为Abraham和Mc Gowan特征分子体积（反映分子大小），10-2cm3/mol。

在此基础上，利用上述Abraham特征线性溶剂化能量模型，对10类同系物的σ数据进行拟合，提出估算纯有机物σ的计算模型，拟为纯有机物σ的计算提供一种可供选择的方法。

由热力学原理及σ的定义可知，如果要将一个分子从液体内部移到表面，就需要克服液体内部周围分子对它的吸引力而做功。在恒温恒压可逆的条件下，形成新表面所消耗的功，将转化为表面层分子比内部分子多余的Gibbs自由能，即表面自由能。若体系组成不变，则可逆地使表面积增加（dAs）所需的功（W）为 δW=σdAs，又 -δW= d（G）Tp，得式（2）。

式中，σ为纯液体的表面张力，N/m；G为Gibbs自由能，J；T为温度，K；p为压力，Pa；As为液体的表面积，m2；n为物质的量，mol。

由此可见，σ是一个与能量相关的物理量，可应用LSERs原理。

已知热力学公式G=U+pV-TS，对于恒温恒压可逆过程，有式（3）存在。

式中，U为体系内能，J；V为体积，m3；S为熵，J/K。

又因为在考虑包括σ在内的广义压力情况下，Gibbs自由能可表示为式（4）。

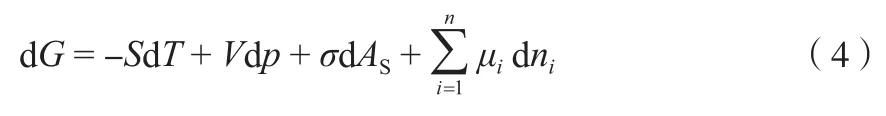
式中，μi为组分i的化学势，J/mol。

运用全微分性质，可得式（5）。

在恒温恒压、体积功为零的情况下，将式（5）代入式（3）可得式（6）。

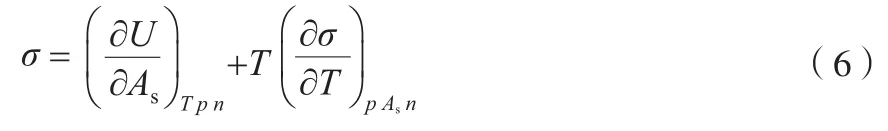
式（6）中右边第一项为增大单位表面积时内能的增量，即为液体内部分子相互作用力的表现。在纯液体中，分子之间的作用力包括氢键作用、偶极-偶极和偶极-诱导-偶极作用、色散力等。因此，根据LSERs理论，将增大单位表面积内能的增量（ΔU）表示为式（7）。

对于式（6）中右边第二项，经实验研究发现，在一定温度范围σ近似为温度的一次函数［19］，见式（8）。

因此，由式（6）～式（8）可建立估算纯液体σ的新方程：

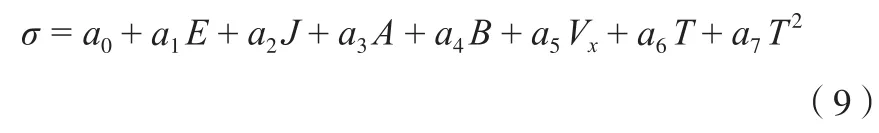
式中，ai为实验数据回归系数。

式（9）中a7T2项是针对某些物质具有接近临界状态的数据而增加的温度校正项。因为当温度趋向临界温度时，σ与温度之间的关系已不遵循线性关系，所以加入该项对温度进行较正，希望提高方程的计算准确度和精确度。

2 结果与讨论

2.1 数据的选取

本工作所选取的分子描述符主要来自Abraham等［16，20-22］发表的文献值。σ数据选自 Jasper等［1-2］整理的实验数据，以及文献［23-24］的实验数据。

2.2 方程相关性分析

选取212种液体有机物，包括烷烃、烯烃、炔烃、卤代烃、芳香烃、醇、醛、酮、酯和有机酸，共2 628个数据点，利用SPSS软件及Excel软件对实验数据及分子描述符进行回归，由最优化结果得到8个关联方程，方程式（9）中各类物质对应系数结果见表1。由表1可知，8个关联方程中各参数与σ的相关系数都达良好级以上，平均相对偏差均低于5%。

对上述各类方程σ数据分别做正态分布，结果见图1。由图1可知，8类有机化合物在临界温度以下范围内的σ估算值的残差都接近正态分布。

表1 计算σ的方程式（9）中各项系数Table 1 Coefficients in the equation (9) for calculating surface tension(σ)

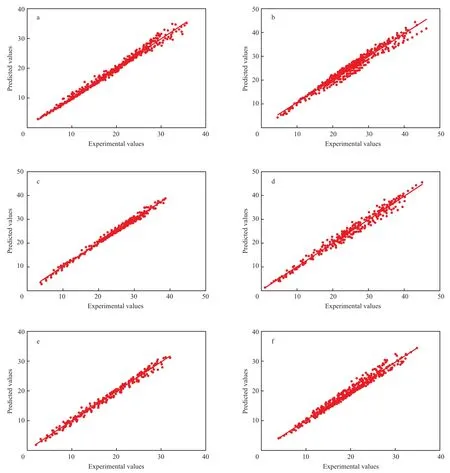
图1 8类有机化合物σ残差的正态分布Fig.1 Normal distribution for σ residuals of 8 kinds of organic compounds.

2.3 方程外推适用性分析

将方程与应用较普遍的Macleod-Sugden关联式和Brock-Bird关联式［3］的计算值相比较，结果见表2。由表2可知，本方程对各类有机物液体σ的预测值与实验值相比，大多数情况下预测偏差都在5%以下，且温度范围较广，有的甚至接近临界温度。本方程估算值偏差在大多数情况下比Macleod-Sugden和Brock-Bird方程的预测偏差小，特别是在高温时。Macleod-Sugden方程和Brock-Bird方程应用于某些种类化合物时会产生较大误差，也就是说这两个方程的普适性受到限制，如Brock-Bird关联式不适用于具有强氢键（极性）的化合物（酸、醇等）。

为了进一步验证方程的外推适用性，另取了8类未参与回归的化合物在298 K时的σ实验数据，与所得方程计算值相比较，结果见表3。由表3可知，用本工作模型对化合物的σ进行估算时，大部分物质的预测偏差都在5%以下。

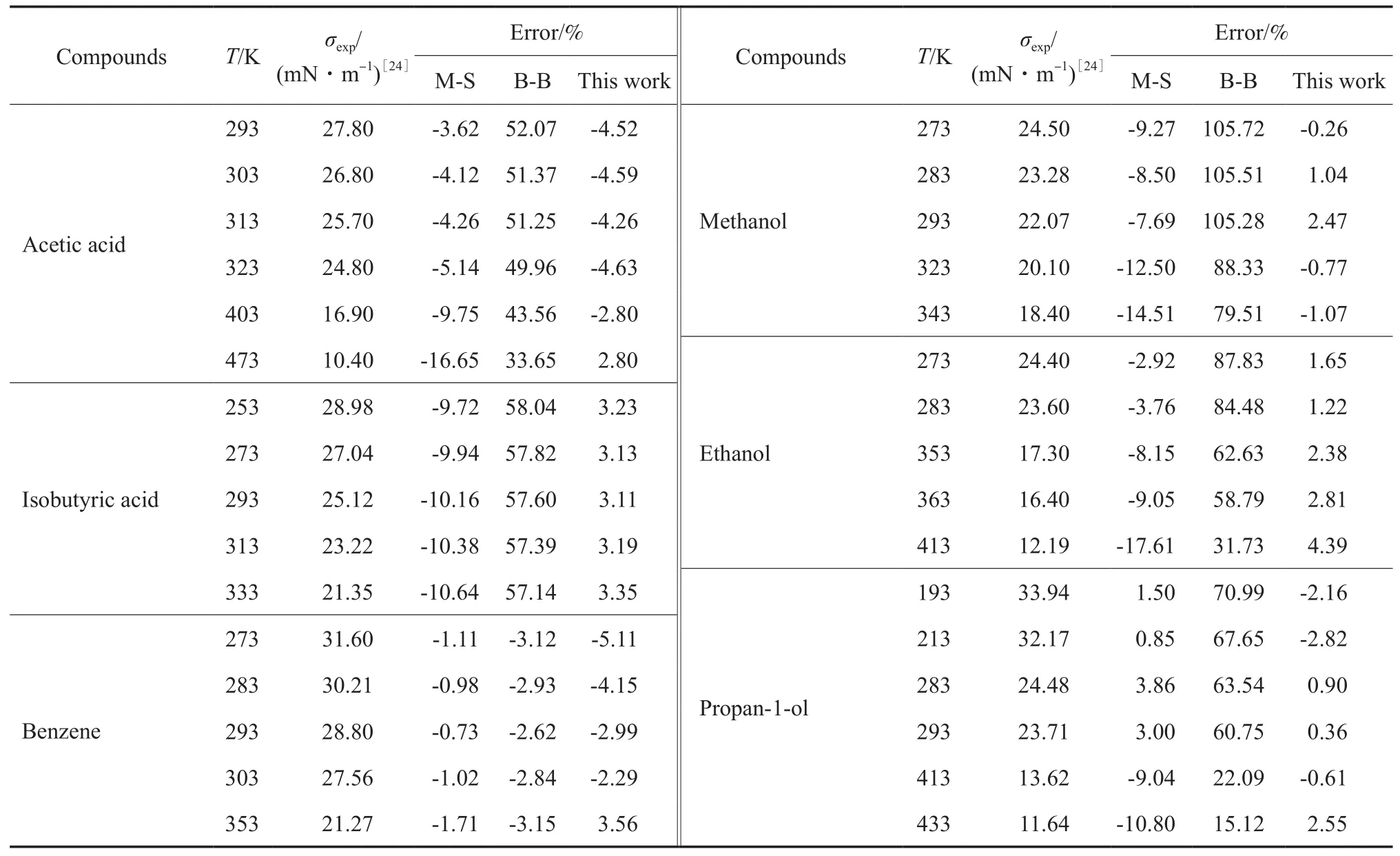
表2 本工作方程与文献方程计算结果比较Table 2 Comparison of calculated results for σ by equations of this work and literature

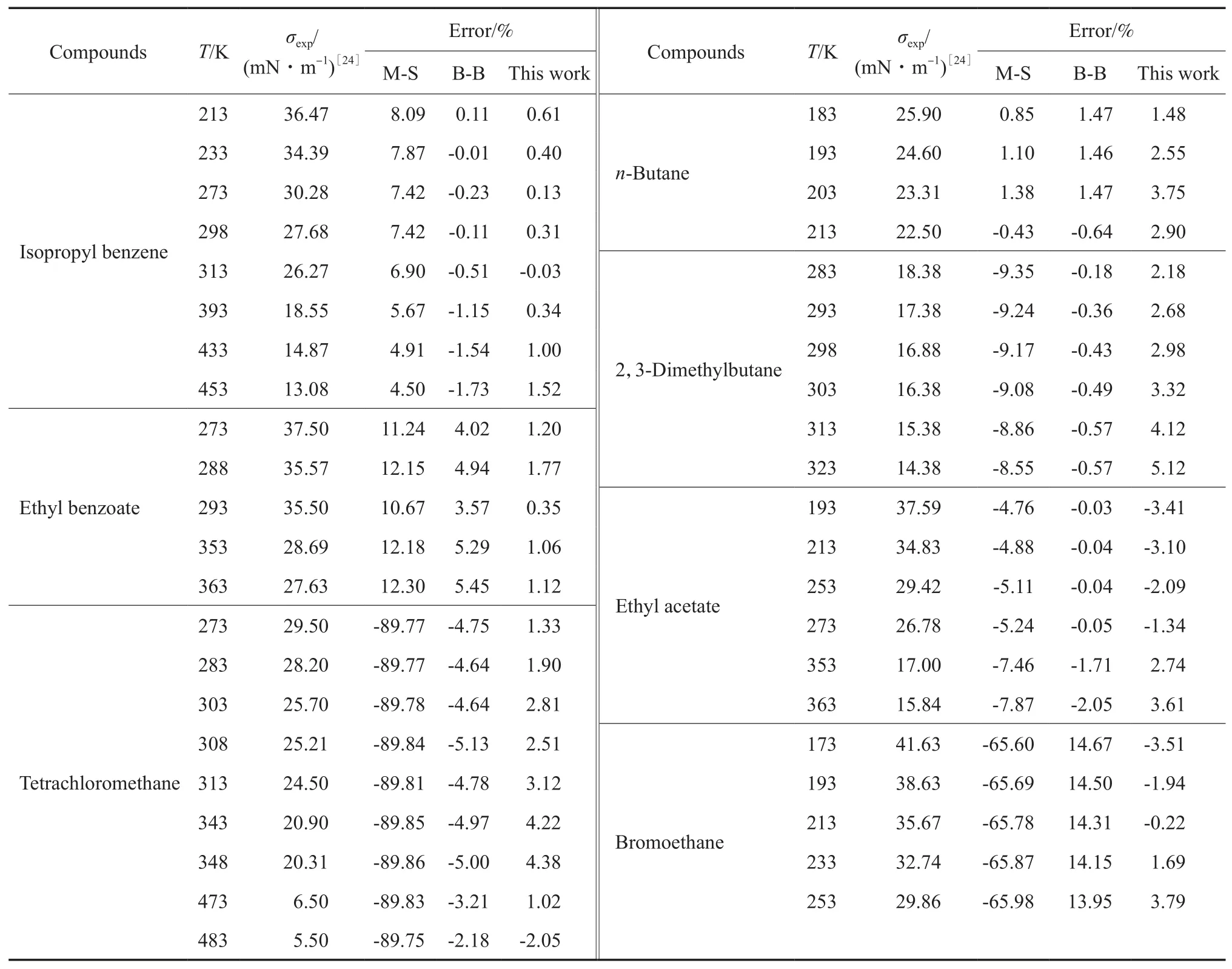
续表2

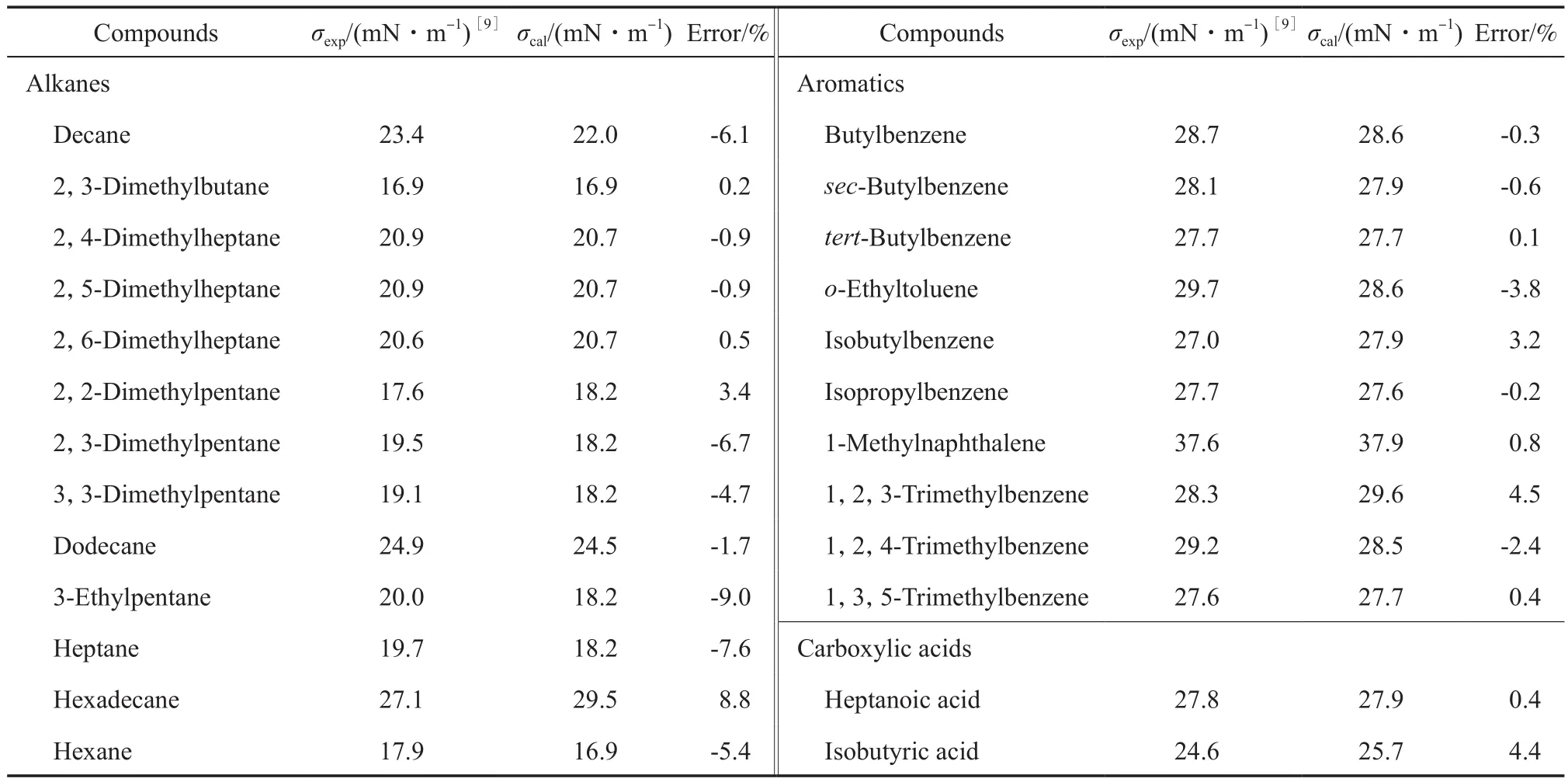
表3 298 K时有机物σ预测结果Table 3 Estimated results for the σ of various compounds by the equation of this work at 298 K

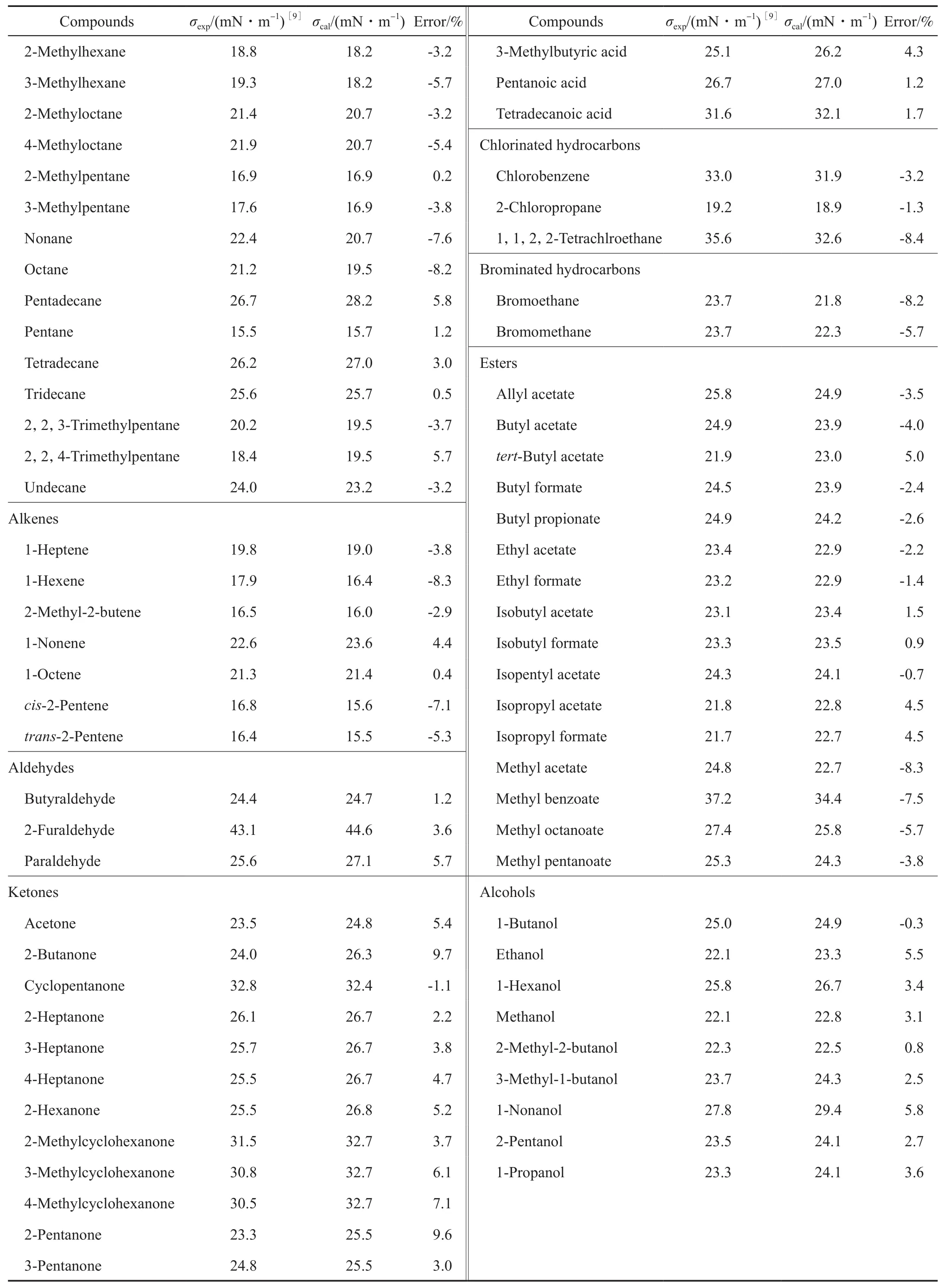
续表3

3 结论

1）提出计算σ的新方法，从本质出发，探讨了分子间相互作用、分子结构对σ的贡献，成功地将宏观物性与微观结构参数相关联，提供了架起宏观与微观桥梁的新方法和经验。

2）提出的计算σ的新方法具有坚实的理论基础，结合应用了基本的热力学公式和LSERs理论，给出的方程形式简单，方程所含参数的物理意义明确、且易于获得，计算方便、快捷，具有高的精度和良好的预测能力，可供工程设计之用。