小口径旋转稳定弹在控制作用下的弹道特性

杨 杰,谢 飞,常思江,李 响

(1.南京理工大学 能源与动力工程学院， 南京 210094; 2.辽沈工业集团有限公司 科研二所， 沈阳 110159; 3.陆军驻沈阳地区第二军事代表室， 沈阳 110159)

随着低间接伤害概率和高精度打击逐渐成为现代战争对弹箭的基本要求，常规弹箭制导化改造成为一种趋势，随即极大地促进了精确制导武器的研究进展。相比于导弹等其他制导武器，制导炮弹价格低廉，发射平台和制导机构简单，效费比较高。制导炮弹按飞行稳定方式通常分为尾翼稳定弹和旋转稳定弹，前者依靠稳定力矩保持稳定飞行，后者依靠弹体高速旋转产生较强的陀螺效应保持稳定飞行，但也使弹丸的飞行动力学特性、制导控制理论与前者有很大不同[1-3]。国外很多针对中、大口径旋转稳定弹的研究表明，作用在弹丸上的控制力可能会导致弹丸角运动不稳定[4],控制力作用的位置、大小以及持续时间不同，都会使弹丸的弹道特性有所不同[5]。

小口径旋转稳定弹相比于中、大口径旋转稳定弹，转速更高。以某155 mm榴弹和某12.95 mm枪弹为例，155 mm弹丸炮口转速约为300 r/s，12.95 mm弹丸炮口转速约为 2 400 r/s，这对控制系统提出了更高的要求。高转速使得弹丸姿态测量和执行机构动作更加困难，传感器的灵敏度要足够高，小体积和低成本以及较短的飞行时间也使控制系统的设计更加困难。

对于小口径旋转稳定弹的设计与研发，国外学者作了相当多的研究。Lawhorn等[6]发明了一种通过控制阀门开合提供控制力矩的灵巧枪弹。Barrett[7]研究了一种通过压电陶瓷材料偏转弹头提供控制力矩的身管发射式自适应枪弹。Barrett等[8]设计了一种通过压电材料形变驱动尾翼变形的灵巧枪弹。Jones等[9]设计了一种基于激光半主动制导和尾翼偏转控制的灵巧枪弹，并于2012年进行了实弹测试。James DeSpirito等[10]设计出一种称为旋转翼执行器的执行机构，以直径为3/8英寸的弹丸模型为研究对象，计算验证了其可靠的控制性能及弹丸的飞行稳定性；Boris Kogan等[11]以某12.95 mm弹丸为研究对象，通过在弹丸进动的过程中施加控制力改变弹丸的章动角，从而达到控制弹丸弹道的目的。相比之下，国内关于小口径旋转稳定弹的研究，不论是执行机构的结构、控制系统的设计，还是控制作用下弹丸的运动特性和稳定性，都比较少。

本文不考虑具体的控制执行机构，旨在分析控制作用下弹丸的弹道特性，以12.95 mm枪弹为研究对象，采用六自由度刚体弹道模型，研究了线性马格努斯力矩和非线性马格努斯力矩对弹丸角运动特性的影响，并讨论了初速和起始扰动对形成极限圆的影响。在无控计算的基础上，考虑在弹体上施加控制力和控制力矩，分析了不同初速、不同控制力作用位置下弹丸质心运动的响应特性，同时研究了控制力在不同弹道段、不同作用位置和不同方向对角运动的影响，研究结果将为后续开展小口径旋转稳定弹的控制研究提供一定参考。

1 动力学模型

为了对小口径旋转稳定弹在无控和有控条件下的弹道特性进行仿真分析，首先建立了包含有控制力和相应控制力矩项的六自由度刚体弹道方程，其中坐标系的定义见参考文献[12]。式(1)是质心运动动力学方程组，式(2)是质心运动运动学方程组，式(3)是绕心运动动力学方程组，式(4)是绕心运动运动学方程组，具体表达式如下：

(1)

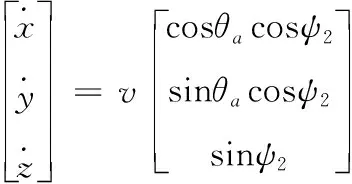
(2)

(3)

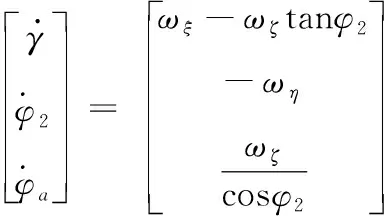
(4)

式中：v表示弹丸质心速度；θa表示速度高低角；ψ2表示速度方向角；ωξ、ωη、ωζ表示弹丸绕质心转动的角速度；φa表示弹轴高低角；φ2表示弹轴方位角；γ表示自转角；x、y、z表示弹丸质心位置；m表示弹丸质量；C表示极转动惯量；A表示赤道转动惯量。

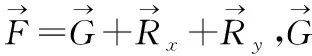
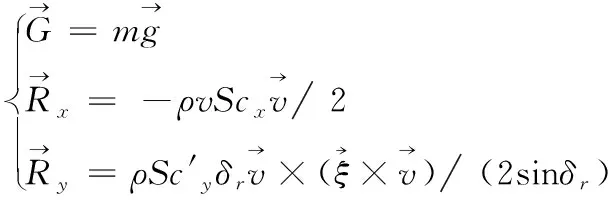
(5)

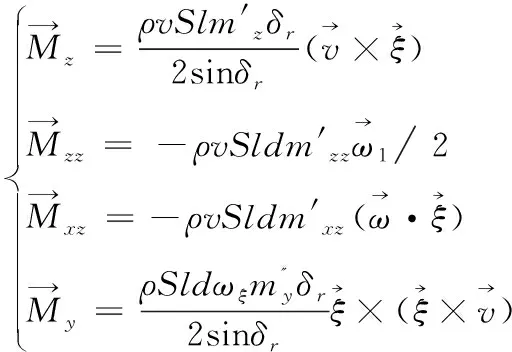
(6)

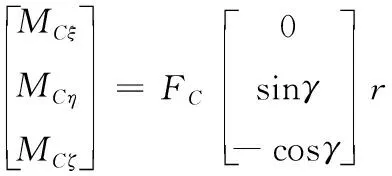
(7)

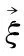
(8)

式中：cx0、cy0、mz0、mzz0、my0表示对应气动系数的线性项；cx2、cy2、mz2、mzz2、my2表示对应气动系数的非线性项。

本文以12.95 mm枪弹为研究对象，其转速极高，马格努斯力矩对弹道特性的影响较大，且非线性较强[13]。考虑到线性马格努斯力矩对弹箭动力学稳定性的影响，以及非线性马格努斯力矩对产生极限圆运动的影响[14]，因此在无控和有控条件下分析马格努斯力矩对弹丸弹道特性的影响时，参考文献[15]中所采用的研究方法，将马格努斯力矩系数的线性项与非线性项分开考虑，故将气动系数的取值分为如下4种情形，见表1。“√”表示考虑该气动系数并取文献[13]中的相应数值，“×”表示不考虑该气动系数，取0。

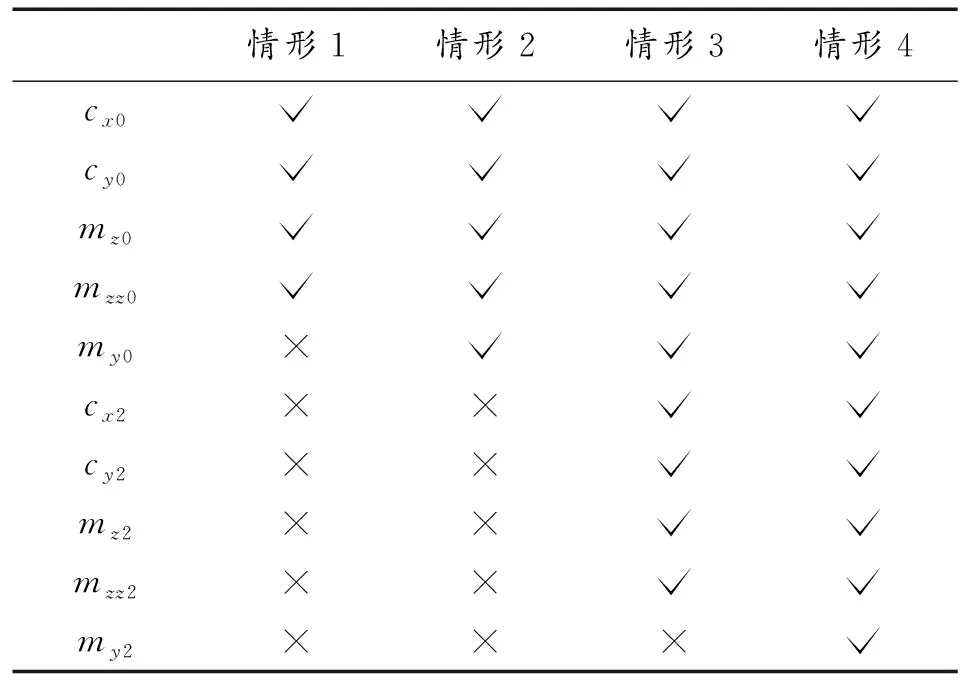
表1 不同情形气动系数取值

2 小口径旋转稳定弹的无控弹道特性

由于马格努斯力矩、马赫数等对弹丸角运动存在一定影响，从而影响弹丸的弹道特性，因此为研究控制作用对弹丸弹道特性的影响，首先取式(1)和式(7)中的控制力为0，基于不同初速，计算分析无控条件下马格努斯力矩、起始攻角和起始攻角角速度对弹丸弹道特性的影响。图1为初速为超音速条件下不同情形计算得到的攻角运动曲线。

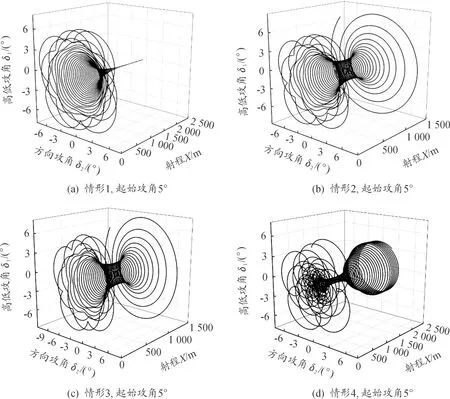
图1 超音速时弹丸攻角运动曲线

对比图1(a)、图1(b)、图1(c)和图1(d)，可见图1(b)和图1(c)攻角曲线几乎完全相同。在没有马格努斯力矩作用时，攻角随着飞行距离增加逐渐趋于0；当有线性马格努斯力矩作用时，攻角最终发散，趋于不稳定；当线性马格努斯力矩和非线性马格努斯力矩同时作用时，攻角运动最终形成极限圆。同时也可看出，线性马格努斯力矩是使弹丸不稳定的主要因素，非线性马格努斯力矩是使弹丸稳定并形成极限圆的主要因素。

弹丸在不同初速条件下，角运动会有不同特性。图2为情形4下弹丸初速在亚音速的攻角运动曲线。对比图2(a)和图2(b)可见，当初速在亚音速范围内，起始攻角为5°时，攻角运动整体上呈极限圆，但是在慢圆运动中伴随着高频的快圆运动；当起始攻角为0°时，攻角逐渐增加，不存在快圆运动，最终形成稳定的极限圆。

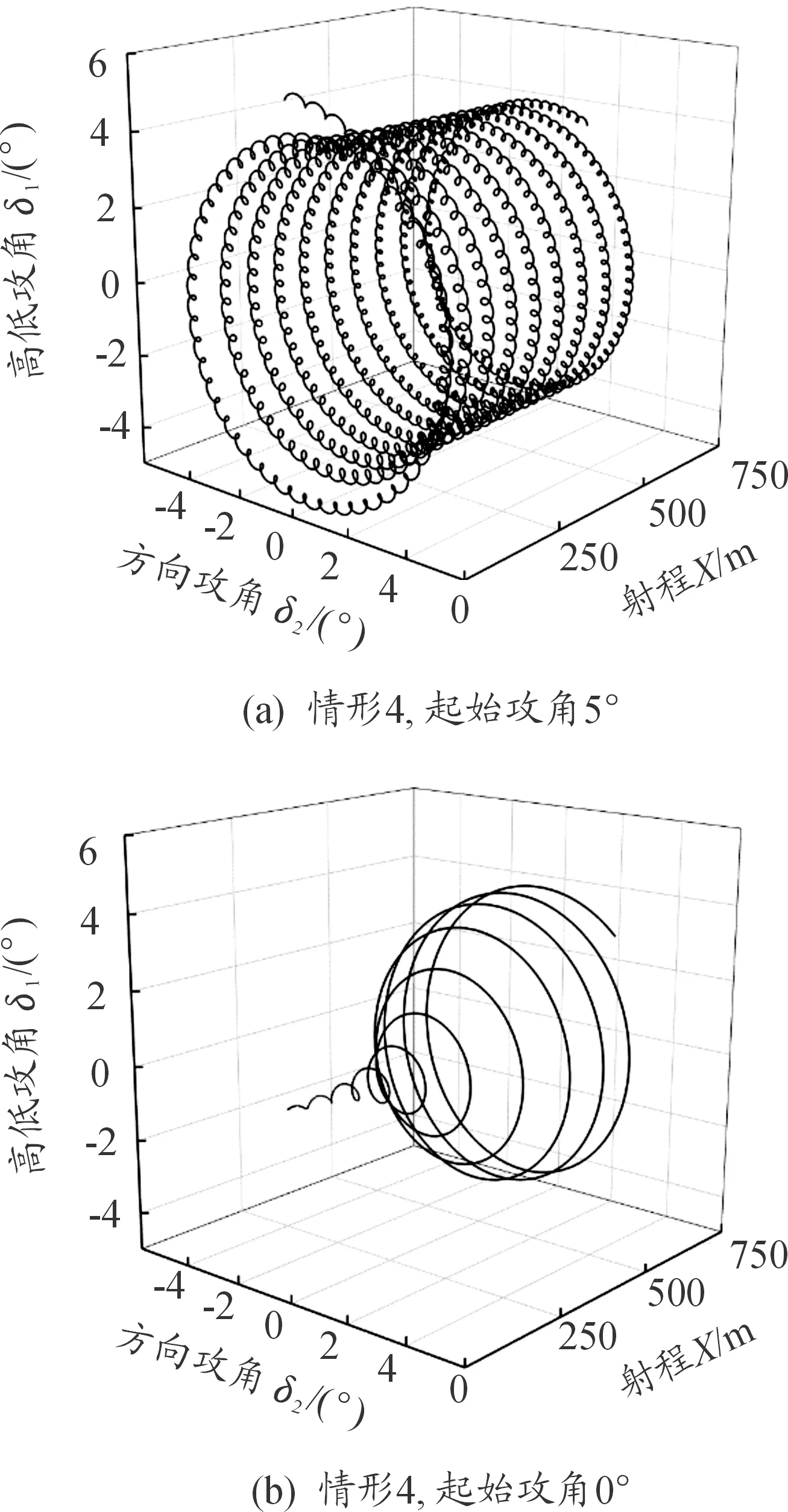
图2 亚音速时弹丸攻角运动曲线

对比图1(d)和图2(a)可见，起始攻角不为0时，在超音速条件下，起始段弹丸攻角运动中的快圆运动幅值较大，且在一个慢圆运动周期中快圆运动频率较低，随后快圆运动迅速衰减消失，慢圆运动的幅值先减小后增大，最终形成极限圆；而在亚音速条件下，慢圆运动的幅值几乎不变，其中一直伴随着高频的快圆运动，最终形成与前者情况不同的极限圆。起始攻角为0时，两种条件下攻角运动相似，如图2(b)。

由上面分析可知，弹丸初速为超音速时，起始攻角的大小对形成的极限圆没有影响；弹丸初速为亚音速时，起始攻角为0与起始攻角不为0时形成的极限圆存在明显差别。而起始攻角角速度对形成的极限圆影响很小。

3 小口径旋转稳定弹的有控弹道特性

由于小口径旋转稳定弹具有很强的陀螺效应，在某一方向上施加控制力，弹体的运动响应可能受陀螺效应的影响较大。为便于研究，参照文献[11]中的处理方法，取式(1)和式(7)中的控制力为阻力值大小的5%，基于表1的4种不同情形，计算分析不同控制力作用位置下马格努斯力矩和初速对弹丸弹道特性的影响。根据文献[12]定义弹轴系与弹体系，假设控制力与弹体固连旋转，控制力方向沿弹体系y1轴正方向，控制力示意图如图3，L表示控制力作用点与弹底的距离。这里定义弹丸在控制力作用下质心运动方向与弹轴系η轴的夹角为质心偏移方向；弹体系y1轴与弹轴系η轴的夹角定义为控制力平均方向γ；质心偏移方向与控制力方向的夹角定义为偏移角度Λ，由质心偏移方向角度减去控制力平均方向角度得到；控制力在弹丸一个旋转周期内连续转过的角度定义为控制力持续范围Φ。

图3 控制力示意图

图4为情形1、2和4下，v0=915 m/s，起始攻角5°，Φ=90°，γ=0°，FC=5%Rx，控制力作用在不同位置时，偏移角度Λ随L的变化曲线。由图4可知，在3种情形下，随着L从d变化到4d，Λ从接近0的负值逐渐增加，在L=3d附近为正值，变化较为平缓，在L=3d～3.5d之间，Λ陡增到接近180°，随后缓慢增加。在同一作用位置时，3种不同的情形对应的Λ值也有所差异。

图5为情形4下，起始攻角5°，Φ=90°，γ=0°，FC=5%Rx，初速不同时Λ随L的变化曲线。由图5可见，初速越低，Λ由负值变为正值变化点L越大，Λ增大到180°越缓慢，曲线变化越平缓。v0=915 m/s时压力中心距弹底约2.99d，v0=600 m/s时压力中心距弹底约3.15d，v0=300 m/s时压力中心距弹底约4.58d，结合图5可见该变化点与弹丸的气动压力中心位置相关。当控制力作用在压力中心之后，Λ为负值；作用在压力中心时，Λ为0；而作用在压力中心之前，Λ变为正值，且距压力中心越远Λ越接近180°。

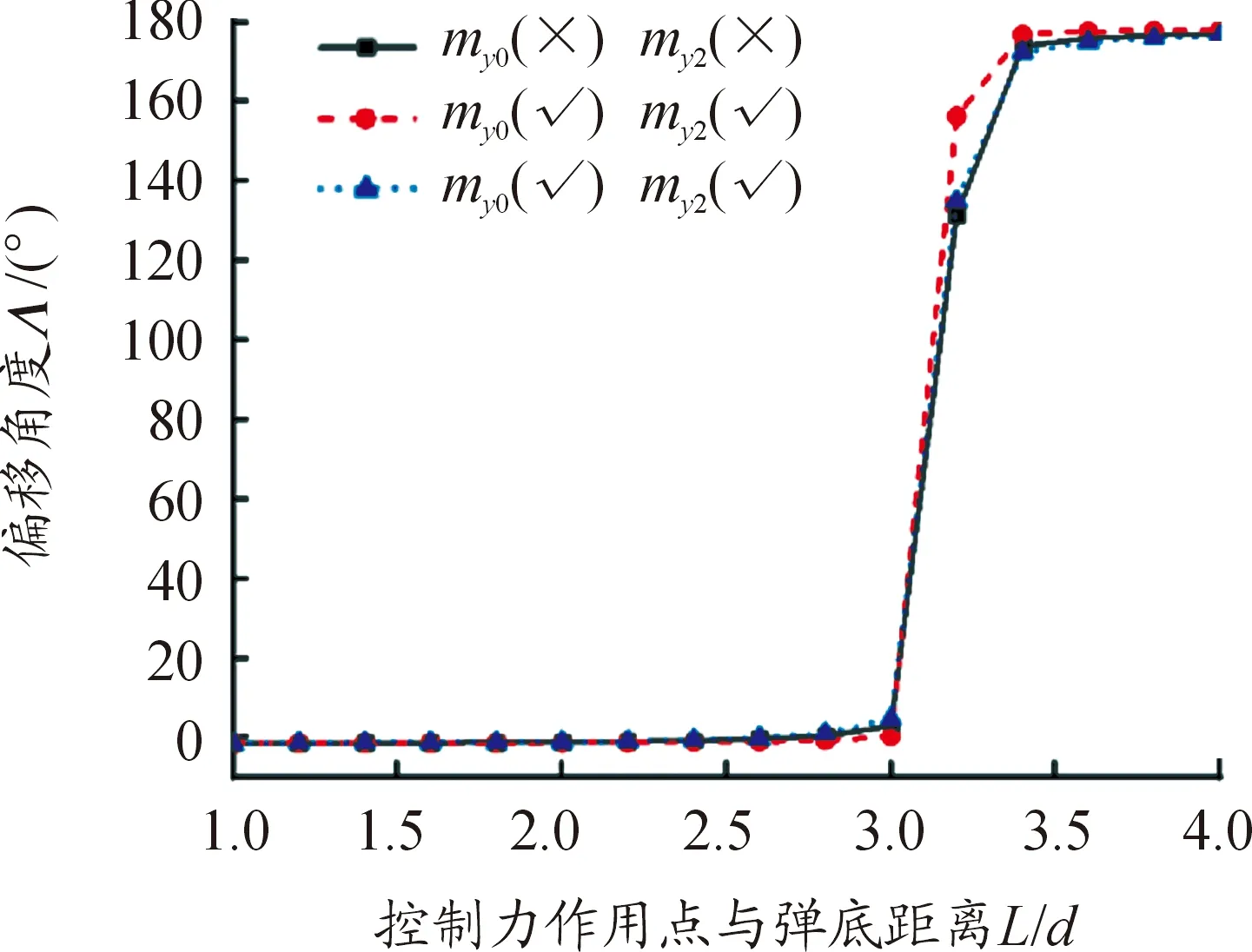
图4 3种情形下Λ随L变化曲线

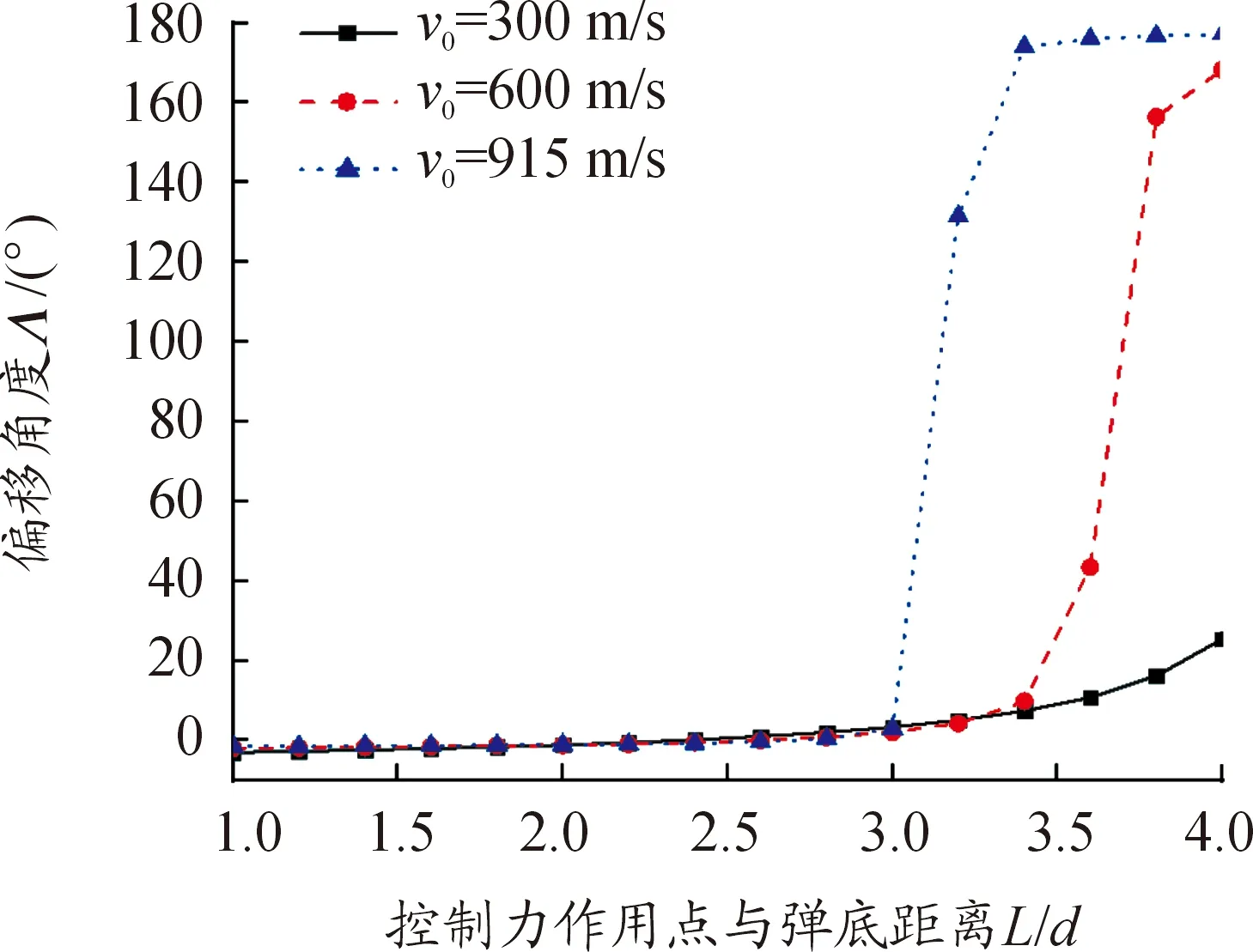
图5 初速不同时Λ随L变化曲线

在分析了质心运动在控制力作用下的响应特性之后，进一步分析角运动在控制力作用下的响应特性。计算条件为情形4下，v0=915 m/s，起始攻角5°，Φ=90°，FC=5%Rx，图6为在弹道段x=2 100～2 200 m，γ=0°，控制力作用在不同位置时攻角曲线。图7为在弹道段x=700～800 m，控制力作用在L=d，控制力向不同方向作用时攻角曲线。

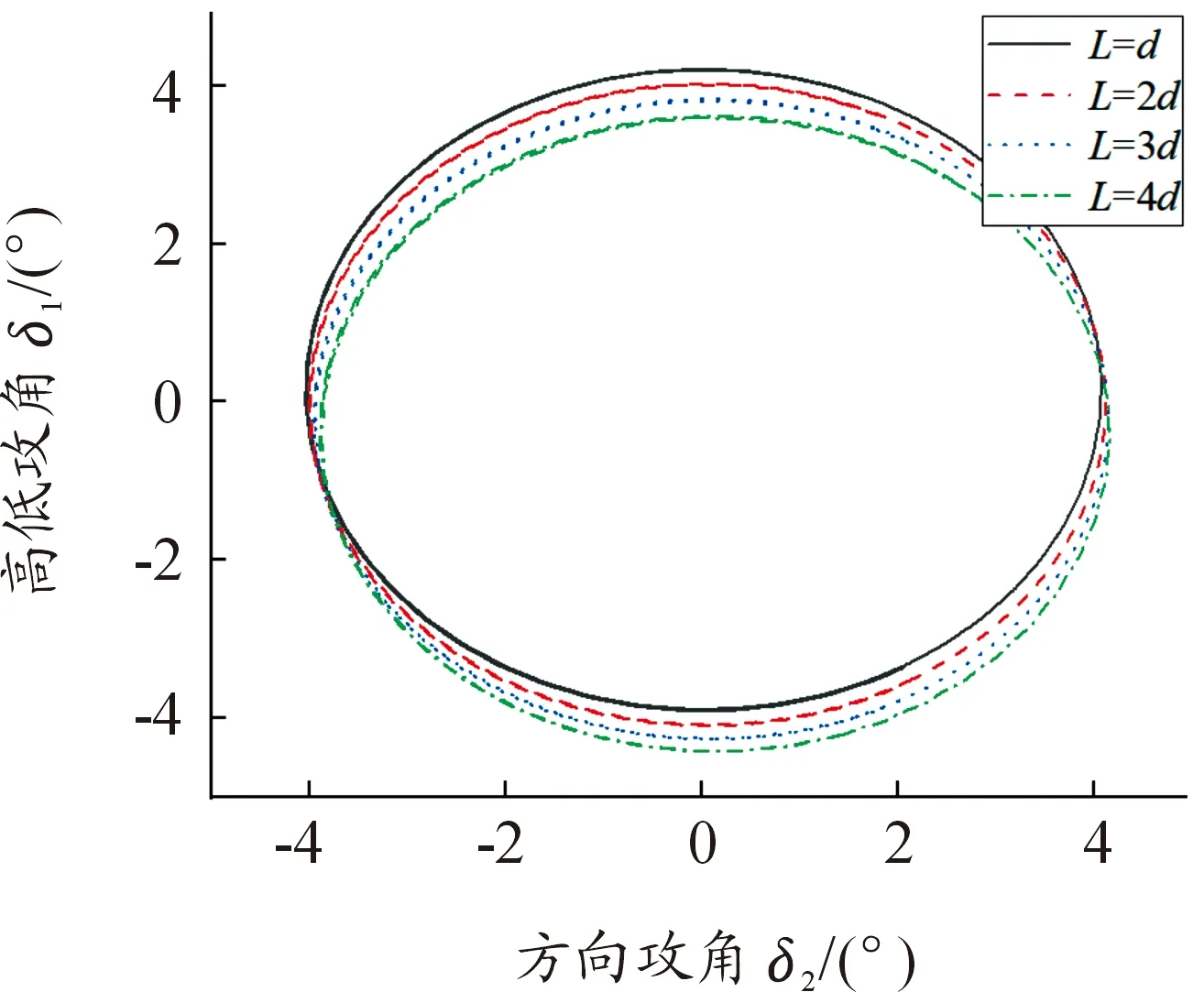
图6 L不同时攻角曲线

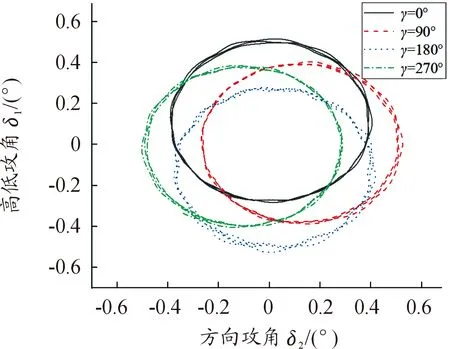
图7 γ不同时攻角曲线

由图6可知，当控制力作用位置从L=d变化到L=4d，控制力作用点从弹丸质心之后逐渐移动到质心之前，攻角逐渐减小。由图7可知，当控制力作用方向为γ=0°时，攻角曲线也向γ=0°方向附近变化，随着γ改变，攻角曲线也依次向对应方向改变，且慢圆运动中包含有幅值较小的快圆运动。对比图6和图7可知，当控制力作用在质心后，随着控制力作用方向变化，攻角曲线向与控制力相同的方向变化；当控制力作用在质心之前时，攻角曲线则向与控制力相反的方向变化。

图8为情形4下，在弹道段x=700～800 m，v0=915 m/s，起始攻角5°，Φ=90°，γ=0°，L=d，FC不同时弹丸的攻角运动曲线。由图8可知，在控制力作用下，攻角运动产生了幅值较小的快圆运动，而且控制力越大，攻角越大，同时快圆运动的幅值越大。结合图6、图7和图8可知，在形成极限圆之前的弹道段，控制力作用会使攻角在慢圆运动中产生快圆运动，而在已经形成极限圆的弹道段，攻角运动在控制力作用下则无明显变化。

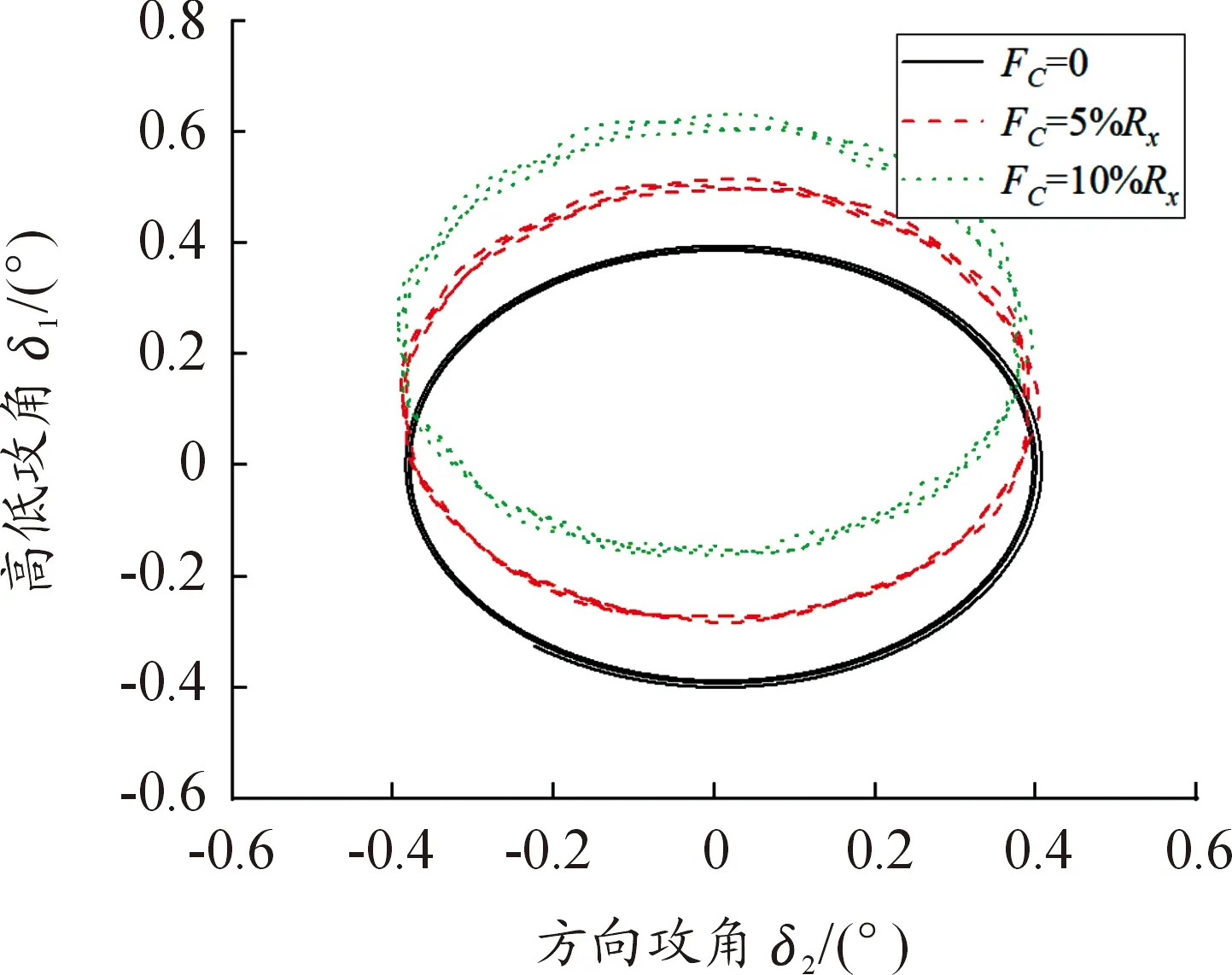
图8 FC不同时攻角曲线

4 结论

1) 无控条件下，初速为亚音速时形成的极限圆受起始攻角影响很大，而初速为超音速时形成的极限圆则受起始攻角影响很小；

2) 有控条件下，不同初速条件下弹丸压力中心位置不同。随着控制力作用点改变，控制力作用在压力中心后，质心运动与控制力同向；控制力作用在压力中心前，质心运动与控制力反向。随着控制力作用方向变化，控制力作用点在质心后，攻角运动向相应的方向变化，作用点在质心前，攻角运动则向相反的方向变化；

3) 在极限圆形成之前，控制力使攻角在慢圆运动中产生了高频的快圆运动；控制力越大，攻角变化越大，快圆运动的幅值越大。在极限圆形成之后，控制力对攻角运动无明显改变。