测压试验数据处理中两种分块积分法的对比分析

潘伟 徐凯铭 虎小明

摘要：风洞测压试验数据是载荷设计依据，在风洞试验数据可靠的情况下，如何去处理试验数据得到更准确的处理结果，将直接影响着后续的全机载荷设计结果。在试验数据处理的时候，我们使用的都是用分块积分法，由于试验模型大小的限制，在模型上布置的测压点数量有限，因此如何根据测压点的位置进行分块是其中的关键，这不仅影响到最后计算的载荷结果的准确性，还影响到最后强度校核时的加载结果。

关键词：测压数据处理;分块积分法;分块方法

1 概述

载荷是飞机结构设计的原始输入，载荷的准确性就直接影响着飞机结构的可靠性，载荷输入越准确，就能设计出更加合理可靠的机体结构，便可以有效的减轻机体结构的重量，提高飞机的飞行性能。载荷设计的常用方法是进行风洞测压试验，风洞测压试验的数据作为载荷设计依据，这是最可靠的方法。那么在风洞试验数据可靠的情况下，如何得到更加精确的的载荷就是作为一名载荷设计人员需要关注的问题。

本文将两种不同的分块积分法得到的测压试验数据处理结果与部件测力试验数据的结果进行对比来分析两种方法的准确度。

2 分塊积分法

2.1 二维平面分块积分法

二维平面分块积分法，以侧向力系数处理为例：

第一步，分块：

取所计算部件的侧向投影，首先将相邻测压剖面按照平面距离的中间位置分割，再将相邻的测压点进行连线，然后取相邻直线的中点再次连线，这些中点之间连线与剖面分割线将侧向投影分成n个微元（n为测压点的个数），然后取出这些块的面积Si，以及质心坐标Xi，Yi;

第二步，积分：

上述式中的为参考面积。

2.2 三维分块积分法

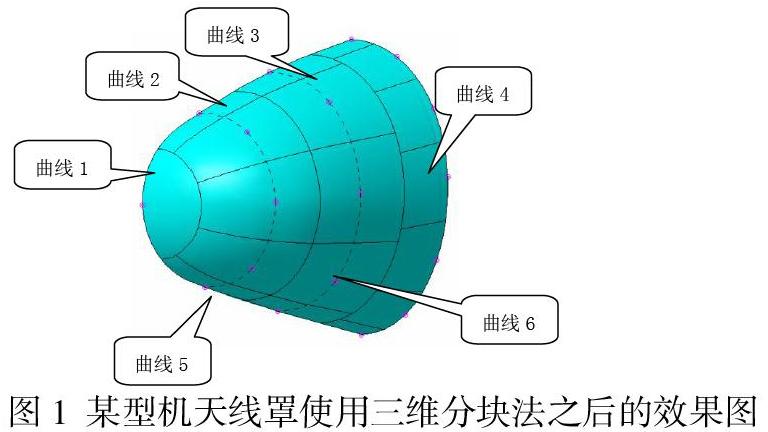
介绍在三维数模上分块方法时以某型机天线罩为例，在进行风洞试验时，该天线罩上共有4个测压剖面18个测压孔，每个测压剖面上的测压孔数量如图1所示，分别为1个、5个、5个和7个，其中2、3、4剖面的测压孔都在同一个平面上。

首先第一剖面的唯一一个测压孔与第二剖面的第三个测压孔之间做直线，再将这条直线法向投影到天线罩上得到一条曲线，取这条曲线的中点，以及第一剖面的唯一一个测压孔与第二剖面第一点和第五点之间的两条曲线的中点，由着3个点确定一个平面，然后取这个平面与天线罩的交线（曲线1）作为第一剖面和第二剖面之间的分割线，同理分别作出曲线2和曲线3作为另外两条剖面之间的分割线。取出第二、第三测压剖面测压孔所在平面与天线罩的交线曲线5和曲线6，再取第二、第三剖面各自的第一和第二测压孔之间的曲线的中点，在然后用这两个中点和第一剖面的测压孔确定的平面与天线罩的交线作为第二和第三剖面的第一和第二测压孔对应块的分割线;同理可以作出第二和第三剖面其它测压孔对应块的分割线。取出第四剖面各相邻测压孔之间曲线的中点，然后按这些中点在曲线4的比率投影到曲线3上，再作出这些中点与对应投影点的连线，再将连线法向投影到天线罩上，投影得到的曲线即作为第四剖面测压孔对应块之间的分割线。最后作出模型的三向投影，取出各向分块对应的面积和质心。

上述在三维空间分块时作分割线的方法不一定固定，但效果近似即可。

2.3 两种分块方法得到分块结果比较

比较两种方法的分块结果时以图1中的天线罩为例，图2～图4为两种分块方法分块后的效果图，从图2～图4中可以看出，各测压孔对应块的差别明显，对各个块的面积及质心有着显著的影响。

以该天线罩的航向投影面积为例，表1是取出图2中两种分块结果的航向投影面积，从表中可以发现各个块的面积均不相同，且绝大多数微元的面积有较大的变化。由于在同一个状态下，各个测压孔的压力系数Cpi是相同的，同时在计算力系数的时候使用的参考面积也是相同的，则从式（1）可以看出只有分块的面积Si会影响到力系数的最终计算结果，而从式（2）和式（3）中可以发现，天线罩的压心坐标受各个块面积的影响，还受到各个块的质心的影响，在本文中暂不讨论各个块的质心对天线罩压心坐标的影响。

3 两种分块积分法对最终结果及强度校核加载的影响

3.1两种分块方法对最终结果影响的比较

为了分析两种分块方法对最终积分结果的影响，还是以上面提到的天线罩为例，利用数值模拟计算了该天线罩在不同状态下的三向力系数，并取出表1中对应测压孔的压力系数Cpi ，然后按照两种不同的分块结果进行积分求出相应的力系数。

从图5中可以看出，两种分块方法处理得到的三向力系数都与真实结果在规律上保持了一致，但是使用三维分块积分法处理得到的三向力系数更加接近部件测力的试验结果，这说明使用三维分块积分法来处理风洞测压试验数据，能够有效的提高载荷的准确度。

从两种分块积分法的分快处理方法上来看，二维分块积分法对同一个部件需要进行三次分块处理，如果将三次分块的边界线从二维平面反推回到三维空间，会发现三次的分块是完全不一样的，而对于同一个模型上的测压点来说，这样的做法是不应该的，对于三向力系数来说所对应的微元应该是不变的，而三维分块积分法同一个部件只进行了一次分快处理，每一个测压点所对应的微元保持不变，在处理方法上更为合理。

前面提到的都是在外形相对比较规则的模型上进行，如果模型外形不够规则，有明显的拐角，或者局部曲率过大，这时候分块就不能直接用中点间的连线来分块，必须要考虑拐角和大曲率的区域，这时候如果继续选择在二维模型上进行分块，最后的载荷准确性就会大大的降低，而在三维模型上分块，就可以更加合理的对拐角和大区率区域进行分块。

4 结论

通过前文中的分析和对比结果，不难发现，在测压数据处理时进行分块积分之前，对模型进行合理的分块很重要，相比于二维分块积分法，采用三维分块积分法在三维模型上进行分块，第一，分块结果会更加合理，特别是对有大曲率变化的以及有拐角的不规则曲面，能够有效的规避不合理甚至是错误的分块;第二，最终的测压数据处理结果会更加准确，这个准确将不只是体现在力系数上，合理的分块，最终计算出的压心也会更加准确。

总的来说，测压数据处理时采用三维分块积分法，能够有效的提高载荷的准确性，为飞机结构设计提供更加准确的载荷输入，有助于设计出更加合理可靠的机体结构。