桥梁健康监测2019年度研究进展

单德山 罗凌峰 李乔

摘 要：橋梁健康监测系统利用通信传感设备远程记录运营中的结构持续响应，通过对信号数据的处理分析实现桥梁结构的实时预警与安全评估，从而达到保护结构正常运营、延长结构使用寿命、指导桥梁结构管养与维护决策的目的。桥梁健康监测技术作为桥梁工程领域新兴的分支，已逐渐成为一个热门研究方向。为了促进该领域研究进一步发展，指导健康监测系统在桥梁工程中更高效地应用，对桥梁健康监测系统的实施决策、传感器信号预处理、信号数据降噪处理、模态参数识别、有限元模型修正、损伤识别、状态预测与评估等关键技术方法的研究现状进行了详细介绍，并对2019年度内相关研究进展及应用进行了总结与评述，最终发现模式识别技术与机器学习方法正越来越广泛地应用到桥梁健康监测的研究中。

关键词：桥梁健康监测系统;信号预处理;模态参数识别;有限元模型;损伤识别

中图分类号：U446.2   文献标志码：R   文章编号：2096-6717（2020）05-0115-11

收稿日期：2020-04-04

基金项目：国家自然科学基金（51978577、51678489）;国家重点研发计划（2016YFC0802202）;国家重点基础研究发展计划（2013CB0363）;中电建路桥集团资助科研项目（SCMQ-201728-ZB）

作者简介：单德山（1968- ），男，教授，博士生导师，主要从事桥梁健康监测理论研究，E-mail：dsshan@163.com。

Received：2020-04-04

Foundation items：National Natural Science Foundation of China （No. 51978577， 51678489）; National Key R&D Program of China （No. 2016YFC0802202）; National Key Basic Research Program of China （No. 2013CB0363）; Science and Technology Project of Power China （No. SCMQ-201728-ZB）.

Author brief：Shan Deshan（1968- ）， professor， doctorial supervisor， main interest： bridge health monitoring， E-mail： dsshan@163.com.

Abstract： The bridge health monitoring system （BHMS）continuously measures and records the structural responses by using a variety of sensors and communication devices in the bridge operation process. The automatic analysis of signal data can be done effectively in the BHMS to fulfill the timely danger warning and safety assessment.So as to protect the normal operation of the structure， prolong the service life of the structure， and guide the management and maintenance decision of the bridge structure.As a new branch of bridge engineering， bridge health monitoring technology has gradually become a hot research field. For the sake of the more efficient application of health monitoring system in bridge engineering， this paper summarizes the current states of several representative BHMS techniques： the decision-making analysis for the BHMS implementation， sensor signal preprocessing， signal de-noising processing， modal parameter identification， finite element model updating， damage identification， condition prediction and assessment. Then， the related researches and applications of these key techniques during 2019 are summarized and discussed.Consequently， it is found that the pattern recognition technology and the machine learning method are more and more widely used in the current research of bridge health monitoring.

Keywords：bridge health monitoring system（BHMS）; signal preprocessing; modal parameter identification; finite element model; damage identification

桥梁结构健康监测系统通过通信传感设备实时自动采集运营桥梁的响应信号，即车辆荷载、风荷载、温度荷载、环境随机振动下结构的各种真实响应;然后采用数学与计算机方法[1]分析处理信号数据，得到各种结构响应的特征值和阀值，如模态频率、阻尼比、最大位移值、最大应力值等;再将测得的这些关键数值与相应设计限值比较，作为桥梁结构实时预警与安全状况评定的依据，进而为桥梁管养维护提供决策。因此，中国已有不少大跨复杂桥梁结构都安装有健康监测系统，如苏通大桥、虎门二桥、润扬大桥、港珠澳大桥、青马大桥等。

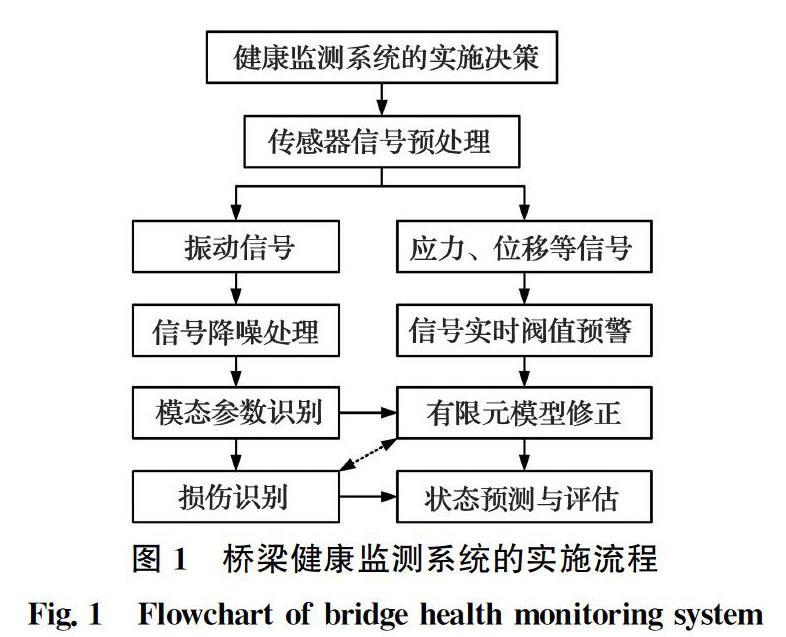
桥梁健康监测系统每天会连续产生大量的信号数据，面对海量的监测数据，有必要采用合理的处理手段从中分析出有价值的信息，为桥梁结构实时预警与运营状态评估提供重要的科学参考依据。因此，当设计、实施并调试完成一个桥梁健康监测系统的硬件部分后，应首先采用传感器信号预处理技术实现海量信号的存储，再识别、恢复由传感器故障引起的异常信号。然后，对预处理后的振动信号进行降噪处理，对降噪后的振动信号进行模态参数识别，所得结构参数用作后续有限元模型修正与损伤识别的输入;对预处理后的应力、位移等非振动信号进行实时的预警运算，判断其是否超过设计限值、是否符合修正后有限元模型的结构预测值。通常，可以通过修正后的有限元模型得到桥梁损伤识别所需的训练样本，而损伤识别结果反过来又可以实现子结构的有限元模型修正（即实现构件层面的模型修正）。最后，根据修正后的有限元模型与损伤诊断结果评判桥梁结构的安全状态。因此，传统的桥梁健康监测系统实施流程如图1所示。

研究大跨桥梁健康监测系统的主要目标是积累桥梁健康监测的设计和科研素材，实现结构实时损伤诊断与安全评估，最终支撑管养决策。现阶段，桥梁健康监测的技术难点与研究热点主要是：1）健康监测系统的决策与设计;2）传感器信号预处理;3）信号数据降噪处理;4）模态参数识别;5）有限元模型修正;6）损伤识别;7）状态预测与评估。

1 健康监测系统的决策与设计研究

在桥梁管养维护中，传统的人工检测方法因其固有的滞后性和低效性，造成桥梁运营成本的提高和资源配置的不合理，已跟不上桥梁发展的形势。为保证桥梁结构的正常运行，桥梁健康监测系统的研究与应用已经越来越受到重视。然而，具体某座桥梁结构是否需要设计安装健康监测系统，应与人工巡检等其他管养方案进行比较，根据各项风险概率来综合评估其全寿命周期内的整体运营成本。

2005年至2015年，Gatti[2]相继对意大利10家从事桥梁动载试验的工程公司进行采访，采访涉及到100座不同类型的桥梁，其中，29座是钢筋混凝土桥梁，35座是预应力钢筋混凝土桥梁，22座是钢桥，14座是钢混组合桥梁。统计结果表明，抽样调查的全部桥梁在这十年内经历的所有动载试验中，识别到的模态数量均从未超过5阶。然而，与动载试验相比，桥梁健康监测系统实时采集并能识别到的模态频率与模态振型通常不低于8阶;笔者正在参与实施的重庆某山区大跨悬索桥健康监测系统，平均每次识别到的模态数量不低于12阶。若识别到的参数数量不够，将不利于后续的有限元模型修正、桥梁损伤诊断和结构状态安全评估等重要分析工作的可靠性。由此可见，定期的桥梁动载试验除了不具备实时监测、分析和评估的功能之外，也未能达到桥梁健康监测系统的识别精度与评判准确性。

虽然桥梁健康监测系统比定期动载试验具备更强的参数识别能力，但要真正实施桥梁健康监测系统还需证明其经济效益的正当性。Neves等[3]依据决策树模型方法提出了一种决策桥梁健康监测系统实施与否的动态框架，该框架应用贝叶斯方法修正最优决策，力图在不危及安全的前提下实现更大的整体经济效益，然后以一座实际桥梁为例，依据不同桥梁状况下各种事件概率和相关费用展开了最优化桥梁健康监测系统决策。Neves等提出的决策方法具有一定的潜力与可行性，但在使用贝叶斯方法修正最优决策的过程中，引入的输入参数及其组合仍然偏少;因此，该方法具有一定的局限性，还需进一步研究。然而，该方法至少证明：如果结构的管理规划执行合理，那么，对于节省桥梁整体运营成本并延长其使用寿命这个终极目标而言，对健康监测系统的投资仍是值得尝试的，桥梁健康监测技术仍是值得研究的。

决定实施健康监测系统后，需要针对桥梁结构的具体情况设计合理的健康监测系统。陈华等[4]针对小河特大桥的结构特点，为保证结构安全服役和危险状态预警而设计了该桥的健康监测系统，由于需要重点关注该钢管拱桥的主拱应力，因此，选择了应用较成熟的光纤布拉格光栅（FBG）应变传感器和钢弦应变计布置在钢管拱肋上;此外，还选取了高清摄像仪、光纤光栅表贴式传感器等常规传感器用于监测该桥的变形状况与环境温度场，最后通过通用数据采集仪、光纤光栅解调仪和振动信号采集仪等采集组网设备集成了小河特大桥健康监测系统，提出了一套适用于公路钢管拱桥的健康监测系统设计方案。顾津申[5]针对石济黄河公铁两用桥的结构特点及运营养护维修特点，同时考虑了静态及动态监测指标，在主桥上布置了风速风向仪、温湿度计、应变计、振动位移计、加速度计、高清摄像机、倾角仪等共计13类、157个高精度传感器，并阐述了相关硬件设备的选型标准、布置原则，然后采用光纤组网和互联网交互的方式集成了该桥的健康监测系统，最终提出一套适用于高速铁路桥梁的健康监测系统设计方案。

2 传感器信号预处理研究

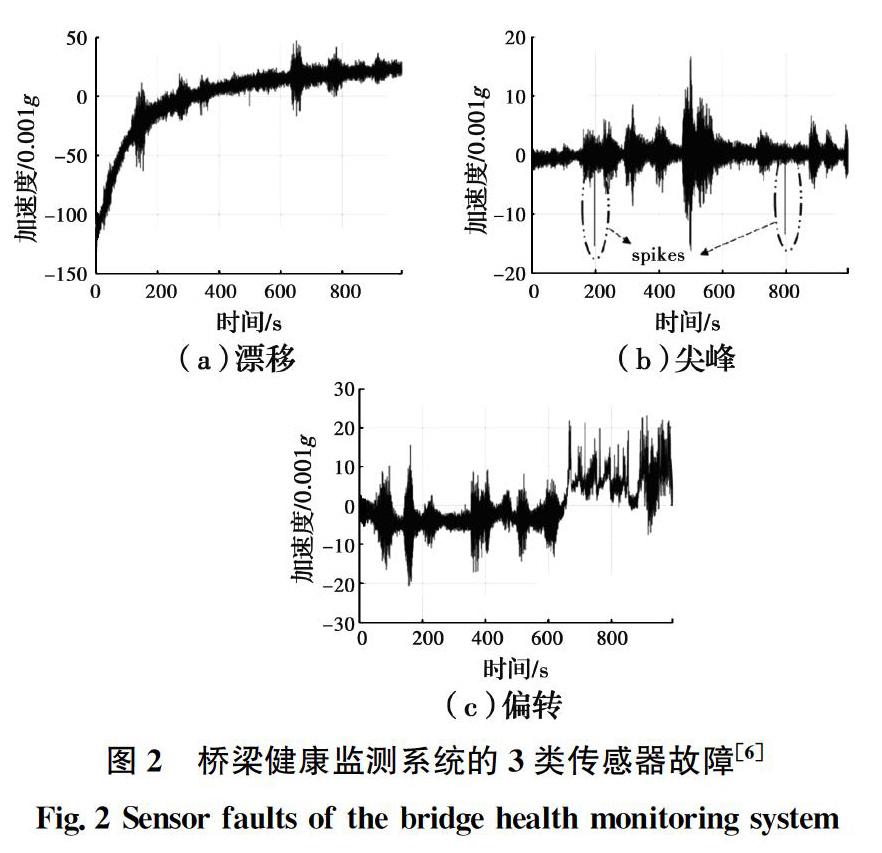
桥梁健康监测系统使用中，传感器设备故障时有发生，硬件设备故障导致的信号数据异常往往会降低计算分析的准确性，导致桥梁健康监测系统无法实现其自动化监测和状态评估的职能。信号预处理技术用来存储传感器采集得到的海量信号，并识别、检测和恢复传感器故障引起的异常信号。桥梁健康监测系统采集到的振动信号因传感器故障而出现数据异常时，可分为漂移、尖峰和偏转3种类型。这3类故障在加速度信号时程图中的表现形式如图2所示[6]。因此，为了更好地为桥梁安全评估提供依据，应首先评判传感器信号质量，识别发生故障的传感器;当识别到系统某测点处传感器输出信号異常之后，如何将异常数据“变废为宝”就显得非常重要，其相关研究还尚少。

为解决传感器故障引起的信号数据异常问题，Fu等[6]提出了一个3阶段策略：首先，采用分布式相似性测试方法（Distributed similarity test），根据各测点信号功率谱密度的相似性来检测传感器是否故障;然后，通过训练人工神经网络（ANN）来识别传感器故障类型;最后，直接使用估计值或采用校正函数（如均值处理、平滑趋势项处理等）来替换故障数据，并恢复因传感器故障而呈现数据异常的那部分信号。在该研究中，Fu等对金东大桥健康监测系统测得的历史振动信号数据展开了统计研究，分析了3类传感器故障对信号数据分析结果的影响，并提出了一种非常有效的故障数据恢复策略，该策略包括故障检测、故障识别和故障恢复。

向阳等[7]提出了一种基于K线图时间片驱动的滑动窗口数据流处理模型，完成了桥梁健康监测信号的海量数据压缩存储。Ni等[8]基于深度学习理论中的大数据压缩与重构技术，提出一套更为完整的传感器信号预处理方案：首先，采用一维卷积神经网络（CNN）直接提取传感器信号的特征，实现异常数据的高精度检测识别;然后，基于自编码器（AE）提出了一种传感器信号的数据压缩与重构方法，保证传感器信号数据经过大幅压缩存储后，再实现高精度的数据重构恢复。该研究采用某大跨悬索桥健康监测系统的振动信号数据，验证了这项传感器信号预处理技术的有效性。

3 信号数据降噪处理研究

运营桥梁的健康监测系统不间断地传输信号数据，由于野外实测信号存在复杂噪声，因此，仅对信号预处理后仍不能直接进行识别分析，还应对信号进行降噪处理。现阶段，信号降噪处理方法分为滤波和分解重构两种。滤波处理通常只能完成实验中模型桥振动信号的降噪工作，无法较好地剔除野外桥梁实测振动信号中的复杂噪声。因此，信号分解重构技术近年来广泛应用于桥梁健康监测信号的降噪处理，并展现出良好的性能。目前，信号数据降噪处理研究主要集中在小波变换法（WT）、经验模态分解法（EMD）及其结合方法的改进上。

严鹏[9]在传统EMD小波阈值降噪算法的基础上，提出一种改进EMD小波相关降噪算法，该算法综合了EMD、WT和相关检测3种方法的优点，适用于桥梁健康监测信号的降噪處理。陈永高等[10]将多元统计学中的“解相关算法”和“谱系聚类”引入了集合经验模态分解算法（EEMD）中进行改进，避免了模态混叠现象，并构建了用于筛选有效本征模态函数（IMF）的新指标以实现其智能化筛选。刘欣悦等[11]针对近断层地震脉冲信号具有非线性非平稳的特点，提出了一种改进的互补集合经验模态分解算法（CEEMD），并将该算法应用于实桥信号降噪处理，效果良好。Huang等[12]提出了一种将熵置换、谱代换和EEMD算法相结合的方法，简称PSEEMD;通过对武汉白沙洲长江大桥实测振动信号进行降噪处理，证明该算法能解决模态混叠问题，能有效抑制噪声，能从强噪声中有效提取原始信号的高频特征。

张二华等[13]针对桥梁结构动力测试信号易被强噪声淹没、非线性非平稳检验困难的问题，将改进的集合经验模态分解算法（IEEMD）、递归图理论（RP）和递归量化分析（RQA）相结合，提出了一种针对振动信号的多尺度非线性非平稳检验分析方法，最终证明所提方法可用于实际桥梁测试信号的非线性非平稳检测。在此基础上，张二华等[14]针对桥梁非线性非平稳信号，又采用了多种时频域降噪处理方法，对某大跨斜拉桥的实测振动信号进行了降噪效果对比，研究结果表明：与EMD法、EEMD法和经验小波变换法（EWT）等传统方法相比，变分模态分解法（VMD）具有更强的降噪能力。

4 模态参数识别研究

在桥梁健康监测中，结构的模态参数识别通常颇具难度。桥梁结构的模态参数主要是指结构的频率、振型和阻尼比，它们反映了结构的系统特性。针对桥梁运营中的环境激励，研究者们已经提出多种较成熟的运营模态分析方法（OMA），例如随机子空间法（SSI）、环境激励法（ERA）、频域分解法（FDD）、峰值拾取法（PP）、随机减量法（RDT）、时域参数识别法（ITD）等。上述OMA方法又可以分为频域方法（FDD、PP）和时域方法（SSI、ERA、RDT、ITD）。频域方法通常识别功率谱密度（PSD）的峰值或直接输出PSD矩阵的奇异值，但由于频域模态识别方法每次重新运算都需要初步校准，且对噪声非常敏感，因此，该类方法在桥梁健康监测中存在较大局限性。时域方法通常着重于稳定图的自动解析，以获取有代表性的模态，目前，大跨桥梁健康监测中使用最多的时域方法是随机子空间法（SSI）。然而，现阶段无论时域方法还是频域方法都面临3个技术难点需要克服：1）过滤虚假模态;2）准确区分和识别具有相近特征值的密集模态;3）实时、连续地自动识别模态参数，为实时有限元模型修正和快速损伤诊断提供可能。

Altunisik等[15]分别采用SSI算法与改进的FDD算法（EFDD）识别了一座木桥，通过对比研究发现：在未经信号降噪处理时，频域算法与时域算法的模态参数识别结果基本一致。黄珍等[16]以某大跨斜拉桥一年的实测数据为依托，对桥梁结构运营模态分析方法（OMA）中常用的频域方法和时域方法展开对比分析。该研究结果证明，SSI法识别的主梁和斜拉索模态参数，与频域方法识别结果区别不大;数据驱动随机子空间算法（Data-SSI）主梁参数识别精度较协方差随机子空间算法（Cov-SSI）略高;将EEMD降噪处理方法与Data-SSI算法相结合，能有效剔除虚假模态，具有较强的抗噪能力，识别的主梁模态参数优于Data-SSI识别结果。

大跨度斜拉桥和悬索桥等柔性桥梁通常表现出低频特性，且具有密集模态。采用OMA识别此类大跨柔性桥梁的模态参数时，常常在计算密集模态时产生“漏阶”现象，即只能识别到密集模态中能量较强的模态，而未识别到能量较低的模态。Zhu等[17]为了解决这个问题，提出了一种贝叶斯频域算法，并应用于江阴大桥的环境振动测试，识别效果良好，能过滤虚假模态，还能区分、识别密集模态。此外，Liu等[18]提出了一种结合方法来区分和识别密集模态，该方法结合了扩展解析模式分解方法（AMD）、递归希尔伯特变换（recursive HT）和变频同步压缩小波变换（ZSWT）3种算法。这种结合方法能够追踪环境激励下时变结构的瞬时特性，但此研究仅采用悬臂梁和缆索结构作为试验验证，还尚未应用到实际大跨柔性桥梁结构中，因此，算法是否鲁棒仍需进一步研究。

为了实现模态参数的自动化识别，同时为了剔除虚假模态并区分、识别具有相近特征值的密集模态，Mao等[19]提出了一种大跨桥梁模态参数自动识别的方法。该研究应用了主成分分析（PCA）、K-means均值聚类和分层聚类这几种机器学习方法来改进Data-SSI。与以往其他改进的SSI算法相比，该方法在识别模态参数前利用PCA先剔除模态验证准则向量（Modal validation criteria vector）中的噪声分量，从而达到提升识别精度与节省运算时间的效果。此外，Mao等[19]在该研究中还提出了一种确定聚类分析最优参数的算法，最终通过该方法实现了苏通大桥模态参数的连续自动识别，得到该桥的“时间模态频率”关系如图3所示。

陈永高等[20]认为桥梁结构真实模态存在一般规律，并利用试验对其进行验证;然后根据稳定图的基本原理和聚类方法提出以频率值、阻尼比和振型系数为筛选因子的真实模态智能筛选算法;最后以某大跨斜拉桥为研究对象进行模态参数识别，并依次将识别得到的频率值、阻尼比以及振型系数与動载试验结果对比，再和有限元分析结果对比，两组对比分析结果表明：该算法可以剔除虚假模态，也能实现大跨桥梁健康监测系统的模态参数自动化识别。

为了解决Cov-SSI在自动化识别模态参数时面临的人工干预、参数设定不统一等问题，贺敏等[21]提出了两阶段改进稳定图自动识别模态的方法：首先，将模态参数不确定度指标引入第一阶段虚假模态参数剔除过程，实现最大程度虚假模态参数剔除;然后，凭借改进的FCM聚类算法，采用迭代策略计算不同聚类数目的隶属度矩阵，构造累积邻接矩阵，并结合图切割算法解析累积邻接矩阵，最终自动确定最佳聚类数目，实现了该算法的自动识别。贺敏通过某大跨悬索桥的实测振动数据，验证了所提方法的可行性。

周筱航等[22]在桥梁振动台模型试验中对比了确定子空间算法（DSI）和确定随机子空间算法（CD-SSI）的模态参数识别效果，对比结果表明CD-SSI算法具有更好的稳定性。同年，周筱航等[23]为了跟踪识别多输入多输出桥梁结构的时变模态参数，又提出了一种结合滑窗技术与确定随机子空间识别的时域识别算法（SW-CD-SSI），通过试验证明了该算法比希尔伯特黄变换算法（HHT）具有更高的精度和稳定性，可精确地跟踪桥梁频率在时域上的变化情况;采用SW-CD-SSI算法识别运营中某大跨斜拉桥（图4）[14，23]，由此可见，该方法能识别到的模态频率数量十分可观，且随着运营时间变化仍呈现较强稳定性。同年，张二华等[14]在SW-CD-SSI算法的研究基础上提出了张量随机子空间算法，该方法在保证识别精度的同时还兼具更高的计算效率，能实现大跨斜拉桥模态参数的自动化识别。

与SSI、ERA、PP和FDD等传统运营模态分析方法（OMA）相比，盲源分离方法（BSS）作为一种兴新模态识别工具越来越受到人们的重视。然而，文献中采用BSS方法识别实际工程结构的例子很少。Xu等[24]将BSS方法中的稀疏成分分析算法（SCA）进行改进，然后将其应用到一座大跨斜拉桥的模态参数识别中，获得了良好的效果。Xu等的研究证明，这种改进的SCA算法比工程中常用的SSI算法更能区分和识别密集模态，且对人工干预和参数选择的依赖性很小，实用于桥梁健康监测;此外，与OMA不同，该算法仍然保持了BSS的优点：即不考虑激励力的性质，对车辆、风载等脉冲激励引起的非线性非平稳信号仍具备识别能力。

5 有限元模型修正研究

近年来，桥梁结构有限元模型修正通常是通过调整设计参数（密度和刚度）来实现的，调整参数的方法又分为灵敏度矩阵法（SA）[25-27]和响应面法（RSM）[26，29-31]，其中，响应面法具有更高的计算效率。替代模型技术引入了参数敏感性分析的统计性质，将试验设计、参数子结构、多元逐步回归、假设检验等计入到结构有限元模型计算中，此外，替代模型技术还能与SA和RSM有机结合。为了提高复杂桥梁结构有限元模型修正的计算效率，越来越多的学者采用Kriging预估器和响应面模型等替代模型方法[26，29-31]来逼近结构响应与修正参数之间的关系，以提升有限元模型修正的计算速率。

Ferrari等[25]提出了一种将拉丁超立方体采样（LHS）、灵敏度分析（SA）和全局优化算法相结合的有限元模型修正自动化实施策略，并将该方法应用于一座服役已过百年的钢筋混凝土拱桥监测中，通过对该拱桥前8阶自振模态实测值与修正后有限元模型理论值的MAC指标展开分析，验证了该方法的有效性。Castro等[26]采用多项式替代模型技术与全局灵敏度分析方法修正了一座服役多年的砖石拱桥的有限元模型，该研究将环境振动激励法与激光扫描技术、探地雷达技术相结合，具有较好的创新性。Bartilson等[27]将灵敏度分析法、聚类算法与贝叶斯正则化方法相结合，修正了一座简支桁架桥和一座大跨悬索桥的有限元模型;该研究证明，在有限元模型修正中，正则化方法可以用来比较不同修正参数的重要程度，但除了增加或减少参数数量之外，并没有其它贡献，因此还需进一步研究正则化算法对有限元模型修正的利用价值。

由于有限元模型中边界条件的正确模拟对于模型的准确性至关重要，Hester等[28]研究了小跨径公路桥梁支座性能的测试与识别方法，目的是为有限元模型修正中边界条件的参数化建模提供依据;Hester在该研究中首次提出将支座位移计入有限元模型修正中，以降低盲目修正各构件密度和刚度而得到错误收敛结果的风险。

现阶段，由于桥梁健康监测系统的兴起，考虑实测数据不确定性的有限元模型修正研究已经越来越多。Yin等[29]以实测模态为目标响应，提出了一种考虑不确定性的概率有限元模型修正方法，该方法同时确定隐神经元的合适数量、隐层与输出层间传递函数的具体形式，得到了一种高效的贝叶斯神经网络（BNN），用来替代计算效率低下的有限元模型;然后，将优化后的神经网络应用到某人行天桥的不确定性有限元模型修正中，取得了良好的效果。

目前，响应面法仍然是桥梁有限元模型修正中应用最为广泛的替代模型技术。为建立适用于钢管混凝土桥梁的高效、高精度有限元分析模型，马印平等[30]等提出一种全桥多尺度有限元模型修正的响应面方法，通过某座钢管混凝土组合桁梁桥的理论计算与实桥试验结果对比验证了该方法的可行性与可靠性。单德山等[31-32]为获得桥梁结构的基准状态，考虑测试和结构参数的不确定性，将区间分析、仿射算法引入响应面有限元模型修正方法中，建立了一种新的桥梁结构有限元不确定模型修正方法，并根据斜拉桥振动台模型桥在不同工况下的测试模态参数和斜拉索索力，对其进行了有限元模型的不确定修正，实现了实测响应与有限元计算响应间误差的最小化，验证了这种不确定性有限元模型修正方法的有效性和正确性。

目前，学者们[25-29]通常采用模态置信准则（MAC）作为评判修正后模型动力特性的关键指标。然而，MAC评判指标的可靠性过于依赖测点数量，即有限范围内所布置的传感器数量越多，MAC评判越可靠。因此，Ngan等[33]采用泽尼克矩指標（ZMD）作为模型修正后的模态相关性验证指标，通过对一座人行天桥的有限元模型修正证明：当布置的传感器数量有限时，对于结构局部范围内的模态相关性检验而言，ZMD指标比MAC指标更具优势。

6 损伤识别研究

学者们在2019年中的研究表明[14，19-23]，模态参数的实时自动化识别技术已经在桥梁健康监测系统中完全实现。然而，桥梁损伤识别仍未实现自动化快速分析，因此，损伤诊断技术还无法在桥梁健康监测系统中得到广泛应用。现阶段，桥梁损伤识别研究主要从时域信号（加速度时程等）中提取结构特征（模态参数、模态曲率等），然后通过模式识别和机器学习方法从中挖掘损伤信息，力图准确、快速地实现损伤定位和损伤程度诊断。

金梦茹[34]针对同时包含桥梁静态响应与动态响应的结构响应向量（SRV），将PCA降维方法与BP神经网络（BPNN）方法相结合，提出了关于大跨斜拉桥的损伤识别方法，并通过对珠江黄埔大桥的损伤诊断验证了该方法的可行性。

Sen等[35]提出了一种基于PCA的两阶段损伤诊断方法，该方法分为训练和测试两个阶段。在训练阶段，将来自健康结构系统的模态频率数据用来构造训练数据集的主成分方向;在测试阶段，将受损状态结构系统的实测数据投射到训练模型估计的主方向上，利用投影到主分量上数据的斜率，分离温度变化和结构损伤对实测数据的影响，展开进行有效的结构损伤诊断。最后，Sen通过对瑞士Z24桥的损伤识别证明了所提方法的鲁棒性。

为了在桥梁健康监测系统中实现快速损伤诊断，Cardoso等[36]针对环境随机激励引起的实测振动信号，提出了一种全自动实时无监督的损伤识别方法：该方法首先采用K-medods聚类算法对时程信号数据进行模式识别，得到结构损伤特征（NI）;再通过跟踪特征值NI，进行异常值分析，获取损伤指标（D）;最后，通过对一座高速公路桥梁进行快速损伤识别，验证了该方案的可行性。同年，Ngoc等[37]将ANN与布谷鸟搜索算法（CS）相结合，提出了一种针对大跨钢桁架桥梁的损伤识别方法，并顺利应用到某座系杆拱桥的损伤诊断中;该研究证明，将模式识别方法与全局搜索技术相结合，能够大幅提升损伤识别的计算精度和速率。

由于桥梁结构的损伤特征普遍存在于振动信号的高频部分，而斜拉桥、悬索桥等大跨柔性桥梁具有低频的密集模态，现阶段SSI等模态参数识别算法在区分低频的密集模态时仍显得不够成熟，因此，基于桥梁动力参数的传统损伤识别方法受到了严峻挑战;在此背景下，基于过桥车辆动力参数的桥梁损伤识别方法应运而生[38-40]。Mei等[38]首次提出通过将振动传感器安装在车辆上，利用机器学习方法中的MFCC算法（Mel-frequency cepstral coefficient）和PCA算法从过桥车辆的振动信号中提取与桥梁损伤相关的转换特征，最终识别得到桥梁结构的损伤位置和损伤程度。同年，Liu等[39]也利用过桥车辆的振动信号，提出了一套数据驱动的桥梁损伤诊断方案，该方案采用信号处理和模式识别技术实现了对桥梁结构损伤程度的高精度比较和估计。首先，该研究通过公式推导和有限元仿真分析证明，不同损伤程度下桥梁跨中位置的加速度幅值呈非线性变化，且车辆通过传感器测点时信号响应的高频段中包含大量损伤程度信息;然后，通过对AE的进行训练，开展桥梁损伤程度的比较与估计;最后，采用一座试验模型桥验证了该方案的有效性。

除了上述基于振动信号的桥梁损伤识别方法，2019年度还涌现出许多针对混凝土裂缝、钢材裂纹的损伤识别研究[41-47]，这些研究同样普遍采用模式识别、图像识别和机器学习等技术方法。

此外，张晓艳等[44]研究了桥面曲率和挠度对损伤识别的敏感程度：在实验室内对一座T型简支梁桥模型进行了多级加载，通过三维激光扫描系统采集了桥面三维点云数据，通过对不同损伤工况下的实验数据与有限元模拟数据进行对比分析，提出了基于桥面高斯曲率变化的损伤识别方法。该研究证明，桥面高斯曲率相对于挠度变化而言，对结构损伤更为敏感。李春良等[45]为了精确识别三跨变高度连续梁桥的损伤，根据傅里叶级数理论和数值积分法建立了变高度连续梁桥的整体刚度模型和中支座反力二次差值损伤模型，通过判定中支座反力二次差值曲线是否发生突变及其突变程度，提出了一种有效的损伤识别方法。简正坤等[46]为了提高桥梁结构的损伤识别准确率，并摆脱对桥梁损伤前信息的依赖，提出了基于应变指标和D-S证据理论的损伤识别方法，并通过实验验证了该方法的鲁棒性。

7 状态预测与评估研究

桥梁健康监测系统研究的最终目标是实现结构状态的快速预测与实时评估。然而，对于大跨复杂桥梁结构而言，影响其整体结构状态的因素众多，计算工作量大，现阶段尚未完全实现桥梁结构综合状态的快速预测与实时评估。

Zhou等[48]提出了一种健康状态综合测量系统（HSCMS），并结合多指标相关评价方法对公路桥梁进行健康监测与状态评估。该方法首先识别公路桥梁结构应力应变和断裂发展等力学行为，然后对桥梁结构强度、刚度和承载力进行评估，最后采用多指标相关评价方法对一座高速公路连续梁桥的长期使用性能进行预测评价，具有较强的参考价值和一定的指导作用。该方法虽引入了传感器信号识别分析机制，但仍十分依赖传统的静载试验方法;因此，该方法虽可以保证较高的桥梁状态评估精度，但仍未实现桥梁状态预测与评估的快速化、实时性。

Scozzese等[49]以意大利一座长期经受洪水冲刷的圬工拱桥为研究对象，通过OMA技术识别该桥的模态频率与振型，验证了有限元仿真模型的准确性，通过对该模型进行洪水冲刷模拟，发现拱桥模态特性对墩底土体侵蚀程度十分敏感，因此，提出了基于OMA的实时监测预警系统，从而对该桥进行实时预警与状态评估。该研究证明，基于动力特性的桥梁结构状态预测与评估方法值得进一步研究。

Mangalathu等[50]提出了一种基于机器学习的桥梁震害损伤快速诊断方法，该研究采用随机森林算法（RF）建立了损伤状态随桥梁结构参数变化的训练模型，并使用这种方法实现了对美国加州某连续梁桥的震后快速损伤评估。然而，该研究仅考虑了桥墩损伤，却忽略了桥梁其他构件的损伤，因此，这种震后桥梁损伤状态评估方法有待进一步研究。

王高新等[51]根据大胜关长江大桥支座的纵向动位移监测数据，利用动位移监测值的累加概率特性拟合得到广义极值分布函数，然后通过蒙特卡洛抽样模拟（MCS）得到设计使用寿命内的动位移累积行程，最后基于支座超过磨损上限的失效概率对该大跨铁路钢拱桥的支座磨损状态进行了安全状态评估。该方法不仅评估表明大胜关长江大桥所有球型钢支座尚未达到磨损上限，还预测了这些支座在整个设计使用寿命内的磨损状态，因此，具有重要的工程价值。

为了在桥梁伸缩缝失效前预警，Ni等[52]基于长期桥梁健康监测数据研究了桥梁伸缩缝状态评估和安全预警的贝叶斯方法：首先建立表征桥梁温度与伸缩缝位移之间的贝叶斯回归模型，依据可靠性理论制定了伸缩缝位移异常指标，最终实现了某大跨斜拉桥伸缩缝位移的安全预警与状态评估。

8 结论与展望

对桥梁健康监测中多项关键技术方法的研究现状进行了详细介绍，并对这些技术方法在2019年中的相关研究进展进行了总结和评述，以促进对桥梁健康监测有更全面深入的理解。桥梁健康监测作为桥梁工程领域一个新兴发展的研究分支，在中国已经发展了十几年，尤其是实测信号数据的降噪处理、模态参数识别等研究和应用已经发展得较为成熟，而与之相关的有限元模型修正和损伤识别等技术方法仍尚不成熟、完善，有待进一步研究。

2019年，各种聚类方法广泛应用于信号数据的降噪处理与模态参数识别研究中，最终在桥梁健康监测系统中实现了模态参数的自动化识别，取得了显著突破。越来越多的有限元模型修正研究开始考虑不确定性，也开始尝试使用贝叶斯神经网络等全新的替代模型方法，并取得了良好的效果。与此同时，桥梁损伤识别研究几乎全部采用模式识别技术与机器学习方法，并首次提出将振动传感器安装在过桥车辆上，通过间接测量实现桥梁结构的损伤诊断。综上所述，桥梁健康监测的各项关键技术已经离不开模式识别技術和机器学习方法的辅助，相关研究已经全面步入到多学科交叉结合的路线上来;尤其是ANN、CNN和BNN等各类神经网络方法，已在2019年度应用于传感器信号预处理、有限元模型修正和损伤识别等多项健康监测关键技术领域，并取得了显著的研究成果。

总体来说，桥梁健康监测的研究及应用仍处于起步阶段，信号数据的预处理、降噪处理和模态参数识别等研究仍需要进一步完善，有限元模型修正、损伤识别、结构状态预测与评估等重难点技术的研究工作仍面临许多困难需要克服，这也需要新一代桥梁工作者不懈努力，建立跨学科学习与合作机制，不断探索与创新。参考文献：

[1] 孙利民， 尚志强， 夏烨. 大数据背景下的桥梁结构健康监测研究现状与展望[J]. 中国公路学报， 2019， 32（11）： 1-20.

SUN L M， SHANG Z Q， XIA Y. Development and prospect of bridge structural health monitoring in the context of big data [J]. China Journal of Highway and Transport， 2019， 32（11）： 1-20. （in Chinese）

[2] GATTI M. Structural health monitoring of an operational bridge： A case study [J]. Engineering Structures， 2019， 195： 200-209.

[3] NEVES A C， LEANDER J， GONZLEZ I， et al. An approach to decision-making analysis for implementation of structural health monitoring in bridges [J]. Structural Control and Health Monitoring， 2019， 26（6）： e2352.

[4] 陈华， 张表志. 小河特大桥健康监测系统架构设计及实施建议[J]. 公路交通科技（应用技术版）， 2019， 15（2）： 172-175.

CHEN H， ZHANG B Z. Architecture design and implementation suggestions of health monitoring system for Xiahe Bridge[J]. Journd of Highway and Transportation Research and Development， 2019， 15（2）： 172-175.

[5] 顾津申. 石济客专济南黄河桥健康监测系统总体设计[J]. 铁道工程学报， 2019， 36（4）： 54-59.

GU J S. General design of health monitoring system for the Yellow River bridge of Shijiazhuang-Jinan passenger dedicated line [J]. Journal of Railway Engineering Society， 2019， 36（4）： 54-59.（in Chinese）

[6] FU Y G， PENG C， GOMEZ F， et al. Sensor fault management techniques for wireless smart sensor networks in structural health monitoring [J]. Structural Control and Health Monitoring， 2019， 26（7）： e2362.

[7] 向阳， 杜君. 桥梁健康监测系统中的大数据分析与研究[J]. 铁路计算机应用， 2020， 29（1）： 44-48， 54.

XIANG Y， DU J. Bridge health monitoring system based on big data technology [J]. Railway Computer Application， 2020， 29（1）： 44-48， 54. （in Chinese）

[8] NI F T， ZHANG J， NOORI M N. Deep learning for data anomaly detection and data compression of a long-span suspension bridge [J]. Computer-Aided Civil and Infrastructure Engineering， 2020， 35（7）685-700

[9] 严鹏. 桥梁健康监测采样信号EMD小波相关降噪研究[J]. 噪声与振动控制， 2019， 39（3）： 204-209.

YAN P. Study on EMD Wavelet correlation de-noising of bridge health monitoring sampling signals [J]. Noise and Vibration Control， 2019， 39（3）： 204-209.（in Chinese）

[10] 陈永高， 钟振宇. 基于改进EEMD算法的桥梁结构响应信号模态分解研究[J]. 振动与冲击， 2019， 38（10）： 23-30.

CHEN Y G， ZHONG Z Y. Modal decomposition of response signals for a bridge structure based on the improved EEMD [J]. Journal of Vibration and Shock， 2019， 38（10）： 23-30. （in Chinese）

[11] 劉欣悦， 单德山， 谭康熹. 基于互补集合经验模态分解的近场脉冲地震信号降噪算法[J]. 铁道建筑， 2019， 59（5）： 59-63.

LIU X Y， SHAN D S， TAN K X. Near-fault pulse-like earthquake signals denoising algorithm based on complementary ensemble empirical mode decomposition [J]. Railway Engineering， 2019， 59（5）： 59-63. （in Chinese）

[12] HUANG S X， WANG X P， LI C F， et al. Data decomposition method combining permutation entropy and spectral substitution with ensemble empirical mode decomposition [J]. Measurement， 2019， 139： 438-453.

[13] ZHANG E H， SHAN D S， LI Q. Nonlinear and non-stationary detection for measured dynamic signal from bridge structure based on adaptive decomposition and multiscale recurrence analysis [J]. Applied Sciences， 2019， 9（7）： 1302.

[14] 张二华. 桥梁结构时变系统的张量子空间识别研究[D]. 成都： 西南交通大学， 2019.

ZHANG E H. Research on tensor subspace identification of time-varying system for bridge structures [D]. Chengdu： Southwest Jiaotong University， 2019. （in Chinese）

[15] ALTUNISIK A C， KALKAN E， OKUR F Y， et al. Non-destructive modal parameter identification of historical timber bridges using ambient vibration tests after restoration [J]. Measurement， 2019， 146： 411-424.

[16] 黃珍， 单德山， 李乔. 大跨斜拉桥运营模态分析方法对比 [J]. 应用基础与工程科学学报， 2019， 27（1）： 144-155.

HUANG Z， SHAN D S， LI Q. Comparison of operational modal analysis methods for long span cable-stayed bridge [J]. Journal of Basic Science and Engineering， 2019， 27（1）： 144-155. （in Chinese）

[17] ZHU Y C， AU S K， BROWNJOHN J M W. Bayesian operational modal analysis with buried modes [J]. Mechanical Systems and Signal Processing， 2019， 121： 246-263.

[18] LIU J L， ZHENG J Y， WEI X J， et al. A combined method for instantaneous frequency identification in low frequency structures [J]. Engineering Structures， 2019， 194： 370-383.

[19] MAO J X， WANG H， FU Y G， et al. Automated modal identification using principal component and cluster analysis： Application to a long-span cable-stayed bridge [J]. Structural Control and Health Monitoring， 2019， 26（10）： e2430.

[20] 陈永高， 钟振宇. 桥梁结构真实模态的智能化识别[J]. 振动工程学报， 2019， 32（3）： 471-479.

CHEN Y G， ZHONG Z Y. Intelligent identification of the real mode for bridge structures [J]. Journal of Vibration Engineering， 2019， 32（3）： 471-479. （in Chinese）

[21] 贺敏， 梁鹏， 李琳国， 等. 基于两阶段改进的FCM法的模态参数自动识别[J]. 东南大学学报（自然科学版）， 2019， 49（5）： 940-948.

HE M， LIANG P， LI L G， et al. Automatic modal parameter identification based on improved two-stage FCM algorithm [J]. Journal of Southeast University （Natural Science Edition）， 2019， 49（5）： 940-948. （in Chinese）

[22] 周筱航， 单德山， 谭康熹， 等. 确定子空间识别方法在桥梁振动台模型试验中的对比[J]. 长安大学学报（自然科学版）， 2019， 39（4）： 73-81.

ZHOU X H， SHAN D S， TAN K X， et al. Comparison of deterministic subspace identification methods for model bridge shaking table test [J]. Journal of Changan University （Natural Science Edition）， 2019， 39（4）： 73-81.（in Chinese）

[23] 周筱航， 单德山， Inamullah Khan， 等. 多输入多输出桥梁结构时变模态参数的滑窗时域识别[J/OL]. 应用基础与工程科学学报. http：//kns.cnki.net/kcms/detail/11.3242.TB.20190304.1620.002.html

ZHOU X H， SHAN D S， KHAN I， et al. Sliding window time-domain method for identifying time-varying modal parameter of multi-input and multi-output bridge structure [J/OL]. Journal of Basic Science and Engineering， http：//kns.cnki.net/kcms/detail/11.3242.TB.20190304.1620.002.html.（in Chinese）

[24] XU Y， BROWNJOHN J M W， HESTER D. Enhanced sparse component analysis for operational modal identification of real-life bridge structures [J]. Mechanical Systems and Signal Processing， 2019， 116： 585-605.

[25] FERRARI R， FROIO D， RIZZI E， et al. Model updating of a historic concrete bridge by sensitivity- and global optimization-based Latin Hypercube Sampling [J]. Engineering Structures， 2019， 179： 139-160.

[26] BAUTISTA-DE CASTRO， SNCHEZ-APARICIO L J， CARRASCO-GARCA P， et al. A multidisciplinary approach to calibrating advanced numerical simulations of masonry arch bridges [J]. Mechanical Systems and Signal Processing， 2019， 129： 337-365.

[27] BARTILSON D T， JANG J， SMYTH A W. Finite element model updating using objective-consistent sensitivity-based parameter clustering and Bayesian regularization [J]. Mechanical Systems and Signal Processing， 2019， 114： 328-345.

[28] HESTER D， KOO K， XU Y， et al. Boundary condition focused finite element model updating for bridges [J]. Engineering Structures， 2019， 198： 109514.

[29] YIN T， ZHU H P. An efficient algorithm for architecture design of Bayesian neural network in structural model updating [J]. Computer-Aided Civil and Infrastructure Engineering， 2020， 35（4）354-372

[30] 馬印平， 刘永健， 刘江. 基于响应面法的钢管混凝土组合桁梁桥多尺度有限元模型修正[J]. 中国公路学报， 2019， 32（11）： 51-61.

MA Y P， LIU Y J， LIU J. Multi-scale finite element model updating of CFST composite truss bridge based on response surface method [J]. China Journal of Highway and Transport， 2019， 32（11）： 51-61. （in Chinese）

[31] 单德山， 顾晓宇， 李中辉， 等. 桥梁结构有限元模型的仿射-区间不确定修正[J]. 中国公路学报， 2019， 32（2）： 67-76.

SHAN D S， GU X Y， LI Z H， et al. Affine-interval uncertainty updating of finite element model for cable-stayed bridge [J]. China Journal of Highway and Transport， 2019， 32（2）： 67-76.（in Chinese）

[32] SHAN D S， CHAI Y H， ZHOU X H， et al. Tension identification of suspenders with supplemental dampers for through and half-through arch bridges under construction [J]. Journal of Structural Engineering， 2019， 145（3）： 04018265.

[33] NGAN J W， CAPRANI C C， BAI Y. Full-field finite element model updating using Zernike moment descriptors for structures exhibiting localized mode shapes [J]. Mechanical Systems and Signal Processing， 2019， 121： 373-388.

[34] 金梦茹. 基于结构响应向量与机器学习的损伤识别方法研究[D]. 广州： 华南理工大学， 2019.

JIN M R. Damage identification methods based on structural response vectors and machine learning algorithms [D]. Guangzhou： South China University of Technology， 2019. （in Chinese）

[35] SEN D， ERAZO K， ZHANG W， et al. On the effectiveness of principal component analysis for decoupling structural damage and environmental effects in bridge structures [J]. Journal of Sound and Vibration， 2019， 457： 280-298.

[36] DE ALMEIDA CARDOSO R， CURY A， BARBOSA F. Automated real-time damage detection strategy using raw dynamic measurements [J]. Engineering Structures， 2019， 196： 109364.

[37] TRAN-NGOC H， KHATIR S， DE ROECK G， et al. An efficient artificial neural network for damage detection in bridges and beam-like structures by improving training parameters using cuckoo search algorithm [J]. Engineering Structures， 2019， 199： 109637.

[38] MEI Q P， GL M， BOAY M. Indirect health monitoring of bridges using Mel-frequency cepstral coefficients and principal component analysis [J]. Mechanical Systems and Signal Processing， 2019， 119： 523-546.

[39] LIU J X， CHEN S H， BERGS M， et al. Diagnosis algorithms for indirect structural health monitoring of a bridge model via dimensionality reduction [J]. Mechanical Systems and Signal Processing， 2020， 136： 106454.

[40] LOCKE W， SYBRANDT J， REDMOND L， et al. Using drive-by health monitoring to detect bridge damage considering environmental and operational effects [J]. Journal of Sound and Vibration， 2020， 468： 115088.

[41] OSKOUI E A， TAYLOR T， ANSARI F. Method and monitoring approach for distributed detection of damage in multi-span continuous bridges [J]. Engineering Structures， 2019， 189： 385-395.

[42] RUBIO J J， KASHIWA T， LAITEERAPONG T， et al. Multi-class structural damage segmentation using fully convolutional networks [J]. Computers in Industry， 2019， 112： 103121.

[43] DUNG C V， SEKIYA H， HIRANO S， et al. A vision-based method for crack detection in gusset plate welded joints of steel bridges using deep convolutional neural networks [J]. Automation in Construction， 2019， 102： 217-229.

[44] 张晓艳， 汪富资， 于辉， 等. 基于面曲率变化的模型桥损伤识别方法研究[J]. 重庆交通大学学报（自然科学版）， 2019， 38（10）： 33-40.

ZHANG X Y， WANG F Z， YU H， et al. Damage detection method of bridge model based on curvature variation of bridge deck [J]. Journal of Chongqing Jiaotong University （Natural Science）， 2019， 38（10）： 33-40.（in Chinese）

[45] 李春良， 林志豪， 王方彦， 等. 三跨变高度连续梁桥的精确损伤识别[J]. 铁道学报， 2019， 41（12）： 96-105.

LI C L， LIN Z H， WANG F Y， et al. Accurate damage identification of three-span varying depth continuous girder bridge [J]. Journal of the China Railway Society， 2019， 41（12）： 96-105. （in Chinese）

[46] 簡正坤， 刘习军， 张素侠. 基于应变指标和D-S证据理论的简支梁桥损伤识别[J]. 实验力学， 2019， 34（5）： 791-799.

JIAN Z K， LIU X J， ZHANG S X. Damage identification in simply supported beam bridge based on strain index and D-S evidence theory [J]. Journal of Experimental Mechanics， 2019， 34（5）： 791-799.（in Chinese）

[47] WANG Y， TUMBEVA M D， THRALL A P， et al. Pressure-activated adhesive tape pattern for monitoring the structural condition of steel bridges via digital image correlation [J]. Structural Control and Health Monitoring， 2019， 26（8）： e2382.

[48] ZHOU C Y， WU Y T， CUI G J， et al. Comprehensive measurement techniques and multi-index correlative evaluation approach for structural health monitoring of highway bridges [J]. Measurement， 2020， 152： 107360.

[49] SCOZZESE F， RAGNI L， TUBALDI E， et al. Modal properties variation and collapse assessment of masonry arch bridges under scour action [J]. Engineering Structures， 2019， 199： 109665.

[50] MANGALATHU S， HWANG S H， CHOI E， et al. Rapid seismic damage evaluation of bridge portfolios using machine learning techniques [J]. Engineering Structures， 2019， 201： 109785.

[51] 王高新， 丁幼亮， 劉华， 等. 基于支座动位移监测的高铁桥梁支座磨损状态安全评估[J]. 中国铁道科学， 2019， 40（1）： 39-46.

WANG G X， DING Y L， LIU H， et al. Safety evaluation on wear condition of bearings for high speed railway bridge based on dynamic displacement monitoring [J]. China Railway Science， 2019， 40（1）： 39-46.（in Chinese）

[52] NI Y Q， WANG Y W， ZHANG C. A Bayesian approach for condition assessment and damage alarm of bridge expansion joints using long-term structural health monitoring data [J]. Engineering Structures， 2020， 212： 110520.

（编辑 胡玲）