基于自适应秩选方法的地震降秩去噪
杨志鹏, 陈秀清, 李 勇, 陈力鑫, 庞 谦, 马泽川, 王登伟
(1.四川省地震局 西昌地震中心站,四川 西昌 615022;2.成都理工大学 地球物理学院,成都 610059;3.四川省地震局 地震监测中心,成都 610041)
人工地震勘探是资源勘查、活断层探测、地质构造分析的重要手段[1-3]。勘探环境的复杂化和勘探深度的增加致使采集得到的地震数据中有效反射信号较弱,且往往被强随机噪声覆盖[4]。地震随机噪声一般具有分布频带宽、振动无规律、随机分布于整个地震道等特征,由地下复杂介质构造和其他不确定因素共同作用产生。地震随机噪声会对后续的诸如多次波衰减、地震波反演成像、地震道重建、地质构造分析等数据处理与解释流程产生严重影响[5-6],因此压制地震随机噪声是地震资料弱信号提取与增强的重要步骤。目前,主流的地震随机噪声压制方法可以分为5个大类[7-8]:基于域变换和滤波理论方法[9-10]、基于稀疏变换理论方法[11-13]、基于信号分解理论方法[14-16]、基于机器学习理论方法[17-18]、基于降秩理论方法[19-25]。
基于降秩理论的去噪方法主要是对地震数据构建特殊数学矩阵,再利用低秩逼近(秩约化)方法对其进行降秩处理,达到去除随机干扰的目的[26]。对频域地震数据构造Hankel矩阵是常见做法之一,并相继发展出利用截断奇异值分解(TSVD)方法[19]、阻尼奇异值分解(DSVD)方法[20]、阻尼最优异值收缩(DOptShrink)方法[24],低秩-稀疏混合约束(HRSC)方法[27]、结构低秩约束(HLR)方法[22]等秩约化方法对构造的Hankel矩阵进行降秩去噪,其中DSVD方法和DOptShrink方法还被拓展应用于五维地震资料的同步去噪与重建[21,28]。
基于Hankel矩阵的降秩去噪结果除了受秩约化方法限制外,另一关键因素为秩选参数,即纯净数据的秩值。尤其是在处理复杂构造的含噪地震资料及其分块计算时,由于纯净数据未知,秩约化方法的秩选参数难以准确测定,容易导致去噪不足或去噪过度问题[29]。为解决传统的固定秩选参数难以确定的问题,本文引入了一种基于奇异值最优硬阈值的自适应秩选方法[30-31],通过最优硬阈值系数和估计数据噪声水平计算出信噪分界奇异值大小,从而自适应地确定秩选参数。本文将其与TSVD方法、DSVD方法和DOptShrink方法相结合,提出自适应降秩去噪方法(ATSVD、ADSVD、ADOptShrink),利用理论模型和实际资料证明所提自适应降秩去噪方法从压噪性和保幅性上均较传统的基于固定秩选的去噪方法有所提高,且从计算效率等方面对新方法进行了探讨。
1 基于自适应秩选方法的地震数据去噪
1.1 Hankel矩阵降秩去噪
Hankel矩阵为沿反对角线元素相等的特殊数学矩阵,被广泛应用于矩阵降秩去噪、重建等领域。考虑时域三维地震数据可以表示为
Dtime(x,y,t)∈RNx×Ny×Nt
其中:Nx为Inline测线道数;Ny为Xline测线道数;Nt为时间轴采样点数。首先通过傅里叶变换将Dtime(x,y,t)由时域转换到频域
(1)
式中:Dfreq(x,y,ω)∈RNx×Ny×Nω表示频域数据;Nω为频率切片数。对于每个特定的频率切片Dfreq(jΔω)∈RNx×Ny(1≤j≤Nω)可以表示为矩阵
(2)
对该频率切片分量Dfreq(jΔω)中每行数据构造Hankel矩阵,如第i(1≤i≤Nx)行数据构建的Hankel矩阵可以表示为[30]
(3)
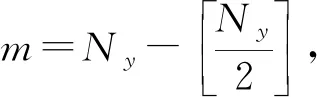
(4)
理论证明,对于由线性同相轴构成的无噪地震数据,其每个频率切片构造的块Hankel矩阵H具有低秩性质,且秩的大小等于剖面中不同倾角线性同相轴的个数[30,32-33],数据的缺失或随机噪声的存在都会显著增加矩阵H的秩值大小(图2)。因此通过对块Hankel矩阵H的进行秩约化处理,可以压制随机噪声,恢复有效信号[25]。
1.2 秩约化方法
1.2.1 TSVD方法
考虑观测矩阵H∈Ra×b由信号分量X∈Ra×b(rank(X) =r H=X+N (5) 通常,低秩矩阵去噪问题在最小二乘意义下的一般形式可以表示为 (6) (7) (8) (7)式为观测矩阵H的奇异值分解形式,xi为H的奇异值,ui和νi分别为H的左、右奇异向量。 1.2.2 DSVD方法 (9) (10) 式中:I为单位阵;k为控制Ti衰减程度的阻尼参数。 1.2.3 DOptShrink方法 为了克服直接使用核范数对秩函数进行凸松弛近似无法得到最优解的问题,R.R.Nadakuditi[34]提出利用观测矩阵低秩特性先验,通过TSVD逼近观测矩阵非凸秩函数的优化方法OptShrink,利用门限阈值对奇异值进行收缩处理。考虑建立非凸优化去噪问题,将(6)式转化为一般形式 (11) (12) (13) 式中:xi为H的第i(1≤i≤r)个奇异值;Σ为由奇异值序列xr+1,xr+2, …,xa-1,xa构成的对角阵;D(·)和D′(·)为互逆的特定变换算子,分别定义为 (14) (15) 利用(9)式的阻尼项进一步约束OptShrink,结果可得到DOptShrink方法降秩矩阵[24,28] (16) 为解决上述问题,本文在秩约化方法中引入了基于奇异值最优硬阈值的自适应秩参数选择方法[35-36]。该方法在渐近均方误差(asymptotic mean squared error, AMSE)框架下,利用大维随机矩阵理论和渐近矩阵理论设计奇异值最优硬阈值的选取,进而自适应地选取秩参数。假设Z∈Ra×b为标准正态分布的高斯白噪声,σ为噪声的标准差(噪声水平),则(5)式模型可以简化为 H=X+σZ (17) (18) 令β=a/b(0<β≤1),矩阵维数a和b趋于无穷大,而X的秩和非零奇异值固定,即 (19) 基于(18)式、(19)式的渐近模型,则此时奇异值硬阈值系数λ的AMSE框架可定义为 (20) (21) (22) (23) (24) 但当噪声水平σ未知条件下,在应用(24)式时还应首先对σ进行噪声水平估计 (25) 式中:xmed是观测矩阵H的奇异值序列的中值;μβ是β基于随机矩阵理论的Marcenko-Pastur分布定律的中值解,即求解 (26) 联立(23)式、(24)式、(25)式、(26)式可以得到在噪声水平σ未知情况下奇异值最优硬阈值τ*为 (27) 最后,通过判断奇异值xi是否大于最优硬阈值τ*来判断自适应秩选参数r*的大小 r*=#{i,xi≥τ*} (28) 综上分析,将自适应秩选方法分别与常规的TSVD、DSVD、DOptShrink等秩约化方法相结合,分别提出了自适应截断奇异值分解(ATSVD)、自适应阻尼奇异值分解(ADSVD)、自适应阻尼最优奇异值收缩(ADOptShrink)等自适应降秩去噪方法。 自适应降秩去噪方法的去噪流程如下: (1)首先将三维地震数据体Dtime(x,y,t)进行分块预处理,时空窗滑动,读取第i个时空窗内子数据块Dtime(x,y,t)i。 (2)利用傅里叶变换将Dtime(x,y,t)i从时域转换到频域Dfreq(x,y,ω)i,对其每个频率切片Dfreq(x,y,jΔω)i构造块Hankel矩阵H。 (5)时空窗继续滑动,读取第i+1个时空窗内子数据块Dtime(x,y,t)i+1,重复第(2)-第(4)步操作,直至分块子数据全部处理完毕。 为定量评估上述方法的去噪性能,本文采用信噪比(RSN)和局部相似属性(local similarity, LS)作为衡量去噪效果的标准[37-38]。 (29) 局部相似属性是基于随机噪声与有效信号局部正交的先验,可用于无参考场景的压噪效果评价及检测是否存在有效信号泄漏,其数值在区间[0, 1]变化,值越大的区域说明局部相似程度越高,有效信号的能量泄漏问题就越严重,即方法保幅能力越差[7,30,38]。同维矩阵A和B之间的局部相似属性LS定义为 (30) (31) (32) 其中:a=diag(A),b=diag(B),diag(·)为矩阵取主对角线上元素的算子。(30)式和(31)式中的最小平方目标函数优化问题可由带局部光滑约束的整形正则化方法求解 (33) (34) 其中λ是控制物理维度和收敛速度的参数,Γ为整形算子。 首先将本文的方法应用于雷克子波构建的三维线性模型[39](图7-A),该模型包含4条不同主频的线性同相轴,数据大小为300×40×40(时间采样点数×Inline道数×Xline道数),采样间隔为4 ms。在模拟信号基础上加入50%的高斯白噪声,使得该线性模型的信噪比为 -10.780 2 dB,得到含噪数据(图7-B),可以看出有效信号被强噪声所覆盖,同相轴细节变得十分模糊,很难识别出有效信号。由于该模型严格满足同相轴为线性的假设条件,因此可对该模型数据整体直接应用降秩去噪方法进行处理,选取固定秩选参数r为4,阻尼参数k为5。实验中,我们使用传统的基于固定秩选参数的降秩去噪方法TSVD、DSVD、DOptShrink和本文所提基于自适应秩选方法的降秩去噪方法ATSVD、ADSVD、ADOptShrink作为对比研究,结果如图7-C、E、G、D、F和H所示。从图7的各种方法纵向对比来看,基于本文改进方法的去噪结果背景更为干净,残余噪声更少;横向对比来看,DSVD和DOptshrink去噪结果明显优于TSVD的去噪结果,ADSVD和ADOptShrink去噪结果也优于ATSVD。 表1给出了6种方法处理后的信噪比,也可以看出本文改进方法相较于原方法在信噪比上均有所提高,其中ADSVD方法和ADOptShrink方法信噪比分别提高到 13.211 5 dB和 13.304 9 dB。从图8各种方法的局部相似属性剖面可以看出,全局均接近于零值,指示各种方法在处理由线性同相轴构成的地震数据时,均具有较好的保幅性。 表1 三维线性模型各种方法去噪前后的信噪比Table 1 Signal to noise ratio (SNR) of de-noising results by various methods of 3D linear model 图9为模拟信号在加入不同强度高斯白噪声后,各种方法去噪后的信噪比,可以看到DOptShrink方法、ADSVD方法、ADOptShrink方法去噪后的信噪比最高,且十分接近。图10为各种方法在不同秩选参数下,对图7-B含噪数据处理后的信噪比。可以看出传统降秩去噪方法需在秩选参数r严格取为同相轴的倾角数时,才能取得最高信噪比;此后随着r的增大,更多的噪声成分会被引入去噪结果,导致信噪比下降。但相对而言DOptShrink方法下降趋势更缓,因为该方法对秩选参数并不敏感[28],而本文方法结果则完全不受固定值r影响。图11为在ubuntu环境下利用Matlab2016b计算平台,配置为Intel Core i5-8400CPU@2.80 GHz、4GB RAM时,统计的各种方法在不同秩选参数下的运算时间。由于降秩去噪方法的时间复杂度集中在奇异值分解步骤上,因此引入自适应秩选方法并不会显著增加运算时间。另一方面,可以看到DOptShrink方法结果虽然对秩选参数r不敏感,但其运算时间会随r的增大而显著增加,因此为获得较好的去噪效果而对其选择一个较大的秩值并不理想。 为了测试本文的方法,在处理由非线性同相轴构成的地震数据时的去噪表现,引入一个合成的三维双曲模型[40](图12-A)。该三维合成数据中包含5个不同曲率的双曲线同相轴,数据大小为128×101×101,同样在模拟信号基础上加入50%高斯白噪声,得到含噪数据(图12-B),由于噪音的加入,有效波的同相轴能量被严重干扰,只剩下大致轮廓可见。为了满足线性同相轴假设,提高处理效果,将该模型分割为50×50×50的计算子窗口。由于受秩非一致性问题影响,对各个不同的处理子窗口,只能经验性地选取统一的固定秩选参数r为15,阻尼参数k为5。各种方法处理结果如图12-C、D、E、D、F、G和H所示。从图中可见TSVD方法去噪结果仍存在有大量的残余噪声,去噪效果最差;而DSVD方法和OptShrink方法的去噪结果虽然较好地去除了背景噪声,但受计算窗口内不当的秩选参数影响,同相轴在曲部发生了扭曲和断裂,且信号边缘存在伪影现象。而本文所提的ATSVD、ADSVD、ADOptShrink这3种方法去噪结果的同相轴连续、清晰,且背景无明显噪点。这是由于新方法可以通过自适应秩选方法调整秩值大小,在每个计算子窗口内数据驱动地获得理想秩值,因此可以得到优化后的去噪结果。从图13所示的各种方法局部相似剖面也可以看到传统的基于固定秩选的降秩去噪方法在局部有明显的信号泄漏现象,相对的基于自适应秩选方法的降秩去噪方法则具有较好的保幅性能。 观察该双曲模型在不同强度噪声下各种方法去噪后的信噪比(图14)、各种方法在不同秩选参数下对含噪50%的双曲模型处理后的信噪比(图15),以及各种方法在不同秩选参数下对该模型的运算时间(图16),可以看出基于自适应秩选方法的降秩去噪结果去噪性能相对较好,且不受秩选参数取值影响,也不会显著增加时间复杂度,尤其是对于DOptShrink方法,结合自适应秩选方法后,还会显著提高运算效率。 为验证本文方法的实际处理效果,将本文的方法应用于某工区陆上三维叠后实际地震记录[41](图17-A),该数据大小为300×200×200,时间采样间隔4 ms, 从图中可见随机噪声分布较多,同相轴模糊、错断、不连续,不利于构造解释工作。将该实际数据分割为50×50×50的计算子窗口,选取固定秩选参数r为15,阻尼参数k为5进行处理。为更清晰地展示资料处理前后的地震反射差异细节,抽取Inline为10的单道剖面进行对比(图17-B)。 图18为传统的基于固定秩选方法的去噪结果及其噪声差剖面,可以看到传统方法在箭头所指区域丢失了大量有效波信号,且同相轴边缘信息被处理得过于平滑,断层构造被涂抹。图19为基于自适应秩选方法的降秩去噪结果及其噪声差剖面,图中可见去噪结果视觉表现较好,不仅充分压制了随机噪声,使得整个剖面同相轴细节、连续性、断裂构造走向表现清晰;从噪声差剖面和图20所示局部相似属性剖面对比来看,有效信号也得到了充分保留,没有明显的同相轴损伤和丢失现象。 本文引入了一种基于奇异值最优硬阈值的自适应秩选方法替换秩约化方法中固定秩选参数,通过计算最优硬阈值系数和估计数据噪声水平得出潜在有效信号的秩值,从而克服了传统的基于固定秩值的降秩去噪方法在实际应用中的秩非一致性问题,最大限度地衰减随机噪声和保留有效信号。三维理论模型和实际数据试验证明,与传统的固定秩值降秩去噪方法相比,本文方法去噪后的信噪比相对更高,信号保持能力也相对最好,在计算效率上也有一定提升,因此建议将ADSVD方法和ADOptShrink方法推广应用于五维地震资料的自适应同步去噪与插值处理中。 浙江大学地球科学学院陈阳康研究员提供了数据并进行了讨论,作者借此表达感谢。
1.3 自适应秩选方法
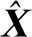
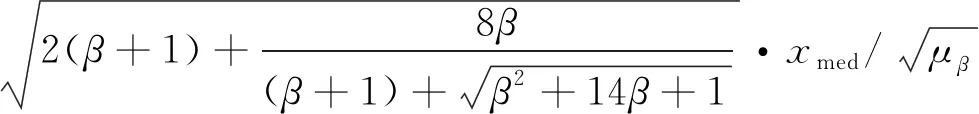
1.4 自适应降秩去噪方法
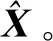
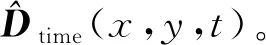
2 模型与算例
2.1 线性模型测试

2.2 双曲模型测试
2.3 实际资料测试
3 结论和建议

