火灾后中空夹层高强钢管高强混凝土抗弯性能
刘 晓, 徐翰文, 卢孟超
(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)
中空夹层钢管混凝土结构(concrete filled doubled skin steel tube,CFDST)相对传统的钢管混凝土结构(concrete filled steel tube,CFST)而言,具有更高的承载能力、延性和抗火性能[1-6].因此中空夹层钢管混凝土广泛应用于高层建筑、大跨径桥梁等现代建筑中.随着我国技术的发展与科技的进步,高强度的材料逐渐应用在建筑结构之中.一般把抗压强度超过60 MPa的混凝土称为高强混凝土,把屈服强度超过460 MPa的钢材称为高强钢材.中空夹层高强钢管高强混凝土结合了高强材料质量轻、强度高的优点,在保证强度的同时极大地减轻自重.
目前国内外学者对常温下的中空夹层钢管混凝土和高强钢管混凝土构件的力学性能进行了大量研究.陈培超等[7]对高温后圆钢管约束型钢混凝土短柱进行了有限元分析.赵磊等[8]对火灾后方钢管再生混凝土的轴压进行了有限元分析,得出构件的极限承载力随着再生骨料取代率的增加而逐渐降低. Liew等[9]对高强钢管混凝土梁柱结构的力学性能进行了研究.Portolés等[10]对高强钢管混凝土的偏压性能进行了试验研究.张哲等[11]对高强钢管混凝土的耐火性能进行了研究.对于钢-混凝土组合结构的研究,王晓初等[12]通过理论推导的方法比较并修正了不同国家FRP筋混凝土梁抗弯承载力的计算公式.周乐等[13]对FPR钢结构的受压承载力和屈曲载荷进行研究,并根据试验曲线推导出对应的公式.
纯弯是构件仅受弯矩作用,无轴向载荷作用下的特殊情况,虽然这种受力情况在实际工程中比较少见,但是研究CFDST的纯弯受力状态对继续研究其偏压和压弯的情况具有重要意义,有必要对此类构件抗弯性能进行研究.目前对火灾后中空夹层高强钢管高强混凝土纯弯构件力学性能的研究还未见报道.因此本文采用ABAQUS软件,建立火灾后中空夹层高强钢管高强混凝土梁纯弯力学性能的有限元模型,并验证模型的有效性.随后进行工程应用范围的参数分析,对火灾后中空夹层高强钢管高强混凝土梁在ISO-834的弯矩- 跨中挠度曲线进行评估.
1 有限元模型
1.1 材料本构关系
火灾后夹心混凝土的应力-应变关系模型采用林晓康[14]提出的火灾后混凝土应力-应变关系模型,该模型在考虑约束效应的混凝土应力-应变关系模型的基础上修正了峰值应力与峰值应变.火灾后高强钢材的应力-应变关系模型采用韩林海[15]提出的双折线模型,该模型即考虑了高强钢材的强化阶段,又考虑了经历高温后高强钢材屈服强度的衰减.在温度场的计算中,钢材和混凝土均采用文献[16]提出的热工参数.
1.2 模型的建立
火灾后模型采用顺序热-力耦合的方法建立,首先进行热力学分析,得出构件各节点的温度变化情况,再与常温的力学模型进行耦合,即模拟火灾后各节点受力情况.
为了组成中空夹层高强钢管高强混凝土梁,各个部件要被赋予不同的属性.在温度场中,设立夹心混凝土和盖板时,采用八结点线性传热六面体单元(DC3D8),内外钢管采用四结点传热四边形壳单元(DS4);模拟分析时,为保证壳体精度,在单元厚度方向选择9个积分点.为了保证钢管与夹心混凝土充分传热,采用Tie的接触方式.在力场中,夹心混凝土和盖板采用八结点线性六面体单元减缩积分, 沙漏控制(C3D8R);内外钢管采用四结点曲面薄壳或厚壳减缩积分, 沙漏控制, 有限膜应变(SR4).相互作用方面,混凝土和盖板采用表面与表面接触的方式连接,刚性大的作为主面,刚性小的作为从面,即内外钢管和盖板作为主面,夹心混凝土作为从面,盖板和钢管采用壳-实体耦合的接触方式.为更好地传递受力情况,混凝土与盖板之间的法线方向的接触采用“硬”接触.在实际试验中,钢管和混凝土会由于种种因素产生相对滑移,为了准确模拟这种情况,在切线方向采用“罚”函数的摩擦公式,摩擦系数取0.6.内外钢管和夹心混凝土采用边布种结构技术划分网格,两端盖板采用全局布种划分网格.为保证热-力耦合计算能够顺利进行,温度场和力场的网格划分一致.
模型采用位移加载的方式,即在梁靠近左右盖板的2个4分点处施加载荷.左右端分别限制X、Y、Z和X、Y方向的位移.构件的计算长度L均为1 400 mm,盖板采用240 mm×240 mm×20 mm的刚性板,各部件网格划分及构件加载方式如图1所示.
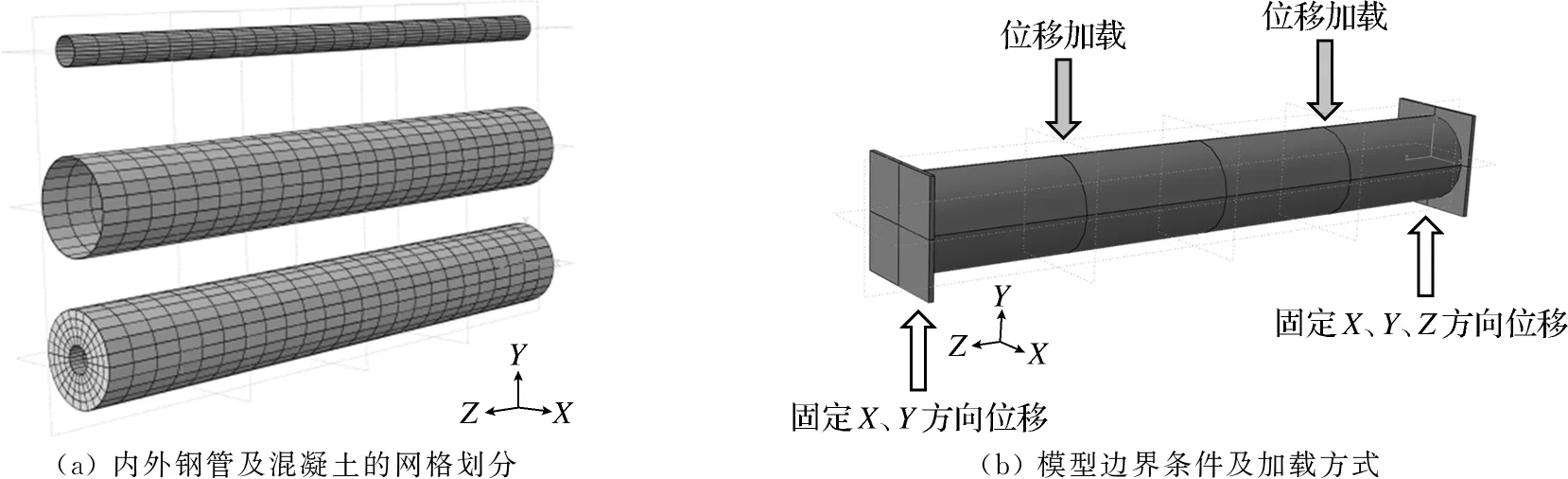
(a) 内外钢管及混凝土的网格划分(b) 模型边界条件及加载方式
1.3 模型验证
为验证所选本构关系及模型建立方法的正确性及合理性,结合文献[17]中受火时间为90 min的火灾后圆钢管混凝土cw-2,文献[18]中的常温下高强钢管高强混凝土和文献[19]中所经历温度为300 ℃的中空夹层方钢管高强混凝土bsc-1a、bsc-1b和所经历温度为500 ℃的中空夹层方钢管高强混凝土bsc-2a进行模拟验证.以上构件验证结果如表1所示,其中Di为内钢管的外径,Do(B)为外钢管的外径或边长,ti、to为内外钢管的壁厚,fyi、fyo为内、外钢管屈服强度,fcu为夹心混凝土抗压强度.由表可知,模拟值与试验值之比的平均值为1.031,方差为0.070,因此可认为所建立的有限元模型是合理可靠的.

表1 各文献中验证构件的具体参数Table 1 Specific parameters of verified specimens in various documents
2 参数分析
采用ABAQUS软件分析了受火时间t(60~180 min)、空心率χ(0.31~0.72)、混凝土抗压强度fcu(80~120 MPa)和内外钢管屈服强度fyi、fyo(345~690 MPa)对火灾后中空夹层高强钢管高强混凝土受弯承载力的影响.其中χ=Di/(Do-2to).建立了11组模型,对圆套圆的中空夹层高强钢管高强混凝土梁在火灾后的力学性能进行模拟,所有构件的模型参数见表2.抗弯承载力取外钢管受拉区纤维应变达到10 000×10-6时所对应的弯矩.

表2 模型参数Table 2 Parameters of models
第4和第5位上的数字3、4、5、6分别代表构件外钢管和内钢管采用345、460、590、690 MPa的钢材.
2.1 温度场分布情况
图2为不同空心率的构件在受火时间分别为60、90、120和180 min时的跨中截面温度分布情况,从图2可以看出温度以同心圆的方式分布,从外钢管到内钢管的方向,温度逐渐降低.空心率为0.31的构件内外温差最大,空心率为0.72的构件内外温差最小,这是因为空心率越小,构件所含的混凝土就越多,夹心的混凝土由于热惰性使得热量传递到内钢管的速度大为滞后,所以温差就越大.

(a) χ=0.31, t=60min(b) χ=0.31, t=90min(c) χ=0.31, t=120min(d) χ=0.31, t=180min(e) χ=0.52, t=60min(f) χ=0.52, t=90min(g) χ=0.52, t=120min(h) χ=0.52, t=180min(i) χ=0.72, t=60min(j) χ=0.72, t=90min(k) χ=0.72, t=120min(l) χ=0.72, t=180min
2.2 受火时间t
图3为空心率为0.52的构件C-10-5-4-4在经历不同受火时间下的弯矩(M)-跨中挠度(um)曲线.从图3可以看出,随着受火时间的增加,构件的抗弯承载力呈下降趋势,抗弯刚度随受火时间的增加略有减小.在达到最大抗弯承载力后,曲线随着受火时间的增加而趋于平缓,在构件跨中挠度达到L/40处(约35 mm)仍未出现下降段,表明中空夹层高强钢管高强混凝土在火灾后仍表现出较好的后期延性.受火时间从60~90 min时,构件的抗弯承载力下降幅度最大,约为14%,这是因为混凝土在受火60 min后承载力下降,产生大量温度裂缝并且不可逆,由原来的内外钢管夹层混凝土共同承担弯矩转换为主要由内外钢管承担弯矩,而钢材的物理特性使其在火灾后恢复大部分的力学性能,使得构件在后期有较好的延性.因此曲线没有明显的下降段,较为平顺.综上可以看出,中空夹层高强钢管高强混凝土具有很好的耐火性和火后延性.

图3 不同受火时间对C-10-5-4-4构件抗弯承载力的影响
2.3 空心率χ
图4为不同空心率的构件C-8-3-4-4、C-8-5-4-4、C-8-7-4-4在受火时间为180 min时的弯矩-跨中挠度曲线.从图4可以看出,空心率为0.72的构件抗弯刚度比其他空心率构件的抗弯刚度大,延性也相比其他空心率构件的延性好.图5为最大纵向应变达到10 000×10-6时各个空心率对构件跨中截面中性轴的影响情况.从图5可以看出,所有构件的中性轴都靠近受压区一侧,这是因为混凝土相比钢材抗拉能力较弱.空心率为0.72的构件,其截面含钢率较大,参与受弯作用的钢材也多.故空心率为0.72的构件抗弯承载力最高,其次为空心率为0.52、0.31的构件.

图4 不同空心率对构件抗弯承载力的影响(t=180 min)
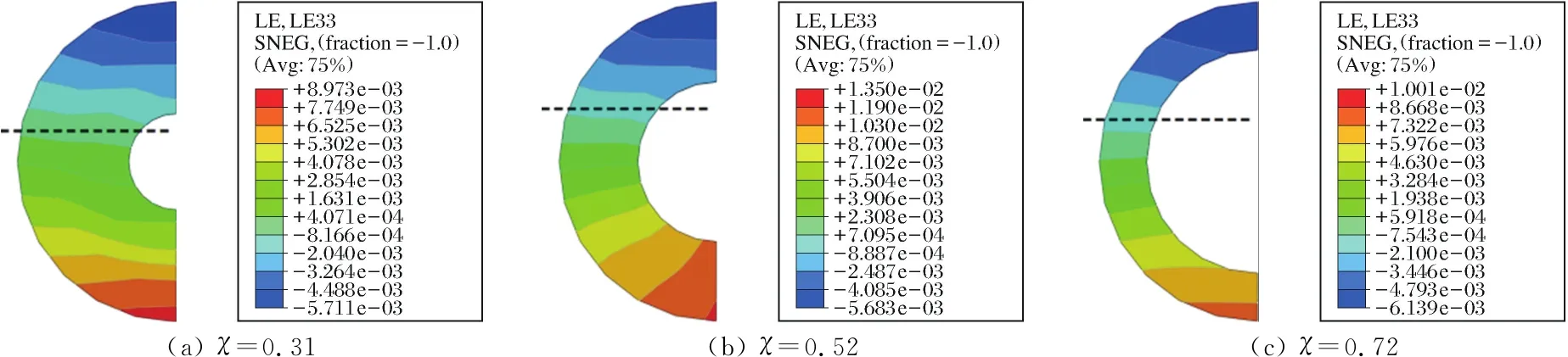
(a) χ=0.31(b) χ=0.52(c) χ=0.72
2.4 混凝土抗压强度fcu
图6为采用不同混凝土抗压强度的构件C-8-5-4-4、C-10-5-4-4、C-12-5-4-4在受火时间为90 min的弯矩-跨中挠度曲线.从图6可以看出,由于混凝土高温的热惰性,在受热后其承载能力恢复较差,混凝土抗压强度的变化对承载力和延性影响不大.
2.5 外钢管屈服强度fyo和内钢管屈服强度fyi
图7为受火时间为60 min的构件C-8-5-3-4、C-8-5-4-4、C-8-5-5-4、C-8-5-6-4在只有外钢管屈服强度不同时的弯矩-跨中挠度曲线.由图7可见,在其余条件相同的情况下,由普通钢到高强钢,构件的抗弯刚度影响不大,而抗弯能力提升明显,外钢管的屈服强度对整体承载力的提升最为明显,外钢管由Q345变为Q460时,构件的抗弯承载力从59.71 kN·m提升到71.71 kN·m,提升了20.1%,因此提高外钢管屈服强度对抗弯承载力影响显著.
图8为受火时间为60 min的构件C-8-5-4-3、C-8-5-4-4、C-8-5-4-5、C-8-5-4-6在只有内钢管屈服强度不同时的弯矩-跨中挠度曲线.由图可知,提升内钢管的屈服强度对提高构件的抗弯刚度影响不大,抗弯性能也略有增加.因此提升内钢管屈服强度对构件抗弯能力和延性没有明显作用.
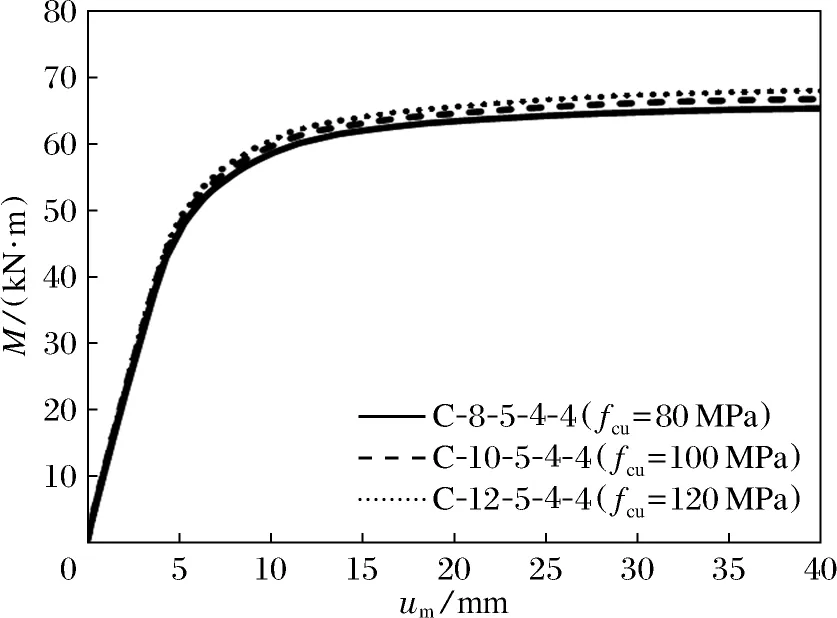
图6 混凝土抗压强度对构件抗弯承载力的影响(t=90 min)Fig.6 Influence of concrete compressive strength on ultimate bearing moment of specimens(t=90 min)

图7 外钢管屈服强度对构件抗弯承载力的影响(t=60 min)Fig.7 Effect of yield strength of outer steel tube on ultimate bending moment of specimens(t=60 min)

图8 内钢管屈服强度对构件抗弯承载力 的影响(t=60 min)
3 典型曲线分析
以C-8-5-4-4构件受火时间180 min为典型算例,分析中空夹层高强钢管高强混凝土纯弯构件的受力机理.典型构件的计算条件为Do=200 mm,Di=100 mm,to=ti=3 mm,fyo=fyi=460 MPa,fcu=80 MPa,χ=0.52,L=1 400 mm.图9为弯矩-拉压应变曲线,虚线为外钢管的屈服应变,由εyo=fyo/Eso得出,其中Eso为外钢管的弹性模量.由图9可以看出,受拉区的外钢管相比受压区先达到屈服极限.
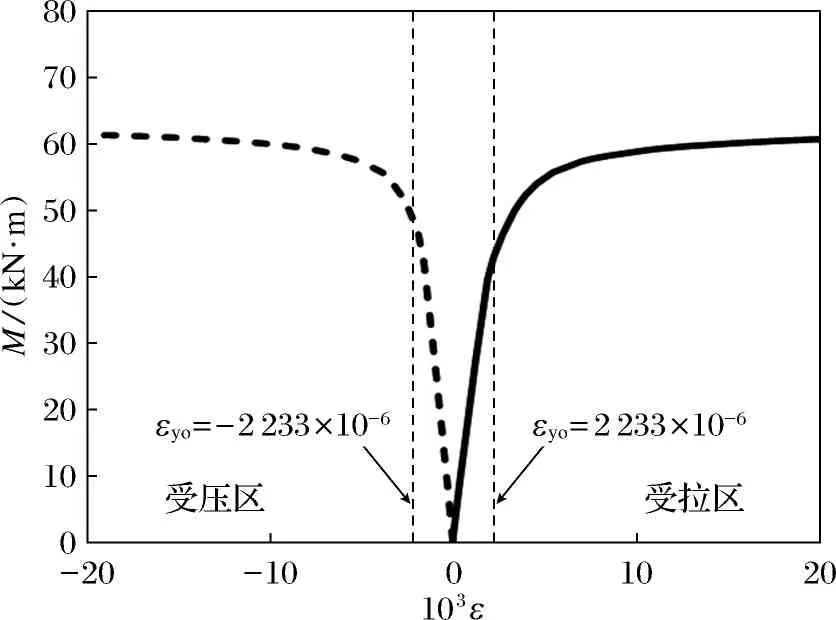
图9 弯矩-拉压应变曲线Fig.9 Moment-strain(tension and compression) curve
图10为火灾后中空夹层高强钢管高强混凝土构件及各组成部件承担弯矩情况.为方便描述,分别选取A、B、C三个参考点.由图10可见全过程曲线分为3个阶段.
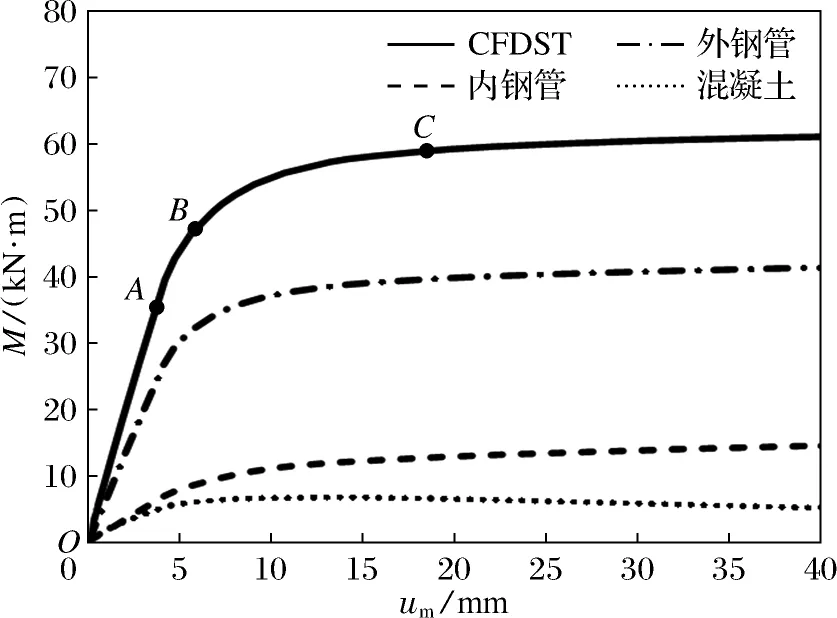
图10 整个构件及各组成部件承担弯矩情况
从O点到A点为弹性阶段,MA=0.6Mce,此时构件的弯矩-挠度关系基本为线性关系,这一阶段内外钢管与混凝土相互作用力较小,中性轴几乎和中心点的水平线重合,此阶段外钢管承担了近50%的弯矩.
从A点到C点为弹塑性阶段,此时随着载荷的增加,受压区外钢管逐渐达到屈服应变,导致承担的弯矩略有下降,由51.96%下降到50.89%,内钢管承担弯矩增加,由17.37%提高到21.05%.外钢管开始对核心混凝土产生约束效应,并在B点处左右达到峰值,随后逐渐下降,MB=0.8Mce.由于高温的作用,混凝土的力学性能并没有得到大量恢复,其所提供的抗弯能力也小于内钢管,弯矩相比挠度增加缓慢且呈非线性关系.
C点后为塑性阶段,MC=Mce.外钢管承载力提高到55.58%,且其趋势随构件的全过程曲线基本保持一致.内钢管提供的弯矩轻微增长,而混凝土提供的弯矩逐渐下降.整个构件在达到极限抗弯承载力后仍保持较好的延性,各部件在火灾作用后协同工作良好,表明中空夹层高强钢管高强混凝土纯弯构件具有较好的抗火性能.
4 结 论
1) 用ABAQUS软件计算得到了火灾后中空夹层高强钢管高强混凝土纯弯构件的弯矩-跨中挠度曲线,并且与已有试验结果吻合较好.
2) 火灾后中空夹层高强钢管高强混凝土构件的抗弯性能随受火时间的增加而减弱,提高外钢管的屈服强度对其抗弯性能提升显著.提高混凝土的抗压强度和内钢管的屈服强度对构件抗弯性能的提升作用不大.
3) 典型弯矩-跨中挠度全过程曲线分为弹性阶段、弹塑性阶段和塑性阶段.中空夹层高强钢管高强混凝土纯弯构件在经历火灾作用后,夹心混凝土由于热惰性丧失大部分力学性能,抗弯能力大幅度降低.内钢管受到混凝土的保护,力学性能恢复较好.构件整体的抗弯能力主要由内外钢管提供,抗火性能较好,经历火灾作用后仍具有较好的延性.

