关注图形变换的性质

熊诚燕

[摘要]新课标要求学生用图形变换的思维去研究三角形、平行四边形、圆等图形的性质.图形变换内容的加入，体现了动态几何的价值.分析探讨轴对称、平移、旋转的相关典例，使学生深刻理解图形变换的性质，提高学生解决图形变换问题的能力.

[关键词]图形变换;性质;轴对称

[中图分类号]G633.6

[文献标识码] A

[文章编号] 1674-6058（ 2020）35-0031-02

新课标要求学生用图形变换的思維去研究三角形、平行四边形、圆等图形的性质，图形变换内容的加入，体现了动态几何的价值，图形变换的性质是考试的重点和难点，当图形变换与其他特殊图形结合时，同时也考查了特殊图形的性质与判定.

一、轴对称的性质

成轴对称的两个图形，相对应的角其角度相同，相对应的线段其长度相等，这是轴对称最基本的性质，其他的性质还包括对称点的连线形成的线段，对称轴是其垂直平分线;对应线段或其延长线相交，交点一定在对称轴上;对应线段与对称轴的夹角彼此相等，把轴对称图形放在坐标系内，关于x轴对称的两个点的坐标，戈坐标相同，y坐标互为相反数;关于y轴对称的两个点的坐标，x坐标互为相反数，y坐标相同.

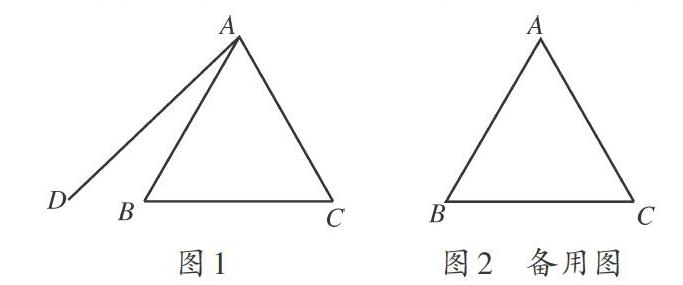
[例1]在等边△ABC外作射线AD，使得AD和AC在直线AB的两侧，∠BAD= a（0°

（1）依题意补全图1;

（2）在图1中，求∠BPC的度数;

（3）直接写出使得△PBC是等腰三角形的a的值，分析：（1）按作轴对称图形的步骤作图如图3所示.

（2）由轴对称性质，得AP=AB，根据圆周角定理解决问题，即点B关于直线AD的对称点为P，所以AP= AB，所以∠PAD=∠BAD，因为△ABC是等边三角形，所以∠BAC= 60°，AB= AC，所以AP =AB =AC，所以P，B，C在以A为圆心、AP为半径的圆上，所以∠BPC=1/2∠BAC= 30°;

（3）根据等腰三角形的性质分四种情形画出图形分别求解，即

①如图4-1中，当BP= BC时，a=∠BAD=30°;②如图4-2中，当PB= PC时，a=∠BAD= 75°;③如图4-3中，当CP= BC时，a=∠BAD=120°;④如图4-4中，当BP= PC时，a=∠BAD=165°，

综上所述，a的值为30°，75°，120°，165°，

评注：当几个点到一定点的距离相等时，则这几个点一定在同一个圆上，从而可以利用圆的性质解决问题.本题利用了圆周角定理，即同一条弧所对圆周角是它所对的圆心角的1/2以一条线段为边构造等腰三角形，一般有三种情况，要分类讨论避免漏解，

二、平移的性质

平移是图形的直线运动，平移后的图形与平移前的图形是全等形，即完全重合，所以相对应的角彼此相等，相对应的边彼此相等，对应边的位置关系是平行或在同一直线上，对应点的连线也互相平行或在同一直线上，图形中各部分所处的方位，在平移后所处的方位也不变，把平移前后的两个图形放在坐标系里，如果沿x轴左右平移，点的y坐标不变，x坐标左减右加;如果沿y轴上下平移，点的x坐标不变，y坐标上加下减.

[例2]在△ABC中，AD平分∠BAC交BC于点D.

（1）在图5中，将△ABD沿BC的方向平移，使点D移至点C的位置，得到△A'B'D'，且A'B'交AC于点E，猜想∠B'EC与∠A'之间的关系，并说明理由;

（2）在图6中，将△ABD沿AC的方向平移，使A'B'经过点D，得到△A'B'D'，求证：A'D'平分∠B'A'C.

三、旋转的性质

图形绕一固定点按某一方向转动一定的角度，这样的图形运动就是旋转，它是图形的圆周运动，旋转后的图形与旋转前的图形放在一起能完全重合，所以相对应的角其角度相同，相对应的线段其长度也相等，对应点连线后所成的线段，作它的中垂线一定经过旋转中心，两条这样的中垂线相交时，其交点就是旋转中心，旋转的角度可以用对应点与旋转中心连线的夹角得到，也是用对应线段的夹角得到.

[例3]如图7，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C= 90°.

（1）操作发现：如图8，若∠B= ∠DEC= 30°，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB上时，那么：①线段DE与AC的位置关系是什么？②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是什么？

（2）猜想论证：当△DEC绕点C旋转到图9所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，请你证明小明的猜想;

（3）拓展探究：如图10，若BC=3，AC=2，当△DEC绕点C旋转的过程中，四边形ABDE的面积是否存在最大值？若存在，请求出来;若不存在，请说明理由，

解析：（1）①DE//AC.理由如下：因为△DEC绕点C旋转，点D恰好落在AB边上，所以AC与CD相等，因为∠BAC= 90°- ∠B= 60°，所以△ACD是等边三角形，所以∠CD为60°，又因为∠CDE= ∠BAC= 60°，于是∠ACD= ∠CDE，所以DE//AC;

②根据含30。角直角三角形的性质，得CD=AC=1/2AB，于是BD=AD=AC，根据等边三角形的性质及三角形面积公式，得△ACD的边上的高AC=AD，根据等底等高的三角形的面积相等，得S△BDC=S△AEC，即S1=S2;

（2）如图11，作BC、CE的垂线，垂足分别为M、N，因为△DEC是由△ABC绕点C旋转得到，所以BC=CE.AC=CD，根据同角的余角相等，得∠ACN= ∠DCM，在△ACN和

评注：绕图形中的一个顶点旋转是旋转变换常考的类型，因为对应线段相等，所以此时常会形成等腰三角形，证明两个三角形面积相等的方法有：（1）两个三角形全等;（2）等底等高、同底等高、等底同高的两个三角形;（3）等量与等量的和相等;（4）等量与等量的差相等，

图形变换的性质还包括图形相似的性质，其中最重要的性质是两个相似图形的面积之比，与对应线段比的平方相等，在中考数学的选择题或填空题里常会单独考本部分知识，在解答题里常会与其他几何知识综合在一起考查，教师在教学时要注重问题情境的创设，联系生活实际，引导学生动手操作，让学生深刻理解图形变换的性质，同时渗透审美教育，在美的教育中激发学生的数学学习兴趣.

（责任编辑陈 昕）