阿波罗尼斯圆的逆向探究及其应用
佛山市南海区黄岐高级中学(528248) 熊向前
我们知道,到两个定点的距离之和、之差为定值的点的轨迹分别为椭圆、双曲线,那么到两个定点的距离之比为定值的点的轨迹是什么呢? 很多文章对此进行了研究,并得出了阿波罗尼斯圆的相关结论.本文在阿波罗尼斯圆的基础上进行逆向探究,得出了几个结论,并结合各地的高考题及模拟题给出相关应用.现整理成文,不当之处敬请批评指正.
一、问题的提出
题目(人教A 版必修二第124 页B 组第2 题)已知点M与两个定点O(0,0),A(3,0)的距离之比为求M的轨迹方程.(答案是(x+1)2+y2=4.)
该题反映了到两个定点的距离之比等于定值的点的轨迹问题,联想到椭圆、双曲线的定义,我们不禁会问: 平面内到两个定点的距离之比为常数的点的轨迹是否都是圆呢? 古希腊数学家阿波罗尼斯(公元前约262-190年)对这个问题进行了研究,并得出了阿波罗尼斯圆的相关结论.
阿波罗尼斯圆的定义: 设A、B是平面内两个定点,平面内动点P到A点与到B点的距离之比为常数λ(λ >0 且λ /=1),则点P的轨迹为圆,这个圆被称为阿波罗尼斯圆,简称阿氏圆,这两个定点我们称之为阿波罗尼斯圆对应的定点.

图1
证明如图1 所示,以直线AB为x轴,线段AB的中垂线为y轴建立直角坐标系,设AB=2a(a >0),则A(−a,0),B(a,0),设点P(x,y),则由定义得=λ,即所以P点的轨迹为以为圆心,以为半径的圆.
通过上述证明可以发现阿波罗尼斯圆有以下几个性质:
(1)阿波罗尼斯圆上任意一点到两个定点的距离之比为常数;
(3)阿波罗尼斯圆对应的两个定点与圆心在同一条直线上,且一个定点在圆内,一个定点在圆外.当λ >1 时,圆心在线段AB的延长线上,A点在圆外,B点在圆内; 当0<λ <1 时,圆心在线段AB的反向延长线上,B点在圆外,A点在圆内.
由阿波罗尼斯圆的定义可知,由两个定点及常数λ可确定一个圆,那么,对上述问题进行逆向思考,是否又有相关的结论呢? 笔者对此进行了探究.
二、阿波罗尼斯圆的逆向探究
探究一已知一个半径为r的圆O及常数λ(λ >0 且λ /=1),是否存在两点A、B,使得对圆上任意一点P都有=λ呢?A、B两点有何位置关系?
分析假设存在满足条件的两点A、B,以圆心O为原点,OA所在直线为x轴建立平面直角坐标系.则圆O的方程为x2+y2=r2,设A(m,0),B(n,s),设P(x0,y0)是圆O上任意一点,则有

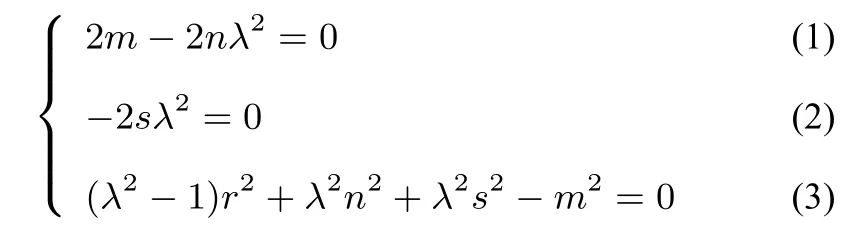
由(1)(2)得


联立(4)(5)得m=λr,n=所以存在两个定点使得对圆上任意一点P都有=λ,由这两点的坐标可知,它们都在过圆心O的一条射线上,且一个在圆内,一个在圆外.
忽略坐标系,我们可以得到以下结论:
定理1已知半径为r的圆O及常数λ(λ >0 且λ/=1),在过圆心O的任意一条射线上必存在唯一两定点A、B,使得对圆上任意一点P都有=λ,其中A、B两点满足OA=λr,OB=
探究二已知一个半径为r的圆O及圆内(或圆外)任意一定点A,在圆外(或圆内)是否存在一点B,使得等于常数呢? 此常数为多少?
由阿波罗尼斯圆的性质知,两定点与圆心三点共线,而由探究一的分析知,在阿波罗尼斯圆中,两定点A、B到圆心的距离满足OA·OB=r2,所以若存在满足条件的点B,则B必在射线OA上且OB=下面证明当A点在圆内时这样的点B满足条件.

图2
证明因为OB=所以当A点在圆内时,B点在圆外.如图2 所示,设P为圆O上任意一点,当P点不在直线OA上时,连接PO、PA、PB,因为OB=所以
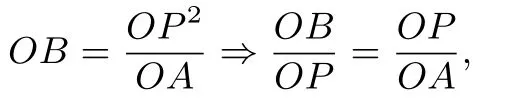
又由∠POA=∠BOP得ΔPOA∽ΔBOP,所以

当P点在线段AB上时,
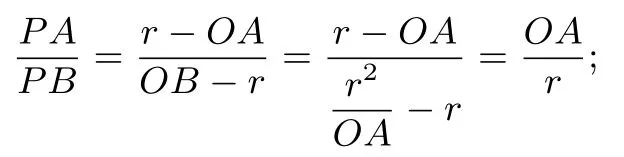
当P点在AB的反向延长线上时,
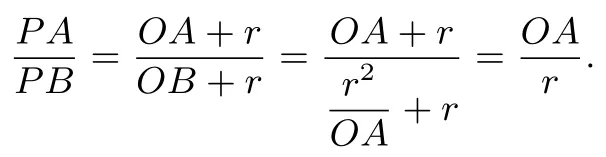
所以,对圆O上任意一点P都有等于常数,此常数为
同理可证,当A点在圆外时,线段OA上必存在一定点B且OB=使得对圆O上任意一点P都有为常数,且此常数等于由此我们可以得出以下结论:
定理2已知半径为r的圆O及圆O内(圆O外)一定点A,在OA的延长线(线段OA)上必存在一定点B且OB=使得对圆O上任意一点P都有为常数,此常数等于
联想到圆中极点与极线理论的知识,容易发现B点可看成是A点关于圆O对应的极线与直线OA的交点,因此B点也可以由以下几何方法作图得到: 若A点在圆内,则连接OA,过A点作OA的垂线交圆O于M、N两点,再过分别过M、N两点作圆O的切线,两切线的交点即为B点;若A点在圆外,则过A点作圆的切线得到两个切点,两切点的连线与直线OA的交点即为B点.
通过探究二的分析容易得到以下判定定理:
定理3对于半径为r的圆O及两定点A、B,若A、B两点在以圆心O为端点的射线上,且满足OA·OB=r2,则圆O为以A、B为定点的阿波罗尼斯圆,即: 对圆上任意一点P都有为常数,且此常数等于(证明过程同定理2 的证明基本一样,此处不再赘述)
三、阿波罗尼斯圆的应用举例
例1(2008年高考江苏卷)若AB=2,AC=则SΔABC的最大值是_____.
简析因为AC=所以从而C点的轨迹是以A、B为定点且比值λ=的阿波罗尼斯圆,此圆圆心在AB的延长线上,设其半径为r,则r=×2=所以SΔABC的最大值是
评析此题常规方法是以BC为变量,结合余弦定理及同角三角函数的平方关系或直接利用海伦公式将SΔABC表示成变量BC的函数,再转化成函数的最值问题,但运算量大,不易得出正确的答案,而结合阿波罗尼斯圆的概念,数形结合地去解决则大大减小了计算量,省时高效,形象直观,凸显问题的本质.
例2(2012年全国高中联赛福建预赛)已知圆C:(x −2)2+(y −2)2=m,点A(4,6),B(s,t);(1)略;(2)若s、t为正整数,且圆C上任意一点到A的距离与到B的距离之比为定值λ(λ >1),求m的值.
简析(2)由题意可知圆C可以看成是以A、B为定点以λ为比值对应的阿波罗尼斯圆,由阿波罗尼斯圆的性质可知,A、B两点及圆心C(2,2)三点共线,由于λ >1,故A在圆外,B在圆内,圆心C在线段AB的延长线上,所以有又因为s、t为正整数,解得s=3,t=4,从而得m=r2=CA·CB=10.
例3(2014年高考湖北文科卷)已知圆O:x2+y2=1和点A(−2,0),若点B(b,0)(b /=−2)和常数λ满足: 对圆O上任意一点M,都有|MB|=λ|MA|,则(1)b=____;(2)λ=____.
简析由题意可得圆O是以A、B为定点,以λ为比值对应的阿波罗尼斯圆,由阿波罗尼斯圆的性质可知:OA · OB=r2,所以OB=
评析例2、例3 用常规的解析方法不易得出正确答案,而利用阿波罗尼斯圆的相关性质去思考则可以将问题迅速“秒杀”.
例4已知点P在边长为2 的等边ΔABC的内切圆上运动,则AP+2PB的最小值是_______.
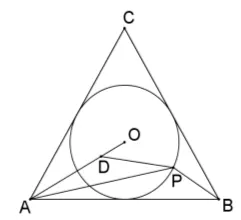
图3
分析该题最容易想到的方法是解析法,即建立平面直角坐标系,求出内切圆的方程,通过圆的参数方程形式将所求目标式表示成角度的函数,再通过导数知识求出最小值.这样做思路简单,但计算非常繁琐.
如图3 所示,由于P点是圆上一动点,A、B为圆外的两定点,故可考虑将圆O看成是点A或点B对应的阿波罗尼斯圆,因此可将AP或PB进行转化,结合目标式AP+2PB中的系数2 可知,应将圆O看成是点A对应的阿波罗尼斯圆.
由阿波罗尼斯圆的性质可知,在OA上存在一点D使得为定值,此时,所以PA=2PD,则AP+2PB=2PD+2PB=2(PD+PB),由图像可知,当P、B、D三点共线时,PD+PB最小,故

例5(2019年苏北七市三模)在平面四边形ABCD中,∠BAD=900,AB=2,AD=1.若=的最小值是____.
解析以A为原点建立如图4 所示的坐标系,则A(0,0),B(2,0),D(0,1),设C(x,y),则由可得C点的轨迹方程为(x −1)2+y2=4,故C点在以E(1,0)为圆心,2 为半径的圆上运动,根据所求目标式,考虑将圆E看成是点B对应的阿氏圆,则在EB的延长线上存在一点F,使得为定值,此时,所以CB=则故所求最小值为
评注例4、例5 可以归结为: 已知圆外或圆内的两个定点及圆上一动点,求a+λb的最小值问题,根据以上结论,实质上是已知阿波罗尼斯圆及对应的一个定点,要确定另外一个定点的问题,λ的值实际上是阿波罗尼斯圆中对应的比例常数.解决此类题目的方法是利用阿波罗尼斯圆的性质将a+λb转化成圆上动点与圆内外两定点的距离之和,再利用两点之间线段最短的几何性质来解决.

图4

图5
例6(2015年高考湖北理科卷)如图5,圆C与x轴相切与点T(1,0),与y轴正半轴交于点A,B(B在A的上方),且|AB|=2.(1)求圆C的标准方程; (2)过A作一条直线与圆O:x2+y2=1 相交于M,N两点,下列三个结论:其中正确的序号的____.(写出所有正确结论的序号)
解析(1)圆C的标准方程为(x −1)2+=2;(2)易求A(0,√−1),B(0,+1),因为圆C与x轴相切,由切割定理可得OT2=OA·OB,即OA·OB=r2(r为圆O的半径),故由本文定理3 可知,圆O为A、B两定点对应的阿波罗尼斯圆,由阿波罗尼斯圆的性质可得
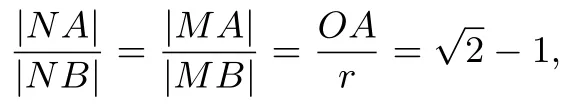
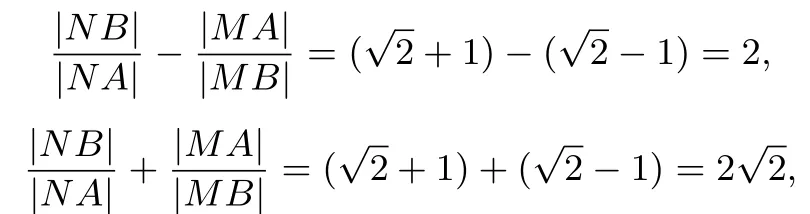
所以①②③均正确.
评注本题的命题背景实质上是阿波罗尼斯圆的相关性质,它将阿波罗尼斯圆藏得比较深,需利用圆中的切割定理来找到OA、OB与圆O半径的关系,进而发现圆O实际上是A、B两定点对应的阿波罗尼斯圆.相对于官方提供的解析法,本文的方法起到了四两拨千斤的效果.
四、结束语
许多高考试题都是课本例题、习题的变形、深化或拓展,体现了“高考题源于课本而又高于课本”的特点,因此,我们要重视引导学生对课本例题、习题的探究与推广,鼓励他们深入挖掘其内涵,这样不仅能理解问题的本质,还能帮助他们找到解决问题的通性通法,形成自己的“秒杀技巧”,提高探究问题的能力.

