基于电磁追踪系统的点云配准方法研究

孟晓亮， 张立晔， 房 超

(山东理工大学 计算机科学与技术学院，山东 淄博 255049)

1 引 言

近年来，随着计算机视觉技术的快速发展，结构光三维测量技术也被广泛应用于制造业、医学、机器视觉等领域。对于一个完整的物体，需要从不同视角进行多次测量，然后把它们拼合成一个整体才能反映物体表面的完整信息，这个过程称为点云配准[1]，也称为点云拼接。

点云配准按照其配准精度可以分为粗配准(也称初始配准)和精配准。目前，精配准方法中应用最为广泛的是Besl等人[2]提出的迭代最近点(ICP)算法及其改进算法[3-4]，该算法通过迭代最近点作为匹配点，计算获得使点对距离偏差最小的刚性变换，其配准效果的好坏依赖于粗配准的准确度，因此需要先对点云进行粗配准。现有的粗配准方法包括：(1) 基于点云自身特征的配准。孟禹等人[5]提出一种基于采样球的点云粗配准方法，通过寻找重叠区域内近似重合的3个点集，实现点云的粗配准；陆军等人[6]采用法向量和曲率加权计算、特征点提取、对应关系筛选方法，提高了配准的准确度和速度；伍梦琦等人[7]利用点云的几何特征和图像特征完成了点云的粗配准。此类方法针对点云特征明显的物体可以实现很好的配准，但针对特征较少和重叠区域较小的物体，其配准效果会受影响。(2) 基于辅助特征的配准。刘晓利等的[8]借助粘贴在被测物体表面的标志点求取坐标系转换矩阵，但该方法不适用于软质物体与易损物体的测量。孙军华等人[9-10]使用方格特征的平面靶标，利用方格角点的匹配求取坐标系转换矩阵。魏新国等人[11]采用圆形特征的平面靶标作为中介，求解前后测量位置的坐标系转换矩阵。此类方法不影响被测物表面自身的特征，但其测量范围受限，灵活性较低。(3) 基于机械定位的配准。徐永安等人[12]借助旋转的转台以实现点云的自动配准，在系统标定准确的情况下，能够得到较好的拼接准确度。但是此类方法的测量范围受限于机械结构的尺寸，系统灵活性较低，且工业现场测量时不便于携带。

综上所述，目前的点云粗配准方法都有一定的局限性。为此，本文提出一种基于电磁追踪系统的点云粗配准方法，利用电磁追踪系统高准确度的位移和姿态角信息，通过不同坐标系间的快速转换，实现点云的快速粗配准，再使用ICP精配准方法，实现点云的准确配准。最后，通过配准实验验证所提方法可有效提高粗配准的速度，并为ICP精配准提供良好的初值。

2 测量及配准系统组成

本文配准过程中使用的被测物点云信息由结构光三维测量系统获得。测量系统由一个工业相机及镜头、一个数字投影机和一台计算机组成，配准系统借助电磁追踪系统的发射器和接收器获取准确的位移和姿态角信息，如图1所示。

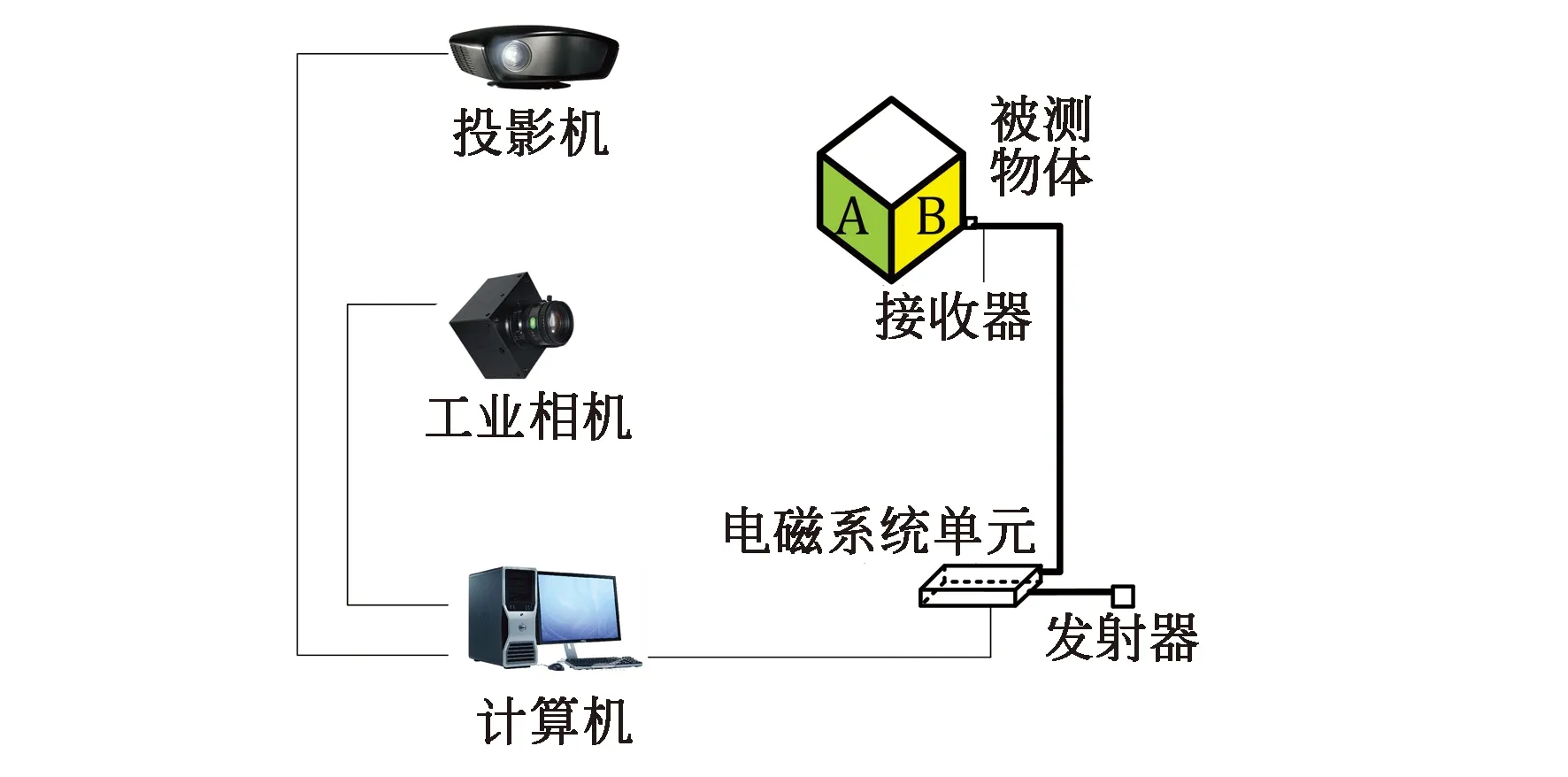
图1 测量及配准系统示意图

电磁追踪系统(FASTRAK)是美国Polhemus公司的一款电磁定位产品，由于其具有设备搭建简单、定位准确度高、速度快等特点，能实时返回准确的位移和姿态角信息。本文将借助该系统实现点云的粗配准。电磁追踪系统主要由电磁系统单元、发射器和接收器等组成。

电磁追踪系统的发射器发射电磁波，接收器通过传感器接收电磁波，依据电磁系统单元计算发射器和接收器之间准确的位移和姿态角信息，通过USB传输，就可以连接计算机得到接收器相对于发射器的位移(x,y,z)和姿态角(γ,φ,ω)6个参数的数据。其中，x、y、z分别为接收器相对于发射器X轴、Y轴和Z轴的位移。γ为绕发射器Z轴旋转的角度，φ为绕发射器Y轴旋转的角度，ω为绕发射器X轴旋转的角度。电磁追踪系统的位移准确度为0.076 mm，姿态角准确度为0.015°。

3 配准原理

本文采用结构光三维测量系统获取点云，并通过平移、旋转被测物体获取不同视角下的点云信息。将接收器与被测物体绑定，则接收器与被测物体之间的运动为刚体运动，通过接收器与发射器之间准确的位移和姿态角信息，发射器坐标系作为中间坐标系，将不同视角下获得的点云由世界坐标系转换到发射器坐标系下，再由发射器坐标系转换到接收器坐标系下，即实现了点云的粗配准。本文以两视角下的点云配准为例，阐述其配准原理。

3.1 基于平面的坐标系转换方法

采用结构光三维测量系统获取的点云都是相对于测量系统标定时的世界坐标系而言。不同的空间坐标系测量同一个平面时，将获得不同的平面方程，而被测量的平面唯一存在。可通过获取空间某一平面上的点云分别在世界坐标系和发射器坐标系中的拟合平面求解坐标系之间的转换关系。

首先，获取空间平面在世界坐标系和发射器坐标系下的平面方程。世界坐标系下，采用结构光三维测量系统，获得平面的点云坐标，利用最小二乘法拟合得到世界坐标系下的平面方程：

awxw+bwyw+cwzw+dw=0

.

(1)

发射器坐标系下，让接收器在空间平面上滑动，利用电磁追踪系统软件记录接收器中心点坐标序列，同样采用最小二乘法拟合出平面方程。由于接收器有一定的尺寸，接收器在测量平面上滑动时，得到的接收器中心点坐标序列所在平面与结构光测量系统拟合得到的平面平行，通过沿法线方向补偿一个深度值即可将两平面重合，并得到发射器坐标系下的平面方程：

atxt+btyt+ctzt+dt=0

.

(2)

其次，在平面上选取3组不共线的3个点，设在世界坐标系下3点分别为W1、W2、W3，在发射器坐标系下的3点分别为T1、T2、T3。在选取这3组对应点时，令xw=xt，yw=yt，zw和zt的值可根据式(1)和式(2)得到，令

，

(3)

，

(4)

令

ki=Ti-CW

，

(5)

，

(6)

式中，i=1, 2, 3，问题转化为求取如下目标函数：

.

(7)

根据奇异值分解(SVD)理论，有

.

(8)

可得

H=UΛVT

.

(9)

进而可以得到旋转矩阵RWT和平移向量TWT：

RWT=VUT

，

(10)

TWT=CT-RWTCW

.

(11)

求出RWT和TWT后，利用如下公式，将测得的点云由世界坐标系转换到发射器坐标系下：

，

(12)

式中，[xT,yT,zT]T为发射器坐标系下的点云，[xW,yW,zW]T为结构光三维测量系统获取的点云。

3.2 发射器坐标系与接收器坐标系转换关系的求取

配准过程中，发射器坐标系作为中间坐标系，因此还需要将点云由发射器坐标系转换到接收器坐标系下，其转换公式如下：

，

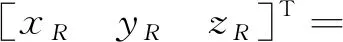
(13)

，

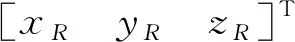
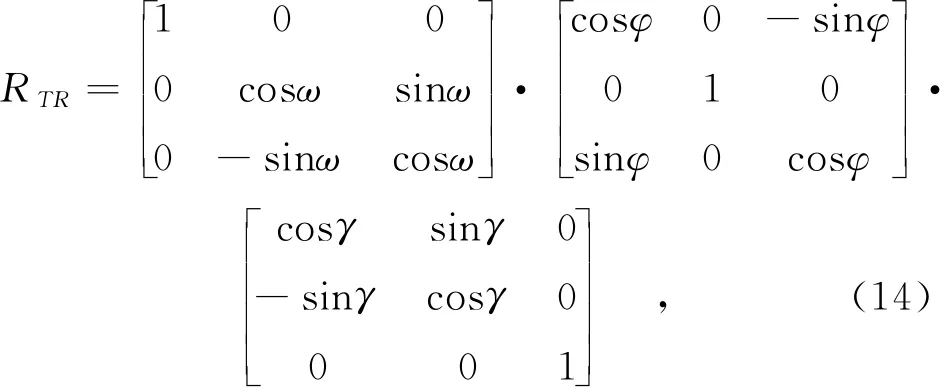
(15)

式中，(x,y,z)和(γ,φ,ω)可借助电磁追踪系统软件实时获取。

3.3 粗配准步骤

(1) 根据3.1节中描述的方法，求取发射器坐标系与世界坐标系的转换关系。

(2) 将接收器与被测物体绑定，形成刚性连接。并将被测物体放在结构光三维测量系统下进行测量，获取该视角下的点云信息，并记为(xA,yA,zA)，如图1所示，记录下此时接收器相对于发射器坐标系的位移和姿态角(x1,y1,z1,γ1,φ1,ω1)。

(3) 对被测物体旋转一定角度，获取旋转后该视角下的点云信息，并记为(xB,yB,zB)，记录下此时接收器相对于发射器坐标系的位移和姿态角(x2,y2,z2,γ2,φ2,ω2)。

(4) 将两视角下的点云根据3.1节中的方法由世界坐标系转换到发射器坐标系下，再根据3.2节中的方法由发射器坐标系转换到接收器坐标系下，合并两点云数据，即实现了点云的粗配准。

3.4 ICP精配准

ICP算法即迭代最近点算法，给定两视角下具有部分重叠的点云MA和MB以及它们之间的初始旋转矩阵R0和平移矩阵T0。假设在初始位置，点云MA中任意一点MAi和离点云MB中的最近一点MBi为一对匹配点，针对MA中的所有点查找其在MB中的最近点，然后求取最佳的R和T，使目标误差函数最小。接着更新点云的相对位置，重复以上过程，不断迭代，直至目标误差函数收敛或达到设定值，这就是ICP精配准算法的计算过程。目标误差函数的表达式如下：

，

(16)

式中，N为匹配点对的个数。

通过本文提出的粗配准方法，可实现两视角下被测物体的快速粗配准，为ICP精配准提供良好的初值。结合ICP精配准方法，可实现不同视角下点云的准确配准。

4 配准实验

本文采用一个大恒工业相机(型号为DH-HV3151UC，分辨率为2 048×1 536)和一个数字投影机(型号为Infocus 82，分辨率为1 024×768)搭建结构光三维测量系统，并固定好电磁追踪系统，通过结构光三维测量方法[13]获取单视角下被测物体的点云信息，系统各部分位置如图2所示。

图2 配准系统组成

4.1 平面配准实验

为评价本文所提方法的配准误差，针对不同深度(距离投影机的远近)位置的平面进行有重叠的两视角平移配准实验，通过计算配准后重叠区域点云最近点距离的平均值来评价配准误差，并采用ICP方法进行精配准，配准误差结果如表1所示。

由表1可以看出，粗配准后平面的配准误差在0.40 mm以下，经ICP精配准后，配准误差在0.04 mm 以下，所提粗配准方法能为ICP精配准提供良好的初值，验证了所提方法的有效性，且所提方法可对被测物体进行任意旋转或平移，配准过程更加灵活。

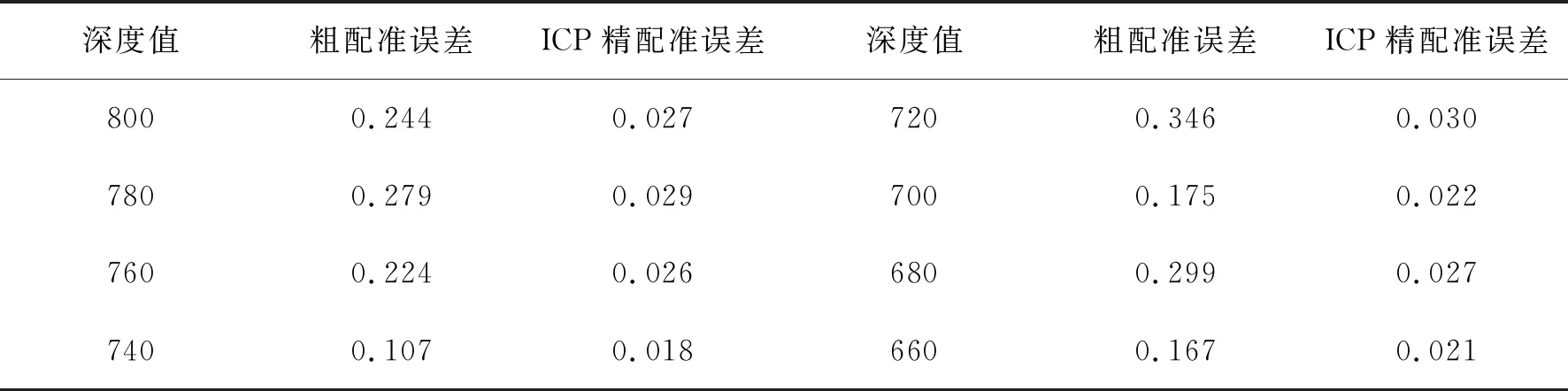
表1 不同深度平面的配准误差 (mm)

4.2 复杂表面配准实验

为进一步验证本文所提方法的配准效果，采用石膏像作为配准对象，进行两视角下的点云配准实验，配准后的结果如图3所示。

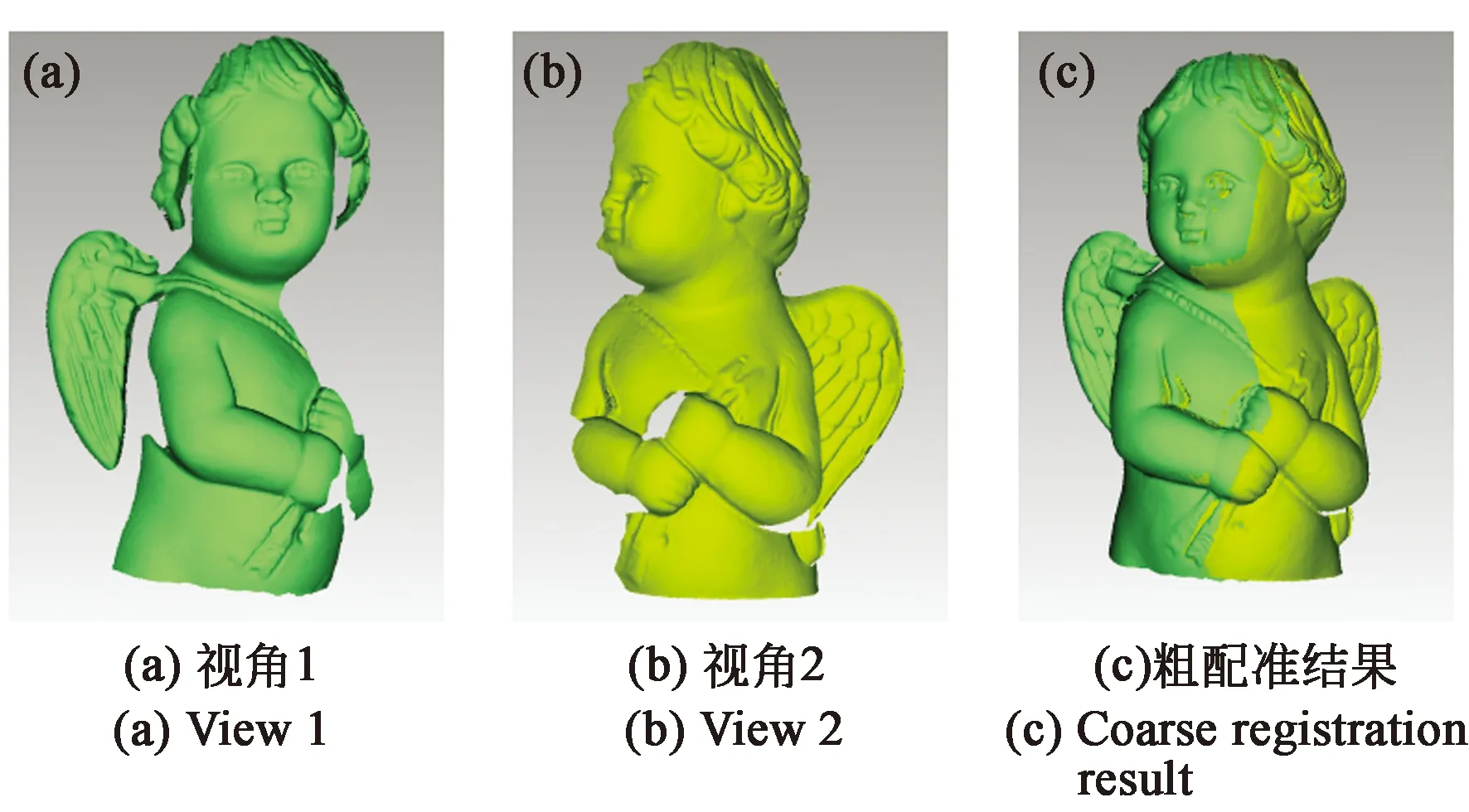
图3 石膏像配准结果

图3(a)和图3(b)为采用结构光三维测量方法获取的不同视角下的石膏像点云，图3(c)为采用本文所提粗配准方法进行粗配准后的结果。进行粗配准后，再结合ICP精配准方法进行精配准，精配准后的结果如图3(d)所示。从图中可以看出，精配准后的石膏像视觉效果良好。

精配准后的配准误差和迭代次数的关系如图4所示。可以看出，采用ICP方法进行精配准的配准误差，在迭代次数为10次左右时趋于收敛，配准误差约为0.04 mm。这也间接地表明本文所提粗配准方法可为ICP精配准提供良好的初值，使其在迭代过程中能快速收敛。

图4 配准误差和迭代次数的关系

5 结 论

本文提出一种基于电磁追踪系统的点云配准方法，利用电磁追踪系统发射器和接收器之间准确的位移和姿态角信息，获得坐标系转换矩阵，并提出一种基于平面的坐标系转换方法。配准实验结果表明，本文所提粗配准方法能够为ICP精配准提供良好的初值，使ICP精配准在迭代过程中能快速收敛，且配准后效果良好，精配准后石膏像的配准误差约为0.04 mm，验证了本文所提方法的有效性。但由于金属会影响电磁追踪系统的测量准确度，因此目前该方法主要适用于非金属物体表面的配准。