基于数学模型评估的再生水厂优化布局方法研究——以深圳市坪山河流域为例

马明敏 ，奚晓伟 ，王 浩

（1.中国市政工程西北设计研究院有限公司深圳分公司，518000，深圳；2.中国水利水电科学研究院，100038，北京；3.水安全与水科学协同创新中心，210098，南京）

深圳市坪山河流域内路网已经基本形成， 无法大规模在市政道路上新建污水管道。 上洋污水处理厂的用地扩建难度大，无地用于扩建。使用经过处理的污水于坪山河道补水时， 需建设庞大的污水收集和再生水回用管网系统， 包括多座污水提升泵站和再生水加压泵站， 将大大增加再生水回用成本。

本文通过建立数学模型，对污水处理系统布局进行分析和研究，以解决再生水回用、污水量增加带来的污水设施用地难以落实、 污水管网无布设空间等问题，从而提升市政基础设施的标准，为坪山河流域应对污水量激增带来的污水厂规划提供决策依据。

一、规划布局形式分析

城市污水再生回用一般可分为集中式污水再生回用、分散式污水再生回用和集中分散混合式污水再生回用3 种方式，3 种方式各有优点和缺点。 在实际应用时，须考虑再生水回用的经济性与合理性，通过污水再生回用布局优化确定回用方式。

二、研究方法的确定

以水环境质量达标为目标，根据污水处理厂布局规划方法现存问题，分析影响再生水布局的具体因素，提出以数学模型核定污水处理规模，确定相应模型，量化相关指标和方法。

1.临界距离概念

临界距离是指在某一规划区域内当污水收集和再生水输送费用等于该区域内污水处理再生和再利用综合成本时， 再生水输送的最远直线距离。 在再生水厂临界距离范围内的回用区应采用集中式再生回用，范围以外则采用分散式回用。

2.假设条件

再生水厂布局规划数学模型中的假设条件： ①不考虑地形条件，假设模型建立在水平面上；②不考虑管径大小，只考虑长度；③模型中的每个排放点位置，就是一个再生水厂的拟建位置；④对于一个排放点，其自身污水与其他排放点转输来的污水总量有两种处理方式，全部输送至下一个排放点或全部就地处理回用，即满足“全不处理或全部处理策略”；⑤污水回用各子系统工程使用年限相等。

3.优化依据

在规划区域内， 找到再生水厂规模和建厂位置的最佳组合，是城市污水再生回用布局的优化目的。即在相同的污水回用率下，追求整个地区的污水处理和回用的经济费用最小化。集中式再生水厂的建设成本主要包括厂内泵站的基础设施建设成本、污水和再生水管网基础设施建设的成本及增压泵站建设的成本。分散再生水厂的建设成本基本只包括厂区内的基础设施建设成本。如果集中式再生水厂的建设成本和污水管网及再生水管网的投资之和小于区域内所有分散式再生水厂的建设成本，则集中式布局供水模式比分散式布局经济，否则分散式更加经济。

4.最大综合经济效益

临界距离数学模型是在再生水系统的综合经济效益公式的基础上推导得出的， 区域内综合经济效益是指在工程服务期内相同规模的再生水工程分散式处理与集中式处理基础设施建设费用的差值。 从临界距离的概念看， 输送污水和再生水的管网费用等于规划区域内再生水综合经济效益时再生水管网所能达到的最远输送距离， 临界距离公式可通过下式推导得出：

式中，Em为区域综合经济效益最大值（万元）；Ckj为污水从收集区 k 到集中式再生水厂 j 的收集成本（万元）；Cjh为再生水从集中式再生水厂j 到回用区域h 的输送成本（万元）。

5.污水的收集费用

通常情况下，污水通过重力来实现收集和输送，当条件不足时需要增加泵站来提升。

污水收集费用=管网基础设施建设和后期维护费用+提升泵站基建和后期维护费用+提升泵站运行费用。

6.再生水的输送费用

再生水的输送费用=输送管网的基础设施建设和维护费用+增压泵站基础设施建设和维护管理费用+增压泵站运行的费用。

7.临界距离公式

临界距离公式为：

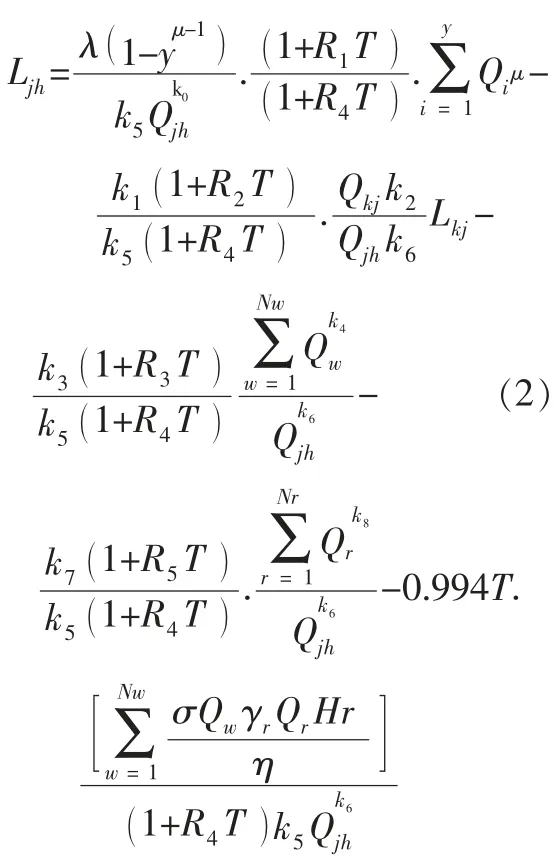
式中，Ljh为再生水输送的临界距离；Lkj为污水从收集区k 到再生水厂j的平均输送距离； T 为再生水厂的工程使用年限；Qi为分散式再生水厂的规模；Qj为集中式再生水厂规模；Qjh为从再生水厂j 到再生水回用区h 输送的再生水量；Qkj为污水从收集区k到再生水厂j 输送的污水量；Qr为第r座增压泵站最高日的规模；Qw为第w座污水提升泵站的规模；y 为分散式再生水厂的数量；λ 为在适用范围内的综合价格系数；μ 为在适用范围内的规模经济因素；R1～R5分别为再生水厂、污水管网、污水提升泵站、再生水管网、再生水增压泵站的年运行和维护费率，按照其基础设施建设费用的百分比取值；Nr 为再生水增压泵站的数量；γr为第r 座增压泵站供水能量的不均匀系数；Hr为第r 座增压泵站内水泵的工作扬程；ηr为第r 座增压泵站的工作效率系数；Nw为污水提升泵站的数量；ρ 为水密度；g 为重力加速度；Hw为第w 座污水提升泵站内水泵的工作扬程；ηw为第w 座污水提升泵站的工作效率系数；σ 为电价；K1～K8为方程式系数， 用最小二乘法求得。

三、再生水厂布局

坪山河流域根据《坪山河干流综合整治及水质提升工程》共规划设置了11 个补水点，分别为碧岭、沙湖、汤坑、大山陂、新和、飞西、赤坳、南布、墩子河、老河道和石溪补水点，补水点位置即为再生水回用区。

应用建立的临界距离数学模型对坪山河流域再生水厂布局进行优化， 确定坪山河流域再生水厂的最佳布局。 临界距离是表示集中式再生水厂与再生水回用区的距离关系，本次数学模型中的集中式再生水厂为上洋再生水厂（上洋再生水厂的扩建或改造）， 坪山河流域补水点为再生水回用区。 由于研究区域排水管网覆盖率较高，所以在集中式与分散式经济比较时可忽略污水输水费用，即令Cki=0。

参考北京工业大学齐晶瑶博士论文《城市污水再生利用的理论与方法》及相关资料， 参数取值为：T=25，α=173.7，β=0.83，P1=P4=P5=3.0%，k7=25.817， k8=0.9996，σ=0.55，γp=0.4，ηp=0.7，k5=122.5，k6=0.52，可计算：

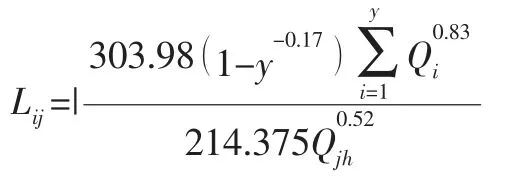
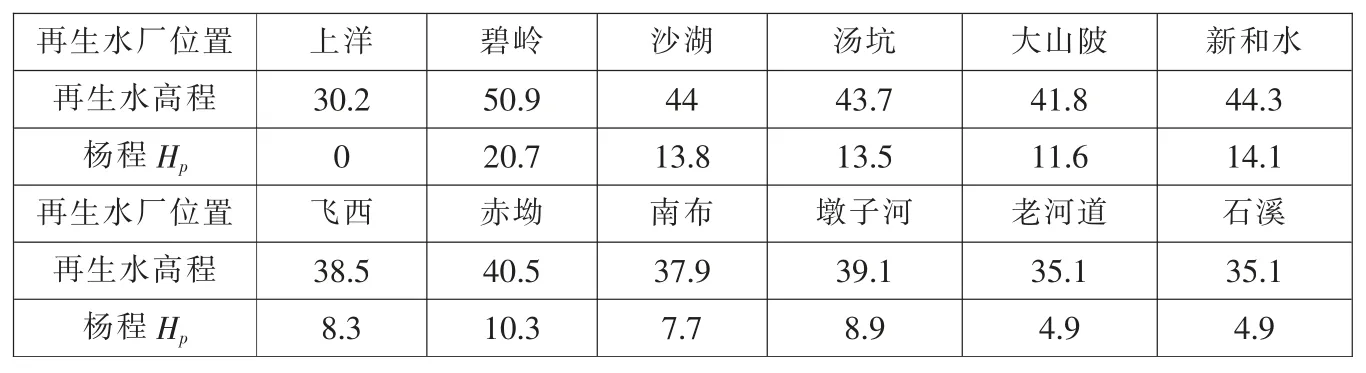
表1 再生水回用区提升泵站扬程计算 （单位：m）

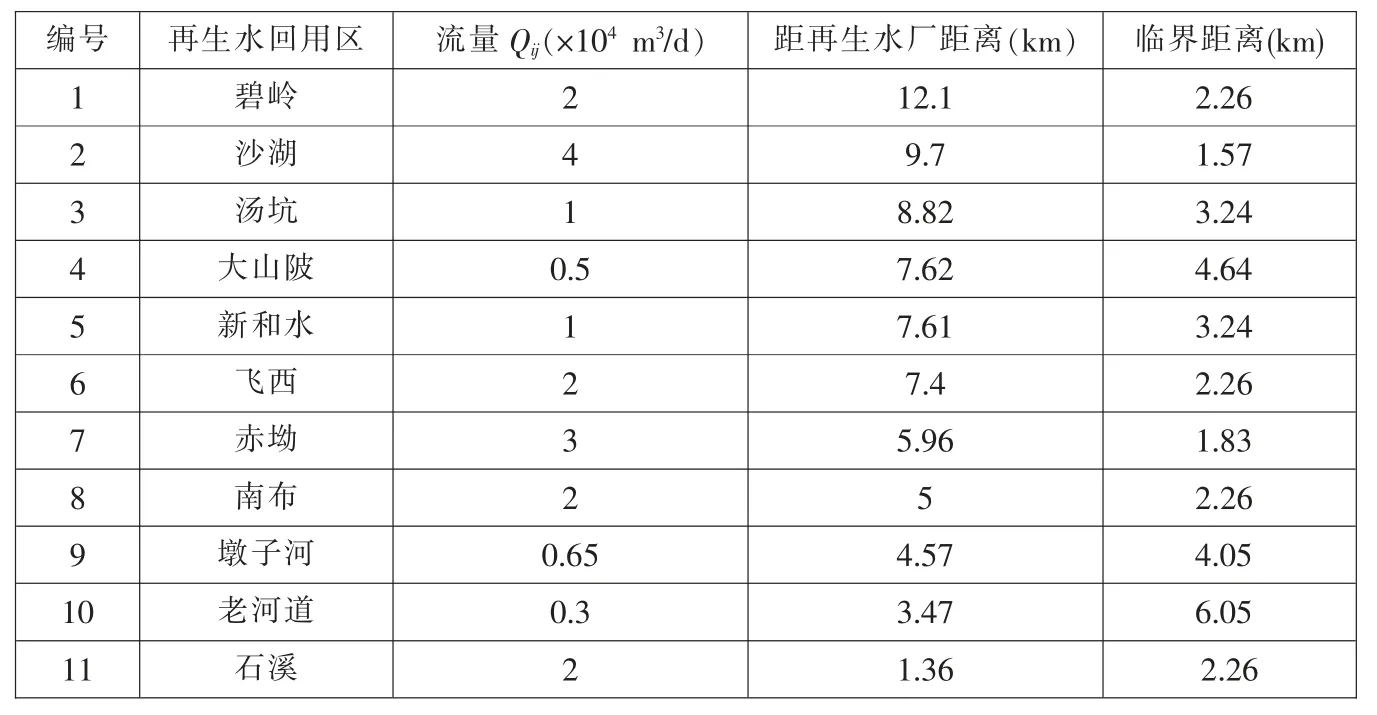
表 2 坪山河流域再生水回用区临界距离计算

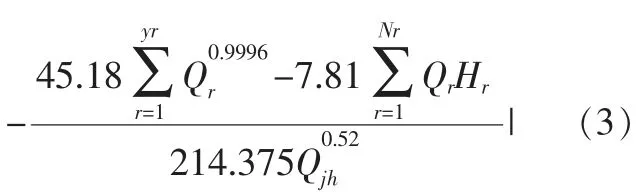
式中， 本次数学模型中再生水提升泵站流量Qp为各回用区的回用水量，也即之前论证过的分散式再生水规模，各提升泵站的扬程Hp为集中式再生水厂与再生水回用区的高程差，提升泵站的数量Np为11， 分散式再生水厂数量 N 为 11，Qij为各再生水回用区的流量。 再生水回用区提升泵站扬程计算见表1。

将以上数据代入式（3）后，可计算出Lij0， 计算后可知Lij0实际值为负值。 根据临界距离定义，表示本次分散式综合费用效益低于集中式综合费用效益。 说明坪山河流域再生水厂采用分散式较经济。

根据再生水需水量由式（3）计算各回用区的临界距离，计算结果如表2 所示。 可知，上洋再生水厂针对每个分散式再生水厂的服务范围为1.57～6.05 km， 以该服务半径画圆确定上洋再生水厂的服务范围，在服务范围内的再生水回用区，则可采用集中式污水再生回用，范围外则考虑分散式污水再生回用。 结合本次数学模型计算得出的结果，老河道和石溪可采用集中式污水再生回用，其余9 个补水点均需要建立分散式污水再生回用工程。