三峡升船机变频器IGBT开路故障诊断
孟令琦,高 岚,李 然,朱汉华
(1. 武汉理工大学 a. 船舶动力工程技术交通行业重点实验室;b. 能源与动力工程学院, 武汉 430063; 2. 长江三峡通航管理局, 湖北 宜昌 443002)
长江三峡工程是一项举世瞩目的跨世纪工程,三峡水利枢纽全平衡卷扬式垂直升船机是三峡水利枢纽的主要通航设备之一。[1-2]变频器作为升船机交流调速的重要环节,其主电路中绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)的开路和短路故障在变频器本身故障中占相当大的比例。相对短路故障而言,开路故障发生之后电机往往还能继续运行,该状态会引发其他IGBT过流,以致造成电机发热、绝缘损毁等严重后果。[3]目前,三峡升船机变频调速装置未能做到针对该类故障的故障检测,一旦出现故障,不仅会增加排故难度和维修成本,甚至会造成重大安全事故。因此,有必要开展三峡升船机变频器IGBT开路故障诊断研究,以达到降低排故难度,保障船舶安全通航的目的。国内外许多学者针对IGBT开路故障进行了相关研究,从故障检测信号的角度可分为2大类:一类为直接测取功率管的电信号参数;另一类为间接测取系统的输入和输出电信号参数。文献[4]和文献[5]分别以IGBT导通电阻的变化量和二极管的端电压作为故障检测信号;文献[6]和文献[7]分别以整流侧网侧三相输入电流和逆变侧三相输出电流作为故障检测信号。尽管直接测取功率管电信号参数能直接反映故障管所在的桥臂位置,但需安装大量传感装置,会增加系统的复杂性和维护成本。由于三峡升船机已安装对变频器的三相输入电流和输出电流进行传感监测的装置,考虑到诊断成本的经济性和研究成果的应用性,本文以变频器的三相输入和输出电流信号作为故障检测信号,基于希尔伯特黄变换[8]和电流均值法[9]间接提取信号故障特征,并通过概率神经网络完成故障分类,实现IGBT故障管定位。
1 三峡升船机变频调速系统
三峡升船机变频调速系统由8台交直交电压型变频器分别控制8台三相异步交流电机,通过调速实现升船机船厢的升降运行。本文基于1台变频器控制1台异步电机,进行变频调速系统的建模和诊断,系统结构主要包括变频器整流电路、滤波电路、逆变电路和负载侧的三相异步电动机(见图1)。

图1 变频调速系统结构
在整流或逆变电路中,均采用三相六桥臂脉冲宽度调制(Pulse Width Modulation, PWM)控制,整流侧电路结构见图2,IGBT分别位于A相、B相和C相上、下的各桥臂上。

图2 整流侧电路结构
在整流电路或逆变电路中同时出现3支开路的情形十分少见,但存在发生2支开路的可能性。因此,本文考虑发生双管故障的情况。经仿真研究发现:同种故障类型的三相电流波形因故障相序呈组合式排列;不同种故障类型的三相电流波形因故障管数量和故障上、下桥臂位置不同而存在差异。根据此规律将IGBT开路故障划分为6类。
1) 单管上桥臂故障:T1、T3、T5。
2) 单管下桥臂故障:T2、T4、T6。
3) 双管同侧上桥臂故障:T1T3、T1T5、T3T5。
4) 双管同侧下桥臂故障:T2T4、T2T6、T4T6。
5) 双管交叉侧桥臂故障:T1T2、T1T6、T3T2、T3T4、T5T4、T5T6。
6) 双管同相桥臂故障:T1T4、T3T6、T5T2。
2 IGBT开路故障特征分析
由于故障种类较多,考虑到整流侧与逆变侧均采用相同电路控制结构,只针对整流侧IGBT开路故障下多种故障类型中的1种进行故障特征分析。
2.1 IGBT开路故障机理
根据IGBT开关管的状态将整流侧三相输入电流的正常变化周期划分为6个工作区域,分别为:I区,330°~30°;II区,30°~90°;III区,90°~150°;IV区,150°~210°;V区,210°~270°;VI区,270°~330°,见图3。

图3 工作区间划分
将整流侧电路结构中控制每相桥臂IGBT开关管的状态定义为Sk,其中k为电流相序。当Sk置1时表示上桥臂开关管导通,下桥臂开关管断开;当Sk置0时表示下桥臂开关导通,上桥臂开关管断开。各工作区间开关状态分布见表1。
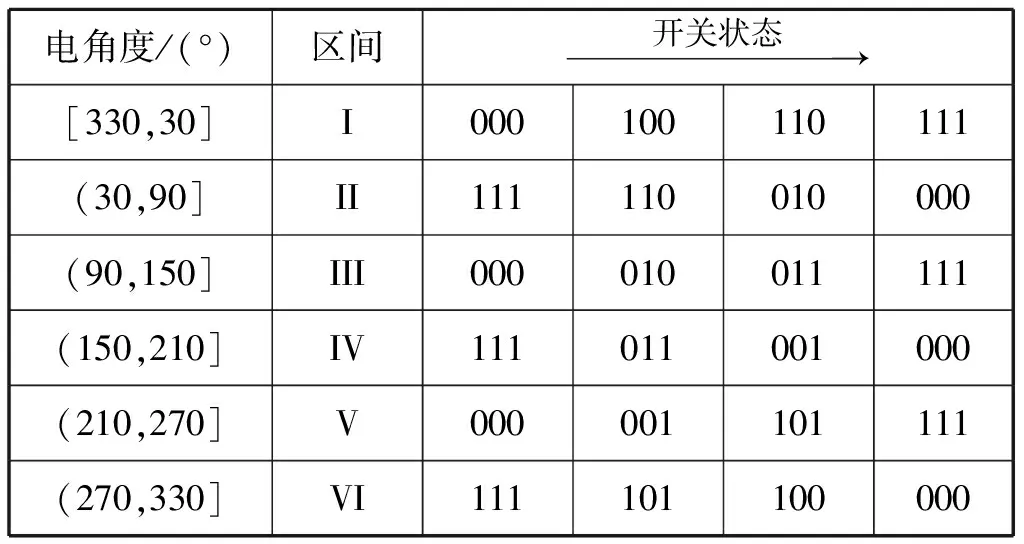
表1 各工作区间开关状态分布
2.1.1单管故障
当上桥臂T1发生开路故障时,在I区、II区和VI区ia为正向电流,由于T1开路只会对A相的负向电流造成断流影响,因此在A相电流单个周期内,其正半周电流波形没有出现断流现象(见图4);在III区、IV区和V区,由于电流为负向电流,T1发生开路势必会影响A相所需T1续流的正常状态。因此,在III区、IV区和V区开关状态为111时,将引起A相的断流;同时,由于网侧三相电流和恒定为零,导致其他两相电流激增。

图4 单管T1开路故障网侧三相电流畸变波形
当下桥臂T4发生开路发生故障时,在III区、IV区和V区ia为负向电流,而T4开路只会对A相的正向电流造成断流影响,因此在A相电流单个周期内,其负半周电流波形没有出现断流现象(见图5);在I区、II区和VI区,由于电流为正向电流,此时T4发生开路势必会影响A相所需T4续流的正常状态,因此在I区、II区和VI区开关状态为000时,将引起A相断流。由于T4在A相下桥臂上,与T1互为反相对称结构,T4与单管T1开路的三相电流故障波形反向对称,如见图5所示。

图5 单管T4开路故障网侧三相电流畸变波形
2.1.2双管故障
双管故障类型较多,实质上每种双管故障都是由任意2种单管故障复合而成的。考虑T1T4双管故障是由T1单管故障和T4单管故障复合而成的,选取T1T4双管故障进行故障机理分析。
当T1T4发生双管开路故障时,若是T1开路故障,势必在III区、IV区和V区开关状态为111时引起A相的断流;若是T4开路故障,必须在I区、II区和VI区开关状态为000时引起A相的断流。A相电流的正、负半周波形刚好对应单管T1和T4开路故障下的负、正半周波形(见图6)。由于故障管呈对称故障状态,引起的其他两相电流在正负半波的激增幅度变化相同。
2.2 IGBT开路故障特征分析
考虑到除了双管同相桥臂故障无上、下桥臂的区分之外,双管交叉侧桥臂故障类型中的每种故障都是由上侧桥臂和下侧桥臂复合而成的,故障波形的时域特征只与发生的故障相序相关,着重分析单管和双管同侧桥臂上、下桥臂故障的区分。选取单管上桥臂T1故障、单管下桥臂T4故障、双管同侧上桥臂T1T3故障和双管同侧下桥臂T4T6故障下的A相故障电流波形进行对比分析。

图6 双管T1T4开路故障网侧三相电流畸变波形
A相故障电流正负半波对比见图7。由图7可知:在单个故障电流变化周期内,由于在负向续流时发生断流,使得T1故障下的A相电流正半波的面积远大于负半波的面积,而T4故障下的结果与T1正好相反。与单管故障相比,在单个故障电流变化周期内,由于发生双管开路,使得在A相故障管进入正常续流区间时,B相故障管进入断流区,因而造成A相电流幅度激增,使得正、负半波面积差异减小。由于在单个周期内存在差异,随着时间的积累,差异会激增,因此可区分双管同侧故障的上、下桥臂。

a) 单管T1故障

c) 双管T1T3故障
通过计算三相电流的平均值构建区分上下桥臂的特征向量,计算式为
(1)
式(1)中:m为1个周期信号的总采样点数;k为A相、B相和C相中的某相电流;α为周期个数。通过计算得到电流平均值的正负,反映故障电流波形在正、负半周面积的差异,从而实现每相上、下桥臂的故障定位。
本文中α取值为10,m取值为100,在理想无故障状态下三相电流均值为(0,0,0)。由于实际工况下偏差的存在,将阈值设定在0.1时可满足有无故障的区分,构建桥臂特征量见表2,其中PA、PB和PC分别为A、B和C单相故障桥臂特征量。

表2 故障桥臂定位特征量
对于变频器逆变侧开路故障下的三相输出电流波形,同样可采取上述分析方法并构建故障桥臂特征向量,实现逆变侧每相故障桥臂的精准定位。
3 基于HHT的故障信号的特征提取
由于希尔伯特黄变换(Hilbert-Huang Transform, HHT)具有良好的时频聚集性,其核心是利用经验模态分解(Empirical Mode Decomposition,EMD),具有良好的自适应特性,可根据不同故障类型三相电流信号自身的时域波形特征进行分解。通过EMD分解得到的固有模态函数(Intrinsic Mode Function,IMF)分量能从幅度和频率上敏感地反映不同故障类型下三相电流信号之间的差异;同种故障类型下不同故障的三相电流时域波形随故障相序的不同呈组合式改变。因此,通过EMD分解得到的IMF分量组合也会有差异性。
3.1 基于EMD的故障电流信号分解
每种故障状态下三相电流信号中的每相电流信号都需进行EMD分解,这里对整流侧的单管T1开路故障、T4开路故障、同相桥臂双管T1T4故障、同侧上桥臂双管T1T3、同侧下桥臂双管T4T6和交叉侧双管T1T6开路故障下的A相故障电流进行对比分析。
截取以上开路故障下A相故障电流信号的时间长度为0.2 s,采样频率设置为5 000 Hz,共计1 000个采样数据点,分别将其作为初始信号I(t),按以下步骤完成对I(t)的EMD分解:
1) 信号初始化i=1,h0(t)=I(t) ,R0(t)=I(t)。
2) 求出hi(t)的局部最大值Nmax(t)和最小值Nmin(t)。
3) 使用3次样条函数,对极小值和极大值点进行插值,形成原数据序列的上、下包络线Smax(t)和Smin(t)。
4) 求解上、下包络线的均值Smean(t)。
5) 计算hi(t)=hi-1(t)-Smean(t),判断hi(t)是否满足IMF分量规则,即
(2)
式(2)中:一般SD为0.2~0.3,这里取0.26。当SD小于该值时,EMD算法就筛选出一个IMF分量fimf,i(t),否则重复步骤2)~步骤5)。
6) 将残差量Ri(t)作为新的初始信号从步骤1)开始执行,直到求出全部IMF分量。
最后,I(t)可由分解得到的IMF和一个剩余残差量构成,即
(3)
式(3)中:I(t)为初始信号系列;fimf,i(t)为1组从高频至低频的IMF分量;Ri(t)为残差量;n为IMF分量的数值。
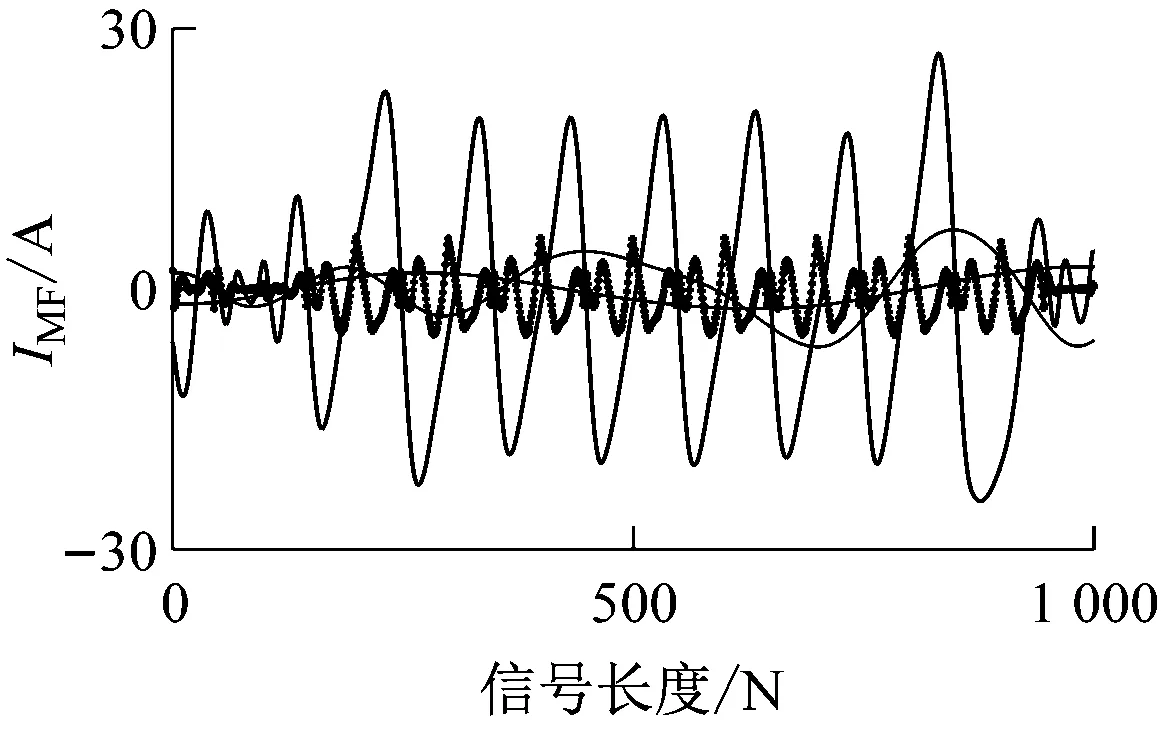
6种故障类型的A相电流EMD分解见图8,剔除各故障类型下A相电流EMD分解后的残差量和幅值极小的IMF分量。由图8可知:各故障类型下的IMF分量依次由高频带向低频带排列;相比第四阶IMF分量,前3阶IMF分量的幅值更高,中高频带的成分更多;不同故障类型之间,同阶IMF分量的幅度都存在差别。
同理,可按照上述方法对每种故障类型下的其他两相电流进行EMD分解。由于不同故障类型下不同相电流的时域特征差别较大,经过EMD分解得到的IMF分量阶数不同,需对不同故障类型得到的IMF分量进行频谱分析以提取特征频带。
3.2 基于HHT的特征频带能量熵提取
单管故障T1与单管故障T4下的非故障相B相和C相故障电流呈互补关系;双管T1T4故障下的非故障相B相和C相故障电流存在相位差,但波形变化一致;双管T1T3、双管T4T6和双管T1T6非故障相只有C相,其A相故障电流与B相故障电流呈互补关系。因此,着重对上述6种故障类型下的A相和C相电流进行基于HHT的特征频带能量熵提取。
对6种故障类型下的A相和C相电流进行EMD分解,得到的各阶IMF分量通过希尔伯特变换(Hilbert Transform)得到信号的Hilbert时频图简称Hilbert谱,记为

b) T4单管故障

c) T1T4单管故障

d) T1T3双管故障

(4)
式(4)中:ai(t)与wi(t)反映出不同阶IMF分量的幅值和频率随时间可变,其中i表示IMF分量的阶数。由此可得每个瞬时时刻的幅值和频率在整个幅值-频率-时间三维空间内的分布情况。
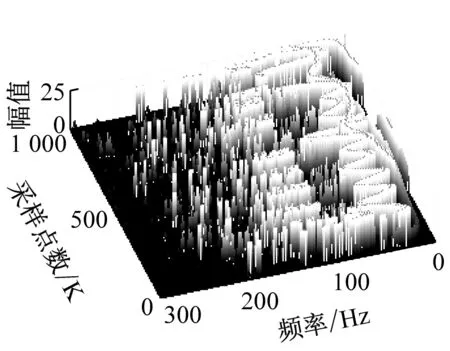
6种故障类型下A相电流和C相电流的Hilbert三维时频图分别见图9和图10,其中:纵轴反映信号在不同瞬时时刻下的幅度;时频二维平面反映出不同瞬时时刻分布的频带。
a) T1单管故障

d) T1T3双管故障
故障发生之后,6种故障类型下的A相和C相电流信号能量主要集中在0~300 Hz的频带上。在不同故障类型下,能量随故障时间分布在0~300 Hz频带的不同频段上,其中0~50 Hz、50~100 Hz、100~300 Hz频带上的能量随不同故障类型呈现出的分布状态差别明显。
根据划分的3条特征频带定义能量熵的计算式,其中3条特征频带的临界边界区间划分见表3。
每相电流下各特征频带能量熵的计算式为
(5)
式(5)中:fq为特征频带区间,q=1,2,3;k为三相电流相序;ai(j)和wi(j)分别为第i阶下IMF分量的瞬时幅值和瞬时频率;p为选择因数,当瞬时频率在其特征频带中时,p取1,否则取0。

a) T1单管故障

d) T1T3双管故障

表3 特征频带区间划分
由于不同故障类型对应的不同相电流特征频带的能量熵差异较大,对基于HHT的三相电流提取的3条特征频带的能量熵进行归一化处理,有
(6)
式(6)中:k和q分别为三相电流相序和特征频带序号;P(k,q)为每相电流各特征频带的相对能量熵。
整流侧6种故障类型的A、B、C三相电流特征频带的相对能量熵对比见图11。在同相电流下,不同故障类型下的3条特征频带的相对能量熵不同;在同种故障类型下,不同相电流的同一特征频带的相对能量熵不同。逆变侧6种开路故障类型同样能满足整流侧提取出来的3条特征频带,且具有相同规律的能量差别。因此,可将基于每相电流的3条特征频带的相对能量熵作为区分不同故障的特征量。

图11 三相电流3条特征频带相对能量熵对比
4 基于PNN的IGBT开路模式分类
IGBT开路故障诊断的最后环节是模式分类。传统的人工神经网络在进行模式分类时需采用启发式学习方法,以不断变更训练样本的方式重新训练网络。对网络的权值进行优化会花费较长的训练时间,收敛于局部的最优解使分类结果的准确度不高。与此不同,PNN是将贝叶斯(Bayes)决策分析放入人工神经网络框架中,将Bayes决策与无参估计概率密度函数相结合实现模式分类,无需设置权值和学习过程,训练速度快、效率高,具有强大的非线性分类能力。[10-12]
4.1 PNN模型的构建
本文对21种整流侧IGBT和21种逆变侧IGBT开路故障进行分类。由于整流侧和逆变侧采集的三相电流分属输入侧和输出侧。因此,分别建立整流侧的故障样本库和逆变侧的故障样本库,并各自按照1~21号的故障序号输出故障诊断结果。每种故障样本包含每相电流的3条特征频带的相对能量熵和每相故障桥臂的定位特征量,表示为
X=[P(A,1),P(A,2),P(A,3),PA,P(B,1),
P(B,2),P(B,3),PB,P(C,1),P(C,2),
P(C,3),PC]
(7)
基于PNN的故障诊断模型由输入层、模式层、求和层和输出构成,其网络结构拓扑图见图12。

图12 PNN网络拓扑结构
1) 输入层用于输入来自于整流侧或逆变侧每种故障样本X的12维数据,该层神经元个数为故障样本空间维数12。
2) 模式层基于整流侧或逆变侧故障模式的种类分成21类,每类神经元的个数取决于该类别训练样本的数量。计算出接收到的12维故障样本数据与模式层中第i类的第j个样本数据的欧氏距离。由于PNN为一种基于Bayes最小风险准则的径向基神经网络,因此模式层采用的激活函数基于Bayes准则,采用无参估计Parzen窗构建的高斯概率密度函数,即
(8)
式(8)中:i为21种故障类别数;d为故障样本空间的维数,本文取12;σ为Parzen函数窗宽度,即平滑因数;xij为第i类故障下第j个故障样本数据。
3) 在求和层对模式层中属于同一类模式下的经式(8)计算得到的各输出结果进行加权平均,有
(9)
式(9)中:vi为第i种故障的输出;L为每类模式下的样本数量。该层神经元个数和故障类别数相同,为21。
4) 输出层为最后一层,该层神经元个数与故障类别数相同,分别为每一故障类别的期望输出。每一输出层神经元接收来自于同模式类别下求和层的输出结果,并筛选出输出结果为最大值的输出层神经元,将其代表的故障类别输出。
4.2 故障诊断结果分析
考虑到故障种类较多,本文对整流侧21种故障模式进行故障诊断分析,并设立2组故障样本,即无故障桥臂特征量(d=9)和含故障桥臂特征量(d=12)。每组故障样本分别在每种故障模式下构建50个训练样本和100个测试样本。由模式层中的激活函数表达式可知:σ平滑因子代表高斯概率密度函数的标准差,设定值偏小或偏大都会对PNN的故障识别造成影响。
通过在2组故障样本中分别选取6种不同故障类型(即T1、T4、T1T4、T1T3、T4T6和T1T6的测试样本),以网络训练得到的故障诊断率为指标设置不同梯度试验,完成σ的最优选参,试验结果见图13和图14。

图13 d=9的故障诊断结果

图14 d=12的故障诊断结果
由图13和图14可知:含有故障桥臂特征量的故障样本的诊断率整体在90%以上,优于无故障桥臂特征量的故障样本的总体诊断结果。尤其是T1单管上、T4单管下、T1T3同侧双管上和T4T6同侧双管这4类上下桥臂区分明显的故障类型的诊断率显著提高。同时,σ对无故障桥臂特征量的故障样本的诊断结果影响较大:随着σ的增加,对于T1单管上、T4单管下、T1T3同侧双管上和T4T6同侧双管等4类故障类型的诊断结果,在σ=0.30或0.35时,可对这4类故障类型中的3类同时达到最优诊断结果。T1T4和T1T6双管故障的诊断结果较为稳定,其中T1T4的识别度最为理想。相反,带有故障桥臂特征量定位的故障样本受σ的影响较小,在σ=0.35时,各类型的故障诊断率已达到最优结果。最后,选择在σ=0.35并基于d=12(即含有故障桥臂特征量定位的故障样本)完成对整流侧其他故障模式的故障诊断,诊断结果见表4。

表4 整流侧21种故障模式诊断率
由表4可知:对于单管上、下桥臂故障双管同相桥臂故障下的每种故障可实现理想的区分,诊断结果达到100%;对于双管同侧上、下桥臂故障和双管交叉侧桥臂故障,存在少数误诊结果,但每种故障种类的诊断结果普遍达到95%以上,因此可满足对整流侧中21种IGBT开路故障的精准定位。
5 结束语
为降低三峡升船机变频器中IGBT开路故障的排除难度,保障船舶安全通航,本文重点针对三峡升船机变频器整流侧中的21种IGBT开路故障进行故障诊断研究,提出基于HHT提取三相电流信号特征频带的能量熵,结合三相电流均值的故障特征提取方法。最后,通过PNN对故障样本进行训练与测试,结果表明:该故障特征提取方法可实现对三峡升船机变频器IGBT开路故障的诊断,具有很好的工程实用性。

