年龄无关的生长模型研究—以落叶松平均高为例

国 红，雷渊才，郎璞玫

(中国林业科学研究院资源信息研究所，北京 100091)

了解和掌握森林资源的动态变化，对制定森林抚育经营方案和措施，促进森林质量精准提升具有重要的意义。森林生长模型是了解和掌握森林资源动态变化的一项重要工具。这类方程的形式很多，可以分为理论生长函数、经验生长函数和Box-Lucas 生长函数，而著名的理论生长函数有Richards模型，Schumacher 模型，Schnute 模型等[1-3]。这些模型一直被广泛应用，如模拟树高生长，优势高生长，断面积生长等。森林生长模型在构建和应用研究中，通常使用年龄作为重要因子，但林木年龄因子往往存在两方面的问题，一是测定困难，一般需要用生长锥测定具有清晰年轮树种的从髓心开始的整个年轮的数据，对于没有清晰年轮的树种，测定往往非常困难，而绝大多数阔叶树不具有清晰的年轮；二是年龄不一定有效，在树木年龄差异较大的林分中，年龄不能用于预测林木或林分生长和产量，特别是对于天然林的生长和动态监测更加依赖于年龄无关的生长模型。因此，年龄无关的森林生长模型的研究变得越来越必要。

国内外许多学者开展了一些与年龄无关的森林生长模型的相关研究。Martin 等[4]，Monserud 等[5]，Trasobares 等[6]通过使用与年龄无关的经验线性模型模拟了单木的生长，但是这类模型可能不能确保单木或林分生长有适合的生长曲线特性，即生长曲线达到最大生长量后生长逐渐下降。而应用理论生长函数这个特性进行外推预测林木生长时，可以保证单木或林分的生物学特性。

Vanclay[7-8]考虑单木或林分生长曲线的生物学特性，构建了具有这种性质的线性经验函数，并已经被许多作者成功地使用。这类生长函数的表达式如下：

其中Y 为林木变量生长量，dY 和dt 为林木变量生长率，k 可以取为1 或2，常数β0可以表达为环境变量和(或) 竞争变量的函数。然而，这些参数没有特定生物学意义的含义。

Huang 和Titus[9]为了模拟阿尔伯达北部混交林中白云杉(Picea glauca (Moench) Voss) 的直径增量生长变化，比较了前面生长函数的非线性形式与能描述单木或林分生长曲线形状的非线性Box-Lucas 函数，结论是Box-Lucas 函数模拟直径生长效果比非线性的经验生长函数好。Box-Lucas 函数表达式为：

其中：θ1和θ2是估计增量曲线形状的参数，dY 和dt 为林木变量生长率。这些函数和其他类似的函数可以用来对单木或林分变量的增量进行建模。这些参数也不具有特定生物学意义的含义。

理论生长函数通常建立在公认的生物学关系的基础上，因此它们的模型参数可以从生物学的角度进行解释。不管树种和林分类型，树木的生长都遵循某种S 型或凸型生长曲线，它显示出树木寿命的3 个阶段。模拟树木和林分生长的一种非常成功的方法是使用用差分方程表示的生长函数，如Bailey 等[10]和Borders 等[11]提出的，已被许多学者使用[12-14]。差分方程表示一组生长函数，除了一个“自由” 参数外，所有参数都是公共的。但多数这类差分方法并没有隐去年龄。Tomé等[15]利用隐去年龄的差分方法将Lundqvist 模型和Richards 模型分别应用于葡萄牙桉树优势高生长和软木栎胸径生长的研究；Gea-lzquierdo 等[16]基于Hossfeld IV 和korf模型的差分形式模拟树木直径的生长。葛宏立[17]以Johnso -Schumacher 模型为基础，导出年龄隐含的模型应用于森林资源连续清查数据的生长研究，邹奕巧等[18]用丽水市的马尾松样木胸径数据，导出了Richards 模型隐去年龄的形式，并采用单点估计法和双点估计法2 种方法进行研究。但是，此类研究目前为止相对较少，而且这些研究往往没有或者较少考虑到环境因子对于生长的影响。本研究以理查德模型为基础研究隐含年龄的差分形式，并建立差分方程的系数参数与环境因子和林分因子的相关函数，以便更好的解决年龄不可及或者不是有效变量的问题和更全面解释单木和林分生长的生物学特性，为混交林质量精准提升提供一种有效的经营工具。

1 材料和方法

1.1 材料

研究采用2004 和2009 年吉林省两期177 块落叶松固定样地数据，测量间隔为5 a。固定样地为20 m×30 m，主要调查因子有胸径、林分年龄、平均树高、郁闭度、地位级、坡位、坡向、坡度、海拔高度、土层厚度和土壤类型等（见表1）。落叶松样地的选取原则是树种组成中，落叶松的胸径断面积超过70%，平均高通过每块样地3 株平均木的树高取平均得到，平均年龄通过生长锥钻取3 株平均木的树芯计算的年龄平均值得到。研究区气候数据从WorldClim 数据库下载得到（网址：www.worldclim. org）。每个样地可以下载19 个用于构建气候敏感的生物量模型的候选气候因子（表2），分辨率为1 km×1 km。这些因子可以分为两大类，即温度有关的变量10 个和降水量有关的变量9 个。每个气候因子是1990—2000 年的平均值。

表1 林分和气候因子 Table 1 Stand and climate factors

利用双重筛选逐步回归方法，建立两期平均高和19 个气候因子的线性关系，入选的因子为最湿季度的平均温度BIO8、年降水量BIO12 和最湿季度的降水量BIO13，这3 个气候因子在建模中最为敏感，本研究予以选用。具体含义见表2。

表2 入选气候因子含义Table 2 Implications for selected climate factors

1.2 方法

理查德方程认为一个器官的生长可以表达成有机物合成和降解之差。假设合成可以被表达成质量的异速生长关系，而降解和质量是成比率的，因此生长可以被表达为：

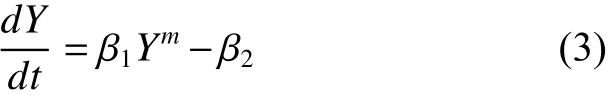
式中：β1、β2和m是参数。生长方程是不基于年龄的，因此对于异龄林样地或者年龄未知的异龄林样地数据结构模拟单木或林分生长是非常适用的。实际应用中，上式瞬时生长量用单木或林分收获量表达即形式可以由式（3）积分为：

式中：参数可以分别由下式表达：

A是当t趋于无穷时的渐近线，k是和生长率相关的参数，m是形状参数。c= e-kt0，t0是Y=0 时的年龄。大多数应用中，如果t0=0 时C=1。这里取C=1.

与年龄无关的差分形式可以通过类似于通常用于将生长函数公式化为差分方程的方法(如Amaro等[12]的过程来获得）。考虑到吉林省177 块天然落叶松林的连续清查数据缺乏年龄，为了建立单木或林分的树高生长模型，本研究基于理查德方程（4）推导不含年龄的差分生长方程。根据式（4），第i年和第i+a年的平均高为：

在这里，a为预测期，或为连续清查时间间隔，Yi+a是预测期（或连续清查时间间隔）的单木或平均高，Yi是连续清查时间初期的单木或平均高，A是当t趋于无穷时的渐近线，k是和生长率相关的参数，m是形状参数。式（12）表达比较复杂，但是当拟合单木树高或平均树高生长时参数很容易收敛。

为了模拟平均树高生长，本研究分别尝试采用k为固定参数和自由参数两种形式。也考虑了m为自由参数的情况，但获得的结果是m受林分因子、气候因子的影响不明显。当k为自由参数时，将k表达为林分因子和气候因子的线性函数关系。

其表达形式分别有如下4 个形式，并进行比较。

在这里，b0～b5是估计参数，BA是样地断面积，S是土壤厚度，BIO8 为最湿季度的平均温度，BIO12 是年降水量，BIO13 是最湿月份的降水量。

1.3 模型检验

选择平均误差(e¯)，均方根误差(RMSE)，总相对误差(TRE)，确定系数(R2)4 种统计量来检验模型的拟合优度和误差，并观察残差分布是否有异质性。利用修正确定系数AjustedR2对模型进行检验和评价（式22）。

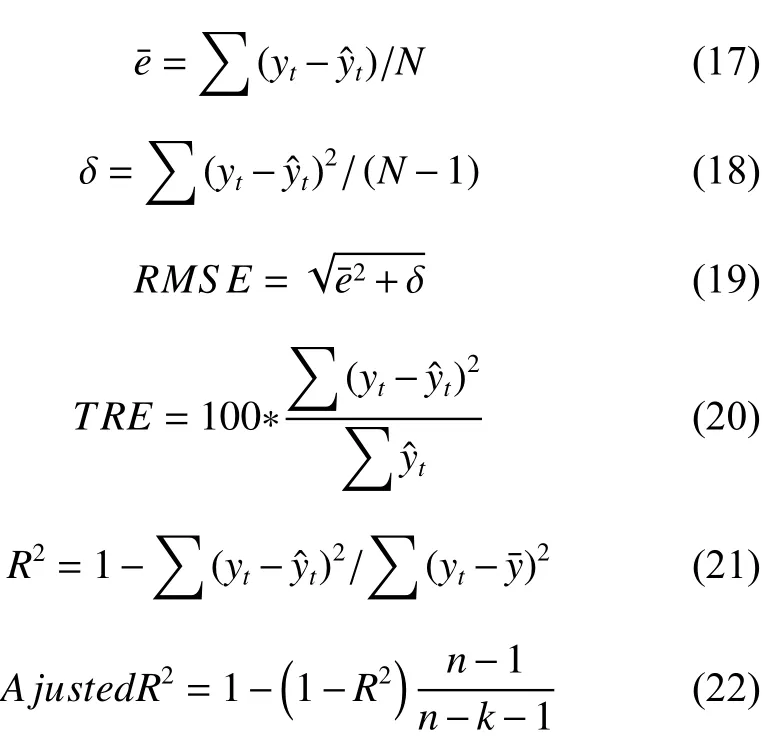
1.4 模型比较

对模型间的差异采用F 统计检验，F统计指标按照下式计算：

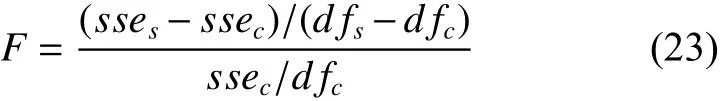
其中：sses和dfs分别为Richards 模型1 的回归模型残差平方和和自由度，ssec和dfc分别为Richard模型2 的回归模型残差平方和和自由度。

利用上式计算的F值与自由度分别为dfsdfc和dfs的F临界值进行比较，以确定两个模型之间是否存在显著差异。

2 结果

表3 是利用最小二乘法拟合的模型式（13）～（15）、式（12）和式（4）的参数值。从表中可以看到，所有模型的渐近线A值在17.53～22.72 之间，年龄无关的平均高生长模型式（13）～（15）和式（12）的渐近线在21.85～22.72 之间，更符合落叶松最大高的实际情况。而年龄相关的模型式（4）的渐近线只有17.53，明显偏低。

在表4 中，利用刀切法对模型进行验证，每次从建模样本中随机抽取50% 的样本，使用同一模型拟合，重复10 次，进行模型参数的灵敏度分析来评价模型；拟合结果使用验证样本年龄无关的模型式（13）～（16）和式（12）的修正确定系数在0.92～0.94 之间，而年龄相关的模型修正确定系数为0.85，时间无关的模型修正确定系数提高了8%～10%；模型式（13）～（16）和式（12）的均方根误差RMSE在1.30～1.59 之间，远远小于年龄相关的模型式（4）的20.48。如图1a 和图1b 所示，时间和平均高的关系很难用一条曲线来描述，而用年龄无关的模拟拟合的平均高和实测平均高相关系数却高达0.97。

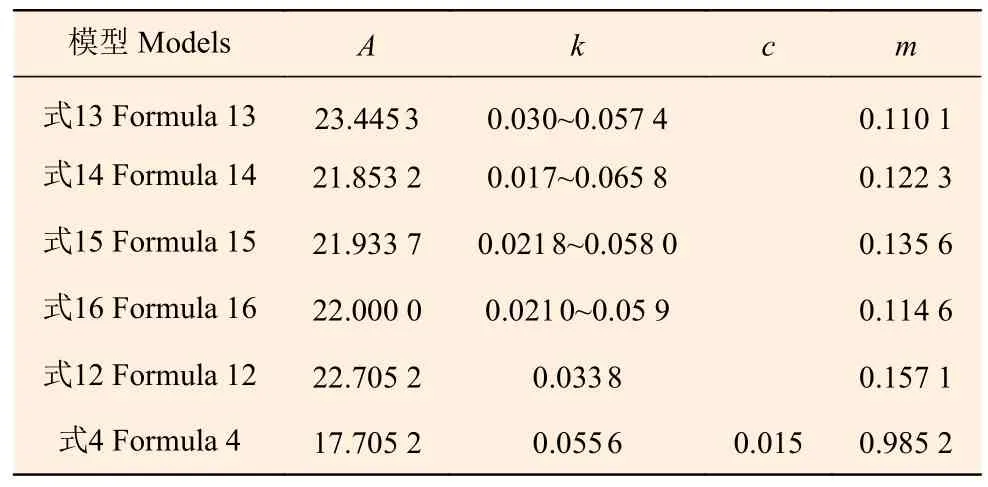
表3 模型参数Table 3 Model parameters

表4 线性函数参数Table 4 Parameters of linear function

年龄无关的几个模型进行对比，从表5 的F值来看，F0.05在2.42～3.89 之间，F值在0.15～81.05之间。从表中可以看出，模型式（15）和式（16）的F值是0.15，F0.05是3.89，说明这两个模型差异不显著；同样模型式（15）和式（13）的F值是2.98，F0.05是3.89，说明这两个模型差异也不显著。其它模型两两对比，都差异显著。

模型式（13）和式（14）对比，式（14）引入了气候因子，气候因子的选用参考了José Tomé等[12] 的文章，从F值来看，差异显著，同时式（14）的修正决定系数0.941 9，也高于式（13）的0.935 2（表6），而式（14）的均方根误差RMSE和TRE较式（13）也有明显的降低，说明气候因子的引入提高了模型的模拟效果。图2 是6 个模型的残差分布图，从图上看出年龄无关的模型（式12～16）的残差分布均优于年龄相关的模型(式4)。

图1 a 时间和平均高的关系图 ，b 模型式（16）实测和预测数据关系图Fig. 1 a The relationship between mean height and Age b The relationship between fitting data and measured data of formula 16

本研究在模型式（13）～（16）中采用自由参数k的形式，将k表达成立地因子和气候因子的线性形式，而模型式（12）采用固定参数的形式，对比两类模型发现，模型式（13）～（16）的修正可绝系数均大于式（12），而误差均小于式（12）。

3 讨论

本研究基于Richards 函数建立了年龄无关的差分方程，从而可用于年龄未知或者年龄不是有效因子的情况下的林分。选择年龄已知的固定样地，对比了年龄无关模型和年龄有关模型的模拟精度。年龄无关的生长模型比年龄相关的模型精度高而误差小。葛宏立等(17)采用年龄无关模型方法研究马尾松生长模型时预测精度高达99.80%，高东启等[19]用年龄无关的模型拟合蒙古栎生长，模型的R都大于0.98，预估精度在99.40%～99.72% 之间，邱思玉等[20]分别用不同的年龄无关树高模型建立优势高模型也得到了较高的预估精度，研究结果与本研究基本一致。分析原因，可能是因为年龄无关的生长模型直接以单木自身的观测值为自变量来预测后期的生长情况，这在一定程度上淡化了林相、立地、竞争等因子的影响。

表5 模型F 值Table 5 F parameter of models

表6 模型统计值Table 6 Model statistics

另外，从拟合得到的渐近线来看，年龄无关模型拟合的渐近线更符合落叶松高的实际情况，分析原因，作者认为一方面年龄无关的模型具有较好的预测能力。另一方面外业调查获得的林分年龄存在一定的偏差，这也和年龄因子难于获得有关。

图2 模型残差分布图(a. 式12, b. 式13, c. 式14, d. 式15, e. 式16, f. 式4)Fig. 2 Distribution of residuals errors (a. Formula 12, b. Formula 13, c. Formula 14,d. Formula 15, e. Formula 16, f. Formula 4)

同时，本研究采用自由参数的方式将与年龄无关的立地因子和气候因子引入模型的拟合中，对比固定参数和自由参数的两类模型，可以发现自由参数的模型表现更好。因此认为参数k 与立地因子和气候因子相关性强，这和Tomé等[15]的结论一致。引入气候因子的模型比仅引入林分因子的模型表现更好，说明考虑气候对生长的影响更有利于优势高生长的模拟。

但是，以5 a 为预测间隔期是比较短的，树木生长短期内不会有太大的生长变化，使得模型的预测误差较小，从而保证了模型有较高的预测精度。模型仍然需要三期及以上的数据进行进一步的检验，从而分析在年龄间隔较大时能否保证较高的预测精度。