Simulation-based correction of dose enhancement factor values in photon brachytherapy with metal nanoparticle targeting
Slobodan Milutinovic´ · MilosˇVujisic´
Abstract The purpose of this study is to investigate and quantify the influence of nanoparticle composition, size,and concentration on the difference between dose enhancement values derived from Monte Carlo simulations with homogeneous and structured geometrical representations of the target region in metal nanoparticle-enhanced photon brachytherapy. Values of the dose enhancement factor(DEF)were calculated for Pd-103,I-125,and Cs-131 brachytherapy sources with gold, silver, or platinum nanoparticles acting as targeting agents. Simulations were performed using the Geant4 toolkit with condensed history models of electron transport.Stringent limits were imposed on adjustable parameters that define secondary electron histories,so that simulations came closest to true event-byevent electron tracking, thereby allowing part of the nanoparticle-laden volume used for calculating the dose to be represented as a structured region with uniformly distributed discrete nanoparticles.Fine-tuned physical models of secondary radiation emission and propagation, along with the discrete geometrical representation of nanoparticles, result in a more realistic assessment of dose enhancement.The DEF correction coefficient is introduced as a metric that quantifies the absorption of secondary radiation inside the nanoparticles themselves, a phenomenon disregarded when the target region is treated as a homogeneous metal—tissue mixture, but accounted for by discrete nanoparticle representation. The approach applied to correcting DEF values both draws from and expands upon several related investigations published previously.Comparison of the obtained results to those found in relevant references shows both agreement and deviation,depending on nanoparticle properties and photon energy.
Keywords Monte Carlo · Brachytherapy · Nanoparticles ·Dose enhancement · Geant4
1 Introduction
For the past two decades,the use of metal nanoparticles(MNPs)as selective radiosensitizers in photon radiotherapy has been investigated extensively. Owing to their high atomic number and density, MNPs absorb more X-rays or gamma rays than the surrounding tissue. When introduced selectively into a target volume, which can even be a subcellular structure such as the cell nucleus, MNPs enhance local energy deposition by way of short-range secondary radiation (secondaries) produced in them by the primary photons. This improves the therapeutic ratio of radiotherapy by directing the deposited energy to desired targets (e.g., the DNA molecule) and sparing the surrounding structures from unwanted radiation effects.Interest in the radiosensitizing potential of MNPs is a part of broader ongoing research that strives to put many unique properties of nanoparticles to use in medical applications[1—5]. The high X-ray attenuation and general biocompatibility of many MNPs, for example, also make them applicable as contrast agents in medical radiography. The combined therapeutic and diagnostic potential of MNPs has been investigated in the newly established field of nanotheranostics [6—9].
Over the years, investigation of dose enhancement in photon radiotherapy by means of some incorporated high-Z material went from considering iodine (which was already being used as a contrast agent in radiography)[10—12], to studying metallic foils [13] and microspheres[14], to finally looking at metal nanoparticles, which, in elemental form, surface-coated or functionalized, yielded the best targeting specificity and radiation dose localization[15, 16]. An important part of these preclinical studies is the use of Monte Carlo simulations that yield values of the absorbed dose in tumors with incorporated MNPs. These numerical experiments are used to assess the gain in therapeutic efficacy due to the targeted introduction of MNPs.Because biological structures that can be targeted by nanoparticles are on the micro- to nanoscopic scale, the simulations need to implement concepts of nanodosimetry[17].
As the technology of nanoparticle production and engineering advanced [18—20] and first promising animal in vivo and in vitro experiments using MNPs for radiation treatment of tumors were conducted[21—23],investigation focusing on the nanodosimetric aspect of radiation therapy intensified [24—29]. The first simulation-based studies that tried to shed light on the dose enhancement capabilities of MNPs modeled the target tumor site as a metal/tissue mixture. Discrete geometrical representation of nanoparticles in simulations called for ever more detailed modeling of radiation transport, which could yield distributions of deposited energy over nanometer ranges. The significance of the track structure (or event-by-event) approach to radiation transport simulation for nanodosimetric calculations was recognized at least two decades ago [30—36].
In general, Monte Carlo simulations that calculate the dose enhancement factor (DEF), defined as the ratio of absorbed dose in a target volume with nanoparticles in it to that without, fall into two broad classes: one that models the tumor loaded with MNPs as a homogeneous mixture of tissue and metal[37—40],and another that models MNPs as distinct entities (usually nanospheres) inside the tumor volume [41—54]. Studies of the latter kind investigated radiation energy deposition patterns around a single nanoparticle in various irradiation scenarios [42—45],assumed a certain distribution (often uniform) of NPs within the target volume [41, 46—51, 54], or considered clusters of NPs [52, 53]. Since the loss of deposited radiation energy to the NPs themselves is neglected by the homogeneous representation, it tends to overestimate the DEF.Discrete nanoparticle representation is more accurate in this respect, but requires optimization of computer resource management, which makes the modeling stage somewhat more complex,and the simulation runtime much longer even when optimized.
The fact that part of the deposited energy stays within the nanoparticles themselves has been examined in some simulation-based investigations. The results showing that DEF values obtained from simulations that modeled the presence of MNPs as a metal/water or metal/tissue mixture are overestimations can be found in several papers[41, 46—48]. This was sometimes expressed as an observation that DEF showed a nonlinear dependence on nanoparticle diameter or volume, which was attributed to secondaries being absorbed more readily in NPs of increasing size. All of these studies relied on existing simulation models of radiation interactions,as encountered in commonly used Monte Carlo packages, which, to this day, still do not perform event-by-event electron tracking in solid media, but rely on condensed history models of electron transport [55—57]. The reported degrees to which DEF is overestimated by the mixture approach refer to disparate particular cases and are somewhat inconsistent throughout previous research. These inconsistencies, apart from reflecting different beam qualities and target geometries, sometimes stem from insufficiently substantiated choices of values for the adjustable parameters in the physical models underpinning the simulations.
The purpose of this paper is to utilize condensed history models of electron transport,presently implemented within the Geant4 Monte Carlo toolkit [58, 59], for finding corrections to the DEF values obtained with the mixture approach in simulations of photon brachytherapy treatments. The starting point was to examine how to best adjust the parameters of condensed history-based physical models to arrive at the most reliable dose estimates within reasonable computation times. Adjustable simulation parameters, such as energy cutoffs and step sizes, were optimized to make the physical models of radiation transport pertinent to the discrete representation of MNPs inside a region in which the dose is calculated. The difference between the DEF values derived from homogeneous (i.e.,mixture) and structured (i.e., discrete) geometrical representations of MNPs was investigated for three common brachytherapy sources (Pd-103, I-125, and Cs-131) and three MNP types (gold, silver, and platinum) of various diameters and concentrations. The validity of the applied approach is examined through comparison with results from previous studies, which showed both agreement and deviations, emphasizing the necessity of fine-tuning the bounds of simulation models.
2 Materials and methods
While fully discrete models of electron transport in gold and other metals are still being developed and tested[60, 61], it is instructive to push the available algorithms already implemented in Monte Carlo simulation toolkits to their limits in treating the case of discrete MNPs distributed in a volume of interest. The present study uses the Geant4 Livermore condensed history algorithm for electron transport to calculate the dose at the nanoscale. To make the results obtained from this algorithm as precise as possible,the parameters that define it (namely, the production cut,step-size limit,and lowest electron energy,defined in Sect.2.4) were set at values that bring it as close as possible to true event-by-event particle tracking.The price to pay with this approach is the computation time needed to complete such simulations. With this in mind, the influence of varying these adjustable parameters on result variability and computation time was scrutinized in advance,and a set of optimal values adopted, which were then used throughout the actual simulation runs that produced dose values.
Precision in dose calculations is needed because the aim of this study is to investigate the difference between two approaches to nanoparticle representation in Monte Carlo simulations. The first of these approaches represents the entire target volume into which the MNPs are introduced as a mixture (i.e., a homogeneous blend) of metal (from which the nanoparticles are made) and water (acting as a tissue substitute). In the second approach, a water-filled subregion of the target volume contains MNPs represented as distinct nanospheres distributed uniformly within it. In both cases, only this subregion (the one that differs in structure between the two approaches) is used as a dosescoring volume in simulations (see Sect. 2.2).
The mixture representation treats the target volume as having a density that is a weighted average of its components’ densities, and the same applies for the attenuation coefficient (i.e., for its photon absorbing properties). For this approach, the dose enhancement factor (DEF), which is a standard figure of merit when assessing dosimetric gain in studies of radiosensitization by targeted/selective introduction of nanoparticles,is defined as the ratio of absorbed doses deposited in the target volume with and without the metal component, under identical irradiation conditions. It is evident that in this case, while the presence of metal in the mixture does add to the overall photon absorption,DEF overestimates the real dosimetric benefit,since it inevitably disregards the fact that part of the deposited energy stays within the nanoparticles themselves, never reaching the surrounding tumor tissue or any of the specifically targeted subcellular or intranuclear structures.
Structured representation of a subregion in the MNPloaded volume, on the other hand, offers an opportunity to calculate the energy deposited inside the nanoparticles separately from the energy that is actually deposited in the medium surrounding the MNPs. Notwithstanding that ranges of secondaries originating in the MNPs, through either photon or electron interactions,differ in metal and in surrounding water (or tissue), Auger and delta electrons typically have sub-micron ranges (often just up to a few nanometers or tens of nanometers), photoelectrons can travel up to hundreds of microns, while characteristic X-rays can travel as far as centimeters.Partial deposition of radiation energy within the nanoparticles may be due to self-absorption (when some of the energy carried by the secondaries stays in the nanoparticle in which they appear before they leave it), crossfire (when secondaries originating from one NP reach another and deposit some of their energy there), or influx (secondaries originating in the surrounding medium, water or tissue, enter or cross a nanoparticle and deposit part of their energy there). The relative contributions of these three deposition pathways are expected to depend on the diameter and concentration of nanoparticles.
To quantify the influence of nanoparticle composition,size, and concentration on the difference between dose enhancement values calculated with homogeneous and structured geometrical representations of the nanoparticleladen dose-scoring subregion, the DEF correction coefficient is introduced in Sect. 2.1 as a metric that reflects the absorption of secondary radiation within the nanoparticles.Section 2.2 goes on to deliberate the geometry used in the simulations, including the shape and dimensions of the target region,and structural parameters that refer to MNPs.The properties of radiation sources and fields used in the simulations are reviewed in Sect. 2.3. Details on the adjustment and adoption of values for parameters in physical models of radiation interactions are outlined in Sect. 2.4.
2.1 The correction coefficient (r)
Let mtbe the tissue mass in the region of interest and mnpthe total mass of nanoparticles introduced into this region. The ratio of these two masses k = mnp/mtdenotes the concentration of the introduced metal nanoparticles,commonly expressed in units of [mg metal/g tissue] (i.e.,milligrams of metal per gram of tissue), or alternatively[mg metal/g water] if water is taken as a tissue substitute.
The absorbed dose deposited in the tissue without the NPs is:
Monte Carlo simulation runs with different representations of the region of interest—homogeneous or structured—and all other parameters kept the same produce values of deposited energies Emixand Et,respectively.The DEF correction coefficient is then obtained from Eq.(6)for each specified size and concentration k of MNPs,over three radiation sources.
2.2 Geometrical model
The model of the nanoparticle-loaded tumor region(i.e.,the treatment volume) consisted of two parts, as shown in Fig. 1. Central subregion of the simulation space is a cube in which scoring of the deposited energy was performed.It is embedded and centered within a larger cubic volume.The inner cubic volume had either metal/water mixture in it, or spherical MNPs distributed in water, the two cases corresponding to homogeneous and structured representations of the dose-scoring subregion, respectively. In the structured representation, all nanoparticles were of equal size in a single simulation run, and the diameter of nanoparticles ranged from 10 to 400 nm throughout various runs,while the concentration k took values from 0.1 to 50 mg of metal per gram of water. To determine a single value of the correction coefficient r for specific nanoparticle diameter and concentration,two simulation runs were required, using the two different representations of the inner cube medium. The run with a homogeneous inner cube would produce as output the value of Emix, while the run with a structured inner cube would yield Et.
The outer cube,enveloping the inner one,was filled by a homogeneous mixture of metal and water across all simulation runs,with a metal concentration equal to that of the inner cube in each run. The size of the outer cube was established based on the CSDA range of 40 keV electrons in water, which is 29.19 μm. [62] The most energetic secondary electrons that can appear for the three considered radioactive sources are photoelectrons created by 39.748 keV gamma rays from Pd-103(see Table 1 in Sect.2.3). Therefore, the adoption of a 35-μm-thick outer layer,which matched the inner cube in composition,ensured that electronic equilibrium existed in the central dose-scoring cube.
The inner cube was made as large as feasible with available computer resources. The limiting factor in this was computer RAM,which needed to store information on a large number of MNPs distributed inside the inner cube with no overlap. Computational feasibility of the simulation was tested for the scenario that demanded the highestcomputer capacity,which is that of 10-nm nanoparticles at a metal concentration of 50 mg per 1 g of H2O, when the corresponding number of MNPs per unit volume inside the inner cube was greatest. The largest inner cube for which computer RAM did not overflow in this case had an edge length of 30 μm. To ensure that electron equilibrium existed both in the direction of incident gamma rays and laterally, the edge length of the outer cube was set at(35 + 30 + 35) μm = 100 μm.
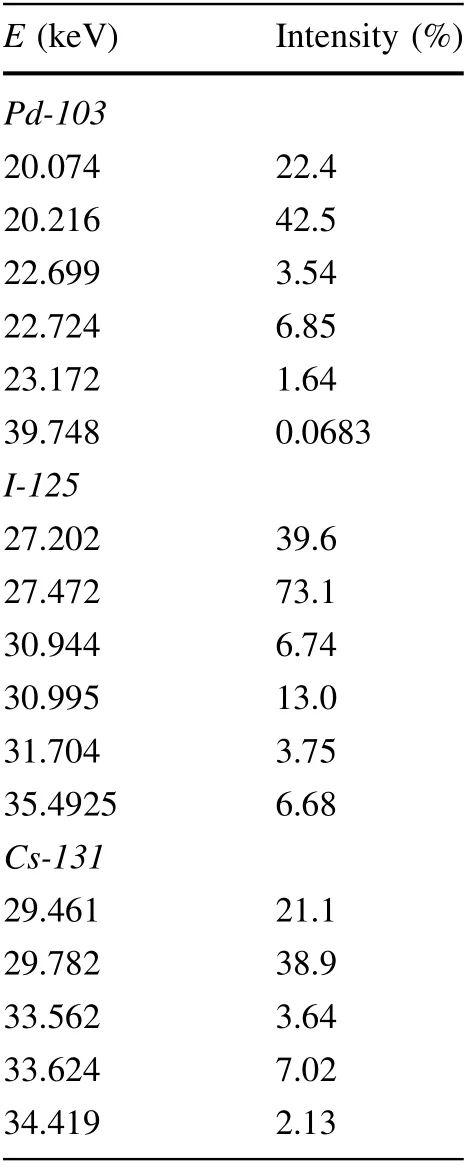
Table 1 Energies and relative intensities of gamma rays and characteristic X-rays from the three sources used in simulations [63]
For low concentrations(below 1 mg of metal per 1 g of H2O) and large NPs (diameters over 100 nm), the inner cube was made larger, so as to enhance the statistics of photon interactions when the number of MNPs per unit volume was low. The edge of the outer cube was in each case larger by 2 × 35 μm = 70 μm.Making sure that there were at least 103nanoparticles in the inner cube,the largest edge was 200 μm, for the case of 400-nm nanoparticles at 0.1 mg per 1 g of H2O. The edge length of the outer cube was then (35 + 200 + 35) μm = 270 μm. The upper bound on the nanoparticle diameter was set at 400 nm based on the typical size of pores in the tumor vasculature[64].
While spherical nanoparticles are distributed uniformly within the inner cube during the geometry space construction phase of the simulation run, they should not overlap one another or cross the cube faces.Because some combinations of nanoparticle concentration and size translate into several million MNPs in the inner cube, the built-in Geant4 C++ classes that can be used to achieve this would have demanded unrealistically long computation times on the computer platform used.A simple custom C++ code was therefore developed for nanoparticle placement according to the uniform distribution in 3D,which guaranteed that no two MNPs intersected and that none of them protruded from the cube. If the number of MNPs in the inner cube exceeded 150,000, the algorithm implemented in this code would divide the cubic volume into smaller rectangular parallelepipeds and ensure the nooverlap condition in each of these subvolumes separately,thereby significantly shortening computation times.
When compared to some previous investigations, the described geometrical model might be called heterogeneous, since it contains two subregions with different structures [51]. However, this term may be misleading, as one of the two subregions is indeed homogeneous,which is why a better-suited description would be multi-structural,or better still bi-structural. Two more common descriptors for some of the earlier models are multiscale (used to designate different physical models of radiation transport applied to different regions) and two-stage (when scaling of photon field phase space is performed between macroscopic and microscopic stages of the simulation)[47, 49, 51]. Neither of these terms is appropriate for the model in the present study,since physical models of photon and electron propagation are the same in both subregions(e.g., secondary electron transport is modeled by the condensed history approach throughout the whole volume),and simulation is conducted in a single run (or ‘‘stage’’).
2.3 Radiation sources
Three commonly employed brachytherapy sources were considered(Pd-103,I-125,and Cs-131),all of which decay almost exclusively through electron capture, followed by the emission of gamma and characteristic X-rays in the 20—40 keV range. The energies and relative intensities of gamma and X-rays from the three radionuclides used in the simulations are presented in Table 1. Some gamma and X-ray lines with relative intensities lower than 0.05%were neglected, as were the low energy lines that produce secondary electrons that cannot penetrate typical encasements of brachytherapy sources.
Photons from the source were incident uniformly and perpendicularly on one face of the outer cube(the left-hand face in Fig. 1). The photon field in the model was unidirectional, with a square cross section equal to the outer cube’s face, ranging from 100 μm × 100 μm to 270 μm × 270 μm in various runs. This simplified field geometry approximates a planar brachytherapy source directly adjacent to the treatment volume.
2.4 Choice and adjustment of physical models
Monte Carlo models for calculating radiation energy deposition at the micro-and nanoscale fall into one of two categories: track-structure (TS) and condensed history(CH) models. When used for analyzing radiotherapeutic techniques, the two categories differ primarily in the treatment of electron transport.
Track-structure codes simulate each electron interaction down to the energies of several electronvolts. In order to model electron transport in matter faithfully, with detail and precision, these codes require sizable quantities of input data that describe the materials through which electrons propagate. In addition to entailing time-consuming computations, the detailed representation of TS models is limited by the lack of precise data on cross-sections for various materials. At present, only two media for which such accurate data are available are water and gold[61, 65].
CH codes, on the other hand, typically follow electrons only down to approximately 1 keV and also lump (or condense) low-energy transfer events into steps, over which the effect that these events have on electron history and energy deposition in matter is averaged.The only input data needed are the energy loss per track length (i.e.,stopping powers), which are well known for all elements,and hence materials. The CH codes are superior with regard to computation speed and generality of application.Their main drawback is the spatial resolution limit, which is approximately 0.1 mm, while TS codes attain subnanometer resolution [35]. In order to improve the spatial resolution, some CH codes implement a ‘mixed’’approach, lumping soft collisions (i.e., those with low energy transfer) together into steps, and simulating hard collisions discretely by single-scattering cross sections.Setting the hard collision energy transfer threshold to zero should,in principle,enable mixed CH codes to simulate all collisions in a discrete manner, thus approximating a TS code [66]. Previous investigations have indicated that the Livermore physics model in Geant4 has gotten furthest along these lines [67—69]. The latest version of the G4EmLivermorePhysics constructor in Geant4 enables electron ionization and bremsstrahlung production to be followed down to the low energy limit of 10 eV, although the recommended applicability range is above a few hundred eV [70, 71].
The Geant4 toolkit contains both condensed history and track structure physical models of electron transport.However, none of the track structure models implemented in Geant4(version 10.5)have been developed for materials such as gold, silver, or platinum,but only for liquid water.For this reason,condensed history models were used in the present study. The three research papers cited earlier,which compared Geant4 CH models to TS models, were used as a basis for choosing an optimal physical model in the present investigation [66—68]. These previous investigations provided guidance on how to adjust simulation parameters,namely the secondary production cut,step-size limit,and lowest electron energy, to bring CH calculations closest to those performed with the TS approach. Of the various CH models, the aforementioned Livermore model proved to yield the best results in micro- and nanoscale electron transport and hence was the algorithm of choice herein. Production cut is the energy limit for a secondary particle at the instance of creation below which it is not propagated, but rather has its energy deposited locally at the site of creation.Step-size limit is the upper bound to the distance along which an electron is propagated with the CSDA energy loss. The propagation of an electron is terminated once its energy falls below the lowest electron energy value, with the energy it has at that moment deposited locally.
Using earlier investigations as guidelines, simulations for the present study were first run with adjustable parameters set at especially low values:production cut was set at 10 eV, step-size limit at 0.1 nm, and lowest electron energy at 1 eV. With parameters adopted at such strict levels, computation times turned out to be prohibitively long with the available computer platform. An optimal set of the three stated parameters was therefore looked for by varying one at a time,with the other two at fixed values.In addition to the tolerable duration of a simulation run,which was arbitrarily set to 24 h,another criterion for accepting a specific value for a parameter was the quality of the obtained results, as compared to the most stringent case with the same number of histories. A result was deemed acceptable if it deviated by less than 1% from the one obtained with all three parameters at the lowest applied values.Examination of simulation times and result validity for various MNP sizes and concentrations indicated that the Livermore model was very sensitive to changes in the production cut and lowest electron energy, in line with conclusions from [68], and consequently these parameters were kept at the initial stringent values of 10 eV and 1 eV,respectively. Variation in the step-size limit, on the other hand, had no observable influence on the result variability or uncertainty. No upper bound on the step size was therefore mposed, with the actual size of each particular step depending only on the physical and geometrical models. This relaxation of the step size limit, along with the restrictions regarding sizes of subregions in the geometrical model described in Sect. 2.2, provided a roughly 100-fold reduction in computation time compared to the initial 0.1 nm step size.
3 Results and discussion
The approach to DEF correction calculations applied herein was first tested and verified by comparing the results to those from two similar previous studies, which considered only gold nanoparticles [48, 51]. The correction coefficient was termed ‘‘dose ratio’’ in those papers. The comparison included two nanoparticle diameters (20 and 100 nm), three concentrations (5, 10, and 20 mg of gold per 1 g of ICRU tissue),and three photon energies(20,30,and 50 keV). While the present study utilized Geant4 for simulations, the two reference papers used PENELOPE and EGSnrc Monte Carlo packages, respectively. The corresponding results are presented in Table 2.
The values of the correction coefficient obtained in this study are close to the dose ratios from the two earlier studies. There is, however, an overall systematic deviation of the new correction coefficient values, in that they are to some extent higher than in the previous studies.This means that Dtand Dmixin Eq. (6) differ less, and a somewhat larger fraction of deposited energy is expected to reach the tissue surrounding the NPs than previously shown. The reason for this difference lies in the fact that in the present study, production of secondary electrons was allowed down to an energy of 10 eV, while in the two referenced papers this limit was higher (see discussion below). This difference in the production cut becomes notable for small nanoparticle diameters, since low-energy electrons, when allowed to propagate, have a chance of leaving the NPs,and for considered low nanoparticle concentrations hardly ever reach other NPs, but rather stop in the surrounding water/tissue. The regularity of the deviation in the new results is disrupted in a total of five cases, when the correction coefficient was found to be lower than in previous investigations. These five instances all occur for 50 keV photons, since at this energy of incident photons very-low-energy electrons contribute less to the total dose.
Precision of the Monte Carlo simulations was estimated according to the recommendations laid out in Chapter VI of the MCNP5 manual [73]. The number of histories was chosen so that the relative expanded uncertainty remained below 1% in all simulation runs.
The simulation results for the dependence of the DEF correction coefficient r on nanoparticle concentration and diameter are shown in Fig. 2 for gold,silver,and platinum NPs. From Eq. (6), it follows that lower values of the correction coefficient in these graphs denote a larger difference between DEF values calculated in the two previously described ways, with either a homogeneous or structured geometrical representation of the dose-scoring subregion.Because the calculated values of r are all below unity, DEFs obtained with the discrete representation of NPs (DEFstruct) are up to 49% lower than those calculated with the homogeneous mixture representation of the region(DEFmix). Part of the radiation energy deposited in the target region is absorbed in the nanoparticles themselves,and this energy is excluded from DEF when nanoparticles are modeled discretely. This phenomenon is ignored when the target region is treated as a homogeneous metal—water mixture,which leads to overestimated DEF values.Graphs from Fig. 2 are regrouped in Fig. 3 by joining graphs obtained for the same source and different metals.
The graphs in Figs. 2 and 3 demonstrate a general decrease in the correction coefficient r as either the concentration or size of nanoparticles increases, with some notable exceptions.For small nanoparticles,with diameters≤30 nm, r shows an initial decrease with concentration,but then tends to rise or level off as the nanoparticle concentration increases beyond 20 mg of metal per g of H2O.This tendency is visible in the upper right portions of the graphs in Fig. 3a,b,but even more clearly in Fig.4,where dependences of r on nanoparticle concentration are shown for 10 nm and 20 nm NPs, for all three sources. This observation suggests that when the concentration of small NPs rises, the deposition of photon energy within the nanoparticles is compensated by the increase in the total number of photon interactions and secondary electrons they produce.
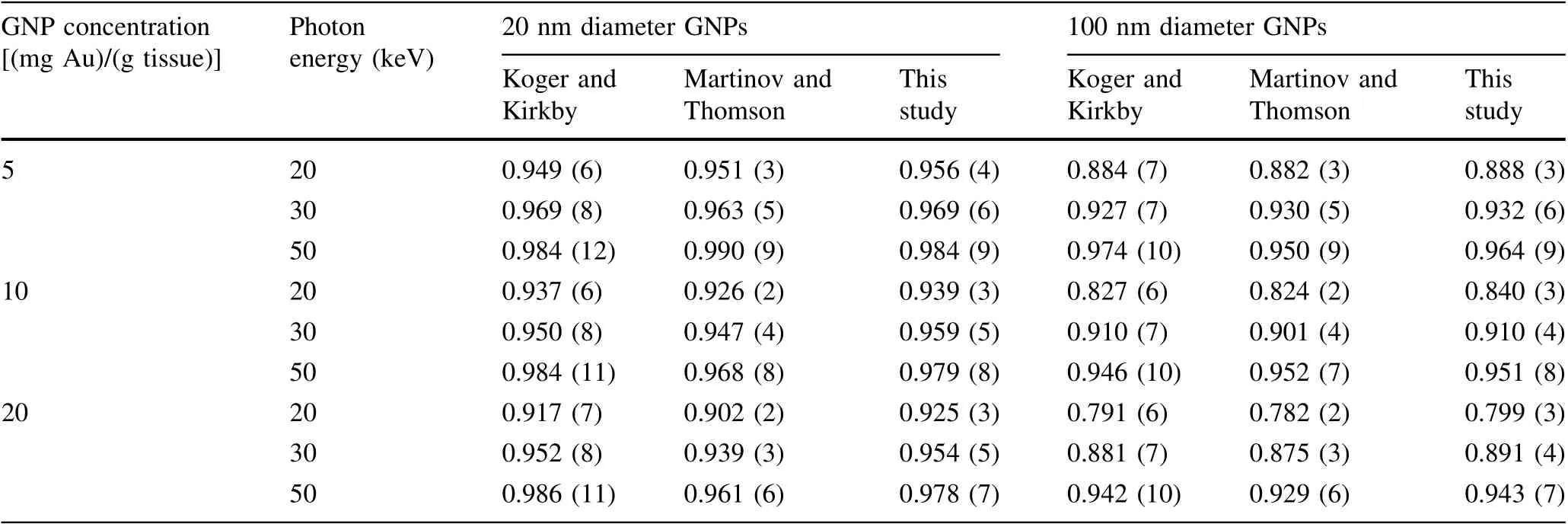
Table 2 Values of the correction coefficient r, calculated according to Eq. (6) for gold NPs in ICRU four-component tissue [72], compared to dose ratios found in independent studies by Koger and Kirkby [48] and Martinov and Thomson [51]
The least correction was observed for silver NPs and Pd-103 source. The corresponding graph in Fig.2b)shows that r stays close to unity for all concentrations and diameters of AgNPs.
By contrast,the same source led to the lowest values of r (i.e., greatest corrections) for gold and platinum NPs, as shown in Fig. 3c. The difference is caused by the position of the K-edge in the attenuation coefficient energy dependence relative to the gamma and X-ray lines of the palladium source (see Table 1). For the three investigated metals, the K-edge is at 80.7 keV for gold, 25.5 keV for silver, and 78.4 keV for platinum.
Another distinctive feature of the graph for AgNPs is that for smaller nanoparticles,greater correction is seen for the I-125 source than for Cs-131, while the opposite holds for larger NPs. This is shown more clearly in Fig. 5, in which the dependence of r on the silver nanoparticle diameter is presented for the concentration of 40 (mg Ag)/(g H2O).
Compared to previous studies in the same vein, the present paper offers several new perspectives and insights.Paper [54], for example, observed an overestimation of dose enhancement caused by the gold-water mixture approach, but concluded that values of DEF (calculated in MCNPX) for a given nanoparticle concentration either increased as the size of AuNPs increased, or were not considerably affected by it. The findings presented herein,however, show that the fraction of radiation energy that stays within discretely modeled NPs grows with nanoparticle size (see Fig. 4a), which is why DEF is expected to drop as AuNPs increase in size. This discrepancy can be attributed to differences in model geometry and limits in the physical models of particle transport.In[54],the dosescoring region (a cell nucleus) was void of NPs, which were present only in the volume surrounding it (cytoplasm), while in the present study discretely represented NPs are distributed uniformly throughout the scoring volume (see Fig. 1 and accompanying text). Moreover,MCNPX has a built-in electron energy cutoff of 1 keV,which is two orders of magnitude larger than the production cut used in the present study.
In [48], a cutoff energy of 100 eV was set for photon and electron production in PENELOPE, ten times the production cut adopted in the present investigation.Moreover, in that study, secondary electron equilibrium was initially modeled by transporting electrons leaving the region of interest back into it for full energy deposition,but then approximated by stopping the escaping electrons and depositing all of their residual energy in the tissue part of the region. The validity of this approximation may depend on nanoparticle concentration, which is why in the present study electronic equilibrium was established explicitly, by appropriately setting the composition and geometry of the outer cube surrounding the dose-scoring subregion, as described in Sect. 2.2.
In [51], photon and electron production was simulated using the EGSnrc Monte Carlo package down to an energy of 1 keV, compared to 10 eV used in simulations for the current study. That investigation used a tilted cubic lattice of AuNPs, as opposed to the computationally more demanding uniform distribution of NPs used herein.
These three and most of the other earlier papers that utilized a structured representation of the region loaded with nanoparticles investigated only gold nanoparticles[41—49, 51—54], while the present study offers a comparison of DEF corrections for three nanoparticle types. The results in Fig. 2 suggest that the difference between two representations of the target region (homogeneous and structured) affects the dose enhancement most when the Pd-103 source is used on gold or platinum NPs. For silver NPs, the difference is most pronounced when either the Cs-131 or I-125 source is used, depending on the nanoparticle size.
An approximate method for determining the correction coefficient r can be proposed, which would further speed up calculations, albeit with limited applicability constrained by nanoparticle size and concentration.If the mean energy imparted to the metal/tissue mixture is approximated by Emix≈Et+ Enp, Eq. (6) becomes:
and the need for running separate simulations with the inner cube filled by the water/metal mixture is obviated.Since each simulation run with a structured inner cube yields values of both Etand Enp,it also directly produces a value of the correction coefficient through Eq. (7). To test the validity of this approximation, values of r obtained from Eqs. (6) and (7) were compared for the range of nanoparticle sizes and concentrations used previously.Values obtained from Eq. (7) turned out to be higher, but only up to 1% in most cases, except for larger NPs, where greater deviations appeared, reaching 4% for Au and Pt nanoparticles with 400 nm diameters at maximum investigated concentration of 50 (mg metal)/(g tissue). In general, the approximation could be acceptable for diameters up to 100 nm and concentrations not greater than 30 (mg metal)/(g tissue).
4 Conclusion
Values of the dose enhancement factor in metal nanoparticle-enhanced photon brachytherapy, obtained from Monte Carlo simulations, were corrected for the fact that part of the deposited radiation energy stays in the nanoparticles themselves, never reaching their surroundings, and therefore does not contribute to therapeutically relevant dose. The correction was accomplished by modeling metal nanoparticles as discrete spheres distributed inside a target volume of water,instead of representing this region as a homogeneous mixture of metal and water.Three metals (Au, Ag, and Pt) and three sources (Pd-103,I-125, and Cs-131) were considered.
Several issues had to be solved to achieve this.The goal was to consider as many NPs as possible and make the structured subregion in the simulation geometrical model large enough to contain them. However, large numbers of NPs in the dose-scoring cubic subregion put high demands on computer system resources.The number of NPs and the size of this region had to be restricted so as to allow even the most demanding scenario—that of the smallest investigated nanoparticles at the highest investigated metal concentration—to be computed with the available hardware platform. Further partitioning of the structured volume was needed at high concentrations to facilitate computationally efficient nanoparticle placement without overlap or protrusion.
Electronic equilibrium was ensured in the central cubic subregion by enveloping it by a larger homogeneous cube with matching composition, the size of which was established based on the range of most energetic secondary electrons that appear for the three considered radioactive sources.
The investigation presented in this paper demonstrates that calculation of nanoscale dose deposition in NP-enhanced radiotherapy requires that particular attention be given to the relationship between the geometrical properties of discretely represented MNPs (their size, concentration,and distribution)and crucial parameters in physical models of secondary radiation emission and propagation.If presently available CH-based Monte Carlo simulations are used for secondary electron transport, the bounds of the simulation models need to be fine-tuned to arrive at accurate dose estimates. In the Geant4 Monte Carlo package used in this study, this refers to the secondary production cut,step-size limit,and lowest electron energy,which need to be adjusted so that the simulation comes as close to actual event-by-event tracking as practically feasible. The influence of these parameters was examined in the present study, which led to a stringent set of values for the parameters being adopted, allowing more precise determination of DEF corrections than in previous similar investigations.
The results obtained from these well-tuned simulations show that the correction coefficient r = DEFstruct/DEFmix,calculated for the dose-scoring subregion, is below unity for all MNP sizes and concentrations. This confirms that DEF is overestimated when the region is represented as a homogeneous metal—tissue mixture,because the part of the deposited radiation energy absorbed in the nanoparticles themselves is ignored.The fraction of deposited energy lost to nanoparticles generally increases as either the concentration or size of MNPs increases, resulting in a general decrease in r. Some notable exceptions to this trend are observed,such as for small NPs,for which r first drops,but then rises at higher nanoparticle concentrations, when photon energy deposited within the NPs is compensated by the increase in the total number of photon interactions and secondary electrons produced. For small AgNPs, greater correction is seen for the I-125 source than for Cs-131,while the opposite holds for larger NPs. The least correction overall(with r values close to unity)was observed for AgNPs and Pd-103 source, while the greatest correction(with lowest values of r) was found for Au and Pt nanoparticles when Pd-103 was used as a source.
The DEF correction demonstrated herein does not consider the biological effectiveness of deposited radiation energy,but only corrects the value of dose deposited in the biological medium (i.e., outside the MNPs), which can potentially contribute to the damage of targeted cellular moieties. Moreover, because only brachytherapy sources are considered, emitted photons are represented as immediately entering the target volume, with no previous alteration of the beam. The variation of DEF and its correction with depth in tissue will be investigated in a forthcoming study,which will include beam modification,and will then also apply to other types of photon radiotherapy.
Event-by-event models of secondary charged particle interactions and detailed physical models of relaxation processes in metals are needed to obtain simulation-based DEF estimations accurate enough to form reliable grounds on which to found future in vivo tests of metal nanoparticle-enhanced radiotherapy in human subjects. Once these TS models become available, Monte Carlo calculations will be able to deliver the correction coefficient r with even higher precision.
 Nuclear Science and Techniques2020年11期
Nuclear Science and Techniques2020年11期
- Nuclear Science and Techniques的其它文章
- Analytic RF design of a linear accelerator with a SLED-I type RF pulse compressor
- Preliminary analysis of fuel cycle performance for a small modular heavy water-moderated thorium molten salt reactor
- Effective (kinetic freeze-out) temperature, transverse flow velocity, and kinetic freeze-out volume in high energy collisions
- Design, assembly, and pre-commissioning of cryostat for 3W1 superconducting wiggler magnet
- Preliminary evaluation of the radiotherapeutic efficacy of 131I-atorvastatin in rats with hepatocellular carcinoma
- Design of a 162.5 MHz continuous-wave normal-conducting radiofrequency electron gun
