基于模型的车辆队列专用短程通信系统关键性能指标描述方法*

石 佳，罗禹贡，齐蕴龙，李克强

(清华大学车辆与运载学院，汽车安全与节能国家重点实验室，北京 100084)

前言

车辆网联化旨在通过无线通信技术实现车与车、车与路和车与人之间的信息交互，其不仅能提升车辆的感知和决策性能，还能有效地改善道路拥堵、降低污染排放、提升交通安全性[1]。 车辆队列是网联化的重要应用场景之一，同一车道内相邻车辆组成一个队列，通过调整车速保持期望的车距，从而降低燃油消耗率并提高交通效率[2-3]。 但是考虑到车辆的快速移动和行驶场景的复杂性，车与车通信节点形成的车载自组网(vehicular Ad-hoc network，VANET)[4]比节点相对静止时建立的移动自组网(mobile Ad-hoc network，MANET)更为复杂，通信过程中存在不可避免的时延和丢包问题，这对于智能网联车辆的控制有着重要的影响[5]。 要实现对车辆队列的精确控制，就须针对队列应用场景对通信系统的性能进行建模描述。

对于车辆网联下无线接入技术的选择，国际上主要形成了DSRC(专用短程通信)和LTE-V 两条技术路线，二者各有优劣[6]。 DSRC 主要基于IEEE802.11p 协议，采用了正交频分复用技术，发展较为成熟；LTE-V 基于移动蜂窝技术，有集中式和分布式两种工作场景，目前正在向5G-V2X 平滑过渡。 DSRC 与分布式的LTE-V 都是无线信号在通信节点间的“直连”，尽管二者在物理层和数据链路层的特点有所不同，但在车辆队列应用层中有诸多共性之处。

在目前的车辆队列研究中，通信性能是车辆队列控制必须考虑的因素。 秦晓辉等[7]针对通信时延的不确定性，提出了考虑时延下的车辆队列分布式控制器；Lei 等[8]研究了丢包率、发包频率和车头时距对队列弦稳定性的影响，并在交通和网络联合仿真软件中进行了探讨；Zeng 等[9]针对时延和丢包率等通信性能指标对队列控制器进行了设计和优化。此类研究大多从控制器设计出发，将时延和丢包率简化为带有边界的随机值[10-11]，研究其对系统稳定性的影响。 但这种简化没有考虑到实际通信特性，会对队列的控制性能造成影响。

通信领域的学者也对这一问题进行了研究，更多聚焦在信号能量、编码策略、转发特性等方面。 当网联车辆间进行无线通信时，信号的能量随着传播距离增大不断衰减，学者们考虑路径损耗、反射、散射等因素提出了大尺度衰落模型[12]和小衰落模型[13-14]。 考虑到视距传播内障碍物的遮挡，Sommer等[15]还探讨了障碍物遮挡特性与信号接收强度的关系。 但此类研究大多关注传输过程中信号能量的变化，没有针对车辆队列这一特定场景，探讨时延和丢包率等性能参数的变化规律。 此外，还有学者结合交通和网络仿真软件[16-18]对车联网相关场景下的通信性能进行了探讨，但大多都仅对仿真结果进行解释。

本文中从信号传输特性出发，基于无线信号传输过程中的通信延迟概率和功率强度分布特点，同时考虑道路环境、障碍物遮挡等因素的影响，建立了基于模型的车辆队列通信系统的通信性能指标描述方法，并设计了基于专用短程通信技术的多车通信试验，进行了模型参数标定与验证。 该模型考虑了队列场景的特点和车辆自身特性，可用于车辆队列控制中。

1 通信性能指标模型描述

车辆队列通常由头车与多辆跟随车组成，通过车车通信共享信息，从而实现队列协同行驶。 通信拓扑结构反映了信息在车辆队列间的传输关系，通常有“前车跟随式”“双向跟随式”“前车-头车跟随式”和“双向-头车跟随式”等多种形式。 受通信技术特性的限制，信息在车间传输的过程中存在时延和数据包丢失现象，这将影响网联车辆控制器性能，进而造成队列行驶过程中的安全性隐患。

本文中研究的车辆队列通信拓扑关系如图1 所示，其中节点A 为头车，其余节点为跟随车，所有节点车辆均为网联车辆。 对于节点A 发送信号被节点F 接收的过程，信号可以通过“单跳”的方式从节点A 直接传播到节点F；也可以先传播到中继节点B，再由节点B 进行“双跳”转发到节点F；还可通过多个中继节点的“多跳”转发实现。 不同信号在源节点A 和目标节点F 之间传播所选择的路径相互独立，选择每条路径的概率也互不相同。 本文中将选取端到端时延和丢包率两个主要通信性能指标，对队列通信系统性能进行建模描述。

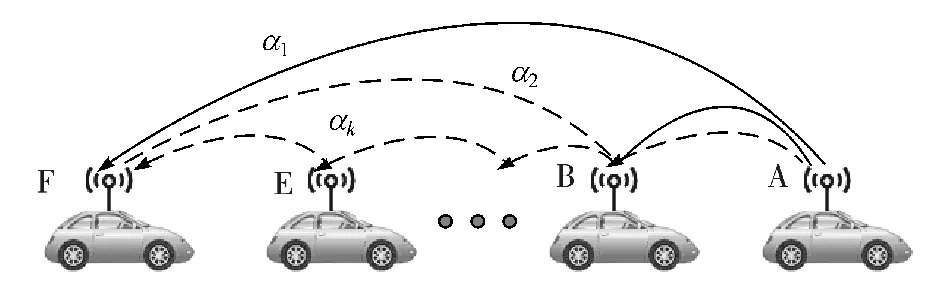
图1 车辆队列通信拓扑关系图

1.1 端到端时延模型

端到端时延(end-to-end delay)是指信号从源节点发出到被目标节点接收所需要的时间。 对于A 到B 单跳过程，单跳总时延t1，tot由两部分组成，其一为源节点申请并获得访问信道媒介资格所需要的时间，记为τa，另一为信号从源节点发出后，在信道空间中传播到达目标节点所需要的时间，记为τab，则总时延可表示为

对于一个随机的无线通信过程，假设每一次通信过程随机且独立，单跳总时延的概率密度函数f1，tot(t1，tot)为

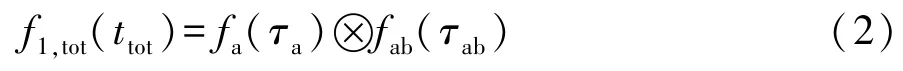
式中fa(τa)、fab(τab)分别为随机变量τa、τab的概率密度函数，f1，tot(t1，tot)为二者的卷积，表示t1，tot的概率密度函数。 根据无线网络通信延迟概率分布特点，可将τab近似为一常数[19]。 引入δ(Dirac)函数对卷积进行化简:

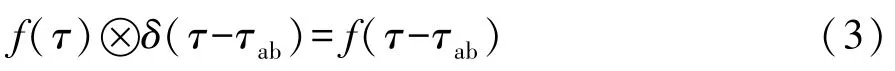
这意味着对于概率密度与δ函数的卷积计算只须将概率密度沿横轴移动一常数即可，根据δ函数的性质，t1，tot的概率密度函数可表示为

fa，pat(·)与fa(τa)有相同的形式，其含义为单跳总时延的概率分布。 对于节点A 通过多个节点转发到达节点F 的“k跳”过程，记信号在第i个节点中进行处理的时间为τi、信号从第i个节点发出在信号空间中传播并达到第j个节点的时间为τij，则“k跳”过程总时延tk，tot为

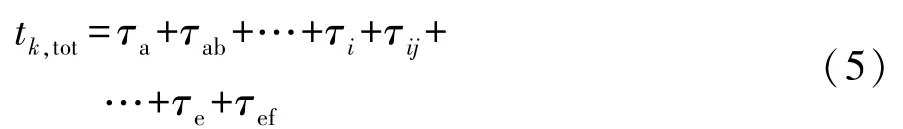
根据式(3)和式(4)可知，“k跳”过程总时延tk，tot的概率密度函数为

本文中采用三参数Burr 分布来描述“k跳”过程总时延的概率分布，其概率密度函数为

式中:α为尺度参数；β、γ为形状参数。 对于从节点A 到节点F 的通信过程，记通过第i跳路径到达的信息占总体信息的比例为ai，则端到端总时延的概率分布可表示为

1.2 丢包率模型

丢包率(packet error ratio， PER)是指通信过程中丢失数据包数量与发送数据包总数量的比值，反映了通信过程的质量和可靠程度。 造成数据包丢失的原因很多，包括设备故障、物理线路故障、信道衰落、路由错误和网络堵塞等，其也会受到信号收发特性的影响。

对于无线通信而言，造成丢包最主要的因素为信号在信道空间传播过程中功率强度的降低，当其低于功率强度阈值时，就无法被目标节点接收。 因为多径效应的存在，某一位置处接收到的信号其实是大量直射信号、反射信号等的叠加，其功率强度满足一定的概率分布规律。 Taliwal 等[20]的研究表明，Nakagami-m 分布能很好地描述无干扰情况下信号在空间信道中传播的功率强度概率分布规律。 根据Nakagami-m 分布，在通信距离为d处的接收信号功率强度的概率密度函数(PDF)fd(x；m，Ω)为

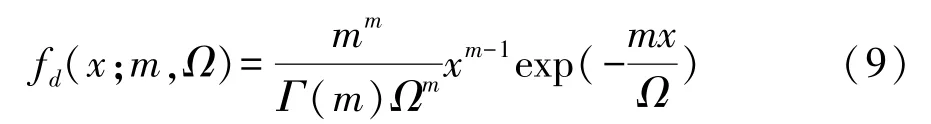
式中:m为信道衰落参数，m越大表示信号衰减越慢、信道质量越好，当m趋近于正无穷时表示信道无衰落；Ω为平均功率强度，Ω越大表示信号传播距离越远；Γ(m) 为伽马函数。 通信距离为d处的接收信号功率强度的累积密度函数(CDF)Fd(x；m，Ω) 为

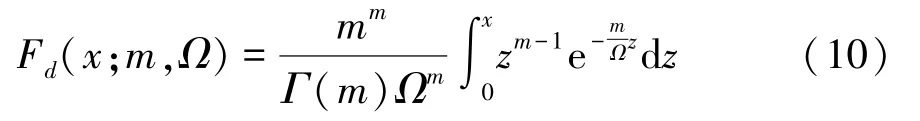
结合Gamma 分布Γ(b，p) 的累计密度函数公式和 Erlang 分布规律，并令b ＝m/Ω，p ＝m，可将式(10)化为

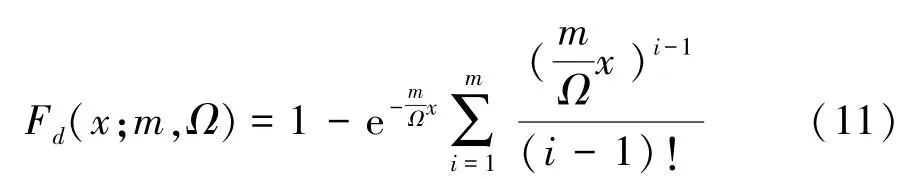
假设接收功率强度阈值为Rthre，高于该功率强度阈值的信号能被接收，则收包率可表示为

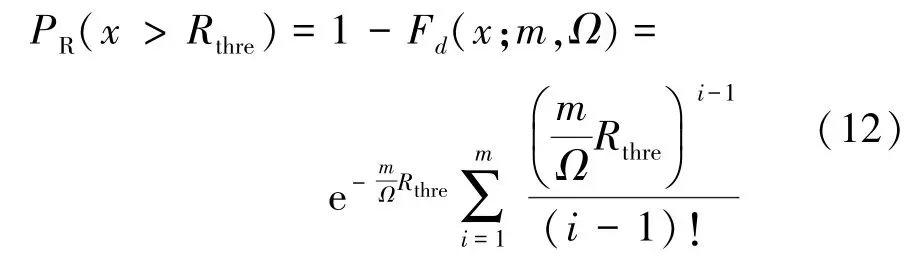
信号在不同的信道空间中传播对应了不同的信道衰落系数。 在本文的推导中，取m ＝3，则收包率可表示为

根据Ferris 自由空间路径损耗模型，可以得到接收功率强度阈值Rthre和平均接收功率Ω(d) 的表达式为

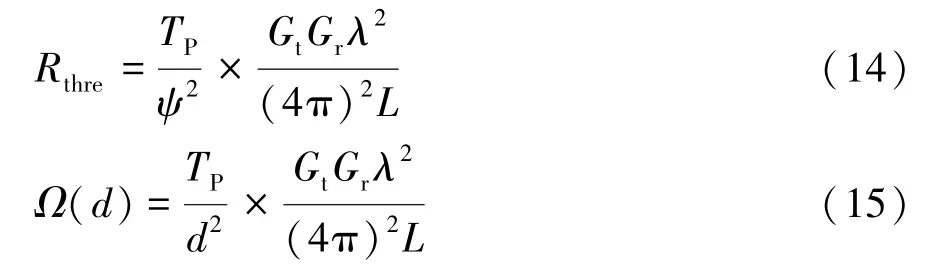
式中:TP为所选择的传输功率；ψ为传输特性参数；Gt、Gr分别为发送天线增益、接收天线增益；λ为传播波长；L为路径损耗系数。 将式(14)和式(15)代入式(13)，得

式(16)为仅考虑沿途路径损耗推导出的收包率模型，其中收包率只与通信距离和传输特性参数有关，并且具有相似的变化规律。 传输特性参数ψ综合反映了通信信道的质量，不同传输特性参数下的丢包率变化如图2 所示。

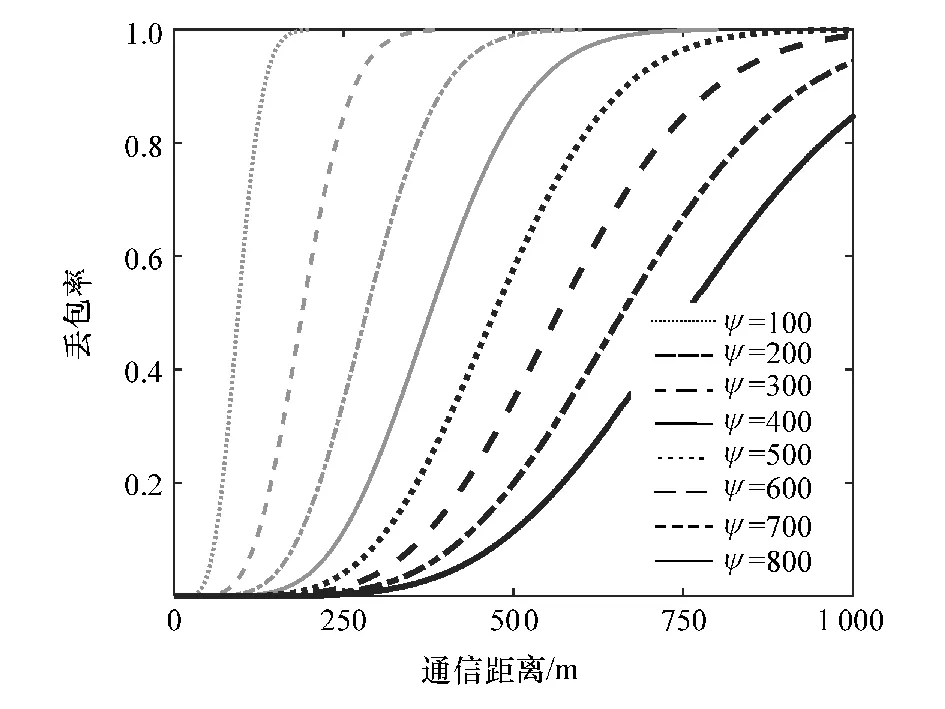
图2 不同传输特性参数ψ 下的丢包率变化

除沿途路径损耗之外，视距传播内的障碍物遮挡(如其它车辆、行人以及道路不平度)也会影响通信性能。 假设位于源节点前方di处的第i个障碍物对于di ～(di ＋Δdi) 范围内的通信性能有影响，其对丢包率的影响峰值为kdikbiC，其中kdi为第i个障碍物与源节点之间的距离影响因子，kbi为第i个障碍物形状、大小影响因子，Δdi也受障碍物形状大小的影响，则由于第i个障碍物造成的额外收包率损失Ploss，i为

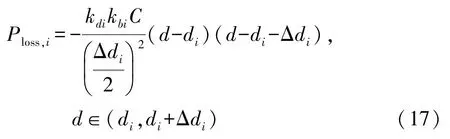
考虑视距传播内所有障碍物的遮挡，则修正后的收包率PR，modi为

多跳过程的收包率PR，multi近似等效为多个单跳过程收包率PR，i的乘积，如式(19) 所示。 其中，PR，i表示第i个过程的收包率。

2 队列通信系统搭建

2.1 队列通信系统硬件平台

队列通信系统由头车、跟随车1、跟随车2 组成，如图3 所示，其中头车由人驾驶，并负责发出组队和避障信号，跟随车为自动驾驶车辆。

图3 队列通信系统

网联车辆以长安CS55 为基础进行改装，其平台架构如图4 所示。 车辆的转向、油门和制动均已改为线控方式。 定位系统采用联适差分GPS 设备，车辆能够获取厘米级的高精度定位信息，该系统也能实时提供车辆的速度、加速度、航向角等状态信息。 车辆队列间采用星云互联OMI 设备作为无线通信设备，其可同时支持DSRC 和LTE-V 两种方式。 轮速传感器采集到的车速信号、定位系统获取的定位信号、车辆控制器发出控制和反馈信号都先发送到CAN 总线，通信设备从CAN 总线获取信号进行广播，并将接收到的可用信号写入CAN总线。 采用dSPACE 作为整车控制器，在上位机中使用ControlDesk 可实现数据的可视化显示及实时调试。

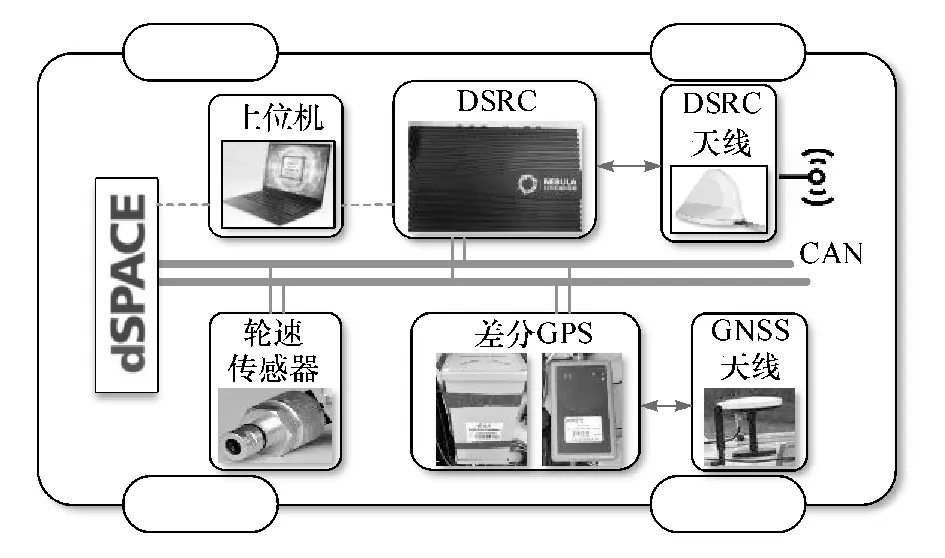
图4 网联车辆平台架构

2.2 队列通信协议

在车辆队列应用中，每辆网联车都将周期性广播通过自身传感器获得的位置、速度和加速度等信息。 头车还须额外广播控制指令，以实现组队、避障等功能，跟随车在收到前车控制指令后须反馈自身状态信号，本研究中制定的通信协议如表1所示。

表1 通信协议

队列中采用“前车-头车跟随模式”，对于每一辆跟随车，都可接收到来自前车与头车的信号，以实现自车的轨迹规划和运动决策。 当头车与跟随车的距离较远时，头车控制信号可能无法直接传到跟随车辆，此时需要其余车辆作为中继节点进行转发。信息来源的识别通过判别数据包中的设备号和车辆类型确定。

2.3 队列通信系统软件平台

通信系统软件平台基于C＋＋开发，其架构如图5 所示，主要包括预配置和3 个核心线程。

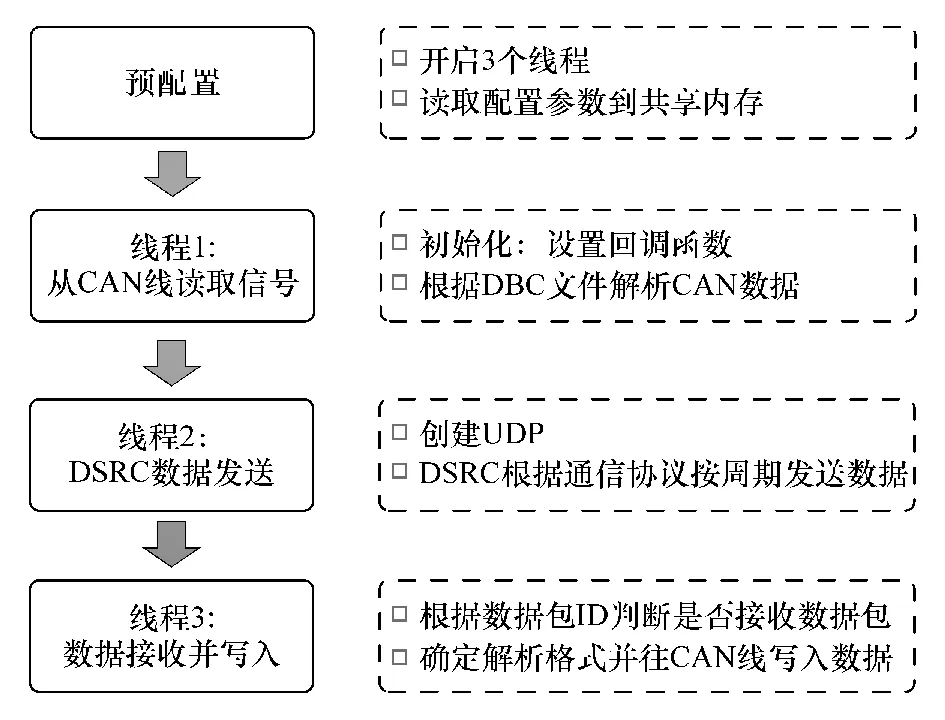
图5 通信系统软件架构

在预配置环节开启3 个核心线程，并将发送频率、发送模式、车辆类型等参数从配置文件中读取到共享内存，便于程序调用。 线程1 的功能主要是根据DBC 协议对CAN 总线中的数据进行解析，获取需要传输的目标参数值。 线程 2 主要负责创建UDP，建立多台通信设备间的联系，并根据通信协议按周期发送数据。 DSRC 为广播模式，在信道空间通畅的情况下，DSRC 设备可以接受到空间中所有的数据包。 线程3 会根据数据包ID 值判断其来源并决定是否对其进行解析，之后按照解析格式往CAN 线写入数据。

2.4 通信性能指标

通信系统主要考虑通信距离、端到端时延、丢包率3 个性能指标，它们都可在上位机和终端交互APP 中实时显示。 通信距离根据两节点间的GPS坐标计算求得，假设A、B两节点的GPS 坐标分别为A(lonA，latA) 、B(lonB，latB) ，则两节点之间的距离dAB为

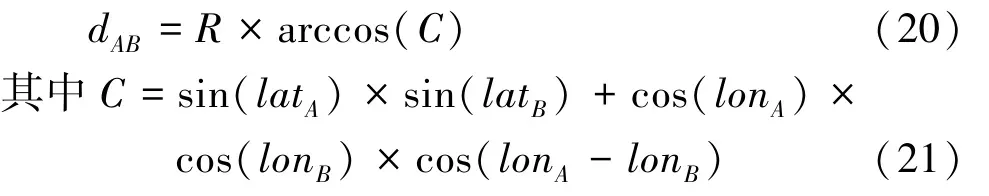
式中:R为地球半径，取6 371.004 km；C为变量。

端到端时延可通过信号被接收的时间戳和信号发送的时间戳作差计算得到，但由于两通信设备内部时钟存在固有时间差，所以需要对设备时间进行同步。 记A 设备向B 设备发送信号的时间戳为T1，B 设备接收到信号的时间戳为T2；同时记B 设备向A 设备发送信号的时间戳为T3，A 设备收到信号的时间戳为T4。 假设两个过程的时延相同，则两设备之间的固有时间差Δt为

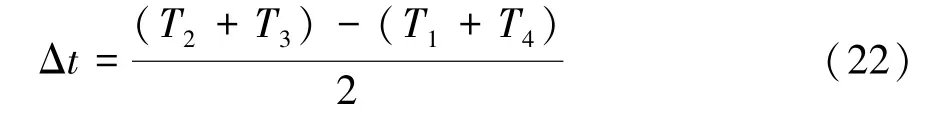
源设备发出的每个数据包都有唯一的ID 号，目标设备在接收端通过检测ID 号判断数据包是否丢失或者顺序错乱。 对于通信过程s，丢包率的计算公式为

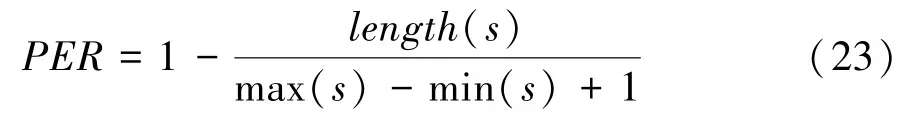
式中:max(s)、min(s) 分别为s过程消息的最大、最小序列号；length(s) 为s过程接收到的数据包数量总和。

3 通信性能测试试验与模型验证

3.1 通信性能测试试验

车辆队列主要应用场景为高速公路工况，但同样可适用于交通场景较为复杂的城市工况中。 基于队列通信系统，进行了通信性能测试实现，并通过测试试验结果对通信模型进行验证。 测试试验主要包括直线道路、十字路口和复杂城市道路3 种场景，试验在清华大学和重庆西部汽车试验场中开展，在前者中进行城市道路直线、十字路口、复杂道路工况试验，在后者中进行高速道路直线工况试验，测试场地如图6 所示。

图6 通信性能测试场地

在不同工况的直线道路场景中，跟随车以一定速度从超出通信范围(800 m)外接近头车。 该测试主要探究在不同沿途路径损耗系数对应的工况下，队列间丢包率与相对通信距离之间的关系，以及丢包率受视距传播范围内障碍物遮挡的影响。

在十字路口场景中，头车与跟随车分别在十字路口两条直角边行驶，设置十字路口有无中继节点转发两个工况进行对照。 该测试主要探究在有无中继节点进行转发条件下，单跳和多跳过程对于队列间丢包率的影响，同时探究单跳和多跳过程端到端时延的分布规律。

在复杂城市道路场景中，头车和跟随车以10 ～30 km/h 的速度行驶，并保证两车间距在20 ～250 m之间，该测试主要探究在十字路口、直角弯道、沿途障碍物遮挡、视距传播障碍物遮挡的综合道路下的队列通信性能特点。

3.2 通信模型验证

根据端到端时延模型，多跳过程时延呈现多峰分布，每个峰所占的比例与通信环境有关；并且每个单峰服从Burr 分布。 图7 为端到端时延模型验证结果，其中柱状图为实际统计量，曲线为根据时延模型标定后的概率分布，标定结果如表2 所示。 对于图7(b)和图7(c)两个双跳过程，在图7(b)中队列间头车与跟随车间距离较小，通过单跳过程进行通信的概率更大，在图7(c)中队列间头车与跟随车间距离较大，更多的节点通过两跳的方式实现通信。在所有通信过程中，单峰都能很好地服从Burr分布。

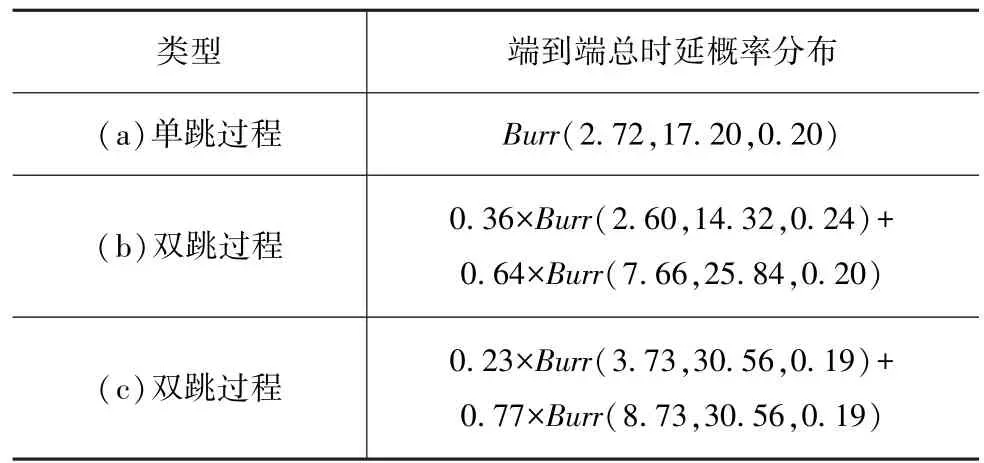
表2 端到端时延模型

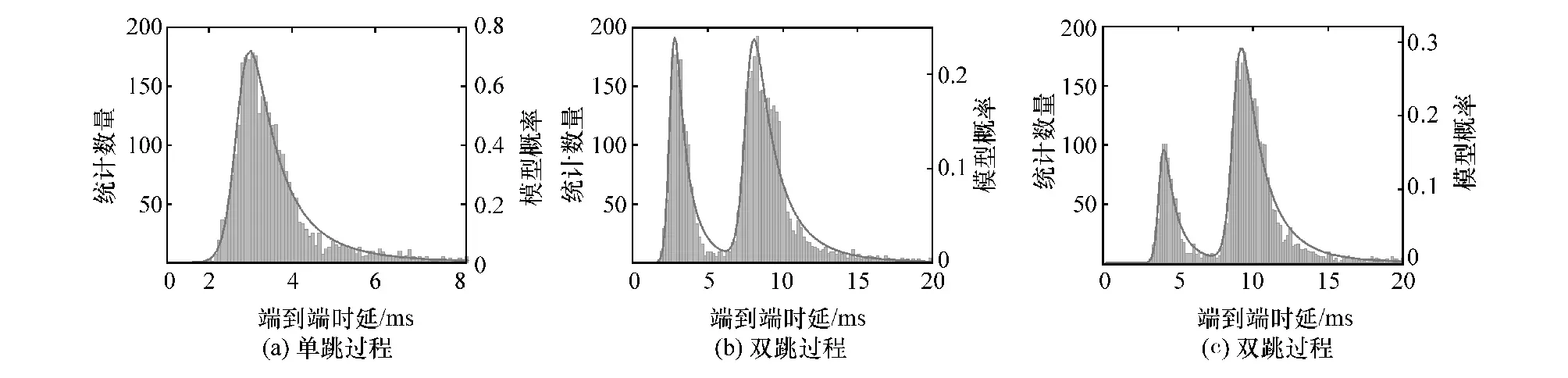
图7 端到端时延模型验证

根据丢包率模型，在无等效障碍物遮挡情况下，丢包率与通信距离间呈正相关关系，受视距范围内等效障碍物的影响。 图8 为丢包率模型验证结果，其中虚线为实际测量值，实线为根据丢包率模型标定后的变化趋势，标定结果如表3 所示。 图8(a)和图8(b)为只有沿途路径衰落且无视距传播内等效障碍物遮挡的场景，对应丢包率曲线光滑；图8(c)和图8(d)为视距传播内有一个等效障碍物遮挡的场景，对应丢包率曲线有一个凸峰；图8(e)和图8(f)为视距传播内有两个等效障碍物遮挡的场景，对应丢包率曲线有两个凸峰。 结合场景特点和标定结果可以说明:通信场景的复杂程度直接影响了传输特性参数，在树木、建筑物较少的开阔场景中，传输特性参数较大，因此通信性能较好；而在树木、建筑物较为密集的复杂场景中，传输特性参数较小，通信性能相对较差；同时，等效障碍物造成了局部收包率的损失，不同等效障碍物导致的影响范围和影响幅度有所不同。

图8 丢包率模型验证

表3 丢包率模型参数标定

3.3 通信性能测试试验结果分析

图9 为直线道路场景中不同工况下队列间丢包率与通信距离的关系，图中的点为一段时间内平均通信距离对应的平均丢包率，曲线为丢包率拟合的结果。 工况1～工况3 为城市道路，道路两侧有较高建筑物和树木，道路中存在其它车辆和交通参与者，ψ值较小；工况4 和工况5 为高速道路，道路两侧障碍物较少，空间比较开阔，ψ值较大。 试验结果表明，所有工况都能在一定距离内保持较低的丢包率，且丢包率在宏观上呈现出与通信距离正相关关系。在传输特性参数ψ较小的城市道路中，通信距离较短，丢包率在通信距离超过200 m 后迅速增加；在ψ较大的高速道路中，系统可在500 m 内维持较好的通信性能，丢包率在500 m 后随通信距离增加。 此外，受视距传播范围内障碍物和道路不平度的遮挡，会在局部距离区间内产生较高的丢包率，丢包率影响呈现凸峰特性，这对通信性能的影响较为严重。

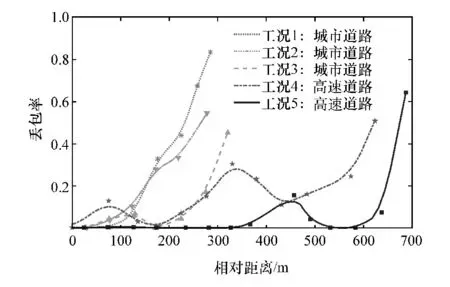
图9 直线道路丢包率测试结果

图10(a)和图10(b)分别为无、有中继节点下十字路口场景中队列间丢包率的测试结果。 试验结果表明，对于无中继节点的单跳过程，车辆的通信距离不会超过30 m；而当有中继节点进行转发时，跟随车可与150 m 外的头车通信，这极大地提升了队列的可通信长度，扩展了应用范围。

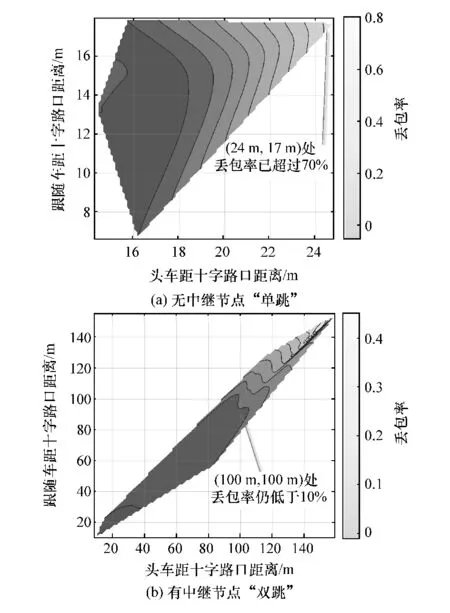
图10 十字路口丢包率测试结果

图11 综合反映了复杂城市道路场景中的队列间丢包率特点，经纬度确定了头车的运动轨迹。 在空间开阔且只有少量车辆、行人遮挡的直线道路中，丢包率能保持较低的值；在交通状况比较复杂的十字路口，最大丢包率可达到40%；在较高树木遮挡且通信距离大于200 m 时，最大丢包率超过60%；在无中继节点的直角转弯处，由于大型建筑物的遮挡，甚至会出现信号完全丢失，不能通信的现象。

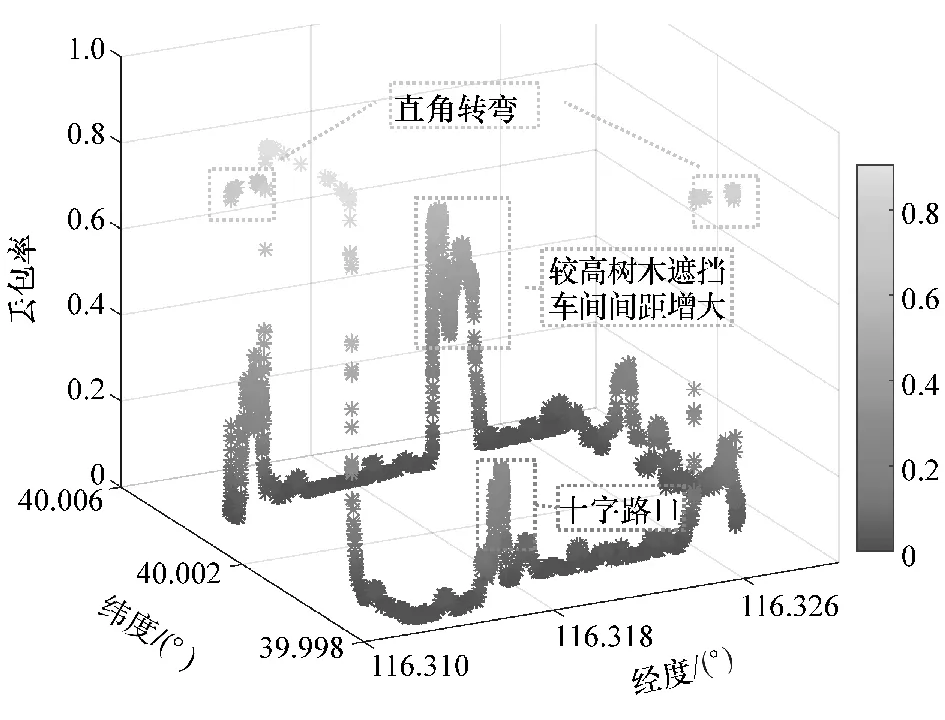
图11 复杂城市道路丢包率测试结果

表4 给出了不同场景中端到端时延的测试结果，可以发现端到端时延的平均值在低速的城市道路中稍高于其在速度较高的高速道路的平均值，但是二者相差不会很大，双跳时延的平均值为单跳时延平均值的两倍多。 结合图12 和图13 进一步说明，时延并不为一个定值，而是呈现出一定概率分布的规律。

表4 端到端时延测试结果

图12 单跳过程端到端时延测试结果

4 结论

本文中根据无线网络通信延迟和无线信号功率强度的概率分布特点，并考虑到车辆队列中障碍物遮挡的特点，建立以丢包率和端到端时延为指标的可用于队列通信系统的基于模型的通信性能描述方法。 基于所搭建的多车通信平台，进行典型工况下的实车试验，验证了所提出模型的正确性，主要结论如下。

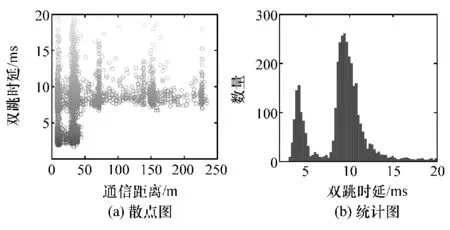
图13 双跳过程端到端时延测试结果

(1)丢包率与通信距离呈正相关关系，传输特性参数反映了环境特点，决定了丢包率的变化速率，视距传播内障碍物遮挡对局部丢包率有严重的影响。

(2)有中继节点的多跳过程能降低丢包率，扩大队列的通信范围。 当队列长度较大或者队列经过有障碍物遮挡的十字路口时，可将中间车辆或路侧单元作为中继节点，从而大幅度提高通信性能。

(3)多跳过程的时延呈现多峰分布的特征，每个峰所占的比例取决于通信环境，当通信距离较远时，多跳部分所占比例比单跳部分更高，每个单峰都可用Burr 分布进行刻画。