一图多变,认识小数有梯度
安夏月

【摘要】在小学数学的学习过程中,将数学概念转化为形象的图形,有助于将数学问题简单化和直观化,便于学生理解和掌握。小学数学教材中,直观图的呈现有很多,如何选好、用好并将直观图用到位非常重要。本文将以《小数的初步认识》为例,具体谈谈如何借助直观图进行小数概念的教学。
【关键词】直观图 多变 认识小数
《义务教育数学课程标准(2011年版)》强调,“重视学生已有的经验,使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程”。因此,教师在教学“小数的初步认识”时,不应把小数当作一个抽象的“数”,而应结合学生生活中有经验的“量”和具体的直观模型进行教学。
建立小数的概念,首先是为了满足现实世界中数量表达的需要,比如7元5角就可以表示为7.5元。小数的初步认识,要在认识整数十进位值制和初步认识分数的基础上,借助具体的量(米、分米、厘米;元、角、分)和几何直观图,直观感受小数与十进分数之间的关系,初步认识小数。
苏教版数学教材是通过以上两个例题来分别教学零点几和几点几的。相对于长度单位,学生对人民币的使用有更多的经验,通过货币单位元、角、分的十进制关系让学生直观感悟小数也是一种对数量关系的表达,可以让学生对“十进制”的感触更深。为了让整个教学更加直观系统地呈现给学生,笔者将教材中的例1进行了修改,以“元、角、分”的认识引入,逐步转化为直观图的变化,以图形的延伸贯穿整个教学设计。
一、实物图,从身边的事物来引入
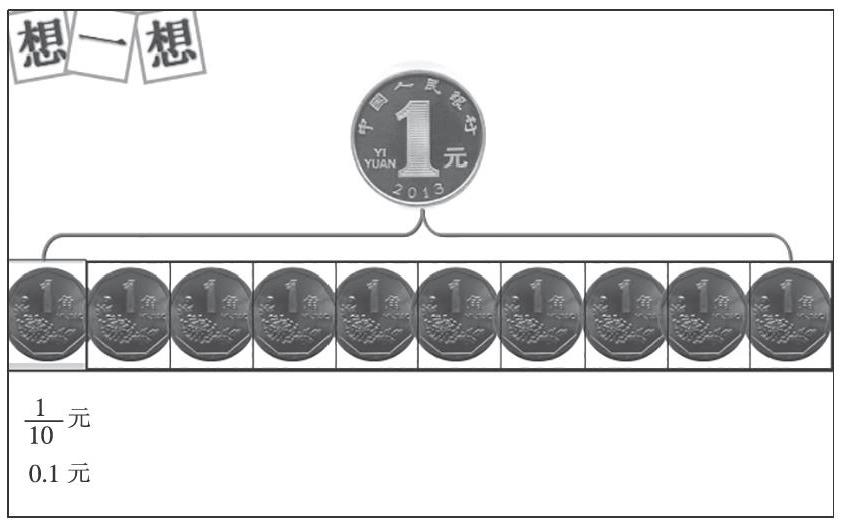
(一)借助1角认识0.1
师:瞧,这是多少?(板书:1角)
师:你还会怎么说?和你的同桌快速交流一下。
(板书:十分之一元)
师:你是怎么想的呢?
师:是呀!把1元平均分成10份,1角就是其中的一份,就是十分之一元。
师:还有人会怎样说呢?(板书:0.1元)你又是怎么想的呢?
师(一边板书一边小结):真了不起!把1元平均分成10份,其中的一份就是1角,用分数表示是十分之一元,也可以写作小数0.1元。
(板书:1角=十分之一元=0.1元)
教师相机介绍小数的读写方法。
对于学生来说,一角硬币是生活中经常接触的,学生几乎也都知道一角可以用0.1元来表示。把1枚1元硬币换成10枚1角硬币并整齐地排列在一起,一方面是让学生深刻感受1角是1元的十分之一,另一方面也为后面直观图的呈现打下基础。教师接着用长方形的框子将10枚1角硬币转化成10个小长方形拼成的长条。这个长条就将学生的思维从实物抽象到图形中来。
(二)自主探究零点几
师:1角是0.1元的话,那2角呢?
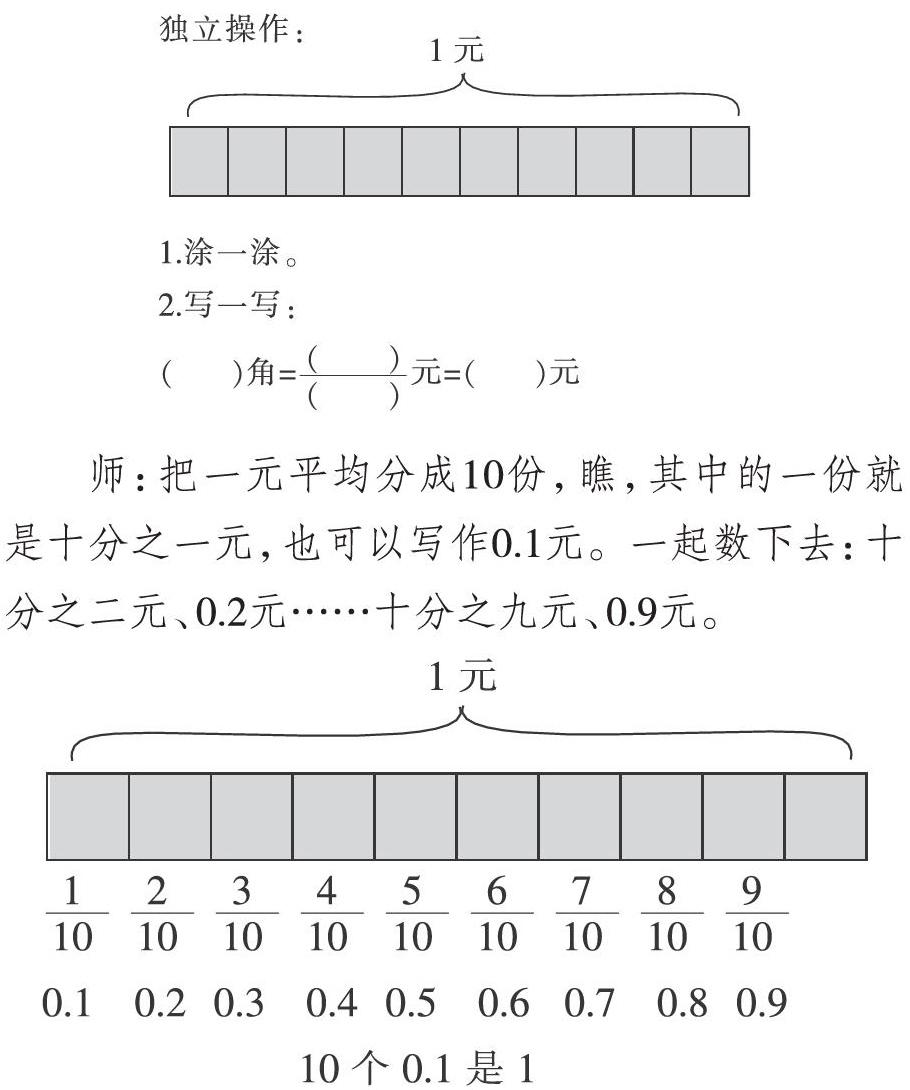
师:同学们,刚才咱们把一元平均分成10份,表示出了0.1元。你還想表示零点几元呢?
师:接下来我们涂一涂,像老师这样写一写,用分数表示是十分之几元,再写成小数。(活动单自主探究一)
师:把一元平均分成10份,瞧,其中的一份就是十分之一元,也可以写作0.1元。一起数下去:十分之二元、0.2元……十分之九元、0.9元。
在这一环节,学生通过独立操作及交流,脱离了具体的元、角之间的铺垫,直接在直观图寻找小数。在这里,学生进一步认识到小数和分数之间的联系。
二、抽象图,借熟悉的模型来理解
(一)借助不同模型来认识
师:刚刚咱们用这个图形表示一元,我把它变一变,你还能找到0.1元吗?这样呢?
除了可以表示1元,用这个图形表示1米行吗?你能找到0.1米吗?(再变)现在呢?
在这里,教师逐渐将长条变形,让学生认识到图形的形状变了也可以表示小数。而长条的不断压缩最终变成类似于数轴的图形,为后面的教学打下基础。同时,不仅图形的形状在变化,这个图形表示的模型也在变,从1元变成1米,让学生在其中寻找小数。教师还要继续追问:除了表示1元、1米,这里的图形还能表示什么呢?引发学生进一步的思考。
(二)通过对比分析来理解
师:为什么图形不同、单位不同,我们都能找到相应的0.1?
师: 是的,不管是1元,1米,还是1什么,把一个图形或一条线段平均分成10份,取其中的几份就是分数十分之几。
通过这个问题的提出,要让学生抽象出分数与小数的本质联系,同样要学生明确:直观图的出现只是为了辅助我们理解一位小数的概念。这样的图形不一定有固定的形式,只要能将它平均分成10份,我们就能找到其中的零点几。也为后面让学生用自己喜欢的方式来表示小数打下基础。
三、数学图,用不同的方式来表示
(一)用喜欢的形式来表示
师:咱们来轻松一下,玩个摸钱的游戏。不过呀,游戏要升级,摸出来的钱请你用小数来表示。
(假设摸出1元2角。展台展示,用小数表示是1.2元)
师:谁来说说这个小数的整数部分和小数部分分别是多少呢?
师:你能用自己喜欢的方式表示出这个小数吗?请你在学习单最下面的方框里画一画。仔细想想,这几个同学的作品有没有共同的地方?
学生的作品主要以上面三种为代表,画图1的学生更多关注在人民币1元2角的实物形象上。表面上看图2和图3的画法几乎一样,但仔细思考,两者也有很大的区别。画图3的学生特意画出了两个完整的正方形,每个正方形表示1元,第二个正方形被平均分成10份,其中的2份用来表示2角。这种表示方法对1.2的表示更加完整,也显示出该位学生的思维更加缜密。不同的表现形式的直观图能反映学生不同的想法和感受。
(二)用规范的数轴来延伸
师:那你能在数轴上找到小数吗?
师:估一估,这里可能是零点几?如果要准确地知道它们的位置应该怎么办?
师:把0至1之间平均分成10份,这是多少?为什么?这里呢?找1.2呢?2.3会在哪一段呢?你有什么感觉?是的,零点几在0和1之间,一点几在1和2之间……
借助在数轴中填数这一环节,让学生扩大对小数的认知范围,体会小数与整数在数轴上的位置关系。同时,让学生感受小数的延伸。
最后教师再介绍小数发展的简史,进一步拓宽学生的视野,把对小数的认识放到一个更为广阔的背景中,让学生感知其来龙去脉,新知学习在儿童头脑中不孤立、不零碎,建立起广泛而丰富的认知联系。
从与学生密切联系的实物,到联系实物的直观图,再到直观图的变形抽象,最后内化为学生自己的图形,本节课的教学离不开图形的引导与辅助。直观图的出现,让学生对知识从认识到理解再到最终内化,使教师的整个教学有了梯度。
数学是一门抽象性和逻辑性很强的学科,而数学概念则是数学的重要组成部分。小学生的思维能力和认知能力还难以直接把握抽象的概念。直观图利用形象的图案和图示来表示数学概念,更加方便学生掌握。因此,在教学中,教师要精心选择合适的、有效的直观图,将它呈现、转化以帮助学生理解,为我们的教学提供便利。

