基于概率优势关系粗糙集的第三方物流供应商选择评价*

□ 钟谨贵，翁世洲，朱 俊

(广西民族师范学院 经济与管理学院,广西 崇左 532200)

1 引言

迄今，经济全球化趋势凸显，我国跨境电商市场发展迅速，随着一系列跨境电商综合试验区的设立，市场规模得到进一步扩大，第三方物流随之迎来更大的发展机遇。大多数企业为了能够在日益激烈的竞争环境中生存并发展下去，将非核心的物流业务外包给更专业、更高效的第三方物流供应商，以此降低物流成本、增强企业核心竞争力。跨境电商企业各方面物流服务需求不断增加，企业选择第三方物流供应商的依据不再局限于价格、时效，而是逐渐趋向于选择综合物流服务能力强的第三方物流供应商。目前，大多数企业仍选用较为传统的选择方法，如依据企业管理层或专业人员的以往经验进行选择，传统的选择方法大多数需要赋予指标权重，主观性均较强。

关于供应商选择评价问题的研究，国内外已有一些相关成果，如国外学者Dickson(1966)[1]是最早对供应商评估指标体系进行研究的学者，通过对170份采购代理和采购管理者的调查实践报告进行研究，提出了23个供应商评价指标。Lee(2009)[2]从利益、机会、成本和风险等角度考虑了供应商评估。Azadeh A等(2016)[3]提出了基于田口法(Taguchi Mcthod)和数据包络分析(Data Envelopment Analysis,DEA)的供应商信用体系模型。Raut等(2017)[4]提出了数据包络分析和人工神经网络结合的一种更准确、更系统、更有效的选择第三方物流供应商的方法，运用数据包络分析法辨别出效率最高的供应商，筛选出不合适的供应商，最后利用人工神经网络进行排序，做出最终选择。国内学者林勇等(2000)[5]提出了对供应商进行评估可以考虑质量、性能、供应商业务能力和环境等指标。李钧(2014)[6]从供应链合作伙伴关系的角度出发，构建企业能力、质量水平、企业信誉、合作程度四个层面的评价指标体系。薛善召(2016)[7]提出了层次分析法和熵权法结合的选择模型，并用实例进行分析，验证了该综合评价模型的有效性。陈欢等(2017)[8]针对企业选择第三方物流供应商时的考虑因素，对50家不同行业的企业进行问卷调查，结果显示企业最关注的四个因素分别为物流服务质量、成本控制、附加增值业务水平、企业财务状况，其中，物流服务质量是企业着重考虑的因素。王鲁萍等(2018)[9]通过构建运营能力、服务质量、成本、发展潜力和绿色水平五个指标的第三方物流供应商选择评价指标体系，提出了一种基于直觉模糊VIKOR和熵权法的供应商选择方法。杨澄懿等(2019)[10]通过风险视角，对军队物资运输过程中可能出现的失效模式进行了研究，运用FMEA法进行选择分析，经检验该方法计算方便、操作简单。

综上所述，国内外大多数学者无论是在评价指标体系方面还是选择评价方法方面的研究均取得了丰硕的成果。尽管评价供应商不再局限于价格、质量、基础设施、合作能力和服务能力等评估指标，选择评价方法也逐渐多样化，但是仍存在一些不足之处，大部分选择方法都要先对指标赋予权重，且主观性过强。因此，本文运用一种不需要确定指标权重、完全依赖原始数据、客观性强、容错率较好的概率优势关系粗糙集选择评价模型[11]，以期更好地解决多属性决策的排序问题，为企业提供更合理有效的选择依据。

2 概率优势关系粗糙集模型[11]

定义1称一个四元集合Z=(U,A,V,f)为一个信息系统，U={x1,x2，…,xn}为有限对象集，A={a1,a2,…,am}为有限条件集，V={v1,v2,…,vk}为条件属性的值域，对象U与条件属性A的关系集可表示为f={fk:U×A→V,k≤m}。

假设每个条件属性的值域两两相互比较具有优势关系，那么称这个信息统统为序信息系统。

定义2设Z=(U,A,V,f)为序信息系统，∀xi,xj∈U，a∈A记作：

(1)

称之为xi与xj的取值在条件属性a下的二值判断，Pa(xi,xj)=1表示在条件属性a下，xi的取值优于或等于xj，Pa(xi,xj)=0则表示在条件属性a下，xi的取值劣于xj。

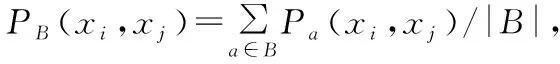
PB=[pB(xi,xj)]n×n

(2)

定义4序信息系统Z=(U,A,V,f)中，Z在B下的概率优势关系可记作：

(3)

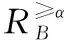
(4)

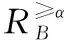
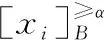
(5)

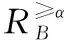
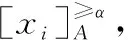
(6)

(7)

3 实证分析

3.1 MY公司简介

MY公司成立于2013年10月30日，坐落于全球最大的小商品集散中心——义乌，义乌被誉为“小商品之都”，是一家专门从事跨境电商出口零售的小型企业。该公司目前主要依托亚马逊北美站电商平台进行网络零售，其主要经营范围为服饰配饰类、美妆个人护理类、玩具类、家具类等。公司共有三个部门，分为运营部、仓管部、物流部。公司规模较小，资金与资源有限，尚未建立自营物流，因此，为了提高公司的核心竞争力专注于核心业务，并提高物流服务质量，将公司的非核心物流业务外包给义乌中小型国际货运代理公司。

3.2 指标与数据

本文通过阅读参考文献[6，8，9]出现频率较高的评价指标，并结合MY公司的实际物流需求，基于客观全面性原则、稳定可比性原则、评价可获取性原则、灵活可操作性原则、目的性原则，构建第三方物流供应商综合物流服务评价指标体系，将MY公司的第三方物流供应商评价指标确定为物流成本(a1)，运输时效(a2)，顾客满意度(a3)，合作紧密程度(a4)，附加增值服务(a5)，报关与清关能力(a6)，企业信誉(a7)，其中a1，a2，a5，a6，a7均为10分制，a3，a4按相应百分比表示，所有指标均为效益型指标，即取值越大越好。

MY公司内部物流人员组成评分小组，根据公司实际物流需求对五家待选供应商各指标进行评分。五家第三方物流供应商分别为：天木(x1)，锦远(x2)，扬翔(x3)，盈和(x4)，汇天(x5)。MY公司用于评价各供应商7个指标分别表示为： MY公司对五家待选家供应商评价指标打分原始数据如表1所示。

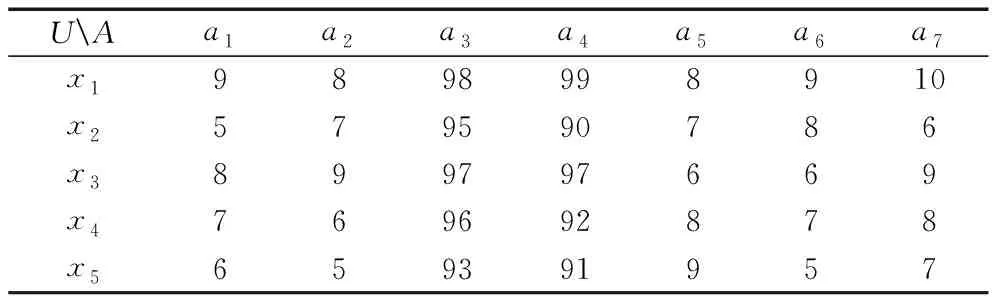
表1 待选供应商选择指标的评分原始数据

3.3 概率优势关系评价模型应用

对五家待选供应商的综合物流服务能力进行排序，按上节中所给步骤计算如下：

①计算出判断矩阵P。依据公式(1)和公式(2)，将各供应商所有评价指标进行两两比较，则计算出的判断矩阵P如下：

②计算出判断矩阵P在不同可信度下α的概率优势矩阵T。依据公式(3)和公式(4)确定截集，分别取α=0.5，α=1，依据公式(7)，计算出概率优势判断矩阵T如下：

③计算出不同可信度α下的各对象的概率优势类。依据公式(5)，得出概率优势关系类如下：

④计算出各个对象的概率优势矩阵。依据公式(6)，将步骤3中的各对象的优势关系类进行两两比较，得出概率优势矩阵如下：

⑤计算出不同可信度下各对象的综合优势度。依据公式(7)，对不同可信度下的概率优势矩阵按行求得各行平均值，得：

在不同可信度下计算出来的概率综合优势度不同，故而得出的排序方案结果可能存在差异。因此，为了综合不同可信度参数下的概率综合优势度值，采用简单平均法进行计算，求出最终的概率综合优势度为：

从中可以看出，x1的概率综合优势度为0.8，x2的概率综合优势度为0.315，x3的概率综合优势度为0.635，x4的概率综合优势度为0.515，x5的概率综合优势度为0.435，五家待选供应商的排名依次为：x1>x3>x4>x5>x2，即天木>扬翔>盈和>汇天>锦远。在五家待选供应商中，天木的概率综合优势度最高，因此MY公司可以优先考虑选择天木作为合作伙伴。从表1原始数据可知，x1之所以可以作为MY公司优先考虑的合作伙伴，主要是因为其各项指标均衡，虽然x1的运输时效和附加增值服务并非最优(排名第二)，但是x1的物流成本、顾客满意度、合作紧密程度、企业信誉、报关与清关能力均排名第一，x1的综合物流服务能力是最强的，因此，MY公司实际的评价结果与概率优势关系粗糙集评价法得出的结果相符，事实证明，概率优势关系粗糙集是一种科学合理且实用的选择评价方法。

4 结束语

本文运用一种不需要确定指标权重、完全依赖原始数据且客观性强的概率优势关系粗糙集选择评价模型，根据MY公司实际物流需求，构建评价指标体系，进行实证分析，验证了该选择评价模型的科学性、合理性。该选择评价模型可以很好地避免因为单个指标评价、人为因素以及感情因素对评价结果的影响，且将此选择评价方法应用于第三方物流供应商选择评价中有一定的新颖性，为各类企业日后进行第三方物流供应商时提供有益的参考借鉴。