局部均布荷载作用下四边支承矩形板的内力计算

杨成永 马文辉 韩薛果 程霖

摘   要：以矩形板的Navier解为基础，采用带补充项的傅里叶级数作为挠度函数，研究了局部均布荷载作用下四边支承矩形薄板的弯曲问题. 推导了确定待定系数的线性代数方程组，给出了简支边和固支边不同组合条件下的统一计算公式. 讨论了带补充项法级数解的收敛速度，并与叠加法级数解及有限元数值解分别进行了精度和计算量的对比. 结果表明，带补充项法的级数解达到收敛的级数项数约为40项. 带补充项法的级数解与叠加法级数解具有同样的求解精度. 有限元解随网格的细分，计算结果逐渐接近级数法解. 级数解法的计算量与有限元解法相比是微不足道的. 研究成果适于进行构筑物顶板受局部均布荷载作用的结构计算.

关键词：矩形板;四边支承;局部均布荷载;级数解;求解精度

中图分类号：U411                           文献标志码：A

Internal Force Calculation of Four Edges Supported Rectangular

Plates under Local Uniformly Distributed Load

YANG Chengyong，MA Wenhui?，HAN Xueguo，CHENG Lin

（School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China）

Abstract：On the basis of Naviers solution to rectangular plates， the bending problem was studied for the four edges supported thin plates under local uniformly distributed load， where the double Fourier series with additional terms was adopted as the deflection function of the plates. Linear algebraic equations for solving the undetermined coefficients were derived. A unified solution was obtained to the rectangular plates with clamped and simply supported edges. The rate of convergence was discussed on the solution of the series method with additional terms. The proposed method was compared both with superposition series method on accuracy， and with finite element numerical method on computational cost. The results show that 40 terms should be employed for a convergence of the series. The method with additional terms shows the same accuracy of solution as superposition series method does. The solution by finite element method gradually approaches that by the series method as the mesh gets finer and finer. In comparison with finite element method， the computational time by the series method is negligible. This work is applicable for structural analysis of the top plates of underground buildings under truck wheel pressure.

Key words：rectangular plate;four supported edges;locally uniformly distributed load;series solution;solution accuracy

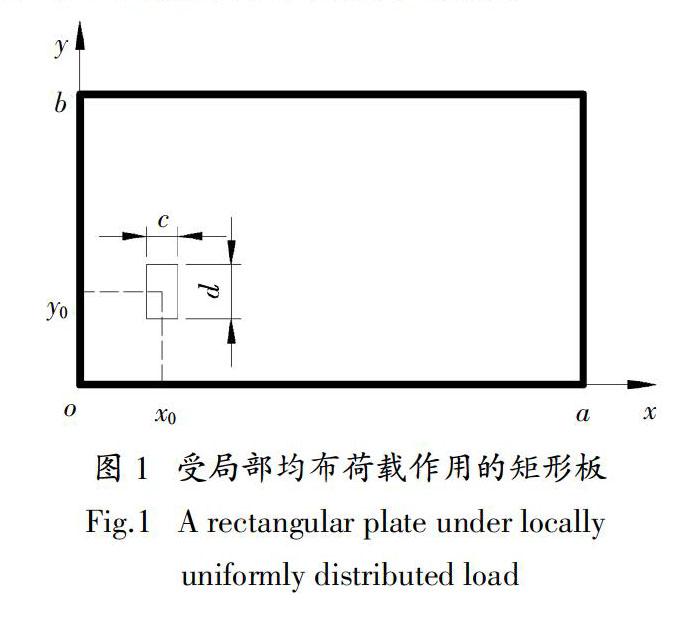
地铁、热力和燃气等地下工程中，地下构筑物的顶板多为四边支承的薄板，板上常承受局部均布荷载如汽车轮压作用. 为了确定像汽车轮压这类荷载在板内产生的最大挠度和内力，需要进行任意位置局部均布荷载作用下挠度和内力的计算.

对四边支承的矩形薄板问题，可以从四边简支板的Navier解出发，采用叠加方法[1-2]或加补充项的方法[3-4]解决. 如：蔡长安等[5-6]以带附加补充项的Fourier级数作为挠度函数，求解了Winkler地基及Pasternak地基上自由边矩形板的弯曲问题. 许琪楼等[7-8]采用一种能满足自由角点条件的挠度表达式，解决了二邻边支承二邻边自由矩形板和二邻边及对角点支承矩形板的弯曲问题. 他们还采用叠加方法[9-10]，提出了四边支承矩形板及一边固定一角点或二角点支承的矩形板的统一求解方法. 岳建勇等[11-12]采用一种双三角级数形式的挠度函数，得到了三边固定一边自由及两对边固定两对边自由矩形板的精确解. 钟阳等[13]在辛几何空间中利用分离变量法推导出了四边固支弹性矩形薄板的精確解析表达式. 于天崇等[14]假定矩形板的抗弯刚度沿板的宽度方向按照一般幂函数形式变化，研究了四边简支一对边受弯作用下面内变刚度矩形板的弯曲问题. 肖闪闪等[15]采用载荷叠加法研究了集中载荷下四边固支正交各向异性矩形板的线性弯曲，并讨论了经典Kirchhoff薄板假设对于集中载荷的适用性.

4.4.2   与文献[16]对比

文献[16]列出了四边简支板中央受局部均布荷载作用时弯矩的计算系数. 为与其对比并避免查表计算中的插值，取泊松比μ = 0，轮压x方向分布长度c = 2 m，y方向分布长度d = 1 m，其余参数采用4.2节的数据，板四边均简支.

根据 =  = 1.4， =  = 0.4， =  = 0.2，按文献[16] 中表4-29查得计算弯矩Mx的系数为0.148 0，My的系数为0.130 8. 然后有

计算结果列于表3.

由表3看出，两种方法的结果，前3位有效数字相同. 由于文献[16]表格的有效数字是4位，可以认为表3中两种结果是一致的.

4.5   计算结果与有限元对比

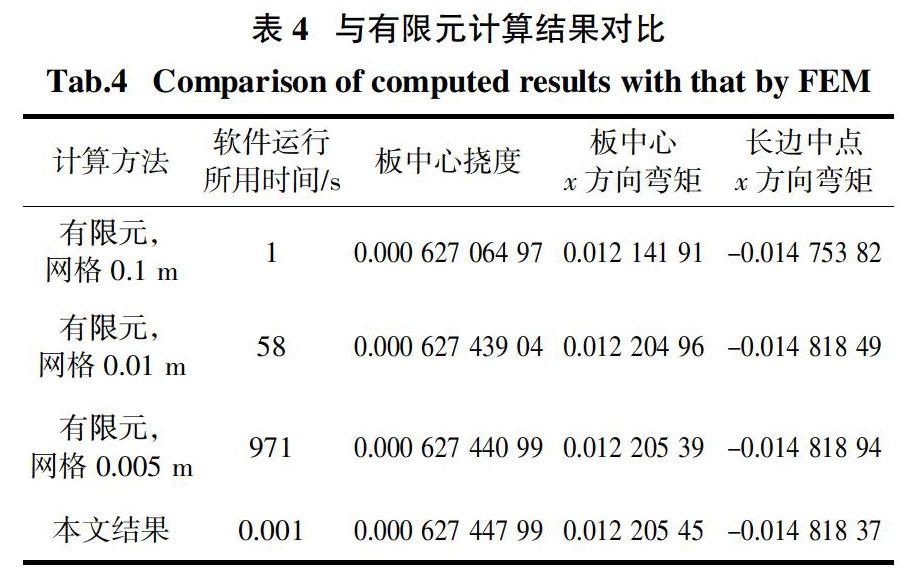
采用4.2节的计算参数，板左边（x = 0边）及前边（y = 0边）固支，其余两边简支. 按相同的参数和边界条件采用ANSYS软件SHELL63号单元，划分3种粗细不同网格进行计算. 计算结果列于表4.

由表4可看出：

1）随有限元网格的加密，计算结果逐渐趋于本文的级数解. 由此可说明，本文级数解是四边支承板变形问题的理论解或精确解. 当有限元网格细到5 mm × 5 mm时，挠度及弯矩有5位有效数字与级数解相同. 可以认为这时数值解与级数解基本一致.

2）表4中的软件运行所用时间是从数据输入到输出全部的计算机运行时间. 要达到较高的精度，有限元需要花费的计算机时间大大高于级数解. 就本算例来说，相差达10万倍以上. 需要注意的是，本算例中，有限元在5 mm × 5 mm网格时，需要求解的方程组的阶数，不少于（x方向节点数5/0.005） × （y方向节点数7/0.005） × 6个自由度 = 840万;而级数解取40项时需要求解的方程组的阶数仅为40 × 2个固支边 = 80.

5   结束语

采用带补充项的挠度函数，研究了四边支承矩形薄板的弯曲问题. 给出了局部均布荷载作用下简支边和固支边不同组合条件下的统一计算公式.

对比计算表明，以Navier解为基础带补充项的傅里叶级数解，达到收敛的级数项数约为40项. 该级数解与其他采用叠加法得到的傅里叶级数解，具有同样的求解精度. 与有限元数值法相比，级数解的计算量十分微小.

值得一提的是，式（3）若换成满布荷载、线荷载和集中力相应的傅里叶系数，本文方法也适用.

参考文献

[1]    TIMOSHENKO S. WOINOSKY-KRIEGER S. Theory of plates and shells [M]. 2nd ed. New York：McGraw-Hill Book Company，Inc，1959：180—228.

[2]    张福范. 弹性薄板[M]. 2版. 北京：科学出版社，1984：58—62.

ZHANG F F. Elastic thin plates [M]. 2nd ed. Beijing：Science Press，1984：58—62. （In Chinese）

[3]    严宗达. 结构力学中的富里叶级数解法[M]. 天津：天津大学出版社，1989：150—197.

YAN Z D. Fourier series solutions in structural mechanics [M]. Tianjin：Tianjin University Press，1989：150—197. （In Chinese）

[4]    杨端生，黄炎. 矩形板结构的弯曲问题[J]. 湖南大学学报（自然科学版），2004，31（6）：65—69.

YANG D S，HUANG Y. The problem of bending of rectangular plate structure [J]. Journal of Hunan University （Natural Sciences），2004，31（6）：65—69. （In Chinese）

[5]    蔡長安，严宗达. Winkler地基上自由边矩形板横向弯曲的Fourier级数解[J]. 贵州工学院学报，1996，25（2）：53—61.

CAI C A，YAN Z D. Fourier series solution for bending problem of the rectangular plates with free edges on Winkler foundation [J]. Journal of Guizhou Institute of Technology，1996，25（2）：53—61. （In Chinese）

[6]    蔡长安. Pasternak地基上自由边矩形板弯曲问题的Fourier级数解[J]. 贵州工业大学学报，1998，27（1）：21—31.

CAI C A. Fourier series solution for bending problem of the rectangular plates with free edges on Pasternak foundation [J]. Journal of Guizhou University of Technology，1998，27（1）：21—31. （In Chinese）

[7]    许琪楼，姬同庚. 二邻边支承其余边自由的矩形板在均布荷载作用下的弯曲解[J]. 土木工程学报，1995，28（3）：32—41.

XU Q L，JI T G. Bending solutions of rectangular plate with two adjacent supported edges and two free edges subjected to uniform load [J]. China Civil Engineering Journal， 1995， 28（3）： 32—41. （In Chinese）

[8]    许琪楼，姜锐，唐国明. 二邻边支承二邻边自由的矩形板弯曲统一求解方法[J]. 东南大学学报（自然科学版），2000，30（2）：138—142.

XU Q L，JIANG R，TANG G M. Unified solution method of rectangular plate bending with two adjacent supported edges and two free edges [J]. Journal of Southeast University （Natural Science Edition），2000，30（2）：138—142. （In Chinese）

[9]    许琪楼，姜锐，唐国明，等. 四边支承矩形板弯曲统一求解方法——兼论纳维叶解与李维解法的统一性[J]. 工程力学，1999，16（3）：90—99.

XU Q L，JIANG R，TANG G M，et al. Unified solution method on rectangular plate bending with four edges supported [J]. Engineering Mechanics，1999，16（3）：90—99. （In Chinese）

[10]  许琪楼，姜锐，唐国明，等. 一边固定一角点或二角点支承的矩形板弯曲统一求解方法[J]. 计算力学学报，1999，16（2）：210—215.

XU Q L，JIANG R，TANG G M，et al. Unified solution method on rectangular plate bending with one edge built-in and one or two corner point supported [J]. Chinese Journal of Computational Mechanics，1999，16（2）：210—215. （In Chinese）

[11]  岳建勇，曲慶璋. 三边固定一边自由矩形板的精确解[J]. 青岛建筑工程学院学报，1999，20（1）：16—21.

YUE J Y，QU Q Z. The precise solution of rectangular plate with three edges built in and the fourth edge free [J]. Journal of Qingdao Institute of Architecture and Engineering，1999，20（1）：16—21. （In Chinese）

[12]  岳建勇，曲庆璋. 两对边固定两对边自由矩形板的精确解[J]. 青岛建筑工程学院学报，2000，21（2）：12—17.

YUE J Y，QU Q Z. Exact solution of rectangular thin plate with two opposite edges clamped and the other two edges free [J]. Journal of Qingdao Institute of Architecture and Engineering，2000，21（2）：12—17. （In Chinese）

[13]  钟阳，李锐，刘月梅. 四边固支矩形弹性薄板的精确解析解[J]. 力学季刊，2009，30（2）：297—303.

ZHONG Y，LI R，LIU Y M. Exact analytic solution of rectangular thin plate with four edges clamped [J]. Chinese Quarterly of Mechanics，2009，30（2）：297—303. （In Chinese）

[14]  于天崇，聂国隽，仲政. 变刚度矩形板弯曲问题的Levy解[J]. 力学季刊，2012，33（1）：53—59.

YU T C，NIE G J，ZHONG Z. Levy-type solution for the bending of rectangular plates with variable stiffness [J]. Chinese Quarterly of Mechanics，2012，33（1）：53—59. （In Chinese）

[15]  肖闪闪，陈普会. 集中载荷下四边固支正交各向异性矩形板的线性弯曲问题[J]. 工程力学，2015，32（6）：28—32.

XIAO S S，CHEN P H. Analytical solutions for bending of clamped orthotropic rectangular plates under a concentrated force[J]. Engineering Mechanics，2015，32（6）：28—32. （In Chinese）

[16]  《建筑结构静力计算手册》编写组. 建筑结构静力计算手册[M]. 北京：中国建筑工业出版社，1998：227—228.

Working Group of Handbook of Building Structural Statics. Handbook of building structural statics[M]. Beijing：China Architecture & Building Press，1998：227—228. （In Chinese）